GPS/INS紧耦合导航中多路径效应改正算法及应用

（1. 中国矿业大学 国土环境与灾害监测国家地理信息局重点实验室，徐州 221116；2. 中国矿业大学 环境与测绘学院，徐州 221116）

（1. 中国矿业大学 国土环境与灾害监测国家地理信息局重点实验室，徐州 221116；2. 中国矿业大学 环境与测绘学院，徐州 221116）

针对GPS伪距观测值受多路径误差影响较大，限制了GPS/INS紧耦合导航中导航精度提高的问题，在传统静态多路径消除方法的基础上，提出了导航过程中多路径效应动态消除算法，并应用于GPS/INS紧耦合导航。首先给出了GPS/INS紧耦合导航的动力学模型和观测模型以及静态定位多路径消除的方法，通过频谱分析探究了非差观测值序列的特殊性，引入了移动窗口提取动态导航过程非差伪距观测值的多路径，最后利用实测数据验证了算法的有效性。结果表明：对比没有经过多路径改正的组合导航算法，基于伪距多路径改正的GPS/INS紧耦合导航增强了滤波融合观测值的精度，减少了多路径效应对于伪距观测值的影响，平衡了伪距观测值和多普勒观测值的权重，提高了GPS/INS紧耦合导航的直接可测参数（位置、速度）和间接可测参数（姿态）的精度，北向、东向和高程三个方向的位置误差分别减小了18.8%、25.7%，和1.5%。

紧耦合导航；多路径；伪距；移动窗口

全球定位系统(GPS)和惯性导航系统(INS)的观测方法和观测数据均具有良好的互补性[1]，将两者组合起来可以高效发挥两个系统各自的优点，通过信息融合技术实现高采样率、误差补偿以及丰富的观测值，目前已在导航、测量等领域得到了广泛的应用。

GPS/INS紧耦合导航在卫星个数小于4颗的情况下仍能够为组合导航数据融合提供观测值（伪距和多普勒），有效实时地修正 INS误差项，因此在城市等半遮蔽区域具有很大的优势。在卫星遮挡严重的情况下，紧耦合导航过程中可能只有2颗卫星的观测值参与计算，因此每颗卫星的伪距和多普勒观测值精度对于紧耦合导航效果影响较大。相对于多普勒观测值，伪距观测值精度较低，尤其是伪距观测值受到多路径效应的影响较大。在利用 GPS进行长期监测的过程中，可以根据多路径误差隔天相关性进行多路径误差的削弱[1]。Chan W S利用加速度计和GPS接收机进行组合[2]，减小多路径误差的影响，进行建筑物的变形监测工作。Yedukondalu K利用传统的数字滤波的方法，结合频谱分析对静态条件的多路径误差进行消除[3]。通过对大量静态观测值的分析可以寻求多路径误差的规律[4-5]，从而寻找合适的方法进行消除，取得了一定的效果，但是GPS/INS组合导航对实时性要求较高，上述削弱方法在应用于动态导航的多路径误差消除的过程中存在很大局限性。

本文在研究多路径频谱特性的基础上，利用移动窗口削弱了非差观测值UPD对于多路径消除的影响，提出了动态非差多路径的消除方法，利用消除多路径误差的伪距观测值进行GPS/INS紧耦合导航，并将该算法与未经多路径消除的组合导航算法进行了对比。

1 GPS/INS紧耦合导航模型

1.1 动力学模型

GPS/INS组合导航的动力学模型的构建基于INS误差方程[6]：

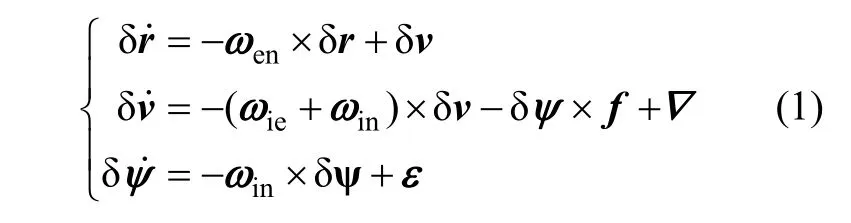
式中，δr、δv和δψ分别是位置、速度和方向误差向量，ωen是地理坐标系相对于地球坐标系的旋转角速度矢量，ωie是地理坐标系相对于惯性坐标系的旋转角速度矢量，ωin是地理坐标系相对于惯性坐标系的旋转角速度矢量，f是加速度计测量的比力矢量。加速度误差向量▽和陀螺误差向量ε近似于随机游走过程模型，其模型表达式为：

式中， u▽和 uε是高斯白噪声向量。

只利用单台GPS接收机的观测信息进行组合导航，接收机的钟差不能通过双差的方式来消除，所以动力学模型中包括GPS接收机的钟偏和钟漂的误差：

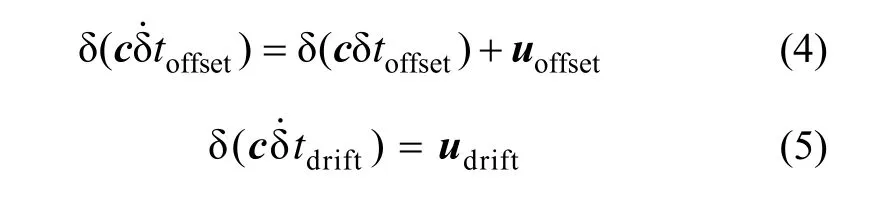
综合以上各式，INS误差方程表达式为[7]

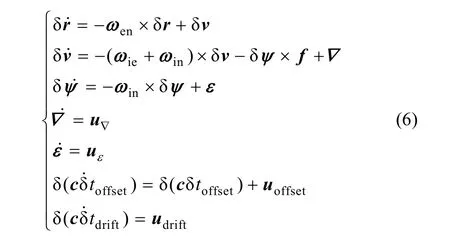
写成矩阵形式为：

式中，F为系统状态转移矩阵，X为误差状态向量，

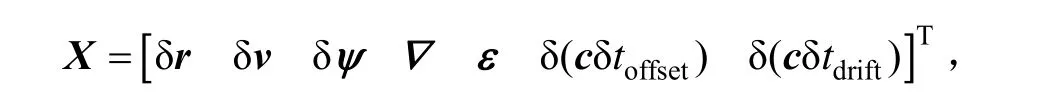
u 为状态过程噪声向量。

1.2 观测模型

将加入改正的 GPS伪距和多普勒观测值与利用INS输出的位置和速度计算的伪距和伪距率作差构造紧耦合观测值：

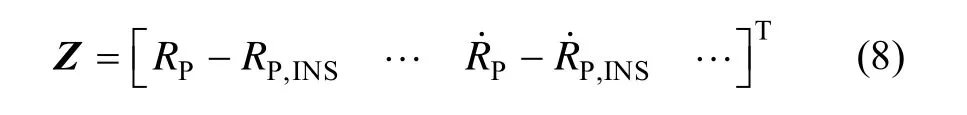
式中， RP为加入了各项改正的 GPS伪距观测值，RP,INS为利用 INS解算的载体位置和卫星位置反算的伪距值，为利用多普勒观测值计算的接收机伪距变化率，为利用INS解算的载体速度和卫星速度反算的伪距变化率。其中[8]

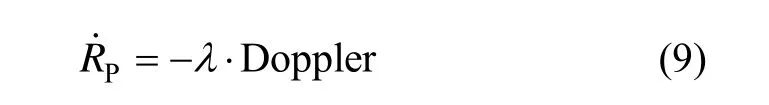
式中，Doppler为接收机的多普勒观测值，λ为多普勒观测值的载波波长。

则Kalman的量测方程为[9]：

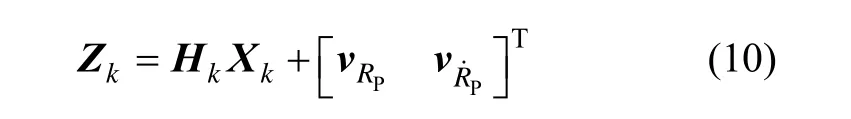
式中： Hk为观测矩阵；νRP和 νR˙P,INS分别为伪距和伪距率的观测噪声，满足高斯白噪声特性。

2 多路径消除

2.1 差分定位多路径消除

在GPS定位或基线解算中，认为多路径与观测噪声同时包含在残差中。对于C/A码而言，多路径的影响可达到10～20 m，最严重时可达到100 m；对于P码的影响最大可达到10 m左右。相比较而言，多径对载波的影响较小，最大影响为1/4波长，一般情况下，其影响约为1 cm左右。因此，可以利用模糊度固定的载波解算伪距多路径效应。载波非差定位模型联立可得到伪距多路径[10]：

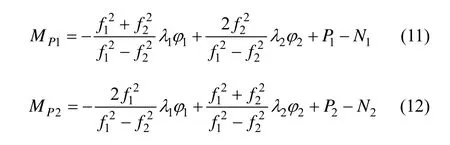
式中：P为伪距观测值，φ为载波相位观测值；MP1和MP2为两个伪距的多路径效应；f1和f2为载波相位的频率，N1和 N2为两个组合的模糊度。对于同一个卫星，在连续观测并且不存在周跳的情况下，模糊度参数不会变化，尤其是对于短基线的双差解算，模糊度参数不会受到未校准的相位延迟(UPD)的影响。因此，通过多历元的MP+N序列(简写为S序列)取平均的方式估计模糊度参数N，然后将各历元的S序列减去这一均值得出伪距多路径效应。

上述多路径去除方法是通过提取S序列的趋势项来解算每个历元的多路径误差，该方法是建立在模糊度参数不会变化以及多路径误差满足高斯特性的两个假设之上，而且由于多路径误差和接收机所处环境关系密切，难以准确建立统一的模型，因此认为多路径误差满足高斯特性是可以接受的。对于双差解算模式，GPS的模糊度参数变化较小，因此，模糊度参数与具有高斯特性的多路径参数之和的时间序列也具有高斯特性；但是对于非差GPS测量，由于模糊度中的UPD误差不能消除，并且变化具有较大波动性，所以模糊度参数变化明显，上述方法难以发挥效果。

2.2 非差定位多路径消除

由于非差整周模糊度中UPD的存在[11]，非差S序列不满足高斯特性，而整体呈现趋势性，如图 1所示。

可以看出，相对于小幅度的高频动态部分，序列存在明显的低频趋势项误差，说明了模糊度N不再同双差解中具有高斯特性，受到了低频误差的扰动。后处理的方式过程中，GPS静态观测数据的多路径误差的估计可以根据多路径误差的高斯特性，利用小波变换等方法提取S序列的高频动态部分认为是多路径误差，如图2所示。

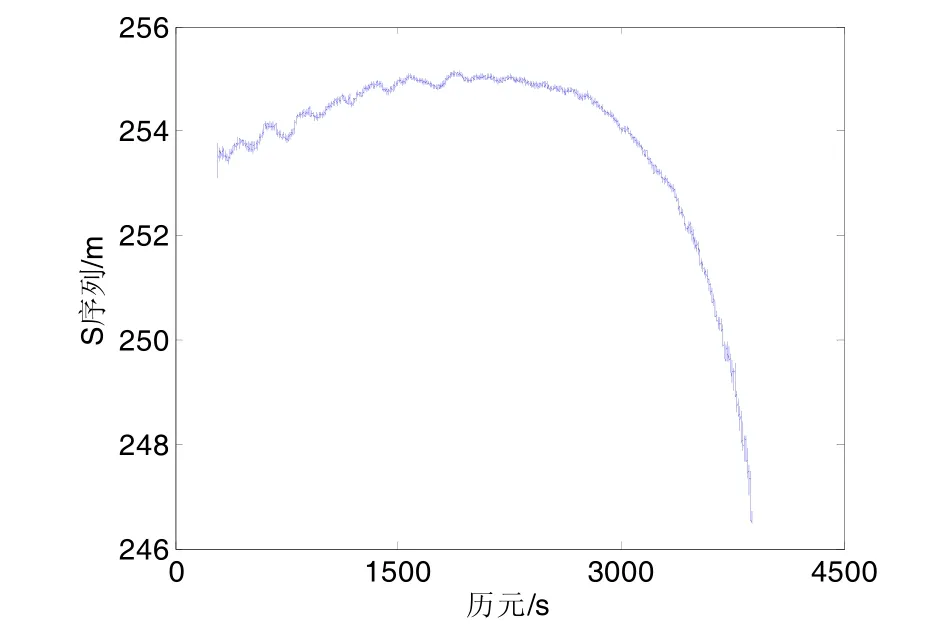
图1 非差S序列Fig.1 Time series of S

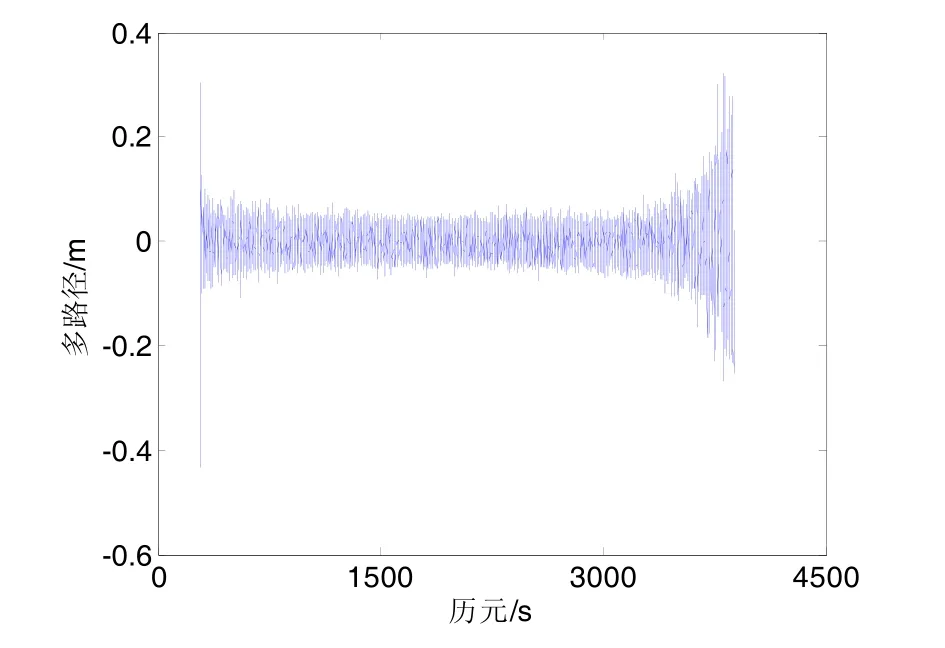
图2 多路径误差Fig.2 Multipath error

为进一步说明非差 S序列的特性，分别对 S和MP序列进行频谱分析，如果N值是没有变化的，S序列和MP序列的频谱分析结果是近似的。

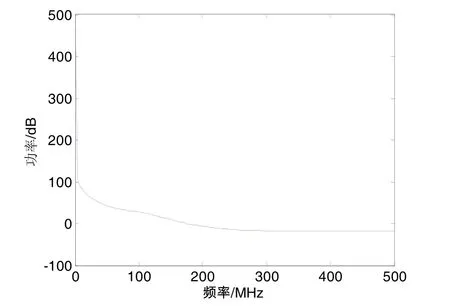
图3 S序列的频谱分析图Fig.3 Spectral analysis of S series

图3为非差观测值S序列的频谱分析图，频率为0时，功率最大，远高于其它频率的功率，说明S序列不具有明显的频率特性。图4分别为图3序列去除0值点的S序列频谱图和图2的MP序列的频谱图， 可以看出，S序列和MP序列的频谱分析结果相差很大。MP时间序列的高频部分的功率较大，符合多路径误差的高斯特性；S序列的低频部分功率大于高频部分，说明了S序列的存在明显的低频趋势项。

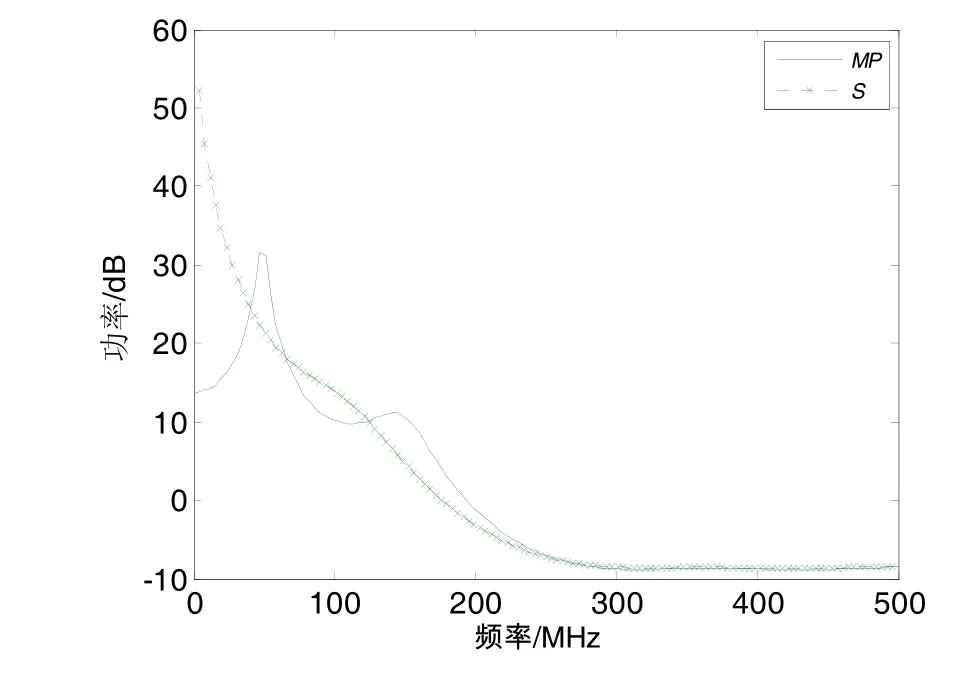
图4 频谱分析对比图Fig.4 Comparison of Spectral analysis

通过上述分析可以看出，对于非差GPS定位，利用时间序列求取平均值的方法不能消除模糊度参数的UPD的影响，因此采用传统方法不能准确估计多路径误差，估计的误差中会引入UPD干扰。

虽然建立在多路径误差满足高斯特性的基础上，通过对非差观测值高动态项的提取可以估计多路径误差，但是高动态项的提取建立在对多数据样本的频率域分析，因此不适合动态导航。

3 GPS/INS紧耦合导航中多路径改正

3.1 动态导航多路径消除

动态多路径的消除要求实时性，所以不能采用简单的提取高频动态噪声的方法。与此同时，GPS/INS紧耦合采用非差GPS观测值，采用传统的序列平均的方法不能消除整周模糊度的UPD的影响。但是，UPD在较短的时间内具有一定的稳定性，可以近似认为具有高斯特性，因此可以引入移动窗口的方式，采用区间序列取平均的方式消除UPD的影响。

动态多路径消除的主要流程(图5)：

① 获取当前历元i的伪距观测值；

② 计算i历元之前的i-n～i-1个历元个MP+N时间序列S (n赋初值100)；

③ 统计计算S时间序列的方差var；

④ 如果var＜0.01，说明S序列近似满足高斯特性，计算S序列的平均值为整周模糊度，计算当前历元的多路径效应；

⑤ 如果var＜0.01，n=n-10；重复上述步骤，当n≤50时，停止计算，不对当前历元的多路径进行改正。

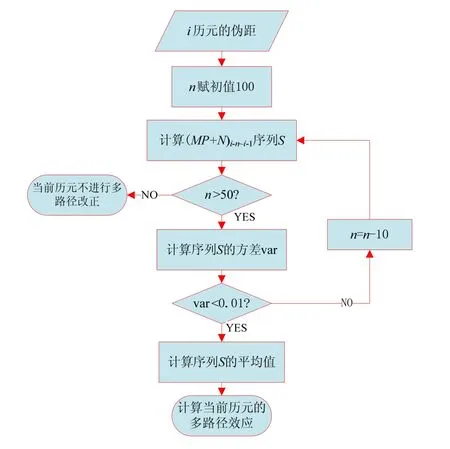
图5 多路径消除Fig.5 Flowchart of multipath correction

3.2 基于多路径改正的紧耦合导航

传统的GPS/INS紧耦合导航系统中只用到了伪距和伪距率观测值，本文由于需要对伪距观测值中的多路径进行改正，所以载波相位观测值也被使用，提高了GPS输出观测值的使用效率。进行多路径改正后的伪距观测值和伪距率观测值一同输出到 Kalman滤波器，与INS输出的位置和速度预测计算的伪距和伪距率组成紧耦合观测值，对紧耦合中的INS和GPS的状态值进行融合滤波修正。组合导航系统状态误差向量反馈到INS力学编排中，对INS状态进行实时校正，实现闭环反馈(图5)。

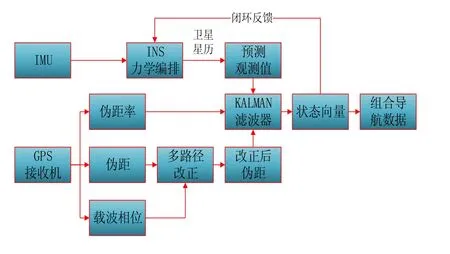
图6 基于多路径改正的紧耦合导航Fig.6 Tightly-coupled navigation with multipath correction

4 实例分析

为验证本文提出的动态多路径消除方法的有效性，进行了车载实测实验。实验数据采集于中国矿业大学南湖校区和云龙湖景区。实验采用 2台LAICA-GPS接收机和1台惯性测量系统，1台GPS接收机作为静止参考基站，另1台GPS接收机和惯性测量系统一起安置在运动车辆内(GPS天线安装在车顶)。实验采用 SPAN-CPT惯性导航系统，表 1是SPAN-CPT惯性导航系统的性能参数。INS数据采集频率为100 Hz，GPS数据采样周期为1 s。数据融合滤波北东地三个方向的位置初始标准差分别为 0.5 m、0.5 m、2 m；速度初始标准差为0.01 m/s、0.01 m/s、0.05 m/s；姿态的初始标准差为 0.01°、0.01°、0.1°；加速度计的零偏为20 mg；陀螺仪的零偏为1 (°)/h。

表1 SPAN-CPT技术参数Tab.1 SPAN-CPT technical parameters

图7为分别利用本文方法对多路径误差的实时结算结果。与图2相比，两种解算方法估计的多路径误差相接近，说明本文提出的动态多路径提取方法和通过后处理提取高频动态噪声方法效果相同。

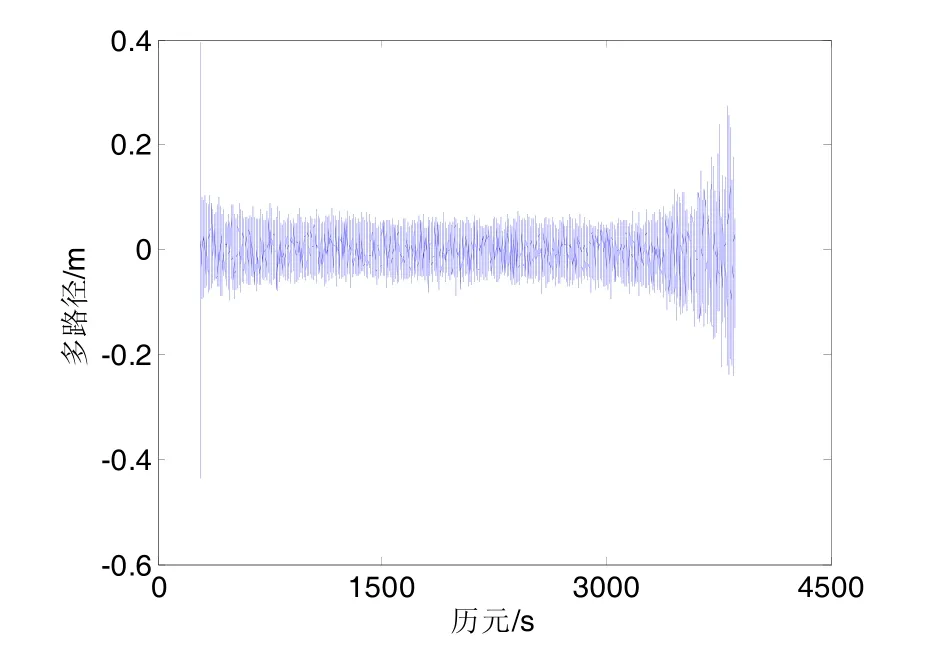
图7 多路径误差Fig.7 Multipath errors

为了说明动态多路径改正对于GPS/INS组合导航的影响，分别利用多路径误差改正前(方案1)和改正后(方案2)两种算法进行组合导航解算并进行比较。图8为两种方案和RTK参考值的平面轨迹图，通过放大后的效果图可以看出，多路径改正后的导航解的平面轨迹更接近于参考值，说明了多路径改正能够有效提高平面位置精度的提高。

图9(a)～图9(c)为两个解算方案在北向、东向和高程三个方向的位置误差序列图，其中两台接收机双差解算的RTK值作为参考值。由于位置误差较小，从经纬度误差角度不便于观察，因此把位置误差转换到北东地坐标系中。从整个实验过程来看，多路径改正后的方案2的三个方向的位置误差明显小于方案1，尤其是北方向和东方向的位置误差分别减小了 18.8%和25.7%；对于高程方向的作用效果较小，位置误差减小了1.5%。这说明通过多路径误差的改正有效地减小了伪距观测值的误差，改善了紧耦合导航输入值的精度，从而提高了位置解算值的精度。

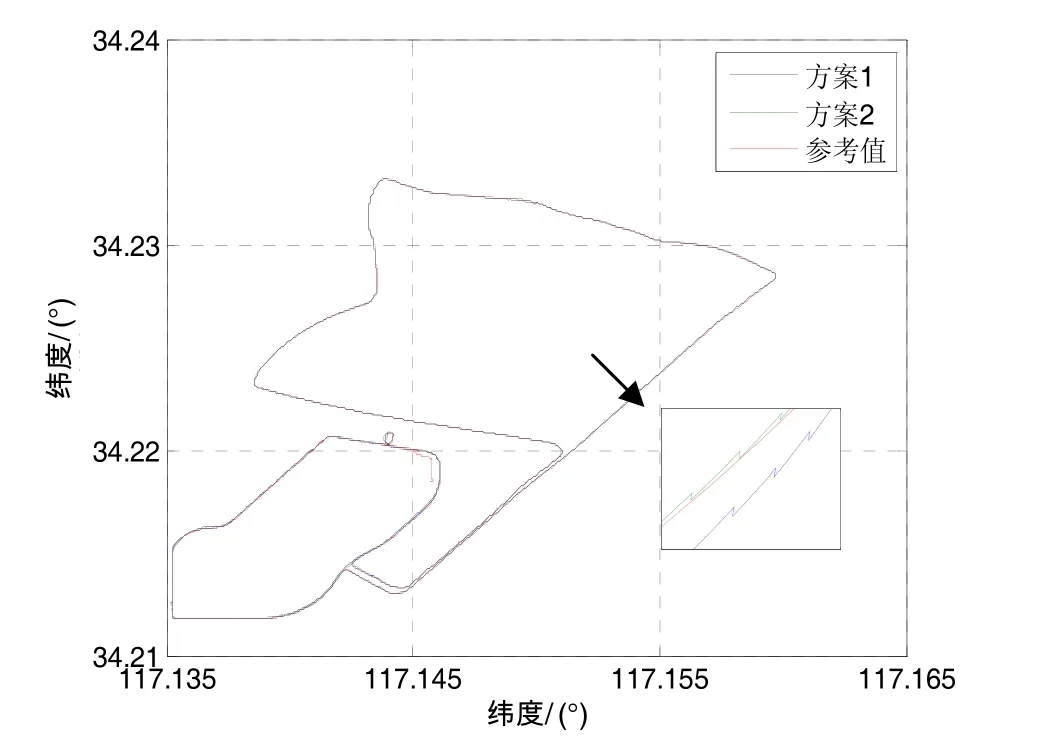
图8 轨迹比较Fig.8 Trajectories of the two schemes

在GPS解算过程中，位置信息通过伪距观测值直接可以得到，因此可以预见，通过改正多路径误差可以提高伪距观测值精度，从而得到更加精确的位置信息。为进一步说明多路径改正对紧耦合的影响，对间接可测参数进行了对比。图9(d)给出了两种解算方案的航向角误差，GPS双差观测值和INS原始观测值通过Waypoint软件后处理得到的姿态作为航向角参考值。可以看出，改正GPS/INS紧耦合导航的多路径误差不但提高了直接可测参数的精度，而且提高了间接可测参数(航向角)的估计精度。从均方差角度分析可以看出，相对于方案1(0.897°)，方案2的航向角误差降低了31.0%(0.619°)。

5 结 论

多路径误差是限制GPS/INS紧耦合导航精度提高的一个重要因素。根据传统的多路径提取动态趋势项的特点，引入移动窗口提取动态非差伪距观测值的多路径，并应用于GPS/INS紧耦合导航。车载试验证明，基于多路径改正的GPS/INS紧耦合导航能够有效削弱多路径效应的影响，增强伪距观测值的精度，提高整个组合导航的位置和姿态精度。

需要指出的是，紧耦合导航的多普勒观测值是利用载波相位时间差分获取的，其也受到多路径误差的影响，因此如何削弱紧耦合导航多普勒观测值的多路径误差的影响是下一步研究的重点。

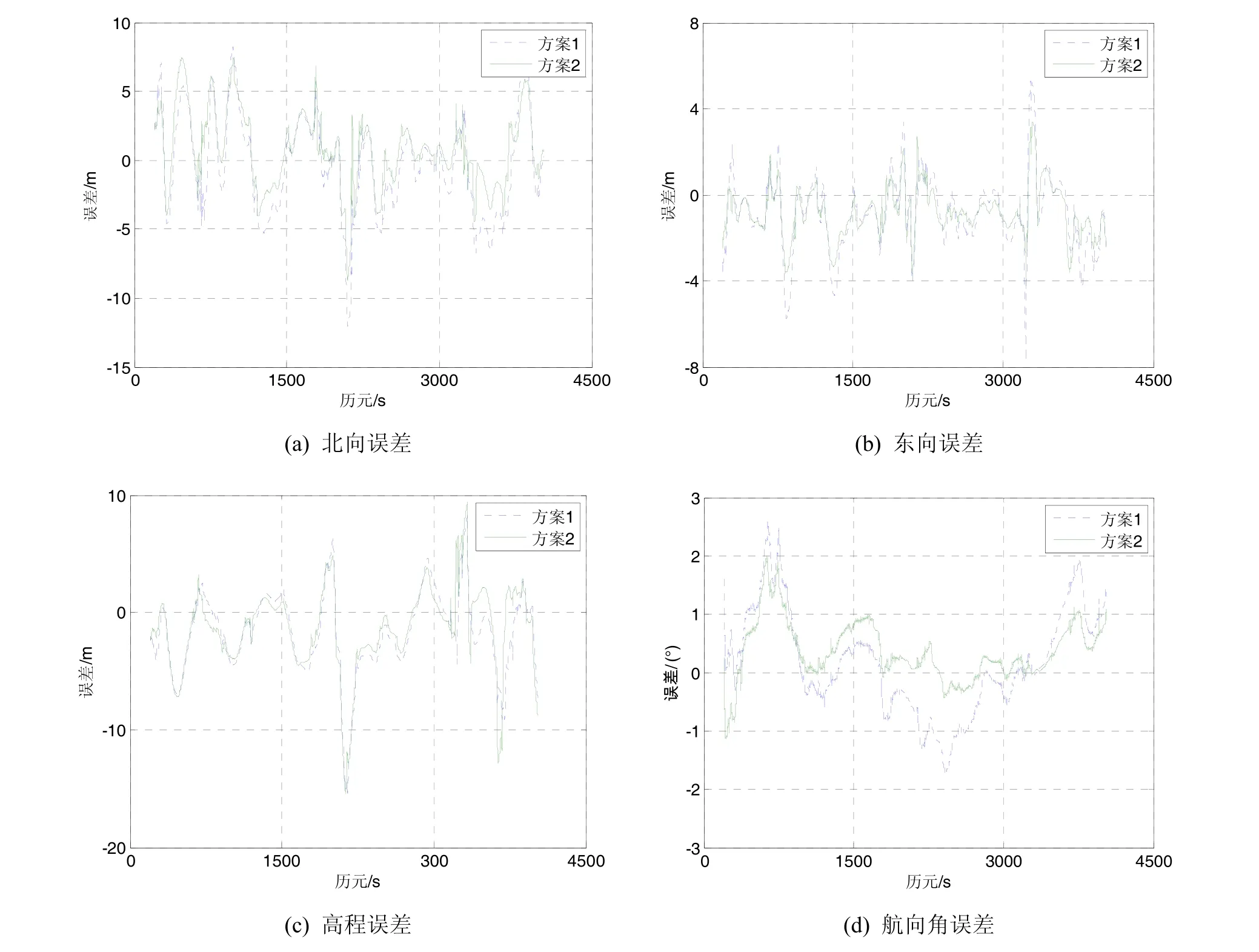
图9 不同方案误差对比Fig.9 Comparison on errors of different schemes

（References）：

[1] Roberts G W, Meng X, Dodson A H, et al. Multipath mitigation for bridge deformation monitoring[J]. Journal of Global Positioning System, 2002, 1(1): 25-33.

[2] Chan W S, Xu Y L, Ding X L, et al. An integrated GPS-accelerometer data processing technique for structural deformation monitoring[J]. Journal of Geodesy, 2006, 80(12): 705-719.

[3] Yedukondalu K, Sarma A D, Ashwani K, et al. Spectral analysis and mitigation of GPS multipath error using digital filtering for static applications[J]. IETE Journal of Research, 2013, 59(2): 156-166.

[4] 刘超，王坚，胡洪，等. 动态变形监测多路径实时修正模型研究[J]. 武汉大学学报(信息科学版)，2010，35(4)：481-485.

LIU Chao, WANG Jian, HU Hong, et al. Research on real time correcting model of multipath in GPS dynamic deformation monitoring[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4): 481-485.

[5] 宋超，李景森，皮寿熹. GPS局域增强系统基准站多路径抑制消除技术[J]. 中国惯性技术学报，2010，18(2)：204-208.

SONG Chao, LI Jing-seng, PI Shou-xi. Technique of multipath-free to GPS local area augmentation system[J]. Journal of Chinese Inertial Technology, 2010, 18(2): 204-208.

[6] Titterton H D, Weston L J. Strapdown inertial navigation technology second edition[M]. Lexington, Massachusetts: MIT Lincoln Laboratory, 2004.

[7] Farrell A J. Aided navigation: GPS with high rate sensors[M]. New York: McGraw-Hill, 2008.

[8] Antonio A. GNSS/INS integration methods[D]. Calgary, Canada: Department of Geomatics Engineering, The University of Calgary, 2010.

[9] YANG Shu-jie, YANG Gong-liu, SHAN You-dong, et al. SINS/CNS tightly integrated navigation algorithm for aerospace vehicles[J]. Journal of Chinese Inertial Technology, 2013, 21(4): 478-483.

[10] 张小红，丁乐乐. 北斗二代观测值质量分析及随机模型精化[J]. 武汉大学学报• 信息科学版，2013，38(7)：832-836.

ZHANG Xiao-hong, DING le-le. Quality analysis of the second generation compass observables and stochastic model refining[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 832-836.

[11] Ge M, Gendt G, Rothacher M, et al. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations[J]. Journal of Geodesy, 2008, 82 (7): 389-399.

GPS/INS紧耦合导航中多路径效应改正算法及应用

李增科1,2，高井祥1,2，姚一飞1，王 坚1,2

GPS/INS tightly-coupled navigation with multipath correction algorithm

LI Zengke1,2, GAO Jingxiang1,2, YAO Yifei1, WANG Jian1,2
(1. NASG Key Laboratory for Land Environment and Disaster Monitoring, China University of Mining and Technology, Xuzhou 221116, China; 2. School of Environment Science and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China)

In GPS/INS tightly-coupled navigation, the multipath error has significant influence on GPS pseudo-range observation and thus limits the navigation precision. Based on classical static multipath correction method, a dynamic multipath correction method was proposed and applied into the GPS/INS navigation. Firstly, the design formulas of observation model and dynamical model were presented in GPS/INS tightly-coupled navigation, and the classical multipath correction method was introduced. Then the characteristic un-differenced observation series is introduced by spectral analysis. A move-window was used to extract the multipath in pseudo-range observation for dynamic navigation. Finally, an actual calculation was performed to test the validity of new algorithm. The results of the experiment indicate that, compared with the integrated navigation without multipath correction, the GPS/INS tightly-coupled navigation based on multipath correction of pseudo-range improves the observation precision of filter fusion and reduce the effect of multipath on pseudo-range observation. The new method balances the weight of pseudo-range observation and Doppler observation. The precision of directly measurable parameters (position and velocity) and indirectly measurable parameters (attitude) in GPS/INS tightly-coupled navigation is improved. The position errors in north, east and height directions are decreased by 18.8%, 25.7% and 1.5%, respectively.

tightly-coupled navigation; multipath; pseudo-range; move-window

联 系 人：高井祥（1960—），男，教授，博士生导师，从事GNSS理论与应用研究。E-mail：jxgao@cumt.edu.cn

1005-6734(2014)06-0782-06

10.13695/j.cnki.12-1222/o3.2014.06.015

P228.4

A

2014-07-03；

2014-11-19

国家863高技术研究发展计划（2013AA12A201）；江苏省普通高校研究生科研创新计划项目（CXZZ12_0939）；江苏高校优势学科建设工程项目（SZBF2011-6-B35）；新世纪优秀人才支持计划（NCET-13-1019）

李增科（1988—），男，博士研究生，从事GPS/INS组合导航研究。E-mail：zengkeli@yeah.net