天然裂缝影响下的复杂压裂裂缝网络模拟
赵金洲 李勇明 王松 江有适 张烈辉
“油气藏地质及开发工程”国家重点实验室·西南石油大学
常规水力压裂裂缝模拟,一般是假设均质地层中不考虑天然缝存在,井眼两侧形成垂直于最小主应力方向的对称双翼平面缝[1]。但从直接的矿井压裂测试[2]到间接的微地震监测[3],都表明在天然裂缝发育的页岩气储层,会形成不对称、不规则的复杂裂缝网络。
开启和扩展天然裂缝是形成缝网的基础。众多学者通过实验和理论分析,研究了人工裂缝与天然缝相交后的物理现象,并建立了裂缝延伸的判定准则[4-5];Warpinski[6]采用线摩擦理论考虑作用在裂缝面的剪应力引起的剪切滑移破坏,并以摩尔库伦准则分析作用在裂缝面的正应力引起的张性破坏。Beugelsdijk等[7]通过实验分析了水平应力差、排量和黏度对分支缝延伸的影响。研究表明,与天然缝相交后形成的裂缝网络复杂程度不仅与地应力相关,而且受到岩石力学参数、天然缝参数、压裂施工参数以及工作液物性所影响[8-10]。
压裂过程中人工缝与天然缝相交后,分支缝的起裂与延伸机理对形成复杂裂缝网络的几何尺寸和复杂程度有重要影响。笔者以断裂力学理论为基础,引入起裂与延伸判定计算准则;在此基础上,考虑附加应力场影响,建立页岩气压裂复杂裂缝网络模型,在求解过程中以等压力梯度值划分裂缝延伸方向上的计算节点,将节点压力作为关键变量显式求解裂缝网络几何尺寸参数;并将起裂与延伸准则作为分支缝扩展依据,避免常规拟三维裂缝模拟中对缝长延伸的复杂拟合过程。与线网模型[11],该模型能够充分考虑储层中任意分布的天然缝对整个裂缝网络结构的影响,井眼两侧的缝网整体形态是非对称且内部的分支缝非均匀间距,更符合微地震测试结果。与非常规裂缝模型相比[12],建立的起裂与延伸判断准则时考虑了剪应力与正应力共同作用下的裂缝尖端周向应力,能够合理解释延伸过程中裂缝转向的物理现象并能计算分支缝扩展延伸中的角度变化;并且通过改进数值求解方法能有效提高计算速度。
1 裂缝起裂与延伸条件分析
1.1 剪应力产生的应力强度因子
在地应力作用下椭圆形天然缝表面的剪应力所产生的Ⅱ型应力强度因子为:

式中K(κ)和E(κ)分别为第一、二类椭圆完整积分;τ为剪应力,MPa;υ为泊松比;ω为剪应力方向与椭圆长轴夹角;θ为椭圆裂缝边缘任意点与长轴夹角;a和b分别为裂缝长、短半轴长度,m。
1.2 正应力产生的应力强度因子
在水力裂缝延伸过程中,不断扩展的裂缝长度和缝内压力重新分布将导致由正应力引起的裂缝尖端应力强度因子动态变化。根据初始起裂位置沿着裂缝延伸方向上按照等压力梯度划分节点,再使用叠加原理得到在不同节点压力作用下的裂缝尖端应力强度因子的值。压力节点划分如图1所示。

图1 裂缝压力节点划分图
由不同节点压力所形成的应力强度因子为[13]:

式中l(i)为第i个压力节点与初始位置的间距;l为人工裂缝长度;pnet(i)为第i个节点处净压力。
在此基础上可得到正应力作用下的Ⅰ型应力强度因子为:

式中n为划分的压力节点总数。
1.3 附加应力场
多条分支裂缝在延伸的同时,相互之间会受到作用在临近裂缝的正、剪应力影响,而形成附加应力场。按照Crouch等人提出的一种解析计算公式,并经Olson[14]改进后,其表达式为:

式中Cijns、Cijnn分别为平面应变弹性影响系数;Djs和Djn分别是各个微段上剪应力和正应力引起的不连续位移(即基于流固耦合计算而得到的裂缝宽度);Gij为Olson提出的三维修正系数,引入缝高和裂缝间距对附加应力场影响。
在数值计算中的每一时步都需计算该附加应力场,然后将其作用在地应力场上,用于进行延伸和起裂压力计算公式和迭代求解不同节点处的裂缝几何参数。
2 裂缝起裂与延伸判定准则

当压裂液进入天然缝,只要缝内压力大于裂缝面正应力及岩石抗张强度,将会开启天然缝并形成具有一定宽度的分支裂缝。根据裂缝面上正应力计算公式:式中T0为岩石抗张强度,MPa;σ为裂缝面正应力,MPa;σ2为垂向应力,MPa;σ1、σ3分别为水平应力,MPa;α、β、γ分别为裂缝面法线与主应力方向夹角。
可得到不同节点处的净压力为:

将不同节点处的净压力带入式(3)可得到裂缝起裂判定计算方程:

式中m为裂缝开启时对应的节点数,m≤n。
基于Erdogan提出的最大周向应力理论[15],可推导Ⅰ-Ⅱ复合型裂缝延伸角度方程:以及Ⅰ-Ⅱ复合型裂缝延伸判定计算方程:


3 复杂裂缝网络模型
模型假设条件:①天然裂缝都是垂直分布;②在无天然裂缝区域设定地层是均质、各向同性的连续线弹性体;③储层厚度较大,不发生穿层现象;④裂缝在垂直方向上的延伸速度小于在长度方向上的延伸速度。复杂裂缝网络模型包含以下控制方程。
1)起裂与延伸判定公式:见式(7)、(9)。
2)缝宽方程
假设产层足够厚,缝内净压pnet=pf(x,t)-σ′,σ′=σ+σin,得到裂缝横截面上任意z位置的缝宽方程为:

3)压降方程
根据Nolte平板间压降公式,并引入管道形状j(n)因子的方法,可得到缝内压降方程:

4)高度方程

5)连续性方程

模型初、边值条件与拟三维模型类似,但在裂缝相交后,交点处流量需重新平均分配。
式中xj为裂缝长度,m;wj(x,z,t)为缝宽,m;hj(x,t)为裂缝高度,m;pnet(x,t)为缝内压力,MPa;qj(x,t)为流量,m3/min;E 为杨氏模量,GPa;n为流态指数,无因次;K为稠度系数,Pa·sn;Ct为滤失系数,m·min-0.5;Aj为裂缝横切面积,m2;t为施工时间,min;τ(x)为t时刻液体到达缝内x处的时间,min;下标j代表缝网中某条分支缝。
改进的复杂裂缝模型求解方法如下所述。
1)先以二维PKN模型的缝长公式计算在不同时步下的初始裂缝长度:并根据井底或交点压力作为初始条件在缝长方向上以等压 降 值 划 分 计 算 节 点: (pnet+ Δp)(i)=,将得到的节点压力带入起裂判定方程计算实际能够开启的裂缝长度。
2)根据节点处的压力值,带入缝高方程求出不同节点处的缝高。
3)将得到的缝高和该节点处的压力带入缝宽方程可求解不同节点处的缝宽。
4)将前面求得的几何尺寸和初始流量分布带入压降方程,可得到节点处的新的压力值,此时需要对比前面等压降节点处的差值,并调整和拟合初始节点压力,使其满足|p′net(i)-pnet(i)|≤ε。
5)进一步将一维流动的连续性方程按照不同节点对应的参数值带入相应的缝宽、缝高值,以求出不同节点处的流量分布,将该流量值与初始假设的节点流量分布比较。若不一致,则改变初始流量分布关系式,重复第1步至第5步,最终实现流量拟合|q′(i)-q(i)|≤η。
6)在时步更新之前,需要考虑裂缝延伸判定条件,用该时刻的裂缝尖端方位、缝内压力值和附加应力场为已知条件判定裂缝是否会在下一个时刻继续扩展,并计算动态变化的延伸角。若满足条件则进入下一时步,重复步骤第1步至第6步,直至裂缝停止扩展。
针对页岩气压裂实际过程提出裂缝网络模拟程序流程如图2所示。

图2 复杂裂缝模拟流程图
4 模拟结果分析
4.1 裂缝延伸角度
根据延伸角计算公式,可分析水平地应力差、缝内净压和夹角对分支缝延伸轨迹的影响(图3)。
当水平应力差不变、缝内净压力的增大,延伸角度减小,分支缝延伸轨迹的曲率半径增大,不仅能有效扩大缝网宽度,也易于在空间上与其他缝相遇。而当净压力不变、水平应力差逐步增大时,延伸角变化越大,延伸轨迹的曲率半径减小,裂缝面在较小的范围内迅速垂直于最小主应力方向,使得缝内压力递减迅速,延伸或起裂难度加大。为提高压裂改造效果,应选取天然缝较为发育或者水平地应力差较小的适宜体积压裂的有利区块或层位,并通过优化施工参数和改进压裂材料,提高缝内净压力。
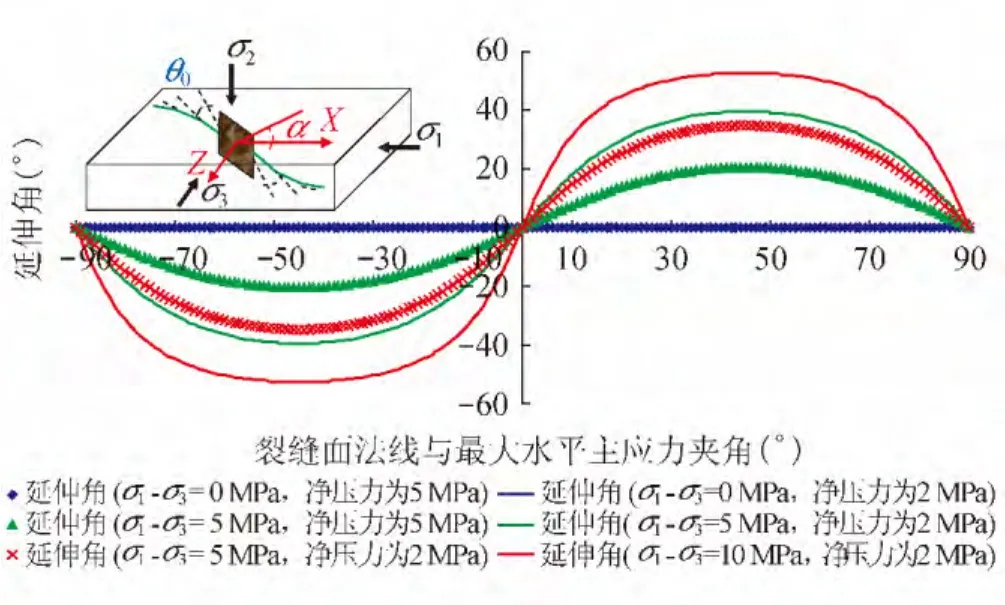
图3 裂缝延伸角变化关系图
4.2 裂缝延伸压力
根据裂缝延伸判断准则,定量分析水平应力差、裂缝半径、夹角、岩石断裂韧性对延伸所需压力的影响(图4)。
模拟结果表明:决定天然缝能否延伸的关键因素是自身长度和方位角,而岩石断裂韧性的变化对裂缝延伸压力的影响不明显。因此对于页岩气长水平井段压裂应选择天然缝发育程度较高,密度较大的区域射孔;在布井时不一定完全按照最小主应力方向,要充分考虑天然缝的走向对整个裂网形态影响。
4.3 复杂裂缝网络
根据页岩气压裂的“大液量、大排量、低黏度、低滤失”等特点,结合某海相页岩气井地质、施工参数,模拟了复杂裂缝网络形成过程和各分支裂缝几何尺寸,具体输入参数如下:水平最大主应力为37.5MPa,水平最小主应力为34.5MPa,杨氏模量为23.37GPa,泊松比为0.25,岩石抗张强度为3MPa,压裂液黏度为30mPa·s(施工/模拟可控关键变量),压裂液密度为1.02g/cm3,综合滤失系数为0.000 9m·min-0.5(施工/模拟可控关键变量),岩石断裂韧性为1.21MPa·m0.5,平均施工排量为8.5m3(施工/模拟可控关键变量),井底压力为55MPa(施工/模拟可控关键变量),计算时间步长为2min。天然缝参数位置随机分布,手动输入,与最小水平主应力方向夹角为±0°~40°,倾角为90°。
将整个缝网与微地震解释结果比较,几何尺寸能够实现与微震数据点分布范围的较好拟合,而且能够以裂缝复杂程度的差异形态解释数据点分布密度的变化(图5)。对比验证了模型计算结果,并能初步用于压裂设计优化。

图4 裂缝延伸压力变化关系图

图5 天然缝影响下裂缝延伸变化模拟图
5 结论
1)通过引入起裂与延伸判断准则、建立复杂裂缝网络模型、改进数值计算方法,实现了对含有大量天然缝的页岩气藏压裂裂缝网络的模拟研究,并结合微地震测试结果验证模型的准确性。
2)该模型实现了对页岩气体积压裂中非对称、不规则的复杂网络裂缝几何尺寸的计算,其成果可用于页岩气井压裂设计优化。
3)优选页岩气地质“甜点”应注重对天然裂缝长度、方位角、倾角、密度等物性参数的识别及描述,不仅是保证模拟结果可靠性的关键输入参量,而且是影响缝网几何尺寸及复杂性的物质基础。
4)对复杂裂缝网络模拟的最大难点就在于同时兼顾缝网复杂形态的分析和分支缝尺寸的计算,需要进一步在理论模型和数值解法上寻求新的突破。
[1] 王鸿勋,张士诚.水力压裂设计数值计算方法[M].北京:石油工业出版社,1998:178-186.Wang Hongxun,Zhang Shicheng.Numerical computation of hydraulic fracturing design[M].Beijing:Petroleum Industry Press,1998:178-186.
[2] WARPINSKI N R,TEUFEL L W.Influence of geologic discontinuities on hydraulic fracture propagation[J].Journal of Petroleum Technology,1987,39(2):209-220.
[3] FISHER M K,WRIGHT C A,DAVISON B M,et al.Integrating fracture mapping technologies to optimize stimulations in the Barnett Shale[C]∥paper 77441-MS presented at the SPE Annual Technical Conference and Exhibition,29 September -2October 2002,San Antonio,Texas,USA.New York:SPE,2002.
[4] BLANTON T L.An experimental study of interaction between hydraulically induced and pre-existing fractures[C]∥paper 10847-MS presented at the SPE Unconventional Gas Recovery Symposium,16-18May 1982,Pittsburgh,Pennsylvania,USA.New York:SPE,1982.
[5] 胡永全,贾锁刚,赵金洲,等.缝网压裂控制条件研究[J].西南石油大学学报:自然科学版,2013,35(4):126-132.HU Yongquan,JIA Suogang,ZHAO Jinzhou,et al.Study on controlling conditions in network hydraulic fracturing[J].Journal of Southwest Petroleum University:Science &Technology Edition,2013,35(4):126-132.
[6] WARPINSKI N R.Hydraulic fracturing in tight fissured media[J].Journal of Petroleum Technology,1991,43(2):146-152.
[7] BEUGELSDIJK L J,PATER D,SATO C J.Experimental hydraulic propagation in Multi-fractured Medium[C]∥paper 59419-MS presented at the SPE Asia Pacific Conference on Integrated Modelling for Asset Management,25-26A-pril 2000,Yokohama,Japan.New York:SPE,2000.
[8] 李勇明,彭瑀,王中泽.页岩气压裂增产机理与施工技术分析[J].西南石油大学学报:自然科学版,2013,35(2):91-96.LI Yongming,PENG Yu,WANG Zhongze.Analysis of shale gas fracture stimulation mechanism and operating techniques[J].Journal of Southwest Petroleum University:Science & Technology Edition,2013,35(2):91-96.
[9] 李进步,白建文,朱李安,等.苏里格气田致密砂岩气藏体积压裂技术与实践[J].天然气工业,2013,33(9):65-69.LI Jinbu,BAI Jianwen,ZHU Li′an,et al.Volume fracturing and its practices in Sulige tight sandstone gas reservoirs,Ordos Basin[J].Natural Gas Industry,2013,33(9):65-69.
[10] 程远方,李友志,时贤,等.页岩气体积压裂缝网模型分析及应用[J].天然气工业,2013,33(9):53-59.CHENG Yuanfang,LI Youzhi,SHI Xian,et al.Analysis and application of fracture network models of volume fracturing in shale gas reservoirs[J].Natural Gas Industry,2013,33(9):53-59.
[11] XU W,CALVEZ J L,THIERCELIN M.Characterization of hydraulically-induced fracture network using treatment and microseismic data in a tight-gas formation:A geomechanical approach[C]∥paper 125237-MS presented at the SPE Tight Gas Completions Conference,15-17June 2009,San Antonio,Texas,USA.New York:SPE,2009.
[12] WENG X,KRESSE O,COHEN C,et al.Modeling of hydraulic fracture network propagation in a naturally fractured formation[J].SPE Production & Operations,2001,26(4):368-380.
[13] WU X R,CARLSON A J.Weight functions and stress intensity factor solutions[M].Oxford:Pergamon Press,1991:78-82.
[14] OLSON J E,TALEGHANI A D.Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures[C]∥paper 119739-MS presented at the SPE Hydraulic Fracturing Technology Conference,19-21January 2009,the Woodlands,Texas,USA.New York:SPE 2009.
[15] 丁遂栋,孙利民.断裂力学[M].北京:机械工业出版社,1997.DING Suidong,SUN Limin.Fracture mechanics[M].Beijing:Engineering Industry Press,1997.

