高速铁路全并联AT牵引网短路故障情况下磁场环境特性分析
钱澄浩,何正友,高朝晖,王 斌
(西南交通大学 电气工程学院,四川 成都 610031)
0 引言
全并联自耦变压器(AT)供电系统是在原有复线AT牵引网的基础上将上行和下行线路在AT处通过横联线连接形成的。相比已有供电方式,全并联AT供电方式具有牵引网阻抗小、网损和电压降落低及抗干扰能力强等优点,有效改善了动车组的受电环境[1-2]。针对牵引供电系统供电功率大、供电区段长、可靠性高的需求,目前我国大多客运专线及城际铁路接触网均按全并联AT供电方式设计。但由于高速铁路牵引网露天架设,经受风雨冰霜、雷电及恶劣的环境污染,且无备用;同时,受电弓和接触网之间存在滑动接触,不断引起接触网的振动,引发接触网部件松动或断线脱落,常导致牵引网发生短路故障[3]。
国内外专家学者指出牵引网空间的磁场分布与牵引网线路中的电流分布密切相关,采集牵引网周围电磁场信息用于描述其运行状态是准确可靠的。目前针对牵引网电磁场分布的研究主要分为3个方向[4-7]:利用电磁工具测量出磁场分布;利用 Cason、有限元等理论进行电磁强度计算;建立模型进行电磁仿真分析。文献[8]针对意大利高速铁路低频电磁环境的特性,利用Maxwell 3D Ansoft软件对高速列车和牵引网进行二维、三维的磁场分布计算;文献[9]给出了详细的高速铁路动态电磁场分布公式,在Simulink中建立了完整的系统电磁仿真模型。但目前鲜有针对牵引网短路故障时空间磁场分布的研究。
全并联AT网具有半段效应,即在故障区段上、下行牵引网电流分布不对称,故障点短路电流是由相邻2个AT等比例提供。因此,发生短路的2条线路的电流大小和方向在故障点前后处会随着故障距离和过渡电阻的变化而变化。基于此,本文在仿真电流分布的基础上,研究了全并联AT牵引网发生不同类型短路时,故障点两侧的磁场环境变化,并分析了故障所在区段、过渡电阻、机车位置和运行工况对于故障后磁感应强度的影响。
1 基本磁场理论推导
1.1 测量单元位置的选取
根据某一实际全并联AT牵引网空间线路位置分布[10-11],建立全并联AT牵引网14导体模型,并假设坐标原点位于短路故障点所在切面,如图1所示。图中,各大写字母含义如下:T为接触线;R为钢轨;F为正馈线;PW为保护线;SW为承力索;GW为地线。
根据线路特点选取了磁场测量点的最佳放置位置P1和P2,由于z轴方向每隔一定距离放置1个测量单元,所以此处仅给出P1和P2的x轴、y轴最佳坐标为(-3.5,4.5)、(8.5,4.5)。选取 P1和 P2放置的原因为:与牵引网各导线的距离较为一致,不会因为靠近某一条线路而造成测量误差;在正常情形下,接触线和馈线中电流方向相反,产生的磁场相抵消,故障时有利于凸显特征;可忽略大地和综合地线回流对于测量的影响。
1.2 空间任意分布线路的磁场分析
牵引供电系统与电力系统类似,均通过多条平行导线的供电方式来传输电能。通过基本电磁学知识可知,无限长直导体在空间某处产生的磁感应强度和磁场强度大小与该点到导体之间的距离r成反比。由空间动态位的达朗贝尔方程和洛伦兹规范可知,一般变化电流分布 J(x′,t)所激发的矢势为:


图1 全并联AT牵引网14导体模型Fig.1 Model of all-parallel AT traction network with 14 conductors
其中,μ为相对磁导率;β为电流激励源角频率和磁场传输速度之比。
由式(1)可看出场点上的动态位和引起它的激励源δc存在时间上的差异,若激励源频率变化越快,则推迟势作用的效果越明显。考虑牵引网为工频交流供电,则空间中所产生的电磁波波长达到6000km,故在考察牵引网线路空间附近几十km范围内的磁场变化时都可看作是似稳场。所以通过测量牵引网空间磁场的有效值变化可以反映出牵引网线路中电流分布的变化。
然而牵引网线路在发生短路故障时,无限长直导线求解磁场的公式将不再适用,因此需对空间有限长直导线产生的磁场公式进行理论推导。为便于分析,考虑导线与直角坐标系中的z轴平行,如图2所示。

图2 有限长直导线三维磁场分析Fig.2 Three-dimensional magnetic field analysis for limited long straight wire
根据Bior-Savart定律可知,载流导体M1M2在场点产生的磁感应强度为:
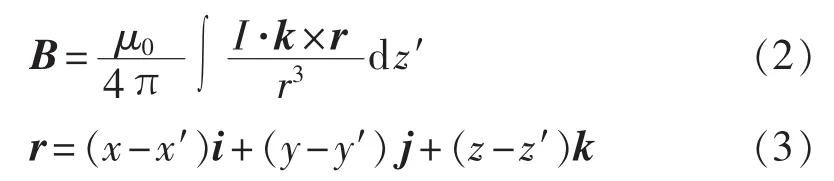
其中,μ0为真空磁导率常数;r为场点到源点的矢量;i、 j、k 分别为 x、y、z轴方向向量;电流 I如果沿着z轴正方向取正,沿着z轴负方向则取负。所以k×r可写为:

因此磁感应强度可写成分量表达式:


式(6)中Bz恒等于0,这与分析中假设导线与z轴平行有关,Bx、By分别为水平和垂直线圈测量到的磁感应强度的大小。若定义则的物理意义是场点处磁感应强度幅值的大小。磁感应强度B在Bx-By二维直角坐标系下不同象限时,θ的表达式为:

θ值描述了磁感应强度B的矢量相角。牵引网短路故障点两侧线路中,突变的电流大小和方向会导致牵引网空间磁场分布的变化,因线路空间分布位置不同,故不同短路故障类型在测量点处的磁感应强度亦会发生不同的变化。
2 全并联AT牵引网电流分布仿真
假设牵引网线路供电臂长45 km,每个AT段长15 km,即可把供电臂划分为3个AT区段,以某一实际线路的参数建立全并联AT网的仿真模型[12-14]。通过设置不同短路类型发生时的故障距离和过渡电阻可得到在不同情形下的电流分布图。例如,全并联AT上行牵引网在距离牵引变电所22.5 km处发生过渡电阻为5 Ω的T-R短路故障时,牵引网中的电流分布如图3所示,图中电流单位为A。

图3 电流分布Fig.3 Current distribution
由于全并联AT网具有上、下行完全对称的特点,所以图中非故障AT区段上、下行线路电流分布相同,而在故障AT区段上、下行牵引网线路中电流分布不同。这是因为当发生短路故障时,由于有过渡电阻的存在,短路点前后的电流方向不同。对于电压较高的导线,其电流流向为从线路两端流向故障点,而电压较低的导线电流流向为从故障点流向线路两端。
通过上述电流分布仿真的特征分析可知:当全并联AT网线路发生短路故障时,非故障AT区段上、下行线路同一距离处测量到的磁感应强度应大致相同;而在故障AT区段,由于上、下行牵引网中电流分布的大小不同,故导致同一距离处上、下行线路测量到的磁感应强度不同,且在短路故障点前后测量的磁感应强度会有明显不同。
3 磁场环境特性分析
为研究短路故障点两侧磁感应强度变化的特点,文中算例考虑了全并联AT牵引网发生不同类型短路故障时,故障区段、过渡电阻、故障距离以及机车运行位置和工况对于故障点两侧磁场环境所带来的影响。
3.1 故障AT区段对磁感应强度的影响
牵引网上存在电压波动,不同AT区段发生短路故障时,牵引网导线中电流分布不同,因此需要考虑短路故障点所在AT区段对于磁场环境的影响。当距离前一AT所5 km和9 km处发生过渡电阻5 Ω的牵引网T-F短路时,故障点两侧测量单元处的磁感应强度见表1。
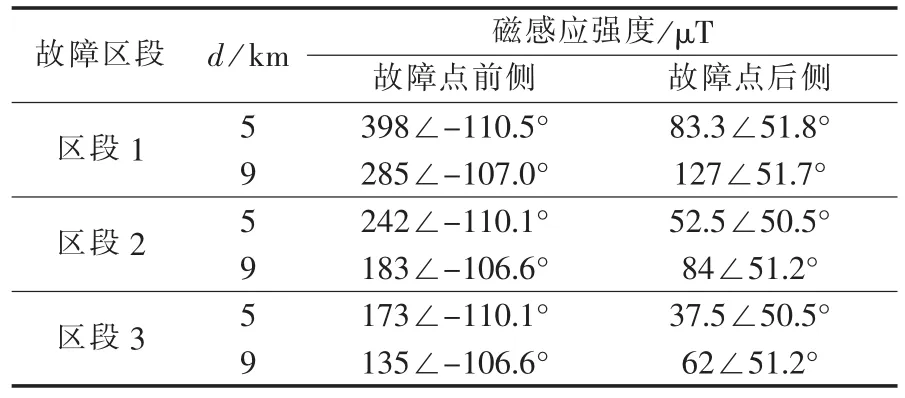
表1 故障区段对磁感应强度的影响Tab.1 Influence of faulty section on magnetic induction intensity
由表1可以看出,当故障点所在AT区段一定而与前一AT所的距离d不同时,故障点两侧测量点处的磁感应强度的幅值和相角都发生了较大的变化;但当短路故障与前一AT所的距离相同时,故障区段对于故障前后磁感应强度的幅值影响较大,而对相角的影响较小。通过对牵引网在不同位置处发生T-R、F-R短路故障的多组仿真结果表明,故障发生在不同AT区段对故障点两侧磁感应强度的相角影响不大。
3.2 过渡电阻和故障距离对磁感应强度的影响
短路故障发生时过渡电阻值和故障距离是随机变化的,因此有必要考察发生短路故障时,不同过渡电阻值和故障位置对于故障点两侧磁感应强度的影响。取短路故障均发生在AT区段2内,考察故障点距AT1所的距离在0~15 km范围内变化、过渡电阻在 0~50 Ω[15]范围内变化的情况下,故障点两侧磁场环境的变化,磁感应强度幅值和相角的仿真结果分别如图4、5所示。
由图4可看出:故障距离确定时,随着过渡电阻的不断增加,不同短路故障类型下测量到的磁感应强度的幅值都随之减小;当过渡电阻值确定时,随着短路故障点远离牵引变电所,在靠近牵引变电所侧,不同类型短路故障下测量到的磁场幅值均不断减小,而在远离牵引变电所侧,磁场幅值均不断增大。
从图5中可看出:当过渡电阻值确定时,不同类型短路故障下测量到的磁感应强度的相角随距离增加的变化不大。当过渡电阻变化时,不同类型短路故障下测量到的磁感应强度的相角在故障点两侧区别分明,并保持在一个互不重叠的范围内。

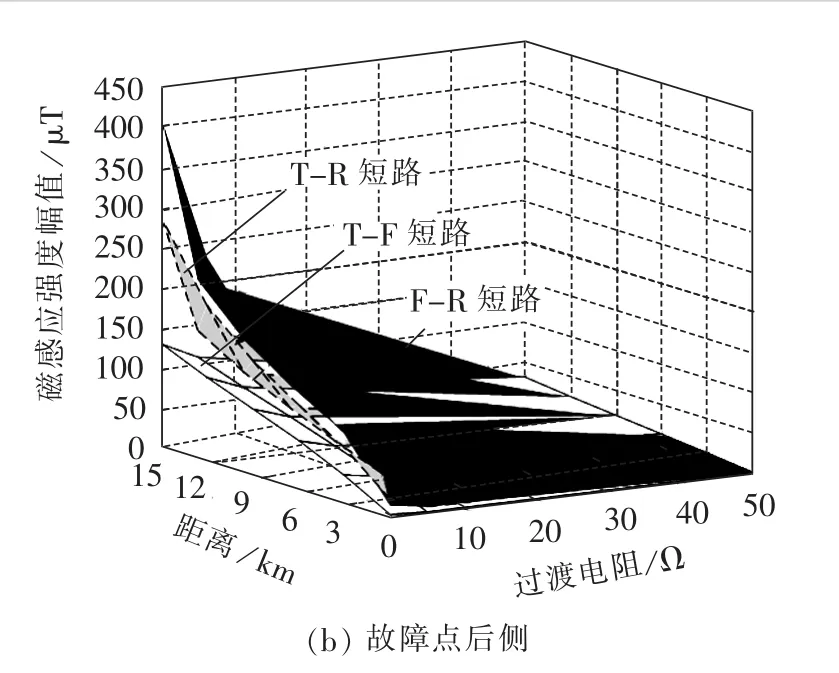
图4 过渡电阻和故障距离对磁感应强度的影响Fig.4 Influence of transition resistance and fault location on magnetic induction intensity

图5 过渡电阻和故障距离对磁感应相角的影响Fig.5 Influence of transition resistance and fault location on magnetic induction angle
3.3 机车对磁感应强度的影响
机车作为牵引供电系统的主要负载,具有瞬时移动和功率变化快的特点,所以在考察牵引网短路故障点两侧的磁场环境时,应计及机车运行位置和工况对测量单元量测结果所带来的影响[16]。
3.3.1 机车与故障点不在同一AT区段
假设牵引网在AT区段2的7.5 km处发生过渡电阻为5 Ω的T-F短路故障,考察机车分别行至AT区段1的9 km处(记为①)和AT区段3的6 km处(记为②)时,机车两侧和故障点两侧100 m处的磁感应强度大小。考虑高速动车组具有功率因数高的特点,可取 cos φ =0.96[17],并假设机车功率满负荷(10 MW)运行,计算可得机车阻抗为58+j17 Ω。磁场仿真结果如表2所示。

表2 机车与故障点不在同一AT段时的磁感应强度Tab.2 Magnetic induction intensity when train and fault point are in different AT sections
由表2可看出:当机车所在AT区段靠近牵引所时,机车两侧的磁感应强度未发生明显改变,这是因为机车等效阻抗一般大于过渡电阻;当机车所在AT区段远离牵引所时,虽然机车前后的电流变化引起了机车两侧磁场环境的变化,但因横联线的存在,机车所在AT段的电流相对较小,故机车两侧的磁场幅值变化较小。仿真结果显示,当机车与故障不在同一AT区段时,机车运行的位置对故障点两侧磁感应强度的幅值和相角影响都不大。
3.3.2 机车与故障点在同一AT区段
考虑机车与短路故障发生在同一AT区段内,假设牵引网在AT区段2的7.5 km处发生过渡电阻为5 Ω的T-F短路故障,考察机车分别行至AT区段2的4 km处(记为③)和10 km处(记为④)时,机车两侧和故障点两侧100 m处的磁感应强度大小。机车处于满负荷运行状态,磁场仿真结果如表3所示。

表3 机车与故障点在同一AT段时的磁感应强度Tab.3 Magnetic induction intensity when train and fault point are in same AT section
由表3可以看出,当机车运行在故障点所在AT区段内时,无论机车在故障点的前侧或后侧,机车两侧的磁感应强度的幅值和相角相差较小,但在故障点两侧的磁场环境却差别很大。通过比较可以看出,机车运行的位置对于故障点两侧的磁感应强度幅值影响很大,而对相角影响很小。
3.3.3 机车处于不同运行工况
高速动车组处于快速移动状态,在运行过程中可能会出现启动、加速、制动和惰行等不同的运行工况,因此需要考虑机车运行工况带来的影响。
假设牵引网在AT区段2的6 km处发生过渡电阻为5 Ω的T-F短路故障,牵引网电压取为25 kV;机车满负荷运行功率为10 MW,机车功率因数cosφ=0.96,运行在AT区段2的7.5 km处。通过计算可得出机车在满负荷、半负荷、空载3种运行状态下机车阻抗分别为 58+j17 Ω、115+j33 Ω、∞,故障点前后磁场相角结果如表4所示。

表4 机车不同运行工况时的磁感应强度Tab.4 Magnetic induction intensity for different operating conditions of train
由表4可知,机车处于这3种运行工况时,故障点两侧磁场环境的变化均不大,这是因为随着机车阻抗的增大,机车等效阻抗相比短路电阻也不断增大,机车运行工况对于牵引网短路故障点两侧磁场环境的影响会越小。
3.4 噪声对磁感应强度的影响
需要指出的是,上述仿真均建立在理想仿真信号的基础上,但牵引网空间磁场在不同环境背景下的变化十分复杂。表5给出了在不同噪声强度影响下短路故障点两侧的磁场环境[18],其中故障发生在AT区段2的7.5 km处,过渡电阻5 Ω。

表5 不同噪声强度下的磁感应强度Tab.5 Magnetic induction intensity for different noise intensities
由表5可知,在考虑噪声干扰的情况下,故障点两侧磁感应强度的幅值和相角均发生了较大的变化,当噪声强度增大到35 dB时,不同训练样本得到的结果均不相同,这说明强噪声条件下对于不同类型短路故障后的磁场环境具有较大的影响。
3.5 不同类型短路故障点两侧磁场分布统计
通过理论和仿真分析可知,当牵引网线路间发生短路故障时,在故障点两侧的磁感应强度的幅值变化明显,但统计发现无任何规律分布。磁感应强度的相角在故障点两侧象限偏转明显,经统计发现当外界噪声强度不大于45 dB时,故障点两侧相角分布基本符合以下规律。
a.故障点前侧磁感应强度的相角范围:T-R短路,-99°~-45°;T-F 短路,-116°~-100°;F-R 短路,-158°~-125°。
b.故障点后侧磁感应强度的相角范围:T-R短路,148°~162°;T-F 短路,38°~52°;F-R 短路,4°~13°。故障点两侧磁场测量相角分布如图6所示。

图6 故障点两侧磁场测量相角分布Fig.6 Measured magnetic induction angles at both sides of fault point
从图6中可以看出,在不同短路故障类型下,磁场相角分布不重叠,故障点两侧的磁场相角象限及范围均发生了大幅度偏转。
4 基于Ansoft Maxwell的仿真分析
实际牵引网专有导线具有非简谐横截面圆的特征,但上述理论分析中,对线路横截面利用等面元思想进行了简化处理[19]。因此有必要针对牵引网线路的专有截面进行仿真验证。
本文采用有限元分析软件Ansoft Maxwell 12进行仿真计算,建立了精确的导线仿真模型,其中考虑了牵引网专有导线(接触线、钢轨、馈线)的非简谐横截面的特征,根据实际情况设置了形状大小、材料属性、激励,在网格划分时考虑了导体的趋肤效应[20]。图7为当牵引网在AT区段2的3 km处发生过渡电阻为5 Ω的T-R短路故障时,在故障点前侧测量到的磁感应强度。

图7 牵引网空间磁场分布Fig.7 Spatial magnetic field distribution of traction system
由图7可以看出,测量点处的磁感应强度大小为204.22 μT,与本文中通过简化处理得到的该点磁感应强度理论结果(206 μT)误差为0.8%。仿真结果说明在考察牵引网专有线路空间磁场分布时,当场点距离导线足够远时,在测量精度范围内,用圆形截面的导线代替不考虑横截面形状的长直导线来计算磁感应强度的大小是合理的。
5 结论
本文在全并联AT牵引网电流分布仿真的基础上,通过选取特定位置的磁场测量点,仿真研究了牵引网发生短路故障后的磁场环境的变化,分析了不同环境特性对故障点两侧磁感应强度的影响。分析得出以下结论。
a.故障所在AT区段、过渡电阻值的大小、故障距离、机车所在位置和运行的工况对故障点两侧磁感应强度的幅值影响较大,而对相角的影响较小;外界环境噪声的强度对于磁场环境的影响较大。
b.当噪声信噪比大于45 dB时,不同类型短路故障发生后,在故障点两侧的磁感应强度的幅值变化无任何分布规律;但磁感应强度的相角在故障点两侧的象限及范围均发生了大幅度偏转,区分明显。
本文中分析的对象是较为理想情况下全并联AT牵引网线路电流仿真模型,模型中并没有计入承力索、保护线等线路的分流作用;本文没有考虑隧道壁内、分区所和AT所附近及多股道并联线路等复杂情况对牵引网空间磁场分布所带来的影响。本文仿真分析的结论可为通过测量磁场信息来实现牵引网故障类型的识别提供理论参考。

