基于小波去噪算法的主轴轴心轨迹提纯研究
籍永建,王红军,孟哲,柴富荣
(1.北京信息科技大学 现代测控技术教育部重点实验室,北京 100192)(2.北京信息科技大学 机电工程学院,北京 100192)
0 引言
一般情况下,把轴心相对于机座的运动轨迹称为轴心轨迹。轴心轨迹在与轴向垂直的平面内,能够反映转子在旋转过程中主轴上任一点在其旋转平面内相对于轴承座的运动轨迹,因此根据轴心轨迹的形状特征可以有效判断主轴系统的轴系故障[1]。然而由于在动态测量主轴轴心轨迹是以标准球或芯轴为测量目标,所以会将形状误差以及其它噪声信号叠加到轴心轨迹中。若想得到真实轴心轨迹就必须对采集信号进行去噪处理。
小波变换多分辨率的特点使其能够将原始信号从混有噪声的信号中提取出来。许多专家学者对小波理论进行了研究。D.L.Donoho在1995年提出阈值去噪方法去噪方法[2],L.K.Shark和C.Yu提出了最优模糊阈值消噪方法[3]。尽管国内外专家学者在小波阈值函数的改进方面做了大量研究,去的多种改进方法,但并不是所有的去噪方法都适用于主轴轴心轨迹信号的去噪。
1 阈值去噪方法
文献[4]详述了阈值去噪方法的原理等内容并提出一种软硬阈值折中方法。在小波阈值去噪方法中,其核心部分是小波系数的阈值处理或估计。由于不同的小波系数估计算法对应于不同的小波阈值去噪方法,所以产生了硬阈值方法和软阈值方法。
硬阈值函数表达式为如式(1)所示。

软阈值函数表达式如式(2)所示。
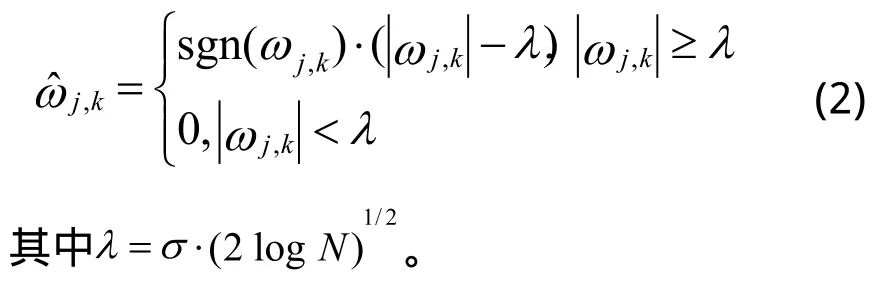
虽然软、硬阈值方法在实际中已经得到广泛应用,但是各有不足之处。硬阈值方法中j,k在λ与−λ处不连续;软阈值方法j,k整体连续性好,然而j,k与j,k之间存在恒定偏差,严重影响了信号重构的精度。
软硬阈值折中法如式(3)所示。

α为任意常数,10<α≤1,其取值由去噪效果决定。
西安电子科技大学张维强等[5]提出一种新的阈值函数用于去噪算法,并验证了此算法的有效性。
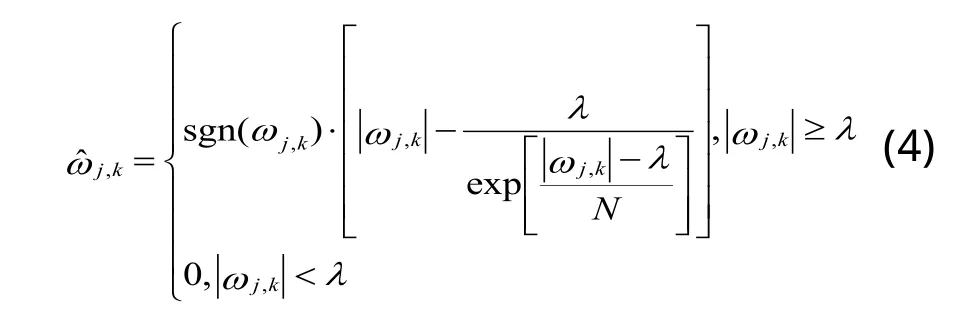
上式中,N为任意正整数。
刘恒冰等[6]构造的新阈值函数为:

2 实验对比分析
以上所提出的新阈值函数均由提出者进行了验证。但是三种改进阈值函数对于轴心轨迹的去噪效果需要试验验证。为了便于区分不同的方法,将式(3)对应的阈值函数方法称为方法一,式(4)对应的方法称为方法二,式(5)对应的方法称为方法三。利用采集的某数控机床回转误差数据进行验证。数据采集现场实验如图1所示。

图1 采集数据装置图
在进行对比分析时,选取的小波基函数为db6,分解层数为6。分别用上述三种方法对原始信号进行除噪处理,原始轴心轨迹图与三种不同方法去噪后生成的轴心轨迹图分别如图2、图3所示。

图2 原始轴心轨迹
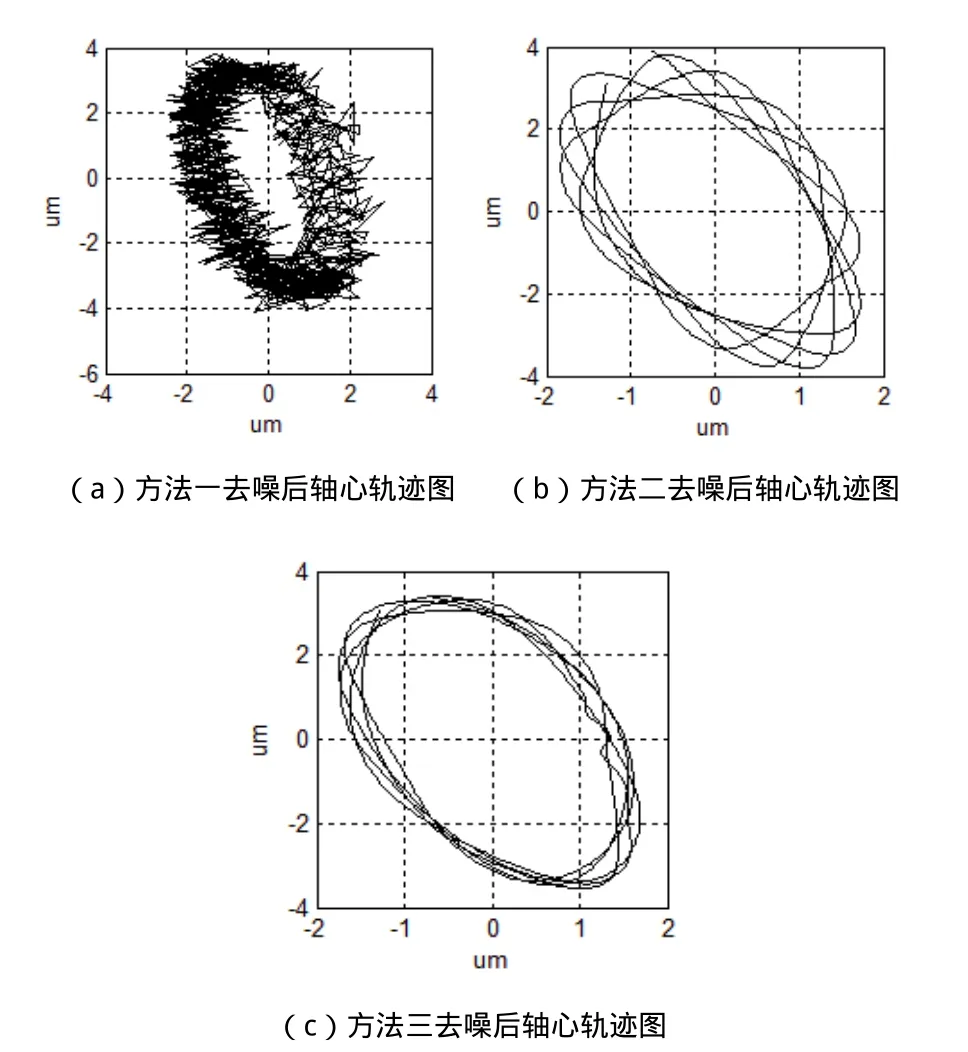
图3 去噪后轴心轨迹图
由图2可以看出,原始轴心轨迹中夹杂着大量的噪声信号,所以混杂难辨。若想得到纯净的轴心轨迹图必须进行降噪处理。图3中(a)、(b)、(c)图分别是利用方法一、方法二、方法三进行去噪后的轴心轨迹图。由图3可以看出,方法一的去噪效果最差。方法二、三的去噪效果差别不是特别明显,需要进一步评价。
3 去噪效果评价指标
常用的去噪效果评价指标有均方根误差(RMSE)[7]、信噪比(SNR)[8]、平滑度指标[9]。均方根误差指分解与重构信号与原始信号的均方根误差,其值越小表示去噪效果越好。计算式如式(7)所示。

信噪比指原始信号能量与噪声能量的比值,一般情况下,信噪比越高滤波效果越好。信噪比的定义式如式(8)所示。

powernoise=RMSE2,为噪声功率。
平滑度指标指去噪后信号的差分数的方差根与原始信号的差分数的方差根之比,一般情况下,去噪效果与平滑度指标数值成反比,即信号越光滑,平滑度指标的数值越小,去噪效果越好[10]。其计算方法如式(9)所示。


表1 三种方法对应的去噪效果评价指标
由表1可知,方法一的均方误差值最小,信噪比最大,但是平滑度远远高于其它两种方法,所以降噪效果不好。方法二、三的平滑度相同,但是,方法三的均方误差比方法二小,信噪比比方法二大,所以综合考虑以上因素,方法三的降噪效果最好。
4 结论
主轴的轴心轨迹中包含着大量的噪声信号,不同的去噪方法去噪效果也会不同。经过对比分析,可知方法三的降噪效果最好,在进行轴心轨迹分析时可利用方法三对采集的数据进行降噪处理,为进一步分析提供依据。但是去噪方法并不局限于论文中所提到的,随着相关理论的发展,各种降噪方法也在进一步完善。
[1]万鹏.基于流形学习的主轴系统故障诊断方法研究[D].北京信息科技大学.2012.
[2]Donoho David L.Denoising by soft-thresholding[J].IEEE Trans on Information Theory,1995,41(3):613-627.
[3]Shark L K and Yu C.Denoising Bu Optimal Fuzzy Thresholding in Wavelet Domain[J].IEEE Electronics letters,2000,36(6):581-582.
[4]朱艳芹,杨先麟.几种基于小波阈值去噪的改进方法[J].电子测试,2008(2):18-22.
[5]张维强,宋国乡.基于一种新的阈值函数的小波域信号去噪[J].西安电子科技大学学报,2004(02):296-299,303.
[6]刘恒冰,韩世勤,刘晶.基于新阈值函数及最优尺度的小波去噪研究[J].计算机工程与应用,2007,43(24):72-74,113.
[7]文鸿雁.基于小波理论的变形分析模型研究[D].武汉大学,2004.
[8]吴富梅,杨元喜.基于小波阈值消噪自适应滤波的GPS/INS 组合导航[J].测绘学报,2007,36(2):124-128.
[9]陶珂,朱建军.小波去噪质量评价方法的对比研究[J].大地测量与地球动力学,2012(02):128-133.
[10]陶珂,朱建军.多指标融合的小波去噪最佳分解尺度选择方法[J].测绘学报,2012,41(5):749-755.

