k-means融合FCM算法聚类研究
王 与,陈寿文
k-means融合FCM算法聚类研究
王 与,陈寿文
k-means融合FCM算法执行聚类过程,是在k-means算法完成聚类后,以其聚类结果作为FCM算法执行的初值,并通过FCM算法的执行完成。从结果分析可以看出,该算法聚类的效果比单纯使用FCM算法好,能够减少FCM算法循环体迭代运行次数并增强算法的鲁棒能力。
k-means算法; FCM算法; 混合均值算法
FCM 算法,也即模糊 C-均值聚类算法是由Dunn首先提出的,之后又被Bezdek加以推广[1]。因FCM算法运行机理简单,得到了广泛应用,然而通过具体分析其运行机理,发现该算法也存在如下局限性:①它没有考虑噪声指标的存在对数据分类的影响及样本特征指标间的相关性;②算法假定样本的各个特征指标对分类的贡献一致,无法刻画各个特征对分类的结果影响;③算法的性能依赖于初始聚类中心的选取,鲁棒性弱;④目标函数没有充分考虑到样本分布不均衡问题,且函数形式单一,仅采用了类内间距极小化的聚类准则,没有考虑类之间间距最大化以及各类之间的相互影响,使得算法易受噪声点的影响;⑤通常该算法只适用于数值型数据,不能直接运行于含有符号型属性的数据集上;⑥该算法具体模型中相应参数值的选取缺乏自适应性;⑦该算法在处理小量、低维的数据集是有效的,但其处理大量、高维的数据集耗时不能令人满意;⑧该算法是一种局部搜索优化算法,容易陷入局部收敛。
正是因为FCM算法存在上述的一些问题,这为其自身的进一步完善和发展创造了条件,许多学者针对不同的问题对其进行了改进。
如为了解决问题①和②,文献[2,3]提出了属性加权模糊聚类C-均值算法。FCM运行初始随机选用k个样本作为各个簇的中心,但存在初始点选取的不同造成聚类结果迥异的现象,文献[4]则采用了结合遗传算法优化初始中心点的做法对其进行改进,取得了很好的效果。针对问题④,文献[5,6]通过更改距离定义来改善样本不均衡问题。而对于问题⑤,文献[7]对 FCM 算法进行了适当处理后,提出了用于混合类型数据的聚类方法。就问题⑥而言,FCM算法模型中因其目标函数中引入了参数 m,就如何确定该参数的取值问题,文献[8,9]中对m的优选问题做了讨论,并指出选取的参考值为[1.5,2.5],通常选m=2。对问题⑦来说,FCM处理大量、高维数据集合时,文献[10]基于采样技术对FCM算法进行了改进,并结合遗传算法对聚类结果进行优化。对问题⑧来说,为了尽量克服FCM算法收敛于局部极小点,许多学者使用了具有全局搜索能力的智能算法对其进行改进,如文献[11]提出了一种基于改进遗传算法的模糊聚类方法,避免FCM算法容易陷入局部最优解的缺陷,文献[12]则提出了粒子群优化算法和FCM结合的聚类方法,同样获取全局最优聚类。
由于 FCM 算法对初始聚类中心比较敏感,本文将首先利用k-means聚类算法的运行结果来初始化FCM的聚类中心[13],并计算出FCM的初始隶属度矩阵,进而通过FCM算法的运行完成聚类任务,设计并实现一种k-means融合FCM的混合均值聚类算法。
1 预备知识
从隶属度的取值范围可以看出k-means算法为硬聚类算法,FCM算法为模糊聚类方法。为了便于对混合均值聚类算法进行描述,我们引入如下记号[14]。



2 混合均值聚类算法的数据流程图
本文对应的混合均值聚类算法实际为 FCM算法的改进,主要是利用 k-means算法的聚类结果信息来初始化FCM初始中心,通过增加FCM的预处理阶段,尽可能地克服因随机化处理致使聚类结果各异现象的产生。该算法的数据流图如图1所示。

图1 混合均值算法数据流图
2.1 混合均值聚类算法描述
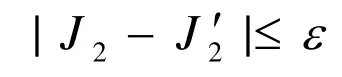

2.2 混合均值聚类算法实验及结果分析
本实验的运行环境为Matlab 7.0,实验中用到两个数据集:人工测试数据集(DS1)和UCI中的glass测试数据集。分别使用FCM算法和本文采取的混合均值聚类算法作用在这两个数据集上,并以聚类结果类内间距之和J为目标函数。
实验结果分析中,我们将结合两算法的收敛代数和样本错误划分率两个指标来比较各自聚类效果优劣性。测试数据集上运行聚类算法后,若各样本均能正确归类,则W=0,此时,通过比较收敛代数大小值便能区分各算法聚类优劣性;否则存在样本不能正确归类,则比较各算法循环体迭代次数相同时对应的错误划分率大小可判定聚类算法效果。若聚类结果相同,即:每次算法运行后第i个样本始终归属于某个类,此时,W为一常数值,通过比较收敛代数大小即可判定各算法聚类优劣性。
2.2.1 人工测试数据集聚类及其结果分析
本实验中DS1共有150个2维样本,分为3类,分别记为类A,类B和类C,各类均有50个样本。其中,类 A由 rand(50,2)产生,类 B由2+rand(50,2)产生,类C由4+rand(50,2)产生,该数据源以第1维为横坐标x,以第2维为纵坐标y,对应的散列图如图2所示。分别运行FCM算法和本文采取的混合均值聚类算法处理 DS1测试集,结果表明:二者均能实现各类样本正确归类。实验中,分别运行FCM算法和本文算法20次,目标函数收敛条件中设定 =0.001,二者对应的W=0,各算法收敛代数如图3所示。由图 3可知,FCM算法最小收敛代数为 3,而本文算法为 1;同时,本文算法收敛代数共有19次低于FCM算法,1次相等。另外,目标函数收敛时两算法各次运行总耗时如图4所示,由该图可知本文算法聚类耗时明显低于FCM算法。

图2 数据源DS1散列图

图3 目标函数收敛时两算法各自运行代数
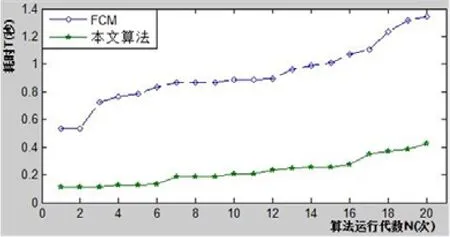
图4 目标函数收敛时两算法各次运行耗时

表1 glass原始数据的分类标准
2.2.2 Glass数据集聚类及其结果分析
Glass测试数据集包含214个9维样本,共分为6类(均用缩略词书写),各类中的数据个数如表1所示。定义向量=(x1,x2,x3,x4,x5,x6)代表聚类结果中属于第i类样本的数目,i∈{1,2,3,4,5,6},如:=(70,17,9,29,13,76)表示原始数据分类标准情形。目标函数收敛条件中设定 =0.001,分别运行两算法直至各自的聚类结果稳定,此时,6个类中各样本的分布向量=(60,27,7,36,18,66),对应W=39.3%,且各样本归类结果稳定(即第i个样本始终属于第j类),这增强了算法的鲁棒能力,也说明了FCM算法具有收敛性特点。两算法各自运行20次后,聚类结果均相同,对应各次算法收敛代数及两算法耗时如表2所示。由表2可知FCM算法最大收敛代数为 70,最小的为 28,本文算法最大收敛代数为19,最小的为 4。将两算法收敛代数绘制于同一坐标系,如图 5所示,由该图显见本文算法各次收敛代数均小于FCM算法,且二者平均收敛代数比值为0.2267:1。另外,两算法在目标函数收敛时各次运行总耗时如图6所示。由图6看来,本文算法运行耗时明显少于FCM算法,并且本文算法各次FCM阶段耗时均比FCM算法耗时少,对应耗时图如图7所示。

图6 FCM和文本算法总耗时
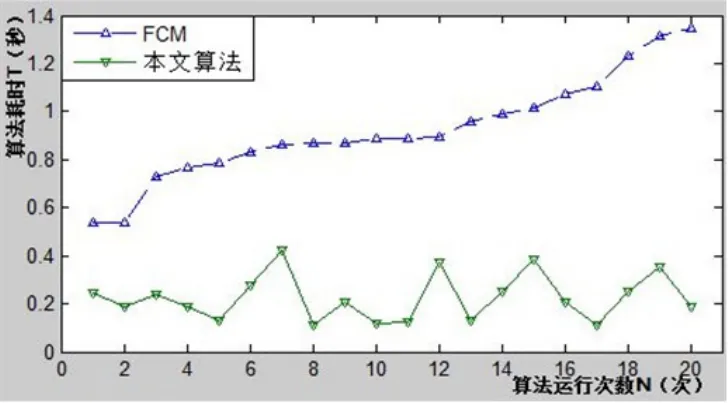
图7 FCM和文本算法FCM阶段耗时
3 结论
通过文中实验结果分析,该算法聚类的效果比单纯使用FCM算法好,能够减少FCM算法循环体迭代运行次数并增强算法的鲁棒能力。
[1] Bezdek J.C. Pattern recognition with fuzzy objective function algorithms[M]. New York: Plenum Press,1981:10-100.
[2] Wang, X. Z, Wang, Y. D, Wang, L. J. Improving fuzzy C-means clustering based on feature-weight learning[J].Pattern Recognition Letters,2004,25(10):1123-1132.
[3] 王丽娟,关守义,王晓龙等. 基于属性权重的 Fuzzy C Mean算法[J]. 计算机学报,2006,29(10):1797-1802.
[4] 董云影,张运杰,畅春玲. 改进的遗传模糊聚类算法[J].模糊系统与数学,2005,19(2):128-133.
[5] Wu,K. L, Yang, M. S. An alternative fuzzy c-means clustering algorithm[J].Pattern Recognition 2002,35(10):2267-2278.
[6] Zhang, D. Q, Chen, S. C. A comment on alternative C-means clustering algorithms[J]. Pattern Recognition,2004,37(2):173-174.
[7] Yang, M. S, Hwang, P. Y,Chen, D .H. Fuzzy clustering algorithms for mixed feature variables[J]. Fuzzy Sets and Systems, 2004,141(2):301-317.
[8] 高新波,裴继红,谢维信. 模糊c-均值聚类算法中加权指数m的研究[J]. 电子学报, 2000,28(4):80-83.
[9] 宫改云,高新波,伍忠东. FCM 聚类算法中模糊加权指数m的优选方法[J]. 模糊系统与数学, 2005,19(1):143-148.
[10] 陈松生,王蔚. 改进的快速模糊 C-均值聚类算法[J].计算机工程与应用,2007,43(10):167-169.
[11] 牛强,夏士雄,周勇,张磊. 改进的模糊 C-均值聚类方法[J]. 电子科技大学学报,2007,36(6):1257-1259.
[12] 唐贤伦,庄陵,李银国,曹长修. 基于粒子群优化和模糊c均值聚类的入侵检测[J]. 计算机工程,2008,34(4):13-15.
[13] 孙吉贵,刘杰,赵连宇. 聚类算法研究[J]. 软件学报,2008,19(1):48-61.
[14] 陈寿文,李明东.一种混合均值聚类算法的实现[J].计算机工程与应用,2010,46(18):132-13.
责任编辑:殷培峰
On the Hybrid Model Combined k-means with FCM for Clustering
Wang Yu, Chen Shouwen
Combiningk-means with FCM algorithm to execute clustering process refers to that we can take the results ofk-means clustering algorithm as a FCM initial value to complete clustering process. As can be seen from the results, the clustering effect is better than FCM. It must reduce the number of loop iterations and enhance the robustness of the algorithm.
K-means algorithm; FCM algorithm; Hybrid means algorithm
TP311
A
1673-1794(2014)05-0051-04
王 与,滁州学院数学与金融学院教师,硕士,研究方向:数据挖掘;陈寿文,滁州学院数学与金融学院(安徽 滁州 239000)。
滁州学院科研启动基金资助项目(2014qd011)
2014-03-03

