混合对数正态分布最大值的极限分布
黄建文, 罗远峰
(遵义师范学院数学与计算科学学院,贵州遵义563002)
1 预备知识
对于极值理论中指定分布的最大值分布的极限分布以及相应的赋范常数的研究是一个重点问题和难点问题.这一问题,有部分学者对此做了比较深入的研究和应用[1-8],对数正态分布的概率密度函数定义如下:对于x>0

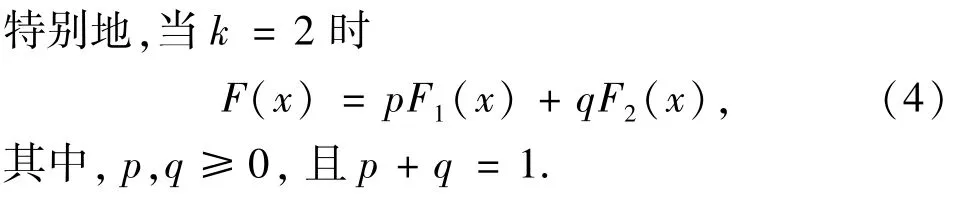
混合对数正态分布在现代统计的发展过程中作为一个模型得到广泛深入的研究和应用.关于混合对数正态分布的应用已有很多研究成果:M.Yang[10]对于模拟峰度和偏度研究标准的对数正态混合模型;H.Chrisfina等[11]考虑在一个保险政策中,假定索赔金额具有混合对数正态分布,研究得出给定参数值的中位数的分布服从对数正态分布;Y.Tian等[12]在均方损失函数下通过抽样算法研究对数正态分布混合模型的参数估计,而且通过一些模拟表明贝叶斯算法对他们的模型是有效的.S.Jamaludin等[13]引入几种类型的混合分布在描述和拟合马来西亚半岛每天降雨量的数据时,通过分析和检验,结果发现混合对数正态模型被认为是最佳的模型.L.Dietmar[14]构造出在Merton模型(Black-Scholes模型带跳)和随机波动模型中近似终端分布的混合对数正态分布,并将其应用于衍生品的定价和风险管理等方面.
本文主要研究同服从混合对数正态分布的独立随机变量、最大值的极限分布及其相应的规范化常数.主要结果给出了这一重要分布最大值的渐近形式.这2个命题的结论可以用于多元数据处理和参数估计中理论分析研究.
为了得到本文的主要结论,下面给出几个引理.这2个引理来自于参考文献[15].
2 辅助引理

3 主要结果


4 证明



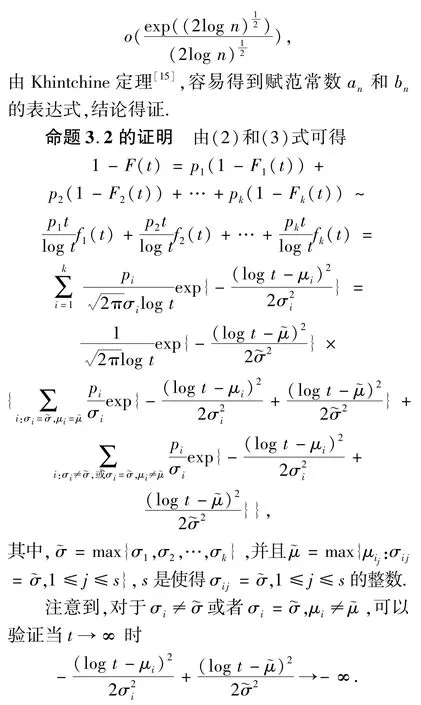

[1]熊芳,彭作祥.埃尔兰分布极值的收敛速度[J].西南大学学报:自然科学版,2011,33(3):5-8.
[2]帅玉亮,彭作祥.离散型随机变量幂赋范下最大值的极限分布[J].西南师范大学学报:自然科学版,2012,37(1):16-19.
[3]刘豹,彭作祥.有限混合短尾对称分布的极值分布[J].西南大学学报:自然科学版,2013,35(1):85-88.
[4]黄建文,陈守全,李文兴.广义logistic分布的收敛速度[J].四川大学学报:自然科学版,2014,51(1):47-52.
[5]杨红艳,彭作祥.有限混合偏正态极值的极限分布[J].西南大学学报:自然科学版,2014,36(3):59-62.
[6]徐明媛.常见概率分布相互关系及极限定理[J].四川师范大学学报:自然科学版,1987,9(3):28-34.
[7]Chen S,Huang J.Rates of convergence of extreme for asymmetric normal distribution[J].Stati Prob Lett,2014,84:158-168.
[8]Liao X,Peng Z,Nadarajah S,et al.Rates of convergence of extremes from skew-normal samples[J].Stat Prob Lett,2014,84:40-17.
[9]Liao X,Peng Z.Convergence rates of limit distribution of maxima of lognormal samples[J].J Math Anal Appl,2012,395(2):643-653.
[10]Yang M.Normal log-normal mixture,leptokurtosis and skewness[J].Appl Econ Lett,2008,15(9):737-742.
[11]Chrisfina H,Jacques C.Mixed lognormal distributions[J].Actuarial Research Clearing House,1994,2:215-220.
[12]Tian Y,Liu Y,Chen P.Bayesian analysis for a mixture of log-normal distributions[J].Sci Magna,2010,6(1):65-71.
[13]Jamaludin S,Kong C,Yusof F,et al.Introducing the mixed distribution in fitting rainfall data[J].Open J Modern Hydrology,2011,1(2):11-22.
[14]Dietmar L.Mixed lognormal distributions for derivatives pricing and risk-management[J].Society for Computational Economics:Computing in Economics and Finance,2004,48:1-30.
[15]Leadbetter M R,Lindgren G,Rootzen H.Extremes and Related Properties of Random Sequences and Processes[M].New York:Springer-Verlag,1983:5-27.
[16]Peng Z,Weng Z,Nadarajah S.Rates of convergence of extremes for mixed exponential distributions[J].Math Comput Simulation,2010(1),81:92-99.
[17]Peng Z,Tong B,Nadarajah S.Tail behavior of the general error distribution[J].Communications in Statistics:Theory and Methods,2009,38(11):1884-1892.
[18]刘豹,付颖.麦克斯韦分布的逐点收敛速度[J].西南大学学报:自然科学版,2013,35(5):80-83.
[19]Lin F,Peng Z.Tail behavior and extremes of short-tailed symmetric distribution[J].Communications in Statistics:Theory and Methods,2010,39(15):2811-2817.
[20]Lin F,Jiang Y.A General version of the short-tailed symmetric distribution[J].Communications in Statistics:Theory and Methods,2012,41(12):2088-2095.
[21]Liao X,Peng Z,Nadarajah S.Tail properties and asymptotic expansions for the maximum of the logarithmic skew-normal distribution[J].J Appl Probability,2013,50(3):900-907.
[22]Liao X,Peng Z,Nadarajah S.Tail Behavior and Limit Distribution of Maximum of Logarithmic General Error Distribution[R].Manchester:Manchester University,2012.
[23]刘姣姣,陈守全.广义指数分布随机变量序列最大值的收敛速度[J].西南大学学报:自然科学版,2013,35(5):89-92.
[24]Mladenovic P.Extreme values of the sequences of independent random variables with mixed distributions[J].Matematicki Vesnik,1999,51(1/2):29-37.
[25]Figueiredo A T,Jain A K.Unsupervised learning of finite mixtures models[J].IEEE Transportations on Pattern Analysis and Machine Intelligence,2002,24(3):381-396.

