一种靶场电磁环境复杂度评估方法＊

彭 武，何怡刚，2，方葛丰，樊晓腾

（1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.合肥工业大学电气与自动化工程学院，安徽 合肥 230009；3.电子测试技术国防科技重点实验室，山东 青岛 266555）

1 引言

电磁环境的定性和定量分级，是在电磁环境日益复杂的情况下，有效应对电磁环境问题所提出的必然要求，是控制电磁环境、实现区域频谱管理智能化的基础。20世纪60年代初，脉冲雷达和高灵敏度接收机的出现导致高脉冲密度的战场电磁环境和电磁信号堵塞，为了预测未来电磁环境的状态，Tetley［1］提出了基于计算机模拟的数学模型解析预测电磁环境的方法。近年来，国内已有不少学者对电磁信号环境复杂度评估进行了初步研究。如采用空域特征、时域特征、频域特征和功率域特征的“四域法”进行定性描述和定量分析［2］，提出了层次分析法AHP（Analytic Hierarchy Process）［3］、D－S证据理论［4］、多元联系数法［5］等。

传统方法主要依赖于人的经验，权值的设定具有主观性，一旦需要对权值进行修改，过程变得非常复杂。战场电磁环境复杂多变，不同的作场区域考虑的因素不同，因此需要经常对权值进行修改，所以传统方法的应用有一定的局限性。前馈BP（Back Propagation）神经网络（又称误差反向传播网络）具有联想与记忆能力，权值通过学习与训练得到，具有自适应特性，且权值反映了多因素之间高度非线性的复杂关系，可以有效地建立高精度模型并进行模式识别。为此，本文提出基于BP神经网络的电磁环境复杂度评估方法。

2 靶场电磁环境模型

根据靶场电磁信号的特点［6］，一般可以采用如下各个参数对其复杂度进行从时域到频域方面的分析。

2.1 频谱占用度

频谱占用度是指在电磁信号环境中，电磁信号合成强度与背景电磁噪声强度之和超过指定环境电平门限S0时，所占的频段宽度与己方作战可用频率资源的比值，它反映的是在指定电磁环境电平门限的情况下，可供电子设备使用的备用频率资源的多少。

令St为背景信号在时域内的能量平均值，计算公式为：

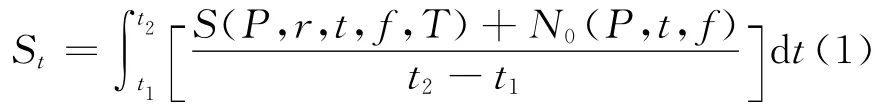
其中，t1、t2为作战起止时间，S（P，r，t，f，T）为电磁信号合成时变功率谱密度，N0（P，t，f）为电磁背景噪声强度的统计值。

则频谱占用度为：

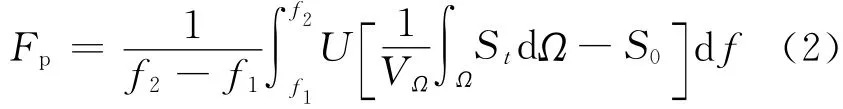
其中，下标p为占用度说明性字母，f1、f2为可用频率资源上下限，Ω为作战空域，VΩ为作战空域体积，U（x）为单位阶跃函数：

2.2 时间占用度

时间占用度是指在战场电磁信号环境中，战场电磁信号合成强度与战场背景电磁噪声强度之和超过指定环境电磁门限S0所占用的时间长度与整个作战时间的比值，时间占有度大，表明电子设备可正常工作的时间就少。

令Sf为背景信号在频域内的能量平均值，计算公式为：

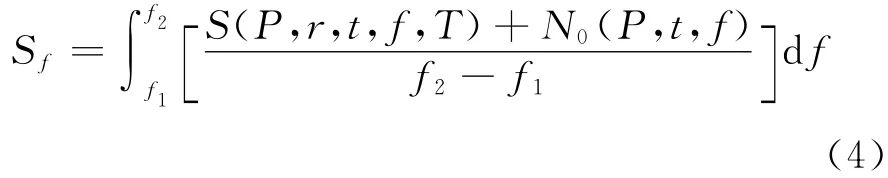
则时间占用度为：

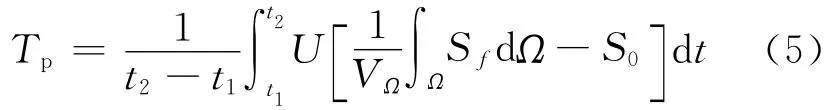
公式（4）和公式（5）中的变量含义与公式（1）和公式（2）中的变量含义相同。

2.3 空域覆盖率

空域覆盖率表示战场上各种信号叠加后的战场电磁信号合成强度与战场背景电磁噪声强度之和超过指定环境电平门限S0所占用的空间范围与整个作战空间范围的比值，它反映的是战场电磁信号环境与电子设备在空域上的冲突。

令Sa为背景信号在空域内的能量平均值，计算公式为：

则空域占用度为：

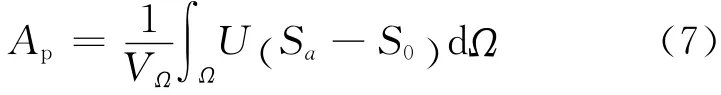
公式（6）和公式（7）中的变量含义与公式（1）和公式（2）中的变量含义相同。

2.4 靶场电磁背景平均功率谱密度

电磁背景平均功率谱密度是指在一定作战空间、作战时间段和作战用频范围内，各种信号叠加后的战场电磁背景环境的平均功率谱密度，它反映的是战场电磁背景环境在能量角度的强弱程度。平均功率谱密度Saver的表达式为：

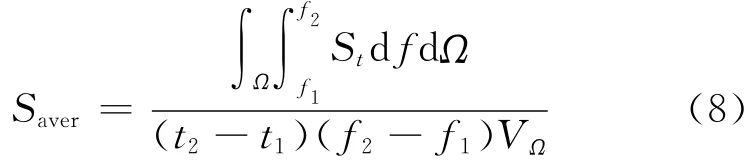
式（8）中的变量含义与式（1）和式（2）中的变量含义相同。

2.5 靶场电磁环境客观复杂性的定级标准

根据靶场电磁环境客观复杂性评估指标值与靶场电子设备的作战使用及其抗干扰电平门限之间的冲突程度，来确定靶场电磁环境的复杂程度，具体的评价标准可参照表1。

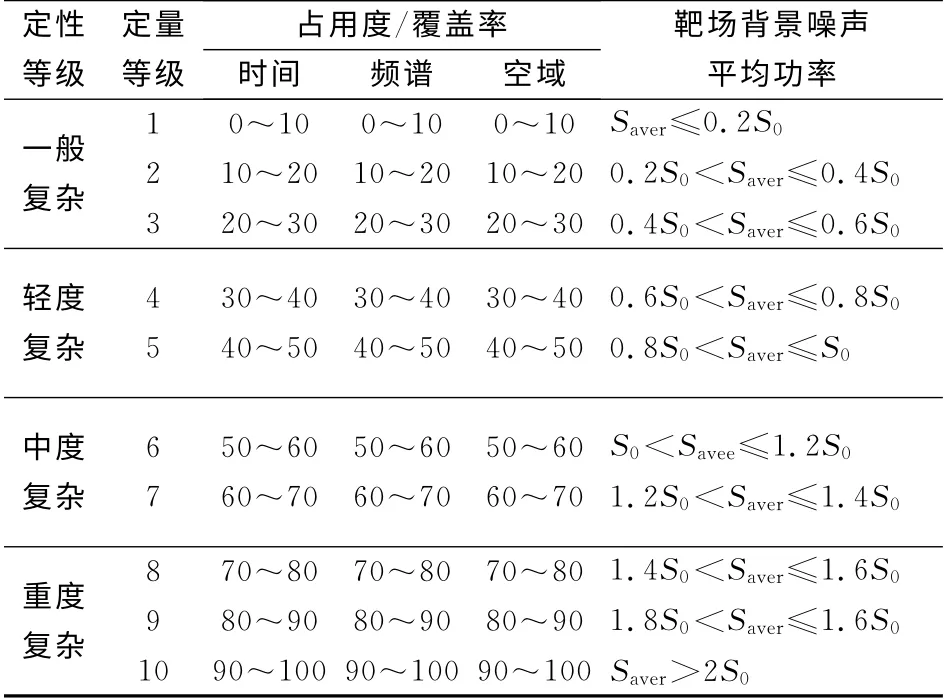
Table 1 Grading standard of range electromagnetic environment表1 靶场电磁环境复杂度的定级标准 %

3 评估方法对比分析

3.1 传统方法的优缺点

四域法从定性的方面出发，描述了电磁环境复杂度评估的四个具体指标及其计算方法，给出了电磁环境客观复杂性的定性标准。该标准利用4个评估指标和10个复杂等级将电磁环境划分为104类，具有重要的参考价值。不足的是，由于在评估指标中没有引入权值，方法只能对10类电磁环境进行定性分类，使得该方法的应用受到限制。

层次分析法（AHP）建立了评估人为电磁环境的递阶层次结构，细化了评估指标。但是，AHP标度准则是通过咨询专家意见建立的，因此受人为因素影响较大，不利于算法的稳定实现。

D－S证据理论采用模糊数学方法对电磁环境进行了新的复杂等级划分，弥补了专家打分法的不足，提供了一种电磁环境复杂度评估新途径。但是，模糊算法有自身的缺点：首先，模糊控制规则是根据专家的经验设定的，很难避免带有一定的主观性；其次，控制规则一旦制定就不能根据外界条件的变化进行调整，自适应性能差。

多元联系数法与AHP法类似，需要人为设定权值因子。例如，文献［5］中选择五元联系数，权值因子为（－1，－0.5，0，0.5，1），这些权值因子由专家设定，但是不同的专家之间难以形成统一，因此不具有普遍特性。

3.2 BP神经网络方法的优势

与传统方法相比，BP神经网络方法用于靶场电磁环境复杂度评估有以下优点：

（1）权值自适应。权值是评估指标到复杂度定量结果之间的桥梁，是衡量评估指标重要程度的关键所在，同时也确保了神经网络良好的逼近能力。BP神经网络经学习与训练后可得到一组权值矩阵和阈值矩阵，矩阵的大小随电磁环境模型要求的精度不同而改变，具有自适应特性。

（2）抗干扰和稳定性。与AHP法不同，BP方法不需要专家根据经验设定权值的大小。网络中的权值是通过神经网络训练获得的，不受人为因素的干扰；其次，训练得到的权值、阈值可以进行保存，不仅便于硬件实现，而且避免了网络重复训练，可以起到稳定发挥BP神经网络的评估作用。

（3）模式识别能力。BP神经网络实现了一个从输入到输出的映射功能，只需要很少的样本，就可以通过训练建立一个非线性网络，在保证训练样本分类正确的情况下，还能对未见过的模式或有噪声污染的模式进行正确分类，具有泛化能力与容错能力。

4 BP神经网络的结构

4.1 实验参数的确定

基于BP算法的多层前馈型网络［7］，以表1中所示的时间占用度、频谱占用度、空域覆盖率、靶场背景噪声平均功率等四个指标为输入变量，以电磁环境复杂度为输出变量，采用21个训练样本，每个样本有4个分量，最终确定输入矩阵P以及目标矩阵T为：

为加快BP神经网络训练速度，将靶场背景噪声平均功率进行预处理，令背景噪声平均功率比Sp为：

其中，Sp的下标p为占用度说明性字母，Sp的变化范围为［0，100］，与其它三个评估指标变化范围相同，有利于数据的归一化处理，可以提高神经网络的训练速度。

4.2 隐层结构的确定

BP网络隐层神经元的多少和BP网络逼近能力之间有很大相关性，不同隐层单元数与网络达到收敛所需步数的关系如图1所示。

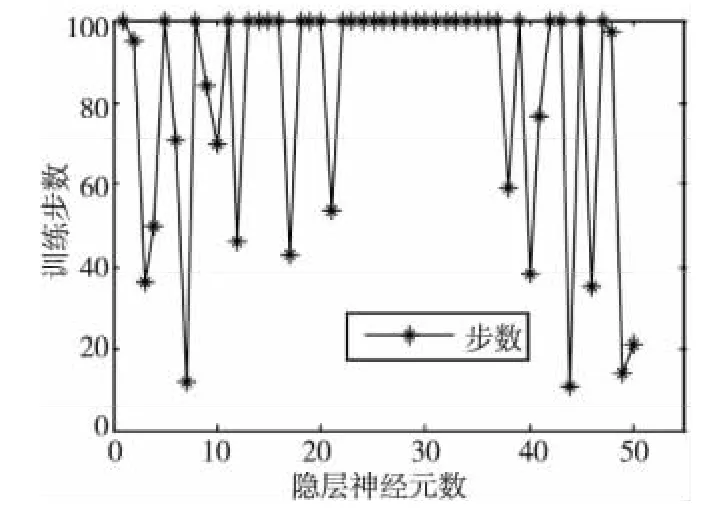
Figure 1 Relationship between the number of neurous in hidden layer and training steps图1 隐层神经元个数与训练步数的关系

从图1中可以看出，隐层神经元个数较少时，达到所需精度的训练步数多，且出现震荡。随着神经元个数的增加，网络收敛性能得到了改善，但是神经元个数过多时，容易引起过拟合，收敛速度又变慢。

如何确定隐层层数的问题，已有不少学者对此作了研究。一般地，在选择隐层神经元数时有三个经验公式：，其中，k为样本数，ni为隐单元数，n为输入单元数。如果i＞n1，则

（3）n1＝log2n，其中，n为输入单元数。

但是，这几个公式有一定的局限性，这样计算得到的隐层神经元数目容易导致学习时间过长、误差大、容错性能差等后果［8，9］。

Table 2 Selection process of cross validation method表2 交叉证实法选择过程

本文采用交叉证实法（Corss Validation）［10］来选择隐层单元数，它通过比较不同隐层单元数的神经网络多次训练结果的证实误差算术平均值的大小来确定隐层的优劣，该方法选择的隐层可以使BP神经网络较好地拟合训练集的数据。计算公式为：

其中，M为样本子集数，MPSEm为抽出子集的证实误差。本实验中有21个训练样本，每个样本有4个分量，不妨令子集数为4，此外，选取证实误差的标准差σMPSE一起作为衡量指标。公式（10）所示交叉证实法选择过程如表2所示。

通过比较和分析，最终确定选择10个隐层单元，得到的BP网络结构如图2所示。其中，IW表示隐层神经元的权值，b表示隐层神经元的阈值。

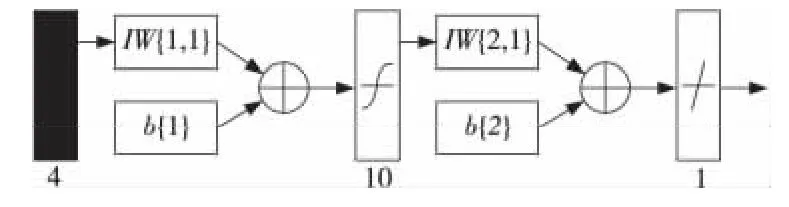
Figure 2 Structure of neural in adaptive layer method图2 自适应隐层法得到的神经网络结构

4.3 训练函数的选择

采用不同的训练函数对网络的性能有很大的影响，比如收敛速度等［11］。表3给出了不同训练方法收敛速度对比（对应的网络结构为单隐层，传递函数第一层为tansig，第二层为purelin），在综合分析了多种训练过程后，认为采用LM（Levenberg－Marquardt，在Matlab中为trainlm函数）算法收敛速度最快，在13步时误差仅为6.101 2e－6（均方误差曲线如图3所示）。

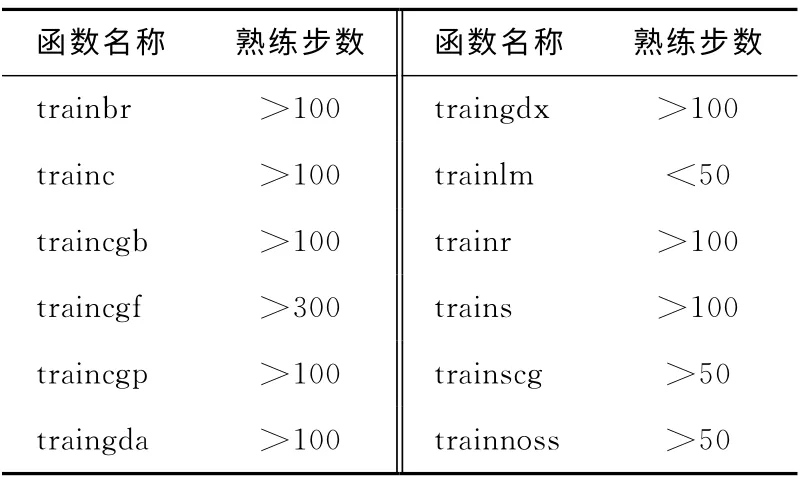
Table 3 Convergence speed comparison in different training ways表3 不同训练方法收敛速度对比

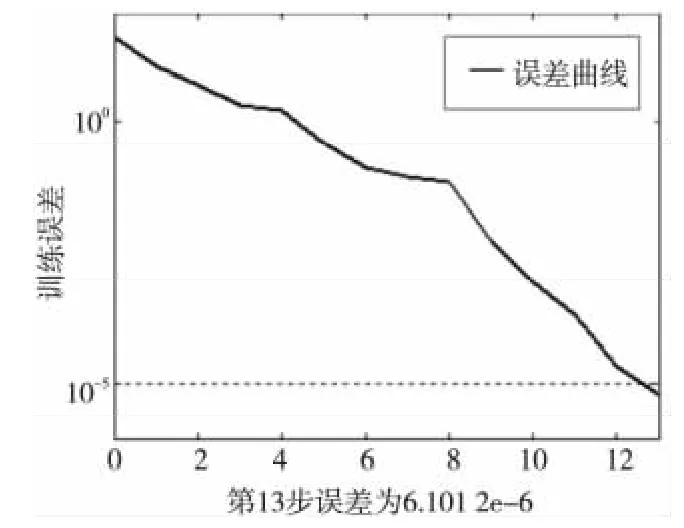
Figure 3 Mean square error curve using LM training algorithm图3 采用LM训练算法的均方误差曲线

5 实验结果与分析

运用Matlab神经网络工具箱，根据输入输出向量创建BP神经网络，按照所要求的精度进行训练，从而得到了输入层、隐层、输出层的权值与阈值。因为这些权阈保存了网络的非线性映射关系，所以训练后将这些权值用矩阵形式进行保存，从而避免神经网络的反复训练，节省训练时间（复杂度评估流程图如图4所示）。

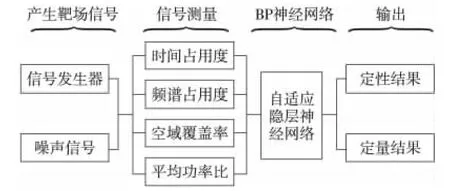
Figure 4 Complexity evaluation flow图4 复杂度评估流程图

针对几种不同的复杂度评估方法在不同电磁环境下进行了测试，得到了靶场电磁环境的定性与定量结果，测试结果如表4所示。

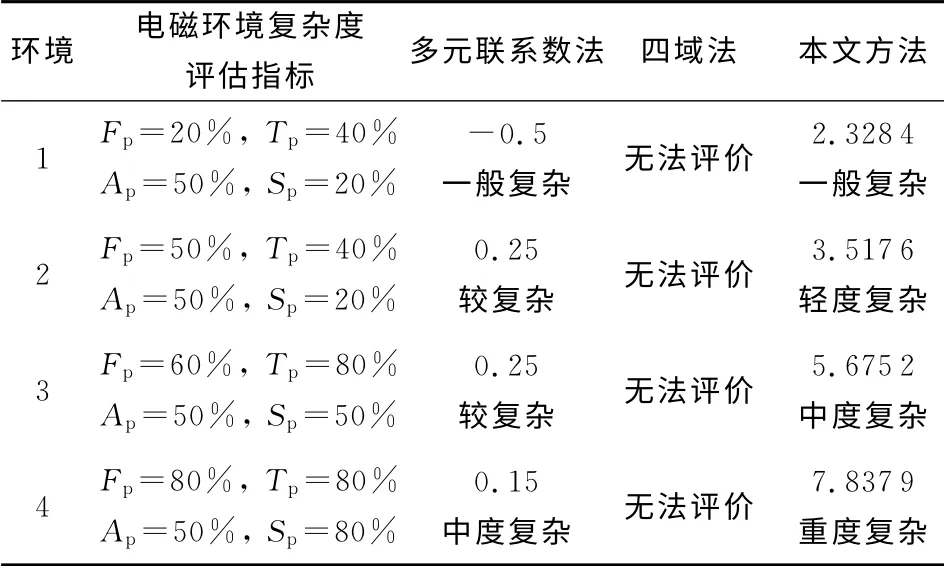
Table 4 Complexity evalution results in different range electromagnetic environment with different methods表4 不同方法在不同靶场电磁环境中复杂度的评估结果

由表4可以得知，当Fp＝20%，Tp＝40%，Ap＝50%，Sp＝20%时，这类模式空域覆盖率较大，不在表1所表示规则内，因此“四域法”不能对其进行评估；从第4种环境中可以看出，多元联系数法（四个权值分别为1、0.5、－0.5和－1）虽然可以进行复杂度评估，但是得出的结论却不合理，因为四个评估指标都达到50%以上，且其中时间占用度、频谱占用度、背景噪声平均功率比三个指标都已经达到80%，中度复杂的评估结果显然不够，应该采用本文方法的评估结果（重度复杂）较好。

综上可知，BP神经网络方法不仅可以进行各种电磁环境下的复杂度评估，而且评估结果更合理，且算法稳定可靠，明显优于传统方法。

6 结束语

本文提出了基于BP神经网络的靶场电磁环境的复杂度评估新方法，克服了传统方法受人为经验因素影响的不足。对复杂度评估指标进行了预处理，简化了映射规则，提高了训练速度，改善了BP神经网络的收敛性能。实验表明，BP神经网络方法能够对传统电磁环境复杂度定级标准中没有覆盖的规则进行识别，实现了电磁环境的定性和定量分级。今后的研究将进一步探讨神经网络算法的数值优化以及与模糊算法、遗传算法相结合的应用。

［1］ Tetley W H.Analytical prediction of electromagnetic environments［J］.IRE Transactions on Communications Systems，1961，9（2）：175－185.

［2］ Wang Zhi－gang，Wang Fang，Zhao Zhi－qiang.Analysis and evaluation for external complexity of battlefield electromagnetic environment［J］.Modern Defence Technology，2010，38（3）：19－24.（in Chinese）

［3］ Dong Zhi－yong，Li Qiang.Complexity evaluation of artificial electromagnetism environment based on AHP［J］.Command Control and Simulation，2008，30（5）：106－110.（in Chinese）

［4］ Dai He－peng，Su Dong－lin.Study of the complexity evaluation on electromagnetism environment［J］.Journal of Microwaves，2009，25（3）：25－27.（in Chinese）

［5］ Wang Zhi－gang，He Jun.Complexity evaluation method of battlefield electromagnetic environment based on multivariate connection number model［J］.Electronic Information Warfare Technology，2008，23（2）：50－53.（in Chinese）

［6］ Liu Pei－guo.The basement of electromagnetic environment［M］.Xi’an：Xi’an Electronic and Science University Press，2010.（in Chinese）

［7］ Song Yi－bin，Wang Pei－jin.An improved BP algorithm for FNN and its application［J］.Computer Engineering，2003，29（14）：109－111.（in Chinese）

［8］ Xu Li－ping，Jiang Hong，Zhang Yan－hua.Modified model selection in neural networks［J］.Computer Engineering，2001，27（2）：72－73.（in Chinese）

［9］ Li Wen－sheng，Xie Mei，Deng Chun－jian，et al.Dynamic gesture learning and recognition based on the Hermite neural network［J］.Computer Engineering ＆Science，2012，34（2）：116－122.（in Chinese）

［10］ Xu Li－ping，Zhang Yan－hua.Another criterion to judge performance of neural networks［J］.Journal of Shanghai Jiaotong University，2002，36（7）：980－983.（in Chinese）

［11］ Xiao Hong，Cao Mao－jun，Li Pan－chi，et al.Process neural network training based on piecewise linear interpolation［J］.Computer Engineering，2011，37（20）：211－215.（in Chinese）

附中文参考文献：

［2］ 王志刚，王芳，赵志强.战场电磁环境客观复杂性分析与评估［J］.现代防御技术，2010，38（3）：19－24.

［3］ 董志勇，栗强.基于层次分析法的人为电磁环境复杂程度评估［J］.指挥控制与仿真，2008，30（5）：106－110.

［4］ 代合鹏，苏东林.电磁环境复杂度定量分析方法研究［J］.微波学报，2009，25（3）：25－27.

［5］ 王志刚，何俊.战场电磁环境复杂性定量评估方法研究［J］.电子信息对抗技术，2008，23（2）：50－53.

［6］ 刘培国.电磁环境基础［M］.西安：西安电子科技大学出版社，2010.

［7］ 宋宜斌，王培进.多层前馈神经网络改进算法及其应用［J］.计算机工程，2003，29（14）：109－111.

［8］ 徐力平，江红，张炎华.改进的选择神经网络结构的方法［J］.计算机工程，2001，27（2）：72－73.

［9］ 李文生，解梅，邓春健，等.基于Hermite神经网络的动态手势学习和识别［J］.计算机工程与科学，2012，34（2）：116－122.

［10］ 徐力平，张炎华.评价神经网络拟合精度的另一个指标［J］.上海交通大学学报，2002，36（7）：980－983.

［11］ 肖红，曹茂俊，李盼池，等.基于分段线性插值的过程神经网络训练［J］.计算机工程，2011，37（20）：211－215.