非线性优化PID控制在桥式起重机防摆中的应用*
刘辉 黄国健 勉智
(广州特种机电设备检测研究院)
0 引言
桥式起重机是现代生产中一种重要的搬运机械设备,在各个生产领域都有广泛的应用。然而桥式起重机在作业过程中,由于小车的加速度和负载的提升动作以及风、摩擦引起的扰动等,产生负载摆动,从而在整个系统水平方向上形成周期性的动力学激励,严重影响工作效率,并增加起重装卸作业安全隐患[1]。若能控制或消除吊重摆角,可实现快速起重机小车精确定位,从而提高桥式起重机工作效率。PID控制是比例、积分和微分控制的简称[2]。近年来虽然许多先进控制方法不断推出,但PID控制器以其结构简单,对模型误差具有鲁棒性及易于操作等优点,广泛应用于冶金化工、电力、轻工和机械等工业过程控制中[3]。
PID参数整定方法有Ziegler-Nichols方法、幅值相位裕度设定方法、最优整定以及其它一些方法[4],但它们局限于线性系统。在Matlab NCD工具箱中提供专门的NCD Blockset用于非线性系统优化设计和仿真[5]。该工具箱以Simulink模块的形式,集成基于图形界面的非线性系统控制器优化设计和仿真功能。非线性规划是在一组等式和不等式约束条件下求一个函数极值问题。Matlab优化工具箱的函数constr.m是针对有约束条件的极值问题进行优化计算。它涉及KT(Kuhn-Tucker)方程的求解,BFGS(Broyden-Fletcher-Goldfarb-Shanno)[6]无约束变尺度法和 SQP(Sequential Quadratic Programming)[7]约束序列二次规划法。
针对桥式起重机在运行过程中会产生较大的惯性载荷,在启动和制动的过程中会导致负载摆动的问题,本文首先建立桥式起重机系统仿真模型,然后借助非线性控制系统优化设计的工具箱 NCD,快速实现桥式起重机防摆系统参数的优化设计。
1 桥式起重机数学模型建立
桥式起重机系统中,只有大车和小车在各自方向做水平移动,这两个方向上的运动是自然解耦的,要控制桥式起重机任意位置的防摆,只需要研究小车的运动即可,而大车的控制规律相同。桥式起重机小车运行系统模型如图1所示。

图1 桥式起重机简化模型
利用拉格朗日力学对系统进行受力分析可得[8]:

其中,M为小车质量;m为吊重质量;x为小车位移;F为小车驱动力,g为重力加速度;Fl为钢丝绳提升力;μ为轨道和小车之间的摩擦系数。
考虑到桥式起重机实际工作状况,为研究方便,钢丝绳长度变化忽略不计,即θ在0θ=附近变化较小,可以取sin0θ=,cos1θ=,则系统模型可以简化为:

由式(4)、式(5)联合式可得:

在 Simulink中建立桥式起重机系统仿真模型如图2所示。假设小车质量M = 5 kg,摩擦系数μ=1,输入参数u(1)、u(2)、u(3)、u(4)、u(5)分别代表x、F、m、l、θ,其中m、l为可调节参数。

图2 桥式起重机系统仿真模型图
2 NCD优化PID桥式起重机防摆仿真
将图2所示模型进行封装,以此为被控对象并引入小车位置PID控制器PID1作为外环控制,吊重摆角PID控制器PID2作为内环控制,分别对位置输出端和摆角输出端各添加一个NCD模块,结构如图3所示。

图3 桥式起重机PID双闭环控制结构图
取m=2,l=0.8。仿真程序包括2部分:Simulink程序及初始化的M函数程序。在Simulink中双击NCD Output模块,弹出NCD Block约束窗口,设置步骤如下:
1) 设置Step Response定义阶跃响应性能指标,参数定义如表1所示;

表1 Step Response定义阶跃响应性能指标
2) 设置 Parameters定义调整变量及参数如表 2所示;
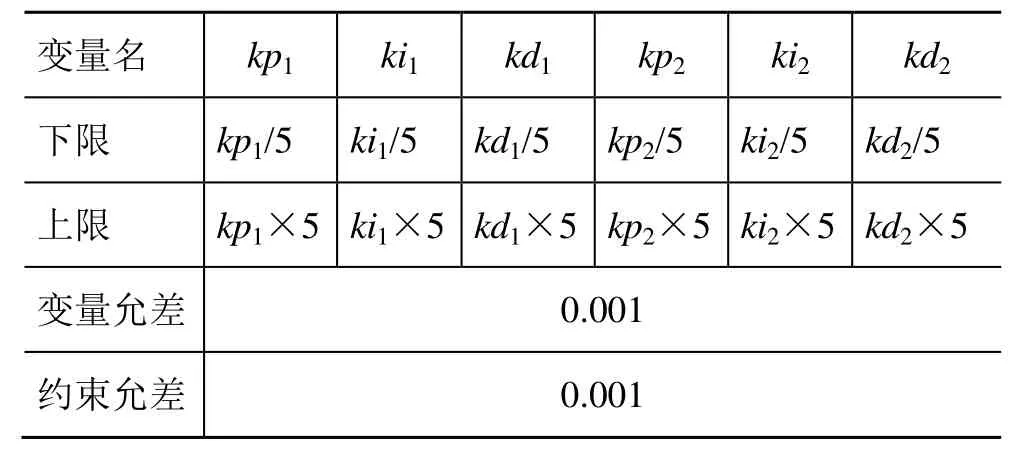
表2 Parameters定义调整变量及参数
3) 选择界面Start命令,进行调整变量的优化,直到阶跃响应指标达到要求为止。优化参数结果如表3所示。
将优化参数用于PID控制器,仿真得到小车位置x的响应如图4所示,吊重摆角θ响应如图5所示。可以看出,小车位置在5 s完成消摆并到达指定位置。

表3 PID优化参数结果
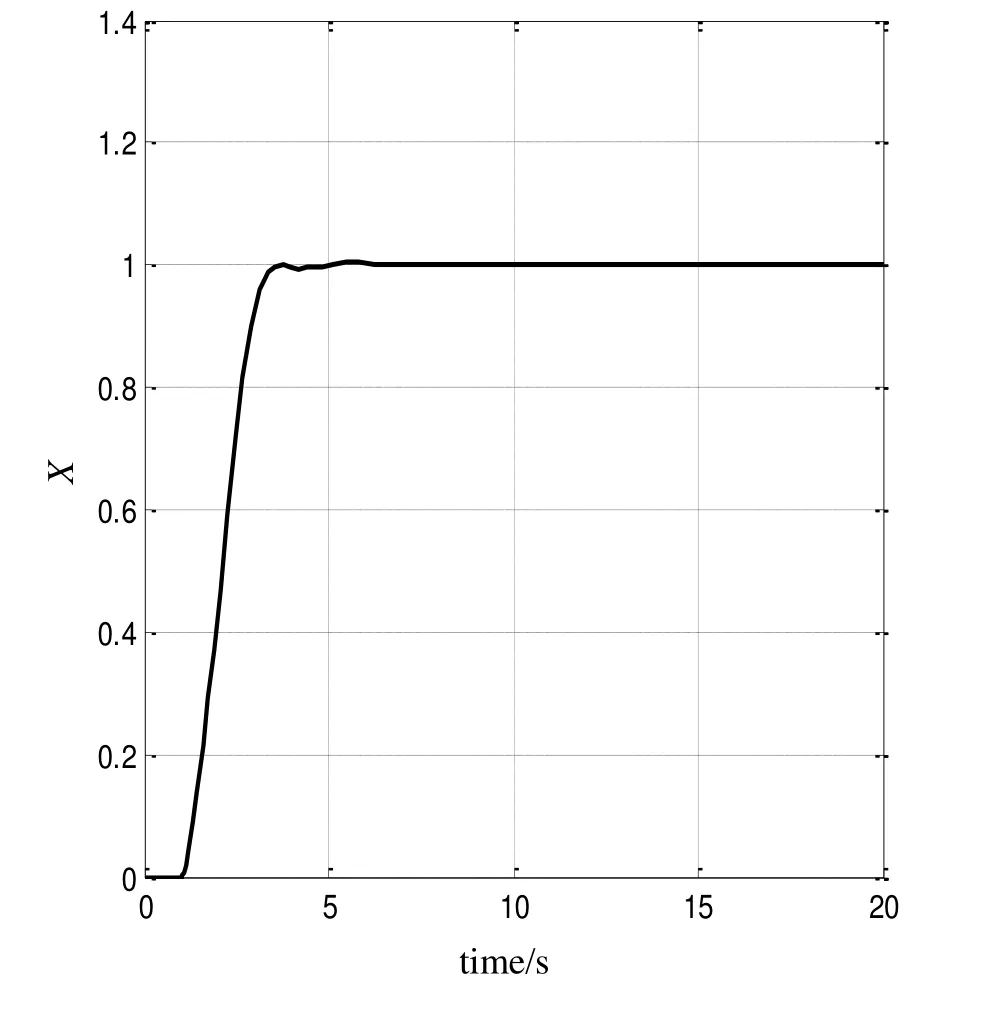
图4 小车位置x响应

图5 吊重摆角θ响应
3 NCD优化PID桥式起重机防摆系统鲁棒性验证
在图3桥式起重机PID双闭环结构中,将常量m=2,l=0.8改为变量,结构如图6所示。在NCD Block约束窗口中设置步骤如下:

图6 变参数桥式起重机PID双闭环控制结构图
步骤1)、步骤2)同2节;
3) 设置Uncertainty定义不确定变量及有关参数如表4所示;

表4 Uncertainty定义不确定变量及有关参数
4) 选择界面Start命令,进行调整变量的优化,直到阶跃响应指标达到要求为止。优化参数结果如表5所示。

表5 PID优化参数结果
取不同组m、l参数来验证所优化参数的鲁棒性:
1) 取m=2,l=0.7,小车位置x的响应如图7所示,吊重摆角θ响应如图8所示;

图7 取m=2、l=0.7时小车位置x响应

图8 取m=2、l=0.7时吊重摆角θ响应
2) 取m=3,l=0.6,小车位置x的响应如图9所示,吊重摆角θ响应如图10所示。
由仿真图可知小车在5 s左右到达目标位置,吊重摆角消除。可见即使在桥式起重机系统参数 m、l发生一定变化时,系统仍能快速消除摆动,达到满意的控制效果,优化后的PID参数对于系统参数的变化具有一定鲁棒性。
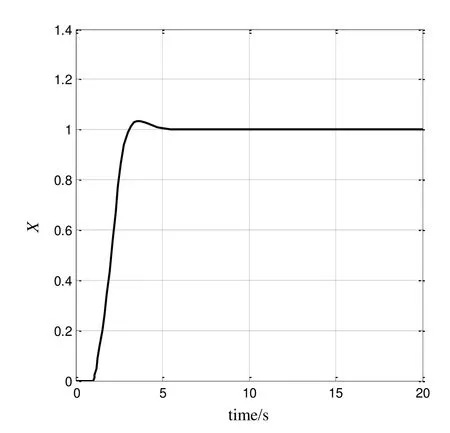
图9 取m=3、l=0.6时小车位置x响应

图10 取m=3、l=0.6时吊重摆角θ响应
4 结论
PID是工业控制中应用最普遍的一种控制规律,本文将NCD非线性优化PID控制方法应用在桥式起重机防摆控制系统中,避免了传统设计中复杂计算,快速精确得到所需控制参数。
通过设定桥式起重机容易变化参数的范围,使得在参数在一定的变化范围内,控制系统仍能达到满意的控制效果,具备一定鲁棒性。
[1] 王克奇.桥式起重机的定位和防摆控制研究[J].系统仿真学报,2007,19(8):1799-1802.
[2] 陶永华,尹怡欣,葛芦生.新型 PID 控制及其应用[M].北京:机械工业出版社,2002.
[3] 夏晓晶.单片机实现的仿人智能PID控制器[D].大连:大连海事大学,2004.
[4] 滕青芳.基于NCD工具箱的非线性系统PID控制器优化设计[J].电气传动自动化,2002,24(3):32-34.
[5] Math Works. MATLAB version 2 user’s guide [DB/OL].http://www.doc88.com/p-54805404.html.
[6] Fletcher R. A new approach to variable-metric algorithms[J].Computer Journal, 1970, 13(3): 317-322.
[7] Fletcher R. Practical methods of optimization[M]. Wiley, 1980.
[8] Ahmad M A, Raja Ismail R M T, Nasir A N K , et al.Anti-sway control of a gantry crane system based on feedback loop approaches[C].Singapore: IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 2009.

