π 尺的校准及其示值误差的测量不确定度评定

张 锐 冯凯飞 包 辉 毛建宏 高同山 齐梅梅

（1.河北省计量科学研究所，石家庄 050051；2.河北省计量监督检测院，石家庄 050051）

0 引言

π 尺是一种直径测量工具，主要用来现场测量任何材料圆、管、轴及滚筒等的平均直径。

随着π 尺的广泛应用，在计量方面对其采取合理的校准方法尤为重要，我们利用实验室现有的条件，借助钢卷尺检定台将π 尺与标准钢卷尺比较测量，方便快捷地实现了π 尺的校准，该方法切实可行，且能满足校准要求，从而保证了使用π 尺测量时的准确可靠。

1 π 尺的结构及使用方法

π 尺由一条弹性钢带构成，其两端分别刻有主尺和副尺。主尺的最小分度值为0.5mm或1mm，副尺的最小分度值一般有0.01mm、0.02mm、0.05mm等。π 尺按结构形式的不同主要分为条式、穿孔式和卷尺式。

使用π 尺测量时，只需将π 尺绕工件一周，用游标读数方法即可直接读出被测件的平均外径；测量内径时只须将π 尺翻过来使用后，读数值加上两个尺厚即可。π 尺是通过周长测得直径，可将生产时的刻线误差缩小π 倍后反映到测量结果上，所以在大直径测量中，其精度高于游标卡尺，且π 尺只需借助磁性桥、拉力器等附件就能实现单人精密测量，方便准确。

2 校准方法及实验数据

π 尺主要校准其长度尺寸，在实际校准过程中，借助于钢卷尺检定台利用标准钢卷尺就能满足校准需求，且大多实验室都具备这一条件，易于实现。

利用钢卷尺检定台来实现校准的具体过程为：用压紧装置将被校π 尺与标准钢卷尺紧固在测量平台上，分别在被校π 尺与标准钢卷尺的另一端施加各自规定的张紧力。测量时，调整测量平台上的调零机构，使被校π 尺的零值标记与标准钢卷尺的零值标记对齐，然后用读数显微镜分别瞄准被校π 尺标记范围内均匀分布的3 点和标准钢卷尺上对应的标记进行读数，并将π 尺标称值与标准钢卷尺相应读数的修正值进行比较。由于标准钢卷尺只在1m范围内每间隔100mm的位置上有上级校准机构给出的修正值，因此当被校π 尺的长度超过1m范围时，需将其调转方向，将其零值标记对准标准钢卷尺上相应的整数刻度，使标记刻度位于具有修正值的范围内再读数。当π 尺的长度大于检测台的长度时，可分段检测，用各段的实际长度之和计算示值误差。

使用π 尺测量时，其尺厚中性面的弯曲变形量最小，因此在设计刻度值时，以中性面为基准，但由于读数困难，刻度值标记在π 尺表面上，故计算其直径误差时，被校点的直径实测值需减去两个半尺厚，即一个尺厚，所以π 尺直径示值误差△为

式中，Di为π 尺被校点的直径标称值，mm；D0为π尺被校点的直径实测值，mm；L0为标准钢卷尺修正后的实际值，mm；h0为π 尺尺带的实测厚度，mm。

现以测量范围为50～300mm、分度值0.02mm、尺厚0.25mm的条式π 尺为例，在温度20℃，相对湿度50%，等温4 小时的条件下，取π尺标记范围内均匀分布的3 点进行试验，数据见表1。

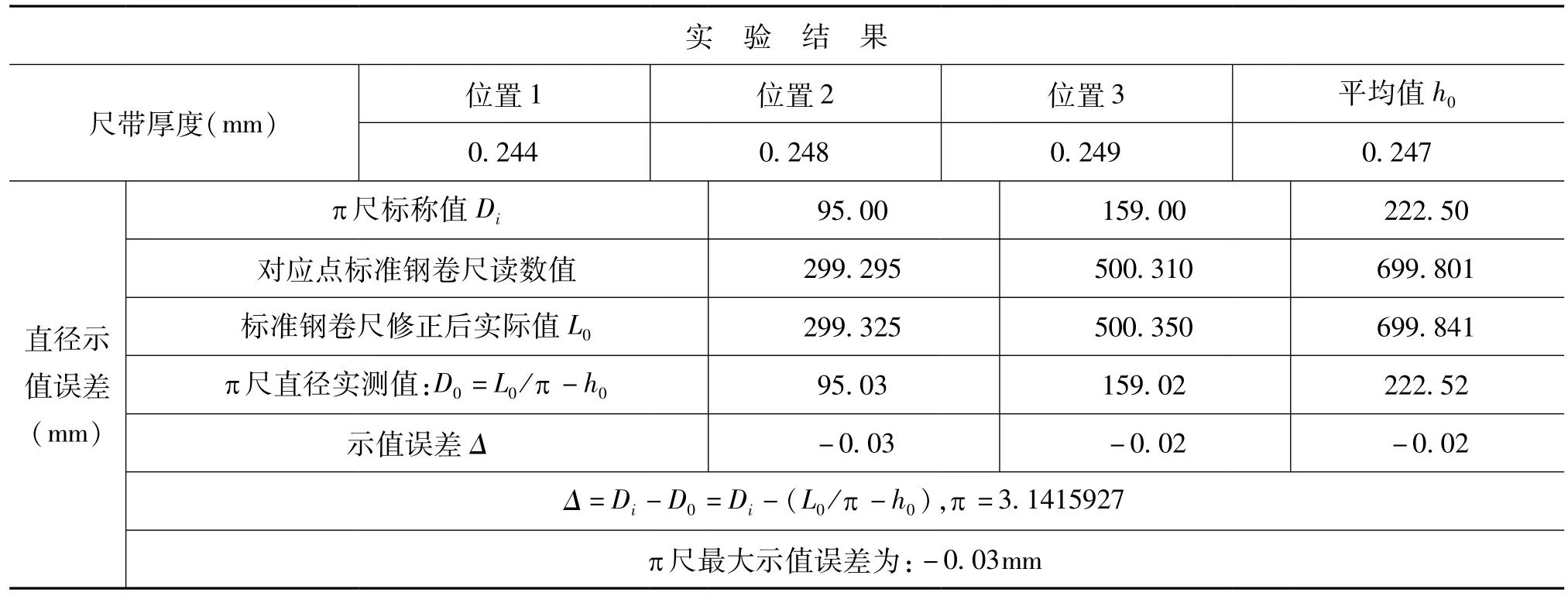
表1 50～300mm的π 尺实验结果

3 测量不确定度评定

3.1 数学模型

以表1 中的π 尺为例，分析其示值误差的测量不确定度，其标准不确定度分量见表2。π 尺示值误差的数学模型为

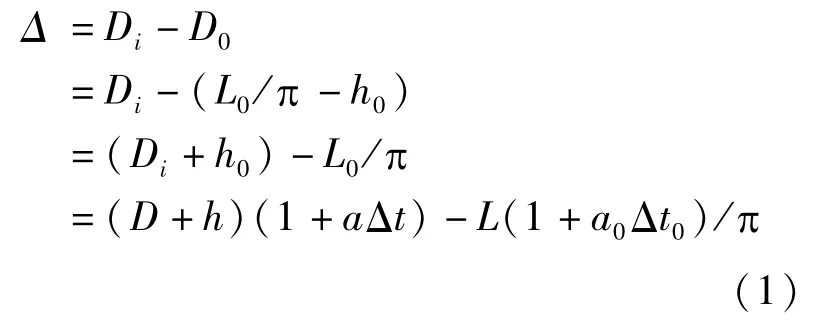
式中，D为π尺被校点的直径标称值（20℃条件下），mm；h 为π 尺尺带的实测厚度值（20℃条件下），mm；L 为被校点的长度实测值（20℃条件下），mm；a、a0分别为π 尺和标准钢卷尺的线膨胀系数，均为（11.5 ±1）×10-6℃-1；△t、△t0分别为π尺和标准钢卷尺偏离20℃′ 温度值；π＝3.1415927。

将上述参数带人式（1）并化简得

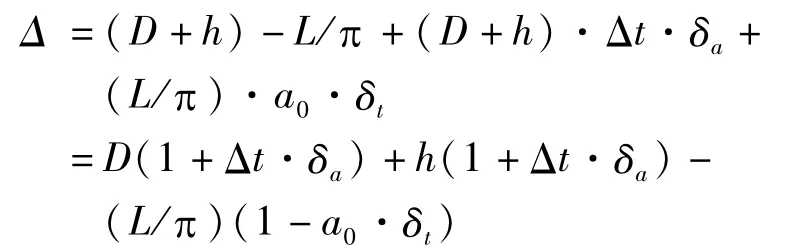
3.2 方差和灵敏系数

依据

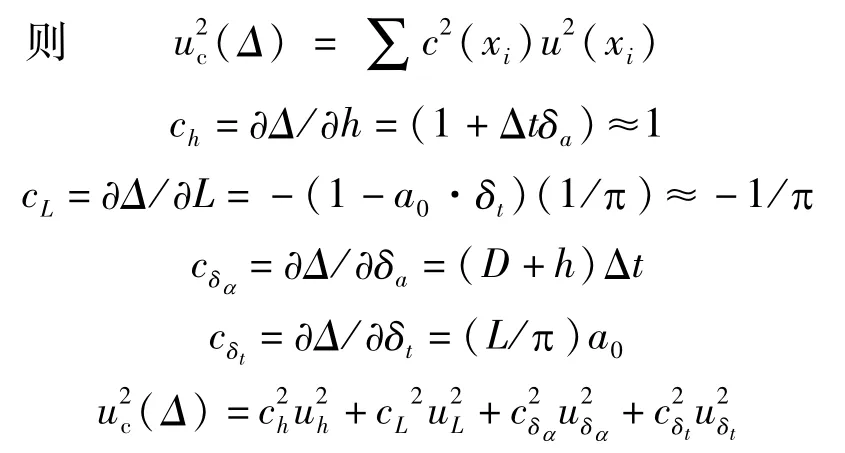
由于π 尺示值测量重复性或估读误差、读数显微镜示值误差和张紧力偏差都会引人不确定度，故输出量估计方差的完整表达式应为

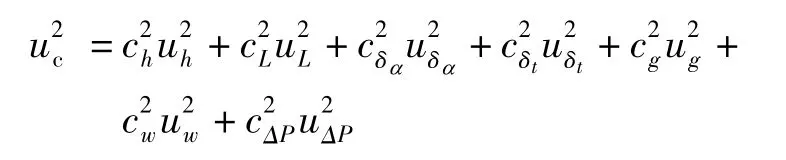
式中，ug为π 尺示值测量重复性或估读误差引人的标准不确定度分量；uw为读数显微镜示值误差引人的标准不确定度分量；u△P为由被校π 尺与标准钢卷尺的张紧力偏差引人的标准不确定度分量。

则

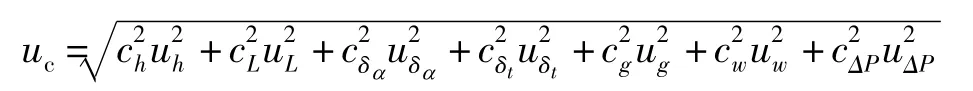
由于π 尺示值测量重复性或估读误差、读数显微镜示值误差对π 尺的影响是长度值的变化，除以π 才是对应直径的变化，故cg＝cw＝1/π。

3.3 标准不确定度分量计算

3.3.1 π 尺尺带厚度测量引人的标准不确定度分量uh

3.3.1.1 尺带厚度测量的重复性或量化误差引人的标准不确定度分量uh1

1）测量重复性引人的标准不确定度分量uh11

对π 尺某点，在重复性条件下用数显千分尺连续测量10 次，得到测量列（单位：mm）0.250、0.249、0.249、0.249、0.248、0.249、0.249、0.250、0.249、0.249，则

实验标准偏差

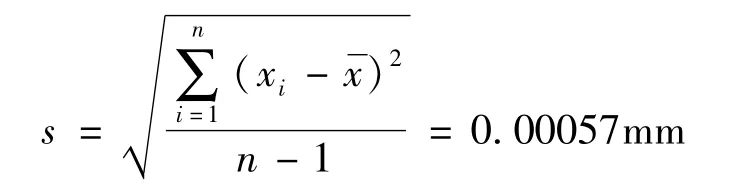
由于尺带厚度值是3 次测量的平均值，则

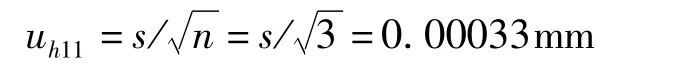
2）量化误差引人的标准不确定度分量uh12

分辨力为0.001mm的数显千分尺的量化误差为0.0005mm，均匀分布，k＝，则

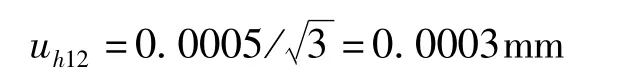
测量重复性和量化误差，两者中取较大值，故取：uh1＝uh11＝0.00033mm

3.3.1.2 千分尺示值误差引人的标准不确定度分量uh2

分辨力为0.001mm的数显千分尺的最大允许示值误差为±0.002mm，均匀分布，k＝，则

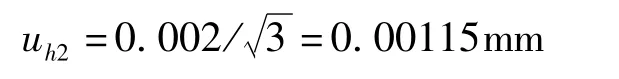
3.3.1.3 尺带厚度不均匀引人的标准不确定度分量uh3

由于尺带厚度不均匀而造成测量时引人误差，其最大差值不超过0.01mm，三角分布，k＝，则

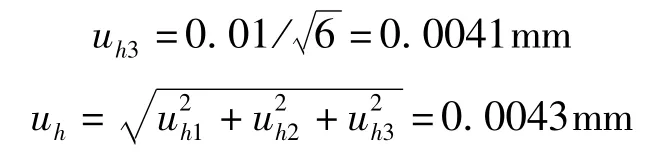
3.3.2 由标准钢卷尺引人的标准不确定度分量uL

3.3.2.1 由标准钢卷尺的测量不确定度引人的标准不确定度分量uL1

标准钢卷尺的测量不确定度为U＝（5 +5L）μm，（L单位：m），k＝2，取最大校准点L＝699.841mm≈0.7m，则

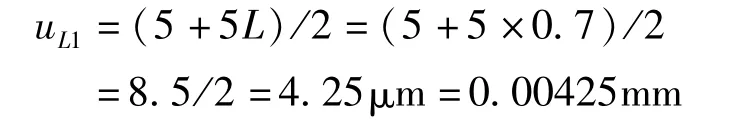
3.3.2.2 由标准钢卷尺的稳定性引人的标准不确定度分量uL2

标准钢卷尺的稳定性为0.01L mm，（L 单位：m），三角分布，k＝，则

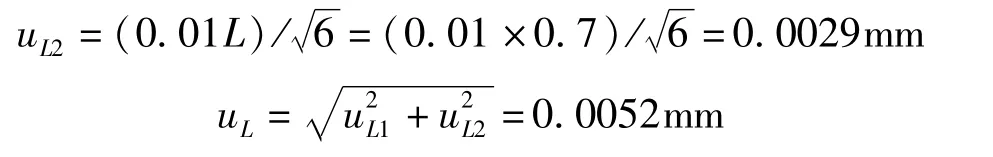
3.3.3 由被校π 尺与标准钢卷尺的线膨胀系数差引人的标准不确定度分量

被校π 尺与标准钢卷尺的线膨胀系数均为（11.5 ±1）×10-6℃-1，两者之差最大为2×10-6℃-1，三角分布，k＝，则

校准时，实验室温度偏离标准温度最大为△t＝5℃，由于尺带厚度值很小，20℃条件下的厚度值约等于（20 ±5）℃条件下的厚度值，即h≈0.25mm，则

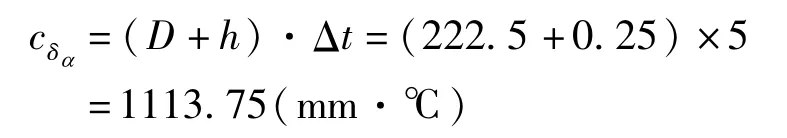
3.3.4 由被校π 尺与标准钢卷尺的温度差引人的标准不确定度分量

被校π 尺与标准钢卷尺的温度差估计为0.3℃，均匀分布，k＝，π 尺和标准钢卷尺的线膨胀系数均为11.5 ×10-6℃-1，则

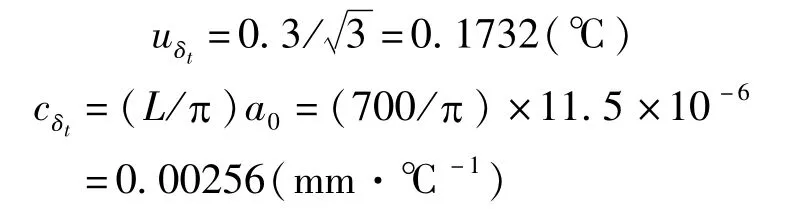
3.3.5 π 尺示值测量重复性或估读误差引人的标准不确定度分量ug

3.3.5.1 π 尺示值测量重复性引人的标准不确定度分量ug1

对π 尺某点示值，在重复性条件下用读数显微镜连续测量10 次，得到测量列（单位：mm）0.290、0.286、0.288、0.287、0.288、0.287、0.290、0.288、0.290、0.288，则

实验标准偏差

则 ug1＝s＝0.0014mm

3.3.5.2 π 尺示值测量时估读误差引人的标准不确定度分量ug2

π 尺示值测量时，用分度值为0.01mm的读数显微镜读数，其估读误差为0.001mm，均匀分布，k＝，则

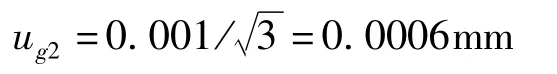
测量重复性和估读误差，两者中取较大值，故

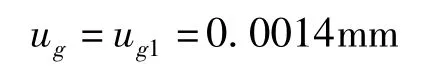
3.3.6 读数显微镜示值误差引人的标准不确定度分量uw

分度值为0.01mm的读数显微镜的最大允许示值误差为0.010mm，均匀分布，k＝，则uw＝0.010＝0.0058mm

3.3.7 由被校π 尺与标准钢卷尺的张紧力偏差引人的标准不确定度分量u△P

被测π 尺与标准钢卷尺张紧力的偏差均为0.5N，则两者最大差值为1N，均匀分布，k＝，则

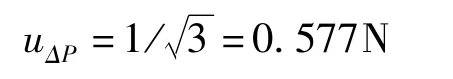
由张紧力偏差引起的变形量△L 对应的直径变化量△D为

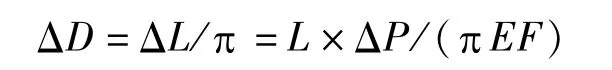
式中，△P为张紧力偏差，N；E为弹性系数，（21000×9.8）N/mm2；F为π 尺的横截面积，F＝3mm2。

由上式得

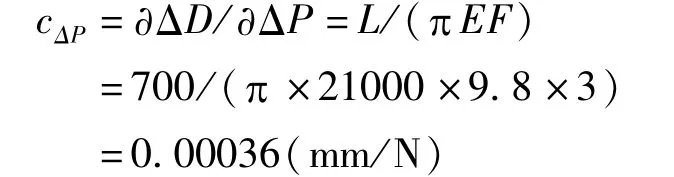
3.4 合成标准不确定度uc

3.5 扩展不确定度U

取k＝2，则U＝k×uc＝2 ×0.0051mm≈0.01mm。

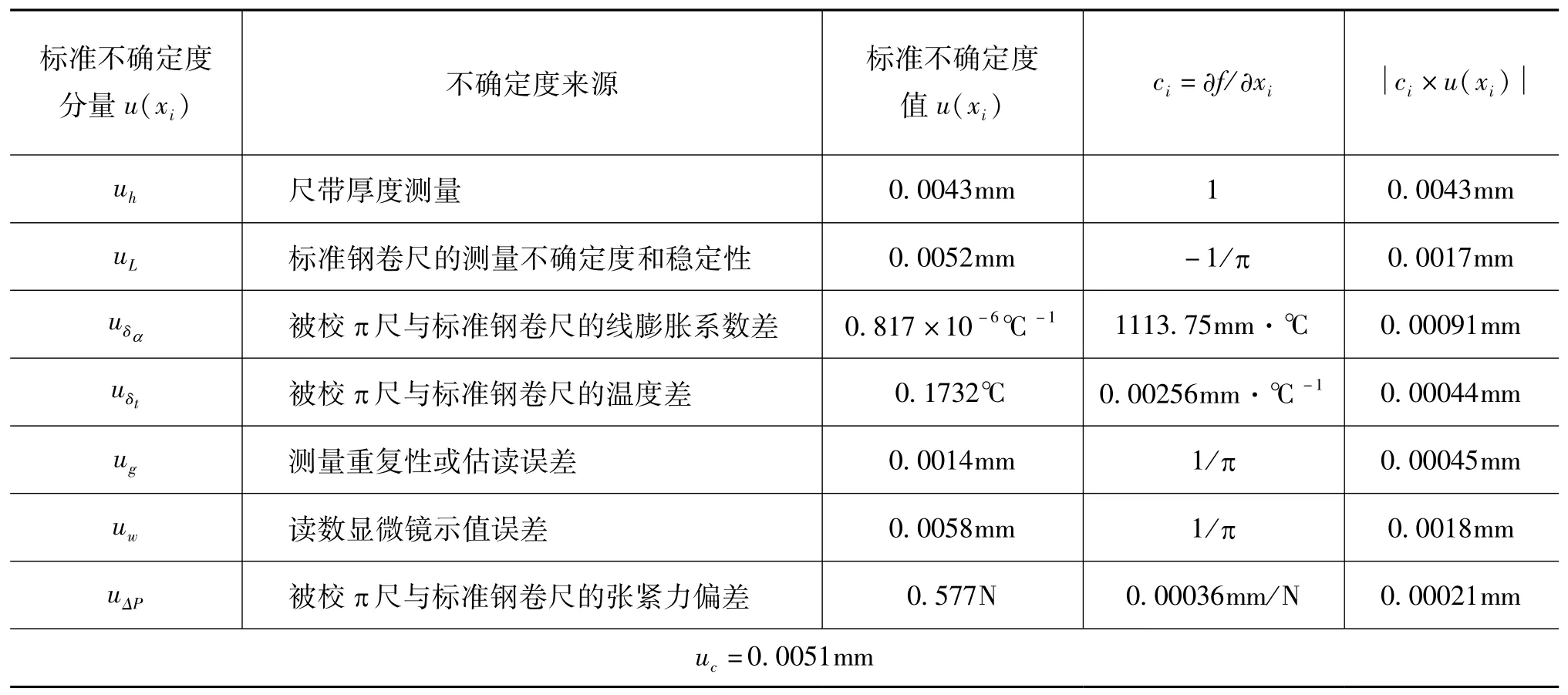
表2 50～300mm的π 尺示值误差不确定度分量

4 结束语

通过以上分析可知，对于50～300mm的π 尺，U＝0.01mm，由生产π 尺的企业标准可知此范围π 尺的MPEV＝0.05mm，故以上校准方法完全满足需要，且大多实验室都具备这一条件，切实可行。另外也可以用激光干涉仪、母尺等满足测量不确定度要求的其他标准器进行校准。