两轮机器人在坡面上的运动平衡控制*

阮晓钢， 李亚磊， 朱晓庆

(北京工业大学 人工智能与机器人研究所, 北京 100124)

0 引 言

两轮机器人是自平衡机器人家族中的一员，两轮机器人的平衡问题类似于倒立摆的平衡问题，不同的是,倒立摆只能在二维空间中运动，而两轮机器人是可以在三维空间中运动。目前，关于两轮机器人的运动控制研究，大多是在平面上的运动控制，在坡面上运动的两轮机器人由于受到重力的影响，其平衡控制变得更为复杂。

2002年，瑞士联邦工业大学的Grasser F[1]通过解耦分解运动简化了两轮机器人的控制，研制出可以实现自平衡的两轮机器人Joe，Joe能够稳定地做U型回转和零半径回转。2003年，美国南卫理工会大学的Anderson教授制作了两轮机器人nBot，nBot采用基于状态反馈的控制方法，具有鲁棒的运动平衡控制性能，能在崎岖道路行进，但是不具备自主起立的功能。北京理工大学的李航、河南科技大学的韩建海和赵书尚等人[2～4]，通过极点配置方法设计了闭环状态反馈控制器，实现了两轮机器人在平面上的平衡控制。2006年，韩国的Kim Y[5]运用牛顿力学的方法建立了两轮机器人在平面上的动力学模型，对两轮机器人在斜坡上的运动进行了分析讨论，但是并没有给出斜坡上适用的数学模型。2010年，北京工业大学的李欣源等人[6]成功研制出具有柔性腰椎的柔性两轮自平衡机器人“原人”，提出了一种基于非线性PD的三环控制方法来控制两轮机器人在平面上的姿态平衡和运动控制，其控制能力达到了国际领先水平。

本文首先利用拉格朗日方程方法建立了两轮机器人在坡面上的动力学模型，然后设计了一种非线性PD控制器控制两轮机器人在坡面上的姿态平衡。与传统的线性PD控制器进行多项仿真实验对比，在动态性能、鲁棒性方面，非线性PD控制器有着更好的控制效果，最后加入速度控制，与姿态控制构成双环的PD控制，实现了两轮机器人在坡面上的静态平衡。

1 两轮机器人在坡面上的动力学建模

两轮机器人在坡面上运动时，由于受到重力作用的影响，两轮机器人的平衡控制变得更为复杂。每个控制任务本身就是一个动力学任务，本文利用Lagrange方程方法，以能量方式建立两轮机器人在坡面上的动力学模型。建模的假设条件[7]：

1)两轮机器人的车轮直径相等；

2)机器人的机身、车轮均为刚体；

3)两轮机器人在坡面上运动时，车轮只有滚动没有滑动；

4)忽略传感器噪声。

以机器人两轮轮轴中心为原点建立笛卡尔直角坐标系，如图1所示，x轴为两轮机器人沿着坡面的前进方向，y轴与两轮轴线方向一致，且以指向左轮轴心的方向为正，z轴为垂直斜坡向上。大地坐标系为X1，Y1，Z1。

图1 机器人系统的受力分析图

表1中列出了机器人动力学建模的参数定义。

表1 两轮机器人的参数定义

拉格朗日方程公式为

(1)

其中，L=T-U，为拉格朗日算子，T为系统的总动能，U为系统的总势能，D为耗散能,qs为系统的广义坐标，定义系统的广义坐标为qs=[q1,q2,q3]T=[θb,φl,φr]T，Qs为广义力。

通过运动学关系推导可以得到:

1)系统动能

(2)

2)系统势能

U=MgLcosθb.

(3)

3)系统耗散能

(4)

4)系统的广义力

(5)

引入电机模型

(6)

带入方程(1)得到一个二阶非线性微分方程，即为两轮机器人在坡面上的动力学方程

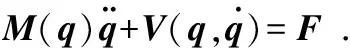
(7)

其中

cosθbcos2θcosθs-cosθsinθbsinθs)

n1=-MgLsinθb-M2L2sinθbcosθb+2μwb-

sinθbcos2θcosθs+cosθbsinθscosθ),

sinθbcos2θcosθs+cosθbsinθscosθ),

sinθbcos2θcosθs+cosθbsinθscosθ),

2 非线性PD控制器设计

两轮机器人主要通过陀螺仪和倾角仪检测实时的姿态，不可避免地有噪声信号，这些信号经过积分环节随时间累积，反而会增大静态误差而影响控制效果，所以，选择控制器为PD控制，而非PID控制。

根据控制原理的不同，非线性PID控制器可分为两类[8]：直接控制量(direct-action)型和增益调整(gain-sche-duling)型。数学表达式分别为直接控制量型

u(DA)=uP(x,θP)+uI(x,θI)+uD(x,θD).

(8)

增益调整型

(9)

其中，u,e分别为控制量输入与控制响应误差信号；x,θ分别为非线性函数的自变量向量与参数向量；uP(·),uI(·),uD(·)分别代表比例、积分、微分3个非线性分量函数，而KP(·),KI(·),KD(·)分别代表比例、积分、微分3个非线性增益函数。

两轮机器人的控制量是两轮电机的输入电压，当e=0，输入电压为0；当e=maxe，输入电压为电机最大值；结合文献[3]中分析关于比例控制分量uP(·)方面的先验知识充分，本文选择如式(8)的直接控制量型非线性PID控制器，构造一种PD控制器，具体形式为

τB=PDNLB(θb)=KP(θb)+KD(b)

(10)

3 仿真实验

在Matlab环境中，基于S函数方法，建立两轮机器人在坡面上的Simulink控制模型如图2所示。

图2 两轮机器人在坡面上的Simulink模型

3.1 姿态平衡控制实验

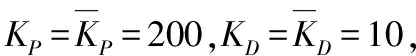
图3 两轮机器人在坡面上的自平衡仿真实验

实验结果可见，两轮机器人在坡面上运动时，线性PD控制器和非线性PD控制器都可以实现姿态的平衡控制，不过线性PD控制器在机身倾角小角度时候反应不够灵敏，达到稳定状态需要时间长，非线性PD控制器有更好的快速性和稳定性。另外,从实验中可以看出机器人最后的倾角都没有到达0°，因为控制器中没有加入速度控制环，所以,机器人会提供一定的机身倾角，保持在坡面上的匀速运动状态。

3.2 鲁棒性实验

在相同初始条件下，姿态平衡控制的过程中，加入脉冲扰动，阶跃扰动和随机噪声，分别对线性PD和非线性PD控制器进行仿真实验，测试2种控制器的鲁棒性。

3.2.1 脉冲干扰实验

在3 s时对机身加入持续时间1 s、幅值为5的脉冲扰动，分别对2种控制器进行实验，结果如图4所示。

图4 脉冲扰动时两轮机器人的姿态控制

从图4中可以看出，两轮机器人机身在受到脉冲扰动时，非线性PD控制器能更好的控制机器人机身的平衡，受到脉冲的影响较小。

3.2.2 阶跃干扰实验

在3 s时，对机器人机身加入幅值为20的阶跃扰动(图5)，实验结果说明:线性PD控制器已经不能有效地控制机器人机身的平衡，机身倾角开始发散，控制失败。非线性PD控制器仍然能够控制机器人机身的近似平衡，有效地抑制了阶跃干扰，得到很好的控制效果。

图5 阶跃扰动时两轮机器人的姿态平衡控制

3.2.3 随机噪声实验

在获得的机器人机身倾角数据加上周期为2 s，最大值为1°的正弦噪声信号，得到控制结果如图6所示。

图6 加入随机噪声时两轮机器人的姿态平衡控制

线性PD控制器下的两轮机器人由于噪声作用，机身倾角也随着振荡，控制效果不佳。而非线性PD控制器能够很好的过滤噪声，受到的影响很小，仍然可以保持机器人的机身平衡。

3.3 静态平衡控制实验

与在平面上运动不同，两轮机器人在坡面上运动时，不加速度控制环节，只能保持匀速运动下的平衡，不能保持静态平衡。所以,有必要在姿态平衡的控制同时加入速度控制环，构成双环控制，才可以让机器人在坡面上保持静态平衡。

对非线性PD姿态控制器，加入速度控制环节后，得到实验结果如图7所示

图7 两轮机器人在坡面上的静态平衡控制

在加入速度控制环节后，两轮机器人在坡面上的倾角和轮子转速都可以等于0。以姿态平衡为主，速度控制为辅的双环PD控制下，两轮机器人在坡面上实现了静态平衡。

4 结束语

本文分析两轮机器人在斜坡上的受力情况，利用拉格朗日方法建立了两轮机器人在坡面上的动力学模型，基于模型在Matlab中搭建仿真环境，分别设计了两轮机器人姿态平衡的线性PD和非线性PD控制器，通过仿真实验，验证了非线性PD控制器相比线性PD控制器，有更好的动态性能和鲁棒性。最后结合姿态平衡控制器加入速度控制环节，实现两轮机器人在坡面上的静态平衡。

参考文献:

[1] Grasser F,D’Arrigo A,Colombi S.JOE:A mobile inverted pendulum[J].IEEE Trans on Industrial Electronics,2002,49(1):107-114.

[2] 李 航,孙厚芳,韩建海,等.两轮机器人行走机构的建模与实验[J].北京理工大学学报,2004,24(12):1058-1061.

[3] 韩建海,李 航,白玉川,等.平行双轮电动车的建模与控制仿真[J].中国机械工程,2005,16(8):683-686.

[4] 赵书尚,韩建海,李济顺,等.平行双轮电动车及其控制系统的研究[J].机电工程,2005,22(1):12-15.

[5] KimY,Kim S H,Kwak Y K.Dynamic analysis of a nonholonomic two-wheeled inverted pendulum robot[J].Journal of Intelligent and Robotic Systems,2005,44:25-46.

[6] 李欣源,阮晓钢,任红格.柔性双轮机器人建模与分析[J].机器人,2010,32(1):138-144.

[7] 王晓宇.两轮自平衡机器人的研究[D].哈尔滨：哈尔滨工业大学，2009:2-26.

[8] 胡包钢.非线性PID控制器研究—比例分量的非线性方法[J].自动化学报，2006,32(2):219-227.