基于无线传感器网络的同时定位与跟踪*

赵亚凤, 任洪娥

(东北林业大学，黑龙江 哈尔滨 150040)

0 引 言

无线传感器网络一个很重要的应用就是敌方军事目标检测与跟踪。另外，无线传感器网络在民用方面也有很多的应用，如生态环境监测、智能交通控制、基础设施安全、微创医疗装置等，都用来跟踪不同的目标，确定其位置信息。在这些应用中，需要在预定区域随机散播大量无线传感器节点组成无线传感器网络，实时跟踪目标位置信息。

移动目标跟踪时，需要精准的位置信息作为参考。而无线传感器网络的定位，由于其通常需要较大规模，能确定精确位置的人工部署不切实际；GPS虽能准确定位，但需要在节点配置相应设备，不符合传感器网络的小型化和成本要求。因此，低成本、高精度地准确跟踪移动目标，同时确定传感器网络节点位置是一种最好的解决方法。

目前，为了解决传感器网络的定位和移动目标的跟踪问题，一些文献提出了相关算法，文献[1～4]中使用一个移动的目标(或机器人)来定位无线传感器网络，因为它们不需要在节点上配置额外的硬件资源，是一个很好的解决方案，但这些方法需要在任何时候都知道运动物体的位置，不符合目标跟踪的需求。有一些文献使用传感器网络跟踪移动目标[5]，这些方法假定传感器网络节点位置信息是确定的，适用于小规模传感器网络，对网络定位能力提出了较高的要求。本文根据同时定位与构图(SLAM)的相关理论，研究一种同步定位与跟踪算法，跟踪一个不确定的运动物体位置，同时定位和校准传感器网络的节点位置信息。

1 同时定位与跟踪原理

移动目标在一个粗定位的环境地图中确定自己的位置，同时根据新的测量信息校正地图,在过去的十多年中，SLAM方法证实了处理这类问题的有效性。利用SLAM的思想，在线估计与更新移动目标的位置并更新传感器网络节点位置。

由于接收信号强度指示 (received signal strength indication，RSSI) 的定位技术利用能量的测量可直接计算节点间距离，没有常用的视觉传感器的视线障碍，但距离估计的可靠性不高。本文在初始估计时，允许有一定误差存在，选用RSSI测量确定节点对和节点与目标的相对距离。本文利用多维定标(multidimensional sealing，MDS)的思想，根据经典计量多维技术得到每个节点的一跳邻居节点相对坐标图，依次传播得到网络的相对坐标图，即根据节点和节点间的相关性信息来确定未知位置的节点坐标。

本文假设目标可以随意移动，传感器节点位置固定，移动目标与节点间能相互通信。首先，利用传感器网络节点对之间的距离信息，对传感器网络初始定位。但这些定位信息通常包含很大的误差，不能作为目标跟踪的绝对参考，需要根据目标在行进过程中与节点的相对距离，实时更新节点位置，同时跟踪目标。为了实现这一过程，基于Kalman滤波的理论得到广泛研究，但随着目标前进，测量信息增加，滤波器状态方程维数随之增大，产生很大的计算量，不适合无线传感器网络节点的分布式计算。本文利用Kalman滤波的可取特点，使用压缩Kalman滤波估计与更新减小算法复杂度，实现分布式算法的实时性要求,算法原理如图1所示。

图1 同时定位与跟踪的基本原理

2 算法分析

2.1 利用MDS的传感器网络粗定位

在所有节点间实际几何距离正确的情况下,经典的MDS算法可以给出没有误差的解。但是,由于节点的通信范围限制,几乎不可能实现所有网络节点间的精确测距。在实际应用中,只能测量相邻节点间的距离信息,而对于多跳节点间的距离,本文利用Euclidean算法计算节点间几何距离[6]。

首先,计算所有节点间的距离,建立MDS所需节点的距离矩阵D(X),再对距离的平方所构成的矩阵D2(X)双重中心化,然后对双重中心化后的矩阵进行奇异值分解,最后计算出所有点的相对坐标X，生成相对坐标图,并利用少量的信标节点和坐标的旋转、平移将全局相对坐标转换成绝对坐标。只需知道3对转换前后的二维坐标，实现最优线性转换。

2.2 系统动态模型和观测模型

利用MDS算法，可以获得网络中节点的位置信息，第i只传感器节点的位置描述为pi=(xi,yi)，考虑到所有节点是固定不动的，第i个节点的状态转移方程为

pi(k)=pi(k-1)=pi.

假设系统中有效的节点数为N，用向量表示为

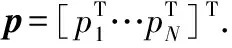
移动目标的状态用xv(k) 给定，构成系统状态的有移动目标状态和传感器节点的位置状态，称为扩张的状态向量,表示为

扩张的状态转移模型可完整描述为

X(k)=A(k)X(k-1)+V(k-1),

式中A(k)为状态矩阵，V(k)用于表示系统动态噪声。可见，矩阵的维数为n×N，n为与每个节点关联的状态量，N为组合成地图的节点个数。在一个大的环境中，外部传感器不断获得测量数据，构成环境地图的路标数不断增加，矩阵维数呈几何数量增长，给计算机造成很大负担。

移动目标和传感器节点同样配置,利用RSSI技术获得节点和目标之间的相对定位,第i个节点的观测模型可写为

Z(k)=H(k)X(k)+W(k),

式中W(k)用于表示系统测量误差，该向量为一个零均值，方差为Ri(k)的随机向量;Hi为观测的第i个节点相对于系统状态的观测矩阵。

2.3 滤波算法分析

Kalman滤波包括2个阶段：估计和更新。在估计阶段，滤波器利用上一时刻的状态估计当前状态，更新阶段，滤波器利用在当前状态的观测值优化预测阶段的预测值，以获得一个更精确的当前状态的估计。

在经典SLAM算法中，状态向量维数为移动目标状态加节点数的2倍，即M=2N+3，而在实际的目标跟踪中，只有移动目标周围一跳内的节点是有意义的，大量节点位置信息并无参考价值[7]。经典算法中随着节点数目的增加，标准滤波计算量剧增，不适用于实时目标跟踪。本文提出压缩滤波来减小实时计算,将复杂度减小到O(2Na2)，Na是局部区域的路标数。

在压缩EKF滤波中，将状态分为2个部分

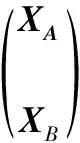
XA∈R2NA+3,XB∈R2NB,N=NA+NB.

状态XA被定为移动目标周围一跳内的节点状态，移动目标的状态也包括在XA中。假设在一段时间内得到的观测点只与状态XA相关，与XB不相关，即

h(x)=h(XA),H=[HA0].

根据2种不同的状态，误差协方差矩阵P写为

考虑时刻k,更新之后的协方差矩阵为

P(k|k)=P(k|k-1)-ΔP,

在目标跟踪任务中，XA状态维数将会通常比全局地图的总维数小很多，即NA≪NB≪M，矩阵μ(k),ξ(k)为稀疏的,压缩的滤波算法会使得算法复杂度得到很大程度降低。

3 仿真结果

由于RSSI定位距离超过20 m时有较大误差，将传感器最大测量距离定为20 m。在长、宽均为180 m的范围内，随机布置的节点个数为80个，设置3个配备GPS的锚节点。利用MDS算法对网络节点初始定位如图2所示，节点平均误差为5 m。本文利用一种简便的方法划分全局地图，将全局地图分为9个正方形，每个正方形边长为60 m，选择边长为60 m的正方形作为局部区域。

如果移动目标和探测到的节点属于同一个封闭区域，不会产生较大误差，但在探测到相邻区域的节点时，由于前面节点的相关信息丢弃，会使得节点的估计位置误差变大， 同时改变节点所在的区域的定位误差。本文在局部区域转换时设置一个滞后区域来避免多重地图切换产生的误差，即地图之间有一定的重合，将该重合区域设定为20 m，如图2中虚线所示。图中圆圈为估计位置,黑圆点为实际位置，黑色方框为锚节点，中间连线表示误差。

图2 压缩滤波算法的地图处理

在图2所示的传感器节点布局中，移动目标从原点开始随机移动，移动速度为1 m/s，线速度标准差为0.1 m/s，角速度标准差为3.00。设置实验中的观测参数，最大观测距离为20 m；观测时间间隔为0.2 s；观测的距离标准差为0.1 m。短距离和长距离的目标跟踪和传感器节点定位如图3和图4所示。

图中“*”号描述实际节点位置，“+”号表示估计节点位置，椭圆表示估计误差，“-”表示估计移动路径，“·-”表示实际移动路径，可见在较短距离的目跟踪任务中，误差会越来越大。在长距离的跟踪任务，由于关联到确定位置的节点，误差会随着路径的增加而减小。

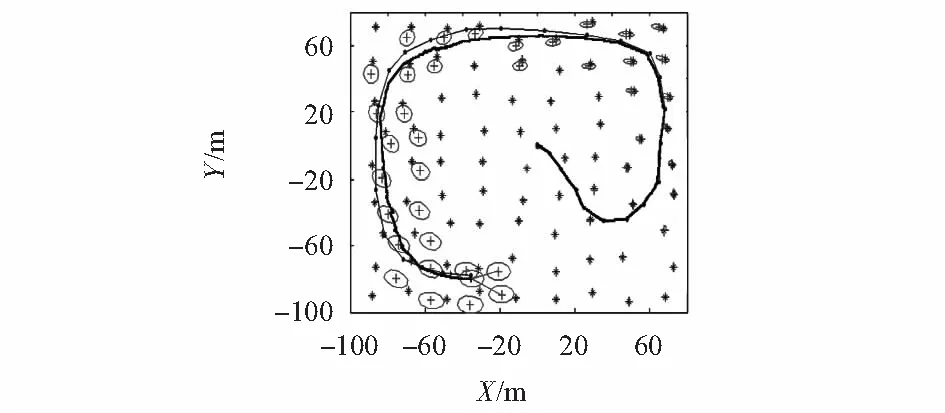
图3 短距离目标跟踪

图4 长距离目标跟踪

经典EKF滤波算法中，80个参考节点的目标跟踪，算法复杂度为O(812)。本文中所用压缩滤波算法计算量为O(Na2)，在离开本地区域时更新的复杂度是O(Na2Nb2)。每个区域内节点个数小于10，区域内算法复杂度最大为O(102)。移动到一个新的区域时，需要做一个全局的更新，但该算法复杂度也远小于经典EKF。

在经典的目标跟踪任务中,传感器节点位置误差在初始定位后保持不变,本文的算法节点位置误差随时间变化比较如图5所示。

图5 WSNs节点定位误差比较

实线为经典MDS定位后的WSNs节点误差协方差矩阵行列式,虚线为同时定位与跟踪的节点误差协方差。可见，在短距离的跟踪中，节点误差没有得到很好的改善，随着关联节点的增多，节点误差随着跟踪的进行而减小。

图6为重复实验中目标跟踪误差取均值的结果。实验结果表明:多次实验的平均误差在0.9～2.6 m间，可见算法有较高的精度和稳定性。

图6 多次跟踪平均误差

4 结 论

本文提出了无线传感器网络节点位置不确定时移动目标的跟踪和节点位置的更新。仿真结果表明:该算法能减小无线传感器网络节点的位置误差，在初始位置节点位置为5 m的情况下，通过估计—更新步骤，将节点平均位置误差降低到3 m以下。同时，目标跟踪的误差最大为2.6 m，并很大幅度减小算法复杂度。尤其是长距离的跟踪任务中，经典EKF滤波算法复杂度太高而不能满足实时性的要求，本文用一个局部SLAM算法的代价完成载体位置和局部地图中的地标位置估计，体现了该算法在长时间执行的优越性。

参考文献:

[1] Pathirana P,Bulusu N,Ha S J,et al.Node localization using mobile robots in delay-tolerant sensor networks[J].IEEE Transactions on Mobile Computing,2005,4(4):285-296.

[2] Galstyan A,Krishnamaehari B,Lerman K,et al.Distributed online localization in sensor networks using a moving target[C]∥Proc of the Third International Symposium on Information,Wa-shington:IEEE,2004:61-70.

[3] Menegatti,Zanella A,Zilli S,et al.Range-only SLAM with a mobile robot and a wireless sensor networks[C]∥Proceedings of the 2009 IEEE International Conference on Robotics and Automation，Kobe,Japan,2009:1699-1705.

[4] Djugash Joseph,Singh Sanjiv,Kantor George A,et al.Range-only SLAM for robots operating cooperatively with sensor networks[C]∥IEEE International Conference on Robotics and Automation,2006:2078-2084.

[5] 姚先连,胡 贞,吕晓玲.无线传感器网络中卡尔曼滤波在移动目标跟踪中的研究[J].长春理工大学学报:自然科学版，2011，34(3):88-92.

[6] 王 健,赵亚凤,刘劲风.一种适用于大规模无线传感器网络的定位算法[J].东北林业大学学报,2009,37(8):84-89.

[7] Nebot E.Simultaneous localization and mapping 2002 summerschool[EB/OL].[2002—08—05].http：∥acfr.usyd.edu.au /home pages/academic/enebot/.