直升机吊舱姿态变化对电磁场测量的影响规律及其校正方法研究

曲昕馨，李桐林，王飞

吉林大学地球探测科学与技术学院，长春 130026

1 引言

航空电磁法是在地面电磁法原理基础上发展起来的一种空中测量的电磁法.1950年在加拿大开始生产飞行，目前已经发展成为一种常用的普查找矿和地质填图方法.航空电磁系统可归结为硬架系统和非硬架吊舱系统两种.其中吊舱系统是将发射和接收线圈固定在直升机后的吊舱中，吊舱由拖曳电缆与直升机相连.直升机电磁（HEM）吊舱系统具有较高的分辨率，非常适合于浅层地质填图及环境与工程问题（Fraser，1981；Huang and Fraser，2000；Huang and Fraser，2002；Yin and Fraser，2002；Yin and Hodges，2003）.直升机吊舱的姿态变化是指沿直线水平飞行的吊舱在受到外力的作用下所发生的旋转和倾斜.这些偏差改变了吊舱内线圈的方位，进而改变了线圈和地面之间的电磁耦合，使接收线圈处接收到的电磁响应较之正常飞行时产生了误差.因此，研究吊舱姿态变化对电磁响应的影响以及对姿态变化后的电磁响应进行校正具有很重要的意义.

对航空电磁系统吊舱姿态变化的研究始于20世纪80年代.Son（1985）研究了一种单一吊舱旋转对于有限收发距的垂直共轴、水平共面和垂直共面线圈系的电磁响应影响.Holladay等（1997）发现在使用航空电磁法进行海冰探测时，由于探头姿态的变化而发生探头飞行高度的变化，并影响到对海冰深度的反演，通过对高度的校正，获得了高精度的海冰厚度.Fitterman（1998）基于前人的研究成果，总结出吊舱姿态的变化对探测数据的影响包括两个方面，即高程的测量误差和收发线圈相对于地下介质的几何关系的变化.Reid等（2003）将姿态校正应用到船载电磁系统的南极洲海冰厚度探测中.Yin和Fraser（2004）研究了重叠偶极模型（即零收发距）直升机航空电磁系统的姿态校正.Fitterman和Yin（2004）对收发一体的航空电磁系统校正方法进行了拓展，并应用于频率域航空电磁探测.Kratzer和Vrbancich（2006）对由于吊舱发生钟摆状摆动所引起的激光测高仪误差进行了校正.Davis等（2006）又从直升机和吊舱的相互关系出发，研究了吊舱测量过程中的姿态变化，进行更加精确的校正.

本文首先推导出吊舱发生姿态变化后新的线圈系位置和磁偶极矩空间分量，并给出相应的计算公式.接着，用数值模拟的方法计算了五种模型参数下吊舱姿态变化前后三种线圈系的电磁响应比值.然后，将吊舱的姿态变化分解成两个单独的过程：即方向变化和位置变化，并分别讨论了两种单独变化对于总姿态变化电磁响应比的贡献.在此基础上，分别推导出方向变化和位置变化的校正因子，并近似认为总姿态变化校正因子与这两种单独变化校正因子的乘积成一定比例.最后分别使用Yin和Fraser（2004）提出的重叠偶极校正方法和本文提出的总校正方法对五种模型参数的合成数据进行了校正，通过对比发现相比于重叠偶极校正方法，使用总校正方法能得到更精确的校正结果.

2 线圈系的排列方式和吊舱的姿态变化

2.1 线圈系的排列方式

目前频率域直升机电磁系统常用的线圈系有三种，分别是水平共面线圈系（HCP）、垂直共面线圈系（VCP）和垂直同轴线圈系（VCX）（见图1）.其中HCP和VCX是最常用的线圈系，主要应用于地质填图；而VCP线圈系可以看作是HCP线圈系绕着它的长轴旋转90°得到的，并且在电性各向异性的应用中具有显著优势（Yin and Fraser，2002）.

图1 三种线圈系（HCP，VCP和VCX）在xz面内的投影示意图Fig.1 Sketch of projection in the xz-plane of three coil configurations（HCP，VCP and VCX）

2.2 吊舱的姿态变化

为了研究吊舱的姿态变化，需首先引入两种坐标系：平行于地面的惯性坐标系（x，y，z）和刚性固定在吊舱内的吊舱坐标系（x′，y′，z′）.惯性坐标系代表飞机沿直线水平飞行的坐标系，其中x轴沿飞机飞行方向，y轴在水平面上与x轴垂直，z轴与xy面垂直.当飞机正常飞行时，吊舱坐标系与惯性坐标系重合；而当吊舱姿态变化时，吊舱坐标系开始发生旋转.常见的吊舱姿态变化有三种，即摆动（roll）、倾斜（pitch）和偏航（yaw）.其中摆动是由于吊舱与飞机的连接电缆左右晃动引起的，摆动时吊舱坐标系绕x轴旋转；而吊舱的倾斜变化是由于飞机飞行速度发生变化而产生的，此时吊舱坐标系绕y轴旋转；当飞机飞行时吊舱受到侧向风的外力，会发生绕z轴旋转的偏航变化（见图2）.

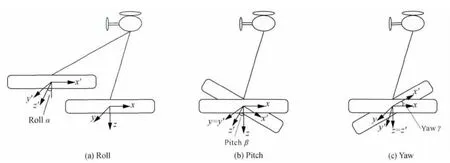
图2 常见的吊舱姿态变化示意图（a）摆动；（b）倾斜；（c）偏航.Fig.2 Sketch of common attitude changes of the bird（a）Roll；（b）Pitch；（c）Yaw.

从图2可以看出，当吊舱发生姿态变化时线圈系的方向和位置均发生了改变.线圈系的位置变化主要影响发射和接收线圈的相对位置；线圈系的方向变化主要影响磁偶极矩的大小.因此，在计算二次磁场时，需要知道姿态变化后新的收发线圈位置坐标和磁偶极矩的大小.下面分别进行推导.

2.2.1 线圈系的位置变化

由图2，发射线圈和接收线圈姿态变化后的空间位置坐标可表示为

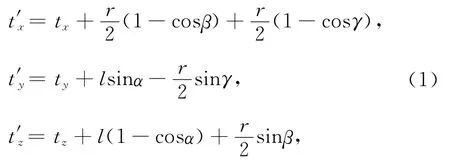
和

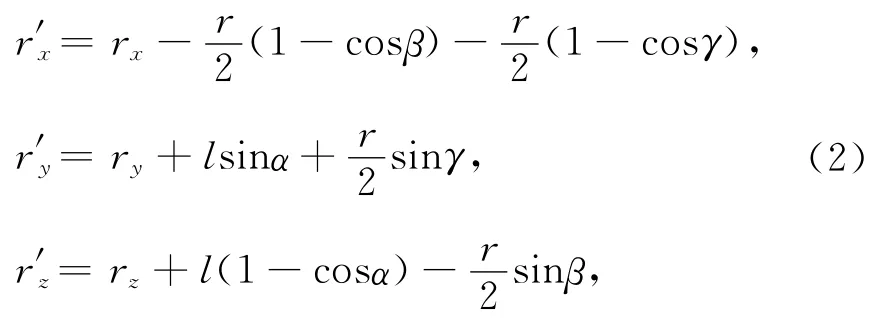
2.2.2 线圈系的方向变化

吊舱姿态变化对线圈系的方向改变主要体现在对线圈磁偶极矩的改变上.空间任意方向的磁偶极矩m均可在x，y，z三个方向上分解成分量mx、my和mz的形式

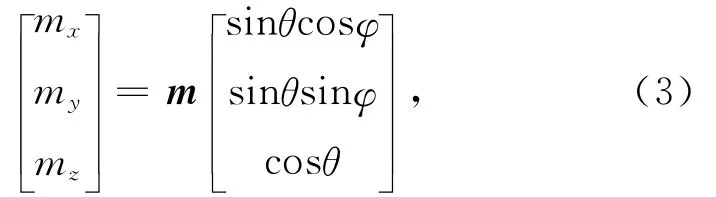
式中，θ表示磁偶极矩与z轴间的夹角，φ表示磁偶极矩在xy面上的投影与x轴的夹角.表1给出了三种线圈系姿态变化后的θ′、φ′与飞机正常飞行时的θ、φ之间的关系.

将表1中的θ′和φ′分别代入（3）中，并考虑到未发生姿态变化时HCP、VCP和VCX线圈系的（θ，φ）取值分别为（0°，0°）、（90°，90°）和（90°，0°），可得到姿态变化后磁偶极矩分量的表达式为

表1 不同线圈系不同姿态变化下的θ′、φ′角计算公式Table 1 Calculation formulas ofθ′andφ′for different coil configurations and attitude changes

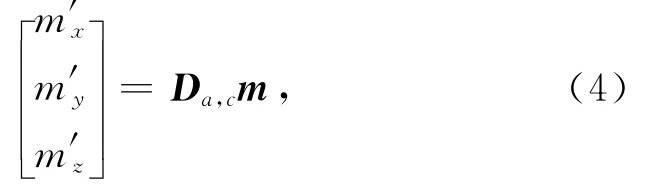
式中Da，c是旋转系数，其形式是一个3×1的矩阵.下标a表示三种姿态变化（即roll，pitch和yaw），下标c表示三种线圈系（即HCP，VCP和VCX），对于不同的线圈系，发生不同形式的姿态变化时，Da，c的取值是不同的（见表2）.

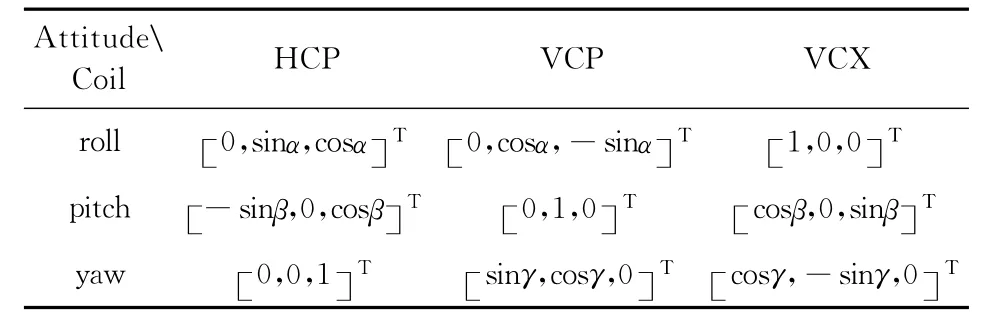
表2 不同线圈系不同姿态变化下的旋转系数Da，c的取值Table 2 Values of the rotation coefficient for different coil configurations and attitude changes

3 各向同性地层电磁响应的数值模拟

为了分析吊舱姿态变化对电磁响应的影响，本文使用频率域有限差分的数值方法模拟了吊舱姿态变化前后的二次磁场响应.为使模拟更具有一般性和代表性，需考虑水平各向同性均匀半空间的情况.

频率域散射场Maxwell方程（Chew and Weedon，1994）为

由于非磁性介质的磁导率μ与真空磁导率μ0相差无几，可取μ＝μp＝μ0＝4π×10-7H／m.在低频感应电磁法中，由于ε和εp很小（约为10-11F／m数量级），对常规地层模型（电导率为0.001～10.0S／m）来说，ωε≤σ，ωεp≤σp，故式（5）和（6）中含ε和εp的项可舍去.式（5）和（6）简化为

对式（7）两边取旋度，可得到

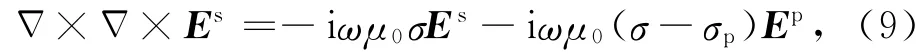
式（9）可以用交错网格有限差分法（Newman and Alumbaugh，1995）求解得到二次电场Es.由于使用磁偶极源，因此需要计算二次磁场.将二次电场Es的解代入（8）式，即可求得二次磁场值Hs.接收线圈处的电磁响应为二次磁场的电压

式中，SR为接收线圈的有效面积.未发生姿态变化时，SR等于接收线圈的面积S.当发生姿态变化时，线圈系的方向和位置均发生了改变，此时SR等于S和旋转系数Da，c的乘积，即SR＝SDa，c.因此，对于不同的线圈系（HCP、VCP和VCX），发生不同形式姿态变化（Roll、Pitch和Yaw）时的二次磁场电磁响应为

式中，ζ和η分别表示姿态变化后线圈系的方向和位置.

4 吊舱姿态变化对电磁响应的影响分析

本章共对5个模型进行了数值模拟，每个模型的地层电阻率和发射频率如表3所示.收发天线中心的距离为8m，吊舱中心点距地面距离为30m，吊舱中心到连接电缆与飞机连接点处的垂向距离为30m.对于水平各向同性均匀半空间模型，无论何种线圈系，吊舱在水平面上的旋转（即偏航）都不会对电磁响应比造成影响.因此，下文的讨论中将不再考虑偏航姿态变化.

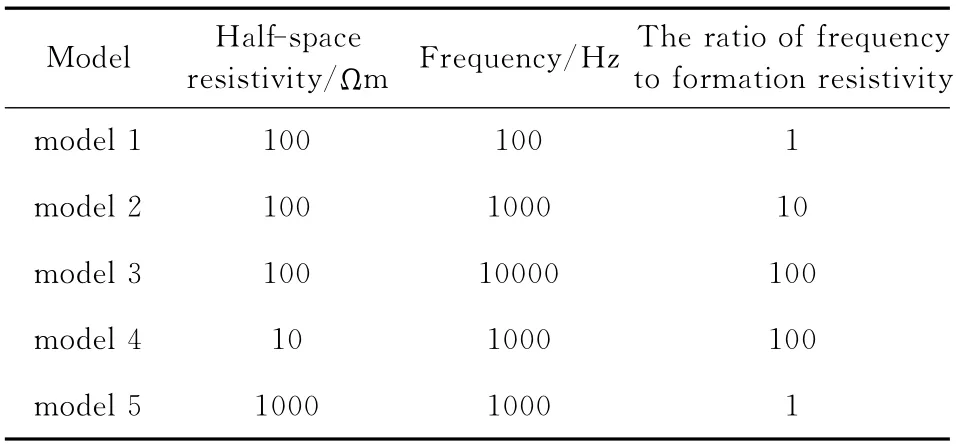
表3 五个模型的地层电阻率和发射频率值Table 3 Values of formation resistivity and transmit frequency for five different models

使用前面所推导的二次磁场计算公式以及姿态变化前后线圈系位置和磁偶极矩空间分量的表达式，可分别计算出五个模型的三种线圈系在姿态变化前后的二次磁场响应，并取两者的比值（即电磁响应比）进行分析（见图3、图4）.本文中的电磁响应比定义为

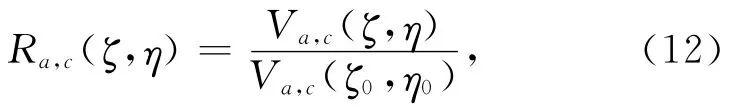
式中，ζ0和η0分别表示未发生姿态变化时的线圈系的方向和位置，ζ和η分别表示姿态变化后的线圈系的方向和位置.

4.1 摆动对电磁响应比的影响

由于在实际情况中吊舱姿态变化的角度都不大，本文的数值模拟只考虑了旋转角度小于20°的情况.图3为吊舱发生摆动后的电磁响应比.首先分析电磁响应比与模型参数的关系.从图中可以看出，无论何种线圈系何种摆动角度，都能得出以下结论：

（1）当模型的地层电阻率相同时（模型1，2，3），电磁响应比都随发射频率的升高而减小；

（2）当模型的发射频率相同时（模型2，4，5），电磁响应比都随地层电阻率的升高而增大；

（3）对于发射频率和地层电阻率的比值相同的模型（模型1和5以及模型3和4），其电磁响应比也相同，并且比值小的模型（模型1和5）的电磁响应比相对较大.

接下来考虑电磁响应比与摆动角度的关系.无论何种模型参数，HCP和VCX线圈系的电磁响应比都随摆动角度的增大而减小（图3a和3c）.而VCP线圈系电磁响应比与摆动角度的关系跟发射频率与地层电阻率的比值有关——当比值较小时（本文中为1或10），电磁响应比的变化与角度变化成正比；反之当比值较大时（本文中为100），两者的关系则成反比（图3b）.

4.2 倾斜变化对电磁响应比的影响

与摆动相似，吊舱倾斜时发射频率和地层电阻率比值相同的模型其电磁响应比也相同.而具体到每种线圈系时，倾斜则与摆动有很大不同.首先分析图4a所示的HCP线圈系.当天线发射频率与地层电阻率的比值较大时（100），电磁响应比较大；当比值较小时（1或10）电磁响应较小，并且比值为1和10的曲线很接近；而各种参数模型的电磁响应比曲线随倾斜角度的变大都是先稍微升高再明显降低.对于VCP线圈系（图4b），电磁响应比与频率电阻率比值间的关系正好与HCP的情况相反，而电磁响应比曲线随倾斜角度的变大都在降低，但是变化的幅度很小，都在1%之内.对于VCX线圈系（图4c），电磁响应比与频率电阻率比之间没有明显的关系，且电磁响应比曲线随倾斜角度的变大都在上升.

5 吊舱姿态校正

从上节的分析中可以看出，随着姿态变化角度的增大，接收线圈处的电磁响应与飞机正常飞行时的差值越来越大，这就会对后续的解释和反演造成很大的误差和多解性.所以，吊舱的姿态校正变得十分重要和势在必行.由于吊舱发生姿态变化时线圈系的方向和位置均发生了改变，可以认为是方向和位置的综合效应影响了总姿态变化的电磁响应.研究总姿态变化的校正可以从方向或位置单一变化的校正入手.

5.1 方向或位置单一变化对电磁响应比的影响

为了分析方向及位置改变对姿态变化电磁响应比的贡献，本节分别模拟了吊舱方向或位置单一变化时的情况，并分别计算了接收线圈处的电磁响应比.

图3 吊舱发生摆动时电磁响应比与摆动角度及模型参数之间的关系（a）HCP线圈系；（b）VCP线圈系；（c）VCX线圈系.Fig.3 The relation between the EM response ratio，roll angle and model parameters（a）HCP；（b）VCP；（c）VCX.

当考虑方向单一变化时，可认为收发线圈的间距为零，并且摆动和倾斜的旋转中心都为吊舱中心（实际上摆动的旋转中心为连接电缆与直升机的连接点）.图5和图6分别为吊舱发生摆动和倾斜时根据模拟结果计算出的电磁响应比.从中可以看出，当吊舱摆动时，HCP线圈系的电磁响应比与摆动角度成反比，VCP线圈系成正比，而VCX线圈系的电磁响应比则始终为1，这说明只考虑方向单一变化时，摆动对VCX线圈系无影响；而当吊舱倾斜时，HCP线圈系的电磁响应比与倾斜角度成反比，VCX线圈系成正比，而VCP线圈系的电磁响应比则始终为1，这说明只考虑方向单一变化时，倾斜对VCP线圈系无影响.

当考虑位置单一变化时，可认为在吊舱姿态变化过程中线圈系的方向始终不变，即磁偶极矩空间分量的值不变.图7和图8分别为吊舱发生摆动和倾斜时根据模拟结果计算出的电磁响应比.从中可以看出，无论吊舱是摆动还是倾斜，无论何种线圈系，电磁响应比随旋转角度的增大都是呈减小的趋势，只是HCP线圈系发生倾斜变化且角度为0°～6°时有稍许上升.不难发现图3c与图7c、图4b与图8b中的曲线形态完全一样，这说明位置单一变化对于VCX线圈系发生摆动以及VCP线圈系发生倾斜这两种情况没有影响.

5.2 校正系数的提出

图4 吊舱发生倾斜时电磁响应比与倾斜角度及模型参数之间的关系（a）HCP线圈系；（b）VCP线圈系；（c）VCX线圈系.Fig.4 The relation between the EM response ratio，pitch angle and model parameters（a）HCP；（b）VCP；（c）VCX.

图5 只考虑方向单一变化时，吊舱摆动后的电磁响应比与摆动角度及模型参数之间的关系（a）HCP线圈系；（b）VCP线圈系；（c）VCX线圈系.Fig.5 The relation between the EM response ratio，roll angle and model parameters for direction change only（a）HCP；（b）VCP；（c）VCX.

图6 只考虑方向单一变化时，吊舱倾斜后的电磁响应比与倾斜角度及模型参数之间的关系（a）HCP线圈系；（b）VCP线圈系；（c）VCX线圈系.Fig.6 The relation between the EM response ratio，pitch angle and model parameters for direction change only（a）HCP；（b）VCP；（c）VCX.

图7 只考虑位置单一变化时，吊舱摆动后的电磁响应比与摆动角度及模型参数之间的关系（a）HCP线圈系；（b）VCP线圈系；（c）VCX线圈系.Fig.7 The relation between the EM response ratio，roll angle and model parameters for position change only（a）HCP；（b）VCP；（c）VCX.

图8 只考虑位置单一变化时，吊舱倾斜后的电磁响应比与倾斜角度及模型参数之间的关系（a）HCP线圈系；（b）VCP线圈系；（c）VCX线圈系.Fig.8 The relation between the EM response ratio，pitch angle together and model parameters for position change only（a）HCP；（b）VCP；（c）VCX.

综合分析图3—图8，发现总姿态变化中电磁响应比的浮动趋势与方向和位置单一变化时电磁响应比乘积的浮动趋势相似，并且两者成一定比例.为了研究总姿态变化与方向或位置单一变化之间存在何种关系，本文计算了总姿态变化电磁响应比与方向和位置单一变化电磁响应比乘积·之间的比值（可称为校正系数）.这里表示方向和位置单一变化的电磁响应比.计算结果如图9和图10所示.

分析图9和图10，发现了一个有趣的现象——对于发生摆动的HCP和VCP线圈系以及发生倾斜的HCP和VCX线圈系，虽然五个模型的参数各不相同，但是校正系数随角度的变化曲线与旋转角度的正割曲线非常接近.而对于摆动的VCX线圈系和倾斜的VCP线圈系，校正系数的值均为1.根据这个结论，可以将总姿态变化电磁响应比（即总校正因子）与方向和位置单一变化电磁响应比（即方向和位置校正因子）之间的关系表示为

式中T即为校正系数，其取值如表4所示.分别

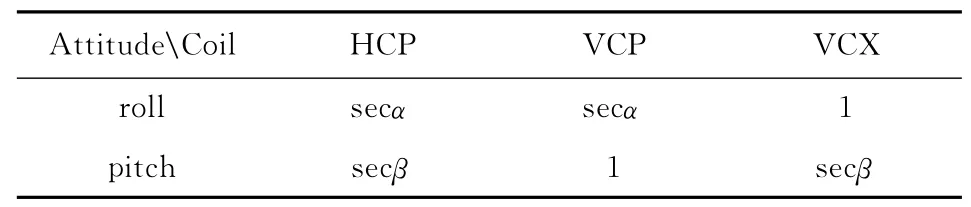
表4 不同线圈系不同姿态变化下的校正系数T的取值Table 4 Values of the correction coefficient for different coil configurations and attitude changes

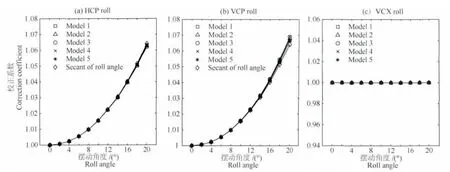
图9 吊舱摆动时的校正系数与摆动角度及模型参数之间的关系（a）HCP线圈系；（b）VCP线圈系；（c）VCX线圈系.图中菱形符表示摆动角度的正割曲线.Fig.9 The relation between the correction coefficient，roll angle，and model parameters（a）HCP；（b）VCP；（c）VCX.The diamond symbol indicates the secant function of the roll angle.

图10 吊舱倾斜时的校正系数与倾斜角度及模型参数之间的关系（a）HCP线圈系；（b）VCP线圈系；（c）VCX线圈系.图中菱形符表示倾斜角度的正割曲线.Fig.10 The relation between the correction coefficient，pitch angle and model parameters（a）HCP；（b）VCP；（c）VCX.The diamond symbol indicates the secant function of the pitch angle.

在确定了校正系数之后，下面将分别推导摆动和倾斜两种姿态变化下的方向校正因子Ra，c（ζ）和位置校正因子Ra，c（η）.

5.3 方向校正因子推导

首先考虑HCP线圈系发生摆动的情况.当α＝0°时，吊舱未发生姿态变化，电磁响应比值为1；当吊舱绕着x轴从0°旋转到90°时，HCP线圈系开始向VCP线圈系变化，由前面的分析可以得知，电磁响应比开始减小；当α＝90°时，HCP线圈系变成了VCP线圈系，经过一些实验（没有展示在这里），发现在任何水平各向同性地层均有VCP线圈系与HCP线圈系电磁响应比约为0.6，并且与地层电阻率及发射频率无关；而吊舱从90°旋转到180°时，VCP线圈系向HCP线圈系变化，电磁响应比又开始增大，直到恢复到初始值.因此，整个变化过程可以使用一个二倍角的余弦函数来表示为

相似地，可以求出HCP线圈系发生倾斜时的方向校正因子为

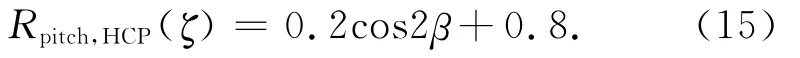
对于VCP线圈系，当其从0°摆动到90°再到180°时，其电磁响应比先增大后减小.再考虑到当α＝90°时VCP线圈系变成了HCP线圈系，其电磁响应比值变为初始值的1.67倍（0.6的倒数），可以推导出其方向校正系数为

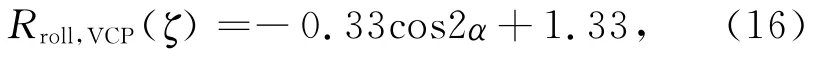
相似地，VCX线圈系发生倾斜变化时的方向校正系数为

对于水平各向同性地层模型，当只考虑线圈系的方向变化时，VCX线圈系发生摆动和VCP线圈系发生倾斜都不会改变电磁响应比值.因此，这两种情况不需要校正.综合以上分析，在表5中列出了各种情况下的方向校正因子.

表5 不同线圈系不同姿态变化下的方向校正因子计算公式Table 5 Calculation formulas of direction correction factor for different coil configurations and attitude changes

5.4 位置校正因子推导

在吊舱姿态变化角度较小时（小于20°），从前面的分析可以得知，位置单一变化会使电磁响应比减小，并且不同模型参数的电磁响应比随角度变化有些许差异.为了得到一个对于任何参数的模型都比较适用的位置校正因子，可对图7和图8中各个模型参数的曲线取平均值，得到了位置单一变化时不同线圈系不同姿态的电磁响应比平均值曲线，并用曲线拟合方法拟合出平均值曲线的表达式，这些表达式即作为本文中的位置校正因子.考虑到VCP线圈系发生倾斜变化时（图8b）的电磁响应比变化很小（小于1%），可认为该情况下的位置校正因子为1.位置校正因子的具体表达式如表6所示.

表6 不同线圈系不同姿态变化下的位置校正因子计算公式Table 6 Calculation formulas of position correction factor for different coil configurations and attitude changes

在推导出校正系数及方向和位置校正因子之后，使用式（12）即可计算出总校正因子.

6 合成数据姿态校正

本节分别使用本文提出的总校正方法和Yin的重叠偶极校正方法（Yin and Fraser，2004）对图3和图4所示的五组合成数据姿态变化后的电磁响应比进行了校正.为了评价校正结果，引入了均方根误差的定义

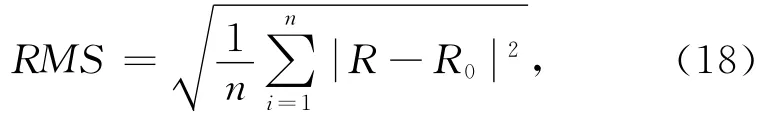
式中n为旋转角度的个数，R0和R分别为姿态变化前后的电磁响应比.本文共计算了三种均方根误差——分别是姿态变化后未校正的电磁响应比与姿态变化前电磁响应比（为1）之间的误差（用UC表示）；重叠偶极校正后的电磁响应比与姿态变化前电磁响应比的误差（用SDC表示）；总校正后的电磁响应比与姿态变化前电磁响应比的误差（用TC表示）.

图11 吊舱摆动的校正结果（a）HCP线圈系；（b）VCP线圈系；（c）VCX线圈系.图中实线表示总校正方法的校正结果，点划线表示重叠偶极校正方法的校正结果.Fig.11 Correction results of bird′s roll（a）HCP；（b）VCP；（c）VCX.The active lines indicate the corrected results using the total correction method，the chain lines indicate the corrected results using the superposed dipole correction method.

表7 吊舱摆动校正后的均方根误差Table 7 Root mean square（RMS）errors of roll correction

图11为吊舱发生摆动时的校正结果.表7为相应的均方根误差.从中可以看出，对于HCP线圈系，重叠偶极校正和总校正均能较大程度地减小电磁响应比误差；而相比较重叠偶极校正结果而言，无论何种模型参数，总校正结果曲线的值都与1更加接近，而其相应的均方根误差也较重叠偶极误差小很多.对于VCP线圈系，重叠偶极校正使得均方根误差较未校正的反而增大了很多，这是因为重叠偶极校正方法只考虑了方向校正，而没考虑位置校正；而总校正和未校正的误差很接近，并且都很小，这说明对于VCP线圈系发生摆动的情况，电磁响应比的变化并不大，可以不进行校正.对于VCX线圈系，重叠偶极校正和未校正的电磁响应比曲线以及误差都相同，这说明重叠偶极校正对VCX线圈系发生摆动的情况没有作用；而总校正的电磁响应比曲线较前两者平缓得多，均方根误差也小很多.综合以上分析可知，进行摆动校正时，总校正的结果要明显好于重叠偶极校正的结果.

图12为吊舱发生倾斜时的校正结果.表8为相应的均方根误差.从中可以看出，对于HCP和VCP线圈系，重叠偶极校正后的电磁响应比曲线以及相应的误差较之未校正的曲线和误差没有太大变化；而总校正后的电磁响应比都与1更加接近，而其相应的均方根误差也较重叠偶极误差小很多.对于VCP线圈系，两种校正方法的电磁响应比曲线以及均方根误差均与未校正的情形相同，这是因为吊舱倾斜对VCP线圈系的影响非常小，两种校正方法均不用考虑对其进行校正.综合以上分析，可以得到使用总校正方法在进行倾斜校正时能得到比重叠偶极校正方法更好校正结果的结论.

7 结论

通过对吊舱姿态变化影响的分析、校正公式的推导以及合成数据校正结果的讨论，得到以下结论：

（1）吊舱发生摆动时，电磁响应比与发射频率成反比，与地层电阻率成正比，并且发射频率与地层电阻率比值相同的模型其电磁响应比也相同，电磁响应比与该比值成反比；HCP和VCX线圈系的电磁响应比与摆动角度成反比，VCP线圈系的电磁响应比随摆动角度的变化关系与发射频率和地层电阻率的比值有关，比值小时成正比，比值大时成反比.

图12 吊舱倾斜的校正结果（a）HCP线圈系；（b）VCP线圈系；（c）VCX线圈系.图中实线表示总校正方法的校正结果，点划线表示重叠偶极校正方法的校正结果.Fig.12 Correction results of bird′s pitch（a）HCP；（b）VCP；（c）VCX.The active lines indicate the corrected results using the total correction method，the chain lines indicate the corrected results using the superposed dipole correction method.

表8 吊舱倾斜校正后的均方根误差Table 8 Root mean square（RMS）errors of pitch correction

（2）吊舱发生倾斜变化时，HCP线圈系的电磁响应比与频率和电阻率的比值成反比，VCP线圈系的情况则相反，并且两者的电磁响应比均与倾斜角度近似成反比；VCX线圈系的电磁响应比与频率和电阻率比值无确定关系，但与倾斜角度成正比.

（3）对于发生摆动的HCP和VCP线圈系以及发生倾斜的HCP和VCX线圈系，其总姿态变化的电磁响应比与方向和位置单一变化电磁响应比的乘积之比值近似等于旋转角度的正割函数；而对于发生摆动的VCX线圈系以及发生倾斜的VCP线圈系，该比值为1.

（4）总姿态变化与方向变化和位置变化有关，总校正因子可以写成方向校正因子、位置校正因子与校正系数乘积的形式.

（5）无论何种模型参数，对于任意一种线圈系和姿态变化形式，总校正均能得到比重叠偶极校正更好的校正结果.

Chew W C，Weedon W H.1994.A 3Dperfectly matched medium from modified Maxwell＇s equations with stretched coordinates.Microwave and Optical Technology Letters，7（13）：599-604.Davis A C，Macnae J，Robb T.2006.Pendulum motion in airborne HEM systems.Exploration Geophysics，37（4）：355-362.

Fitterman D V，Yin C C.2004.Effect of bird maneuver on frequency-domain helicopter EM response.Geophysics，69（5）：1203-1215.

Fitterman D V.1998.Sources of calibration errors in helicopter EM data.Exploration Geophysics，29（2）：65-70.

Fraser D C.1981.Magnetite mapping with a multicoil airborne electromagnetic system.Geophysics，46（11）：1579-1593.

Holladay J S，Lo B，Prinsenberg S J.1997.Bird orientation effects in quantitative airborne electromagnetic interpretation of pack ice thickness sounding.∥Oceans′97，Marine Technology Society Institute of Electrical and Electronic Engineers Conference Proceedings.Halifax，Canada：MTS／IEEE，2：1114-1116.

Huang H P，Fraser D C.2000.Airborne resistivity and susceptibility mapping in magnetically polarizable areas.Geophysics，65（2）：502-511.

Huang H P，Fraser D C.2002.Dielectric permittivity and resistivity mapping using high-frequency helicopter-borne electromagnetic data.Geophysics，67（3）：727-738.

Kratzer T，Vrbancich J.2006.Real-time kinematic tracking of towed AEM birds.Exploration Geophysics，38（2）：132-143.

Newman G A，Alumbaugh D L.1995.Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences.Geophysical Prospecting，43（8）：1021-1042.

Reid J E，Worby A P，Vrbancich J，etal.2003.Shipborne electromagnetic measurements of Antarctic sea-ice thickness.Geophysics，68（5）：1537-1546.

Son K H.1985.Interpretation of electromagnetic dipole-dipole frequency sounding data over a vertically stratified earth［D］.Raleigh：North Carolina State University.

Yin C C，Fraser D C.2002.The effect of the electrical anisotropy on the response of helicopter-borne frequency-domain electromagnetic systems.Geophysical Prospecting，52（5）：399-416.

Yin C C，Fraser D C.2004.Attitude corrections of helicopter EM data using a superposed dipole model.Geophysics，69（2）：431-439.

Yin C C，Hodges G.2003.Identification of electrical anisotropy from helicopter EM data.Proceedings of SAGEEP，2003：419-431.