基于非平稳相似性系数的构造导向滤波及断层检测方法

刘洋，王典，刘财＊，刘殿秘，张鹏

1吉林大学地球探测科学与技术学院，长春 130026

2中国石油吉林油田勘探开发研究院，松原 138003

1 引言

随机噪声衰减和构造保护是叠后地震数据处理中互相矛盾的两个问题.设计有效的构造导向滤波的主要难点在于达到噪声衰减和信号保护之间的平衡.直接应用叠前去噪方法进行叠后处理往往达不到理想的构造保护效果（高静怀等，2006），为此，很多叠后处理方法被用于保护和提升构造信息.一类方法主要基于局部自适应恢复模式理论，其中包括各向异性扩散（Fehmers etal.，2003）和正则化最小二乘方法（Fomel etal.，2006）.然而，这些方法依赖于迭代算法，计算效率有一些限制.近年来，更多的滤波方法被开发用以解决该问题.Hoeber etal.（2006）在平行于地震倾角的平面上应用非线性滤波方法，如，中值滤波，截断均值滤波和自适应高斯滤波，该方法建立在小的局部平面波假设基础上.AlBinHassan etal.（2006）介绍了一种有效的三维边缘保护平滑方法.Al-Dossary etal.（2007）给出了能够同时平滑地震数据和保护线性特征的滤波方法的综述.Traonmilin etal.（2008）使用有限脉冲响应（FIR）滤波器和无限脉冲响应（IIR）滤波器相结合的方法，并通过f-x滤波来实现构造保护滤波处理.Lu etal.（2009）提出了边缘保护多项式拟合方法，用以消除随机噪声干扰和保护边缘特征.Liu etal.（2010）提出将构造预测与相似性均值滤波器以及低-高-中滤波器（Lower-upper-middle，LUM）相结合的方法进行构造保护滤波.Yu etal.（2010）结合二维复数小波变换开发了角度自适应和构造一致性的滤波方法.

中值滤波是非线性信号处理中有效消除随机噪声的方法，其在地震数据处理中也得到了应用（刘财等，2007）.然而，传统的平稳中值滤波由于使用固定时窗参数，使得有效信号和噪声处于相同的处理尺度，不合适的滤波窗口选择往往导致有效信号的损失或噪声的保留.解决这个问题的一种方案是根据数据点的位置改变滤波窗口长度，例如，Liu Y etal.（2009）开发了一种自适应时变中值滤波方法.另外一种方案是使用加权中值滤波（Brownrigg，1984；Arce，1998），加权中值滤波能够提供广泛的自适应特性.尽管很多学者开发了各种权函数，但是很少有专门针对地震数据设计的.刘洋等（2011）通过设计局部相关系数改进加权中值滤波器的特性，达到保护断层信息的效果，使用地震数据的局部倾角属性设计预测构造数据体和构造走向，进而构建两种滤波策略.由于该方法仍然依赖固定数据窗口的选取，因此只适用于地震同相轴平稳性较好的区域，对于具有不同形态断层等特殊构造和非平稳同相轴的地震数据处理，存在一定的限制.

地震断面和边缘的自动检测和追踪是一项重要的工作，断层位置的识别对于理解成藏系统至关重要.很多方法被开发用于检测断层信息.廖新华等（1990）提出基于谱分解的断层自动识别方法.AlBinHassan etal.（2003）应用霍夫变换检测地震剖面和时间切片上的断层信息.de Rooij etal.（2003）应用相似性、曲率和倾角差异等多种属性综合分析断层位置.Machado etal.（2006）提出了一种断层垂直能量（Fault-vertical-energy，FVE）属性，并且结合神经网络方法来识别断层.Donias etal.（2007）提出了基于方向性特征的断层属性.Ivanova etal.（2010）提出了基于地震相关分析的自动断层检测技术.杨培杰等（2010）提出了一种方向性边界保持断层增强技术.Kamalpoor etal.（2011）使用振幅梯度中的脉冲来高亮断层位置.然而，大多数流行的断层检测技术主要依赖于相干体属性（Marfurt etal.，1998；Marfurt etal.，1999；Chopra etal.，2005）.传统的基于滑动窗口的相干体属性一般难以处理数据信息中的局部非平稳特征.

在本次研究中，通过结合构造预测和非平稳相似性属性，设计一种针对地震数据特点的权系数，完善一种加权中值滤波方法，同时基于构造预测和非平稳相似性属性，提出一种三维自动断层检测方法.

2 理论基础

提取构造信息是构造导向滤波的重要前提.Fomel（2010）提出了一种基于地震局部倾角的构造预测方法，倾角信息主要通过平面波分解滤波器（Plane-wave-destruction，PWD）刻画地震数据的局部平面波模型来求取（如附录A）.通过这种算法，可以递归地从相邻地震道预测当前地震道，预测算子按照局部倾角模式提供原始地震道的平滑估计.此时，不同预测步长条件下的预测数据即可形成一个数据体，也就意味着给原始地震数据扩展了一个数据维数——预测步长（Liu etal.，2010），预测数据体将作为构造导向滤波和断层检测的输入.构造预测的基本流程如图1所示.

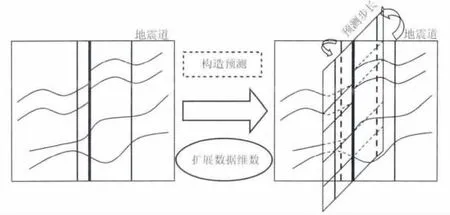
图1 构造预测流程Fig.1 Schematic illustration of structure prediction

2.1 非平稳相似性

地质层位和地震数据总是展示各种局部变化，数据驱动模式和非平稳的基本特征可以针对地震数据进行设计.相似性是衡量两个信号差异的一种属性.两个不同的信号a（t）和b（t）的全局相关系数可以表示为

在线性代数表达形式下，相关系数γ的平方可以表示为两个最小二乘反演的乘积（Fomel，2007a）：

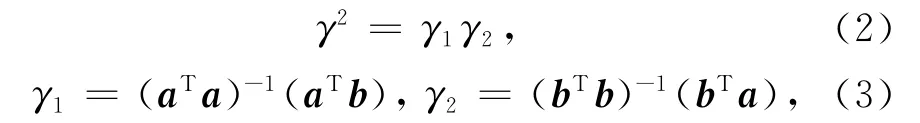
其中，a为a（t）的矢量形式，b为b（t）的矢量形式，xTy表示公式（1）中的积分运算.如果用a和b数据组成矩阵A和B的对角线元素，则对公式（3）进行局部平滑等于对该反演加入正则化，此时标量γ1和γ2对应的矢量c1和c2可以通过整形正则化定义为（Fomel，2007b）

其中，I代表单位算子，λ为调整A和B幅值的比例系数，S是整形正则化算子.最终，矢量c1和c2的对应分量乘积定义为非平稳相似性系数.整形正则化的优势在于，正则化算子的平滑半径参数选取为固定值，仍然能够保证数据空间的平滑性根据数据位置的不同进行局部自适应调整，因此表征非平稳信号的局部特性，同时还保证调节参数的最少化.该属性为构造导向滤波和断层检测提供新的属性，这个属性同样可以用于地震数据加权叠加（Liu G C etal.，2009）.

2.2 基于非平稳相似性系数的加权中值滤波

在统计估计理论中，独立同分布（i.i.d）条件下样本序列（x1，x2，…，xN）的中值服从拉普拉斯分布，是样本的最大概似（ML）估计.广义的中值概念可以通过扩展最大概似估计理论得到.假设样本序列只服从相同的概率分布，但是每个样本的方差不具有相同的分布，则序列的最大概似估计值x＾使得加权绝对偏差的和

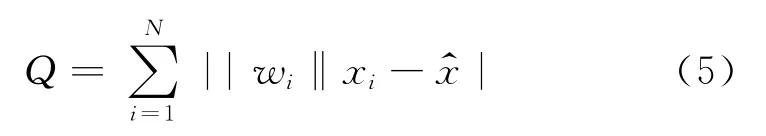
达到最小.其中，wi为权系数.

公式（5）中的x＾即为Edgemorth（1888）引入的加权中值，并被定义为

由于非平稳相似性系数的数值为非整数，因此引入非整数加权中值滤波的计算步骤：

（2）将“带有权系数符号”的数据序列sign（wi）xi按照从大到小的顺序排列，同时交换数据所对应权系数的位置，排成新的权系数序列（此处权系数值无特殊排序）；

（3）将新排序的权系数依次累加；

（4）当加上某一个权系数且累加数等于或大于T时，则输出对应数据作为加权中值结果.

为了实现构造导向加权中值滤波方法，首先将预测数据沿预测步长方向进行叠加，叠加结果作为平滑的参考数据，然后加权中值滤波的权系数等于在不同预测步长下预测数据（包含原始数据）与参考数据之间的非平稳相似性系数.根据公式（2），由相似性系数得到的权系数符号均为正.此时，依赖于时间方向平滑的权系数不再属于统计范畴，而产生了数据驱动特征.最后，在预测数据体中选择相对原始数据相似性最大的平滑估计作为构造导向滤波的输出结果.

2.3 基于非平稳相似性系数的断层检测方法

基于滑动窗口的局部相干方法可以检测两个信号相似性，这种方法是平稳的，即一旦选择好窗口长度，对于任意一点数据的测量都按照同一个尺度进行.非平稳相似性属性通过正则化条件将局部平滑隐含在数学反演中，相当于在每个数据点的位置选取不同大小的平滑窗口，而保证隐含的相同平滑性，是一种非平稳的方法.断层信息一般在时空方向是不可预测的，因此，在构造数据体中预测数据与原始数据之间小数值的相似性系数可以用于指示断层的位置.较远的预测距离往往失去构造预测的准确性，因此在二维数据断层检测中，选取原始地震道的左侧和右侧相邻各1道进行构造预测.两个预测切片形成预测数据体，这个过程消除了地震数据中由于地层的弯曲所引起的小相似性数值.三维构造预测方法可以通过Fomel的方法得到（Fomel，2010）.叠加一个预测步长下计算的非平稳相似性系数（二维为左右相邻各1道，三维为所有相邻的8道）能够指示断层的位置，对叠加系数的平方运算能够进一步高亮断层的位置.本文断层检测的主要步骤如下：

（1）对高信噪比地震数据（如构造导向滤波结果）求取地震局部倾角；

（2）基于局部倾角形成不包括原始数据的预测数据体（此处区别于构造导向滤波）；

（3）计算原始地震数据与预测数据之间的非平稳相似性系数；

（4）沿着预测步长方向叠加非平稳相似性系数，并且计算叠加值的平方.

基于非平稳相似性系数的构造导向滤波和断层检测方法的具体流程将以二维实际数据为例进一步说明.

3 理论模型

为了验证本文方法，选取三维“qdome”模型（Claerbout，2012）进行测试（图2a），该模型包含顶部的水平地层、中部的高斯型地层、底部的倾斜地层、不同类地层区域边界的水平不整合面以及一个倒穹窿状的断层.图中三个侧面分别代表三维数据体内部标识线位置的切片（前侧面为联络测线0.45km位置的主测线剖面，右侧面为主测线1.25km位置的联络测线剖面，顶侧面为时间0.82s的时间切片）.图2b为加入正态分布随机噪声以后的三维地震记录.由于三维数据的构造预测结果为四维数据，因此此处只显示处理结果，具体的处理流程在后面的二维实际数据处理中给出.应用本文提出的构造导向加权中值滤波结果如图2c所示，此处选取每个参考道周围2个预测步长距离的地震道（共24道）进行构造预测，计算相似性系数时选取整形正则化算子的平滑半径等于10个时间采样点.从处理结果可以看到，随机噪声得到有效地衰减，主要断层的位置得到保留.图2d为图2b和图2c的差异剖面，该剖面主要为消除的随机噪声，连续的地层信息未出现在差异剖面中，证明构造预测能够有效地预测连续地层的走向，同时差异剖面中可以看到一些弱的断层信息，这是由于断点位置的波场往往表现与随机噪声相似的特点，因此一些弱的断点信息被部分地衰减，但在去噪后的结果（图2c）中，仍然可以清晰地判断大多数的断层位置.

接下来测试本文的断层检测方法，首先以构造导向滤波结果（图2c）作为输入数据，同时计算主测线和联络测线两个方向的同相轴倾角，并且选取1个预测步长距离的8个相邻地震道进行构造预测，为了保证断层的分辨率，此处的整形正则化算子的平滑半径减小到5个时间采样点，最终得到的断层位置如图3a所示，从图中可以看到，非平稳穹隆状断层所表现出的曲线特征和不同断距特点被清晰地指示出来，然而结果中仍然有一些连续地层的弱能量阴影.为了分析这个结果，进一步将理论无噪声数据（图2a）作为检测对象，通过选取相同的参数，断层检测结果（图3b）比较理想地显示出断层的位置.对比结果说明了剩余噪声对于本文断层检测方法有一定的影响，尽管如此，图3a的结果仍然验证了本次研究提出的构造导向滤波和断层检测方法具有较好的工业可应用性.

图2 三维qdome模型构造导向滤波测试结果（a）三维合成地震记录；（b）加入随机噪声的模型数据；（c）构造导向加权中值滤波结果；（d）差异剖面.Fig.2 Tests of structure-oriented filtering for 3Dqdome model（a）3Dsynthetic data；（b）Seismic data after adding random noise；（c）Result after structure-oriented weighted median filtering；（d）Difference section.

图3 理论模型断层检测结果（a）图2c的断层检测结果；（b）图2a的断层检测结果.Fig.3 Results of fault detection for synthetic model（a）Fault detection for Fig.2c；（b）Fault detection for Fig.2a.

4 实际数据

选取墨西哥湾某地区的二维时间偏移剖面对本文方法进行测试（Claerbout，2008）（图4a）.首先，应用平面波分解滤波器进行局部倾角估计，如图4b所示.估计的倾角能够准确地描述数据中的地层倾向.接下来，根据局部倾角模式选取相邻道对每一道地震数据进行预测，此处选取共14个预测步长（左右各7道），连同原始数据共同组成了预测数据体（图4c），新增的预测步长数据坐标来自公式（A4）.沿着预测步长方向数据信息呈现水平趋势，可以验证平面波分解滤波器很好地预测局部构造走向.同时，可以看到数据体中有一些由断层产生的中断位置，沿预测步长方向叠加预测数据体得到光滑的参考数据，选取时间方向平滑半径为10的整形正则化算子，计算预测数据与参考数据之间的非平稳相似性系数，如图4d.为了比较，选取相似性加权均值方法（Liu etal，2010）对预测数据体（图4c）进行处理，如图5a所示，相似性加权均值方法能够提高构造的连续性，但是对断点的位置有一些模糊效应.另一种选择是使用本文的加权中值滤波方法进行处理，应用图4d中的相似性值作为权系数沿着预测步长方向在预测数据体中选取加权中值，去噪的结果如图5b所示，此时断层的边缘更加清晰，同时信噪比得到提高.

进一步计算原始剖面（图4a）和构造导向滤波结果（图5a、5b）之间的差异剖面.为了便于比较，使用了相同的增益值和绘图参数，从图5c和5d可以看到，两种方法很好地保护了连续同相轴，证明了构造预测可以很准确地预测相干信息.相似性均值滤波结果显示一些边界效应，而加权中值滤波能够有效地避免边界效应，同时消除了更多断层附近的散射波，使得断层的边缘更加清晰.

图4 实际二维数据构造预测及权系数估计（a）实际地震数据；（b）地震局部倾角；（c）预测数据体；（d）非平稳相似性系数.Fig.4 Structure prediction and weight coefficients estimation for 2Dfield data（a）Field data；（b）Local slopes；（c）Prediction datacube；（d）Nonstationary similarity.

图5 构造导向滤波结果对比（a）构造导向加权均值滤波结果；（b）构造导向加权中值滤波结果；（c）图4a和图5a的差剖面；（d）图4a和图5b的差剖面.Fig.5 Results after structure-oriented filtering（a）Result after structure-oriented weighted mean filtering；（b）Result after structure-oriented weighted median filtering；（c）Difference section between Fig.4aand Fig.5a；（d）Difference section between Fig.4aand Fig.5b.

对于断层检测，需要高信噪比的叠后地震数据，构造导向加权中值滤波提供了所需要的输入数据（图5b）.首先应用平面波分解滤波器重新估计去噪后地震数据的倾角，如图6a所示.此时，根据局部倾角模式用邻道对原始道进行预测.选取2个预测步长（左右各1道）生成新的预测数据体（图6b）.地震同相轴沿着预测方向呈现水平的趋势，同时断层的存在产生了一些同相轴的中断.两个预测数据切片与图5b进行比较，计算出非平稳相似性系数，如图6c所示，该系数衡量原始数据与其预测数据之间的局部相干性.进一步对相似性系数沿预测方向叠加并求取算数平方得到最终的断层信息，结果很清晰地指示出断层的位置（图6d）.为了进一步比较，选取标准的C1相干算法对图5b中的断层位置进行计算，结果如图6e所示.图6d和图6e使用相同的色标进行显示，但C1相干算法无法消除同相轴对断层检测的影响，另外，检测的断层也较模糊.

接下来测试三维情况，选取墨西哥湾某地区的三维叠后数据体进行处理（Liu etal，2010），该数据体带有一个倒圆锥形状的断层，如图7a所示.为了避免损失三维数据每个空间方向的信息，选取共24个预测地震道（每个当前道周围2个预测步长距离的地震道），连同原始地震数据，可以生成一个四维数据体，此时平面波分解滤波器同时计算主测线和联络测线方向的同相轴倾角.非平稳相似性衡量预测数据体之间的差异，这个属性被进一步用于构建加权中值滤波的权系数.图7b显示了构造导向滤波后的结果，既有效地消除了随机噪声又很好地保护了断层信息.图7c显示了原始数据（图7a）和基于加权中值的构造导向滤波后数据（图7b）的差异剖面，与二维数据处理结果相似，构造导向加权中值滤波能够很好地保护相干性信号，没有明显的有用信息出现在差异剖面中.该叠后地震数据信息相对丰富，直接判断剖面中的断层位置比较困难，因此，将去噪后的结果作为本文断层检测方法的输入进行计算.选取8个预测道（每个地震道周围1个预测步长距离的相邻道）能够再次得到一个四维预测数据体.非平稳相似性系数显示了原始数据与其预测数据的差异，沿着预测步长方向对相似性系数进行叠加并且求取平方的结果指示了断层的位置，如图7d所示.

图6 二维实际数据断层检测结果（a）地震局部倾角；（b）预测数据体；（c）非平稳相似性系数；（d）本文方法计算断层位置；（e）C1相干方法计算断层位置.Fig.6 Results of fault detection for 2Dfield data（a）Local slopes；（b）Prediction datacube；（c）Nonstationary similarity；（d）Fault position calculated by proposed method；（e）Fault position calculated by C1coherency method.

5 结论

本文改进了新的构造导向滤波方法并提出了新的断层检测方法，这两种方法由非平稳相似性属性和构造预测构成，但是选择的参数不同.根据地震同相轴的局部构造走向，本文使用构造预测方法通过相邻道对原始道进行预测，在预测数据体中计算非平稳相似性系数来定义加权中值滤波的权系数，这种非线性方法从预测数据体中选取最佳的数据输出作为去噪结果.基于不同参数的构造预测，计算得到的非平稳相似性系数同时能够指示断层位置.本文提出构造导向滤波方法的精度取决于地震局部倾角的预测，PWD方法能够较准确地获取低信噪数据中的局部倾角，但对于信噪比非常低的情况，建议应用其他方法，如f-x预测滤波（Liu etal.，2012），等.基于非平稳相似性系数的断层检测方法相对于常规相干体算法具有更好的效果，但是本方法基于构造预测，所以在占用内存和计算效率方面要低于相干体方法，然而叠后数据量一般较小，因此本方法仍可以在实际处理中应用.通过理论模型和实际数据的处理结果分析，这两种方法的匹配能够有效消除随机噪声同时很好地保护地震信号的细节，有效地指示断层的位置.最后，本文提出的两种技术可以分别与其他构造平滑方法或断层检测方法进行组合，增加了方法使用的灵活性.

图7 实际三维数据测试结果（a）三维实际数据；（b）构造导向滤波结果；（c）差异剖面；（d）断层位置.Fig.7 Results of 3Dfield data processing（a）3Dfield data；（b）Result after structure-oriented filtering；（c）Difference section；（d）Fault position.

致谢 感谢美国德州大学奥斯汀分校Fomel Sergey教授的建议和帮助.感谢Texaco公司提供的墨西哥湾三维叠后地震数据.作者感谢两位匿名审稿人提出的宝贵意见.

附录A

构造预测

其中，d为残差，D为非平稳平面波分解滤波器，并且有如下定义：

其中，σi为局部倾角，Pi，j（σi）为从第i道到第j道的预测因子，I和Pi，j为M×1维的矩阵.地震道的预测过程是原始地震道沿主地震倾角方向的时移运算.地震局部倾角~σ可以由对预测误差d这一目标函数求极小值来估计（Fomel，2002）

其中，ε是正则化比例系数，S是整形正则化算子（Fomel，2007），该正则化算子控制局部倾角的平滑性，该算子也可以用Tikhonov正则化（Tikhonov，1963）算子代替.通过公式（A3）得到的局部倾角可以进一步计算预测因子Pi，j，对于相距较远的地震道之间预测可以由递归来实现，例如，从第1道到第k道的预测为：

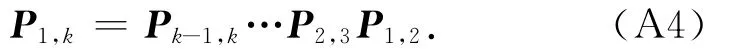
AlBinHassan N M，Luo Y，Al-Faraj M N.2006.3Dedgepreserving smoothing and applications.Geophysics，71（4）：P5-P11.

AlBinHassan N M，Marfurt K J.2003.Fault detection using Hough transforms.73rd Ann.Internat Mtg.，Soc.Expi.Geophys.Expanded Abstracts，1719-1721.

Al-Dossary S，Marfurt K J.2007.Lineament-preserving filtering.Geophysics，72（1）：P1-P8.

Arce G R.1998.A general weighted median filter structure admitting negative weights.IEEE Transaction on Signal Processing，46（12）：3195-3205.

Brownrigg D R K.1984.The weighted median filter.Communications of the ACM，27（8）：807-818.

Chopra S，Marfurt K J.2005.Seismic attributes—A historical perspective.Geophysics，70（5）：3SO-28SO.

Claerbout J F，Fomel S.2012.Image estimation by example：Geophysical soundings image construction.Stanford Exploration Project，http：∥sepwww.stanford.edu／sep／prof／.

Claerbout J F.2008.Basic Earth imaging.Stanford Exploration Project，http：∥sepwww.stanford.edu／sep／prof／.

de Rooij M，Tingdahl K.2003.Fault detection with meta-attributes.73rd Ann.Internat Mtg.，Soc.Expi.Geophys.Expanded Abstracts，354-357.

Donias M，David C，Berthoumieu Y，etal.2007.New fault attribute based on robust directional scheme.Geophysics，72（4）：P39-P46.

Edgeworth F Y.1888.On a new method of reducing observations relating to several quantities.Philosophical Magazine Series 5，25（154）：184-191.

Fehmers G C，Hôcker C F W.2003.Fast structural interpretation with structure-oriented filtering.Geophysics，68（4）：1286-1293.

Fomel S，Guitton A.2006.Regularizing seismic inverse problems by model reparameterization using plane-wave construction.Geophysics，71（5）：A43-A47.

Fomel S.2002.Applications of plane-wave destruction filters.Geophysics，67（6）：1946-1960.

Fomel S.2007a.Local Seismic Attributes.Geophysics，72（3）：A29-A33.

Fomel S.2007b.Shaping regularization in geophysical-estimation problems.Geophysics，72（2）：R29-R36.

Fomel S.2010.Predictive painting of 3Dseismic volumes.Geophysics，75（4）：A25-A30.

Gao J H，Mao J，Man W S，etal.2006.On the denoising method of prestack seismic data in wavelet domain.Chinese J.Geophys.（in Chinese），49（4）：1155-1163.

Hoeber H，Brandwood S，Whitcombe D.2006.Structurally consistent filtering.68th Annual International Conference and Exhibition，EAGE.Expanded Abstracts.

Ivanova N L，Averbukh A G，Ahmetova E R.2010.Automatic fault detection based on seismic data correlation analysis.72nd Annual International Conference and Exhibition，EAGE.Expanded Abstracts.

Kamalpoor M，Siahkoohi H R.2011.Fault detection using spikes in complex seismic trace attribute.73rd Annual International Conference and Exhibition，EAGE.Expanded Abstracts.

Liao X H，Yan P F，Chang T.1990.Automatic faults recognition using spetrum decomposition.Chinese J.Geophys.（in Chinese），33（2）：220-226.

Liu C，Li H X，Tao C H，etal.2007.A new fuzzy nesting multilevel median filter and its application to seismic data processing.Chinese J.Geophys.（in Chinese），50（5）：1534-1542.

Liu G C，Chen X H，Du J，Wu K L.2012.Random noise attenuation using f-xregularized nonstationary autoregression.Geophysics，77（2）：V61-V69.

Liu G C，Fomel S，Jin L，etal.2009.Stacking seismic data using local correlation.Geophysics，74（3）：V43-V48.

Liu Y，Fomel S，Liu G C.2010.Nonlinear structure-enhancing filtering using plane-wave prediction.Geophysical Prospecting，58（3）：415-427.

Liu Y，Liu C，Wang D.2009.A 1Dtime-varying median filter for seismic random，spike-like noise elimination.Geophysics，74（1）：V17-V24.

Liu Y，Wang D，Liu C，etal.2011.Weighted median filter based on local correlation and its application to poststack random noise attenuation.Chinese J.Geophys.（in Chinese），54（2）：358-367.

Lu Y H，Lu W K.2009.Edge-preserving polynomial fitting method to suppress random seismic noise.Geophysics，74（4）：V69-V73.

Machado M，Vellasco M，Silva P M，etal.2006.Providing spatial coherence information to fault meta-attribute.76th Ann.Internat Mtg.，Soc.Expi.Geophys.Expanded Abstracts，1113-1117.

Marfurt K J，Kirlin R L，Farmer S L，etal.1998.3-D seismic attributes using a semblance-based coherency algorithm.Geophysics，63（4）：1150-1165.

Marfurt K J，Sudhaker V，Gersztenkorn A，etal.1999.Coherency calculations in the presence of structural dip.Geophysics，64（1）：104-111.

Tikhonov A N.1963.Solution of incorrectly formulated problems and the regularization method.Soviet Mathematics-Doklady.

Traonmilin Y，Herrmann P.2008.Structurally consistent f-x filtering.78th Ann.Internat Mtg.，Soc.Expi.Geophys.Expanded Abstracts，2642-2646.

Yang P J，Mu X，Zhang J T.2010.Orientational edge preserving fault enhance.Chinese J.Geophys.（in Chinese），53（12）：2992-2997.

Yu Z，Whitcombe D N，Hodgson L.2010.Dip-adaptive structurally conformable filtering using a 2Dcomplex wavelet transform.80th Ann.Internat Mtg.，Soc.Expi.Geophys.Expanded Abstracts，3534-3538.

附中文参考文献

高静怀，毛剑，满蔚仕等.2006.叠前地震资料噪声衰减的小波域方法研究.地球物理学报，49（4）：1155-1163.

廖新华，阎平凡，常迵.1990.基于谱分解的断层自动识别.地球物理学报，33（2）：220-226.

刘财，李红星，陶春辉等.2007.模糊嵌套多级中值滤波方法及其在地震数据处理中的应用.地球物理学报，50（5）：1534-1542.

刘洋，王典，刘财等.2011.局部相关加权中值滤波技术及其在叠后随机噪声衰减中的应用.地球物理学报，54（2）：358-367.

杨培杰，穆星，张景涛.2010.方向性边界保持断层增强技术.地球物理学报，53（12）：2992-2997.