几种常见BCD码在同步时序逻辑电路中的对比分析
严李强,郭玉萍,刘重显
(西藏大学 工学院,西藏 拉萨 850000)
几种常见BCD码在同步时序逻辑电路中的对比分析
严李强,郭玉萍,刘重显
(西藏大学 工学院,西藏 拉萨 850000)
BCD码也称二进码十进数。根据实际需求,BCD码产生了多种编码形式。选择不同的BCD码来完成电路设计,则逻辑电路会呈现出不同的结构和工作过程。本文选择同步时序逻辑电路设计中的一个具体实例,采用常见BCD码的六种形式分别完成一次完整设计,对比分析各种编码形式对逻辑电路设计的可靠性、自启动能力、电路结构和元器件利用率的影响。
BCD码;同步时序逻辑电路;有权码;无权码
在逻辑电路设计时常常选择容易理解的自然二进制码作为编码分配方案,由于这种码字存在的缺陷,容易导致逻辑电路出现竞争冒险。是否在逻辑电路设计中存在一种码字,使得逻辑电路的可靠性、自启动能力、电路结构和元器件的利用率等问题都得到最优解?在十进制与二进制的换算中除了自然二进制码以外,还有二十进制码(BCD码)。它是在自然二进制的基础进一步衍化出的编码形式,它又包括多种编码形式,每一种编码形式都有各自的特点,这在设计逻辑电路时又会引起不同的表现。
1 常见 BCD码
BCD码可分为有权码和无权码两类。其中,常见的有权BCD码有8421码、2421码、5421码,无权BCD码有余3码、余3循环码、格雷码。6种常见码字的关系对照表如表1所示。
8421 BCD码是最基本和最常用的BCD码,它和四位自然二进制码相似,各位的权值为8、4、2、1,故称为有权BCD码。5421BCD码和2421BCD码同为有权码,它们从高位到低位的权值分别为5、4、2、1和2、4、2、1。
余3码是由8421码加3后形成的,是一种“对9的自补码”。余3循环码是一种变权码,每一位的在不同代码中并不代表固定的数值,主要特点是相邻的两个代码之间仅有一位的状态不同。格雷码(也称循环码)是由贝尔实验室的Frank Gray在1940年提出的,用于PCM方法传送信号时防止出错。格雷码是一个数列集合,它是无权码,它的两个相邻代码之间仅有一位取值不同。余3循环码是取4位格雷码中的十个代码组成的,它同样具相邻性的特点。

表1 几种常见的BCD码Tab.1 Several common BCD codes
2 同步时序逻辑电路的设计步骤
设计同步时序逻辑电路的一般步骤[1]如下。
1)由给定的逻辑功能建立原始状态图和原始状态表。
2)状态化简。在保证满足逻辑功能要求的前提下,将等价状态(如果两个状态作为现态,其任何相同输入所产生的输出及建立的次态均完全相同,则这两个状态称为等价状态)合并为一个状态。
3)状态分配,即对每个状态指定一个特定的二进制代码,称为状态分配或状态编码[2-3]。状态分配的任务就是在保证电路稳定工作的前提下寻求一种可靠性较好,电路结构最简单,且能自启动的最佳状态分配方案。不同的状态分配方案会导致不同的逻辑电路结构,结构简单的逻辑电路通常所需的芯片或门电路就越少,运行时间就越短,工作效率会相对较高,成本价格就越低。
通常采用自然二进制数进行编码。M为电路的状态数。每个触发器表示一位二进制数,因此,触发器的数目n可按下式确定:

4)选择触发器。一般可选JK触发器或D触发器。
5)确定激励方程组和输出方程组,求出状态方程组。
6)画出逻辑图,并检查电路有无自启动能力。
3 设计举例
为了有效对比常见的BCD码在同步时序逻辑电路中的差异,选择“设计同步十进制加法计数器”为例;同时,选择使用D触发器来完成设计,以期望得到最简单的电路结构[4-5]。
3.1 使用2421码设计
1)列出原始状态图,如图1所示。

图1 原始状态图Fig. 1 Original state diagram
2)状态化简。使用2421码状态分配方案时状态是一一对应的,不需要化简。
3)状态编码。使用2421码进行状态编码,如表1所示。4)选择触发器,并确定激励方程组和状态方程组。
根据式(1)计算得触发器个数n=4,即需要4个D触发器构成。由上述步骤可得十进制加计数器的真值表,如表2所示。
由上述真值表画出电路输出信号的卡诺图,如图2所示。
由卡诺图化简得到激励与状态方程组如下:


表2 2421码同步十进制加计数器的状态表Tab.2 State table of 2421 code synchronous decimal counter

图2 2421码同步十进制加计数器的卡诺图Fig. 2 Karnaugh map of 2421 code synchronous decimal counter
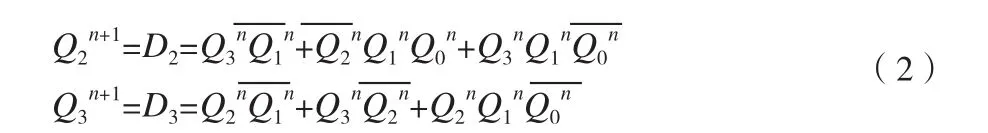
5)根据得出的方程组画出逻辑电路图,如图3所示。
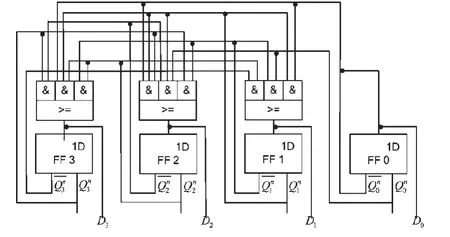
图3 2421码同步十进制加计数器的逻辑电路图Fig. 3 Logic circuit diagram of 2421 code synchronous decimal counter
6)检查自启动能力。其中6个冗余态(0101、0110、0111、1000、1001、1010)经过状态方程组运算,在一、两个时钟周期后全部都能进入有效循环状态,电路具有自启动能力。画出完全状态图,如图4所示。
3.2 使用5421码设计
同理,使用5421码完成设计过程产生的逻辑电路图和完全状态图如图5和图6所示。
3.3 使用8421码设计
同理,使用8421码完成设计过程产生的逻辑电路图和完全状态图如图7和图8所示。
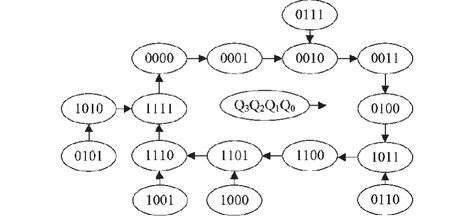
图4 2421码同步十进制加计数器的完全状态图Fig. 4 Completely state diagram of 2421 code synchronous decimal counter
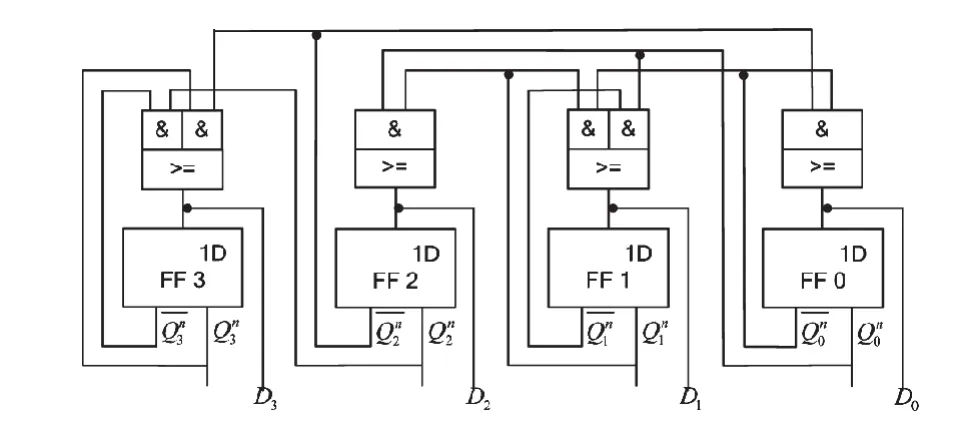
图5 5421码同步十进制加计数器的逻辑电路图Fig. 5 Logic circuit diagram of 5421 code synchronous decimal counter

图6 5421码同步十进制加计数器的完全状态图Fig. 6 Completely state diagram of 5421 code synchronous decimal counter

图7 8421码同步十进制加计数器的逻辑电路图Fig. 7 Logic circuit diagram of 8421 code synchronous decimal counter

图8 8421码同步十进制加计数器的完全状态图Fig. 8 Completely state diagram of 8421 code synchronous decimal counter
3.4 使用余3码设计
同理,使用余3码完成设计过程产生的逻辑电路图和完全状态图如图9和图10所示。

图9 余3码同步十进制加计数器的逻辑电路图Fig. 9 Logic circuit diagram of excess-three code synchronization decimal counter
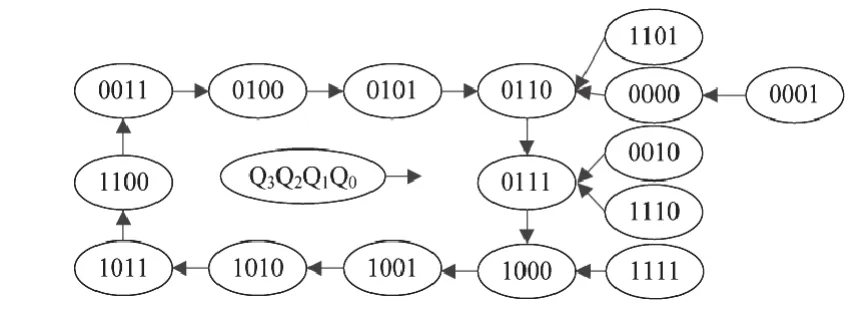
图10 余3码同步十进制加计数器的完全状态图Fig. 10 Completely state diagram of excess-three code synchronization decimal counter
3.5 使用余3循环码设计
同理,使用余3循环码完成设计过程产生的逻辑电路图和完全状态图如图11和图12所示。
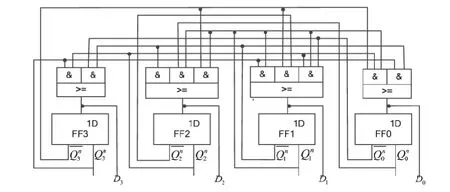
图11 余3循环码同步十进制加计数器的逻辑电路图Fig. 11 Logic circuit diagram of excess-three cyclic code synchronization decimal counter

图12 余3循环码同步十进制加计数器的完全状态图Fig. 12 Completely state diagram of excess-three cyclic code synchronization decimal counter
3.6 使用格雷码设计
同理,使用格雷码完成设计过程产生的逻辑电路图和完全状态图如图13和图14所示。
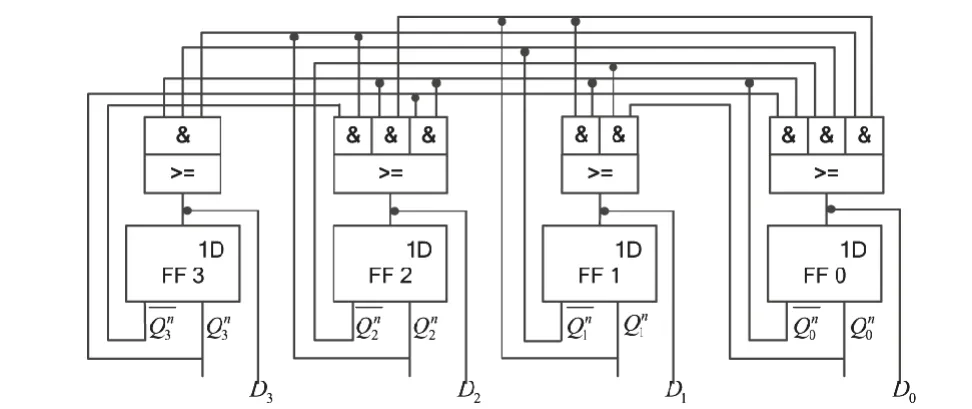
图13 格雷码同步十进制加计数器的逻辑电路图Fig. 13 Logic circuit diagram of Gray code synchronization decimal counter

图14 格雷码同步十进制加计数器的完全状态图Fig. 14 Completely state diagram of Gray code synchronization decimal counter
4 举例结果分析
4.1 概念定义
为了有效对比表1中六种BCD码在同步时序逻辑电路设计中的差别,在此定义以下4个基本概念。
1)逻辑电路的可靠性是指设计好的逻辑电路是否存在竞争冒险的问题。竞争冒险是数字电路中普遍存在的一种现象。如果一个数字电路从一个稳定状态转换到另一个稳定状态时,其中某个门电路的两个输入信号同时向相反方向变化,即某个输入信号的某一变量出现由原变非的同时也由非变原,称该电路存在竞争[1]。
2)逻辑电路的自启动能力是指冗余态是否能自动返回到电路的有效工作状态;若能,则需进一步考虑是直接返回有效状态,还是间接返回有效状态。
3)逻辑电路的结构复杂度是使用指定芯片的个数问题。当使用芯片较多时,电路运行过程所需的时间也会相应的增加,此时该电路的效率也会随之降低,则认为该电路的结构较为复杂。
4)逻辑电路的元器件利用率是芯片中逻辑门的使用情况,当芯片中没有使用的门越多时,表示该芯片的使用率越低,即元器件的利用率较低。
4.2 各码字对应逻辑电路的芯片使用情况
图3、5、7、9、11和13中统一使用74LS32(二输入四或门)芯片、74LS08(二输入四与门)芯片和74LS175(四D触发器)芯片来实现逻辑电路的实物,则各自的芯片使用情况如表3所示。

表3 芯片使用情况统计表Tab.3 Chip usage statistics单位:个
4.3 各码字对应逻辑电路的性能比较
在概念定义的基础上,分析表1中一个状态向下一个状态过渡时不同编码形式的表现,分析图3、5、7、9、11和13的电路结构,分析图4、6、8、10、12和14的自启动情况,分析表3中不同编码形式引起的芯片使用情况,可得出六种码字在可靠性、自其动能力、电路结构复杂度和元器件利用率4各方面的对比结果,如表4所示 。

表4 各码字性能比较结果Tab.4 Comparison results of each code word performance
5 结束语
由于编码方式的原因,即无权码中的余3码是由有权码中的8421码加3得到的,余3循环码是格雷码加3得到的,8421码和余3码设计所得电路的性能相差不大,余3循环码和格雷码设计所得电路也颇为类似。整体来看,6种码字中除了2421码的各方面表现差以外,其余5种码字都各有优势;因此,在逻辑电路设计时需要结合具体情况来选择二进制的编码形式方可实现最佳逻辑电路设计。
[1] 康华光.电子技术基础-数字部分[M].5版.北京:高等教育出版社,2006.
[2] 王新.同步时序电路设计的状态分配技术[J].云南民族学院学报:自然科学版,1999.8(2):1-5.
WANG Xin.State assignment's technology of synchronous sequential circnit design[J].Journal of Yunnan Institute of the Nationalities:Natural Sciences Edition,1999,8(2):1-5.
[3] 王函韵,吴训威.对冗余态的状态分配技术[J].杭州大学学报:自然科学版,1997,24(1):45-50.
WANG Han-yun,Wu Xun-wei.A state assignment technique for redundent states[J].Journal of Hangzhou University:Natural Science,1997,24(1):45-50.
[4] 任骏原.基于数据选择器和D触发器的多输入时序电路设计[J].现代电子技术,2010(12):10-12.
REN Jun-yuan.Design of data multi-input sequential logic circuit based on data multiplexer and D flip-flop[J].Modern Electronics Technique,2010(12):10-12.
[5] 喻桂兰.一种分析时序逻辑电路的补充方法[J].现代计算机(专业版),2012(28):7-10.
YU Gui-lan.A supplementary method for analysis of sequential logic circuits[J].Modern Computer,2012(28):7-10.
[6] 陶文海.状态分配规则及相邻状态链分配技术[J].安徽师范大学学报:自然科学版,2004,27(3):268-272.
TAO Wen-hai.Rules of state assignment and assignment techniques for interlink states chains[J].Journal of Anhui Normal Unirersity:Natural Science,2004,27(3):268-272.
Comparative analysis on several common BCD codes in synchronous sequential logic circuits
YAN Li-qiang, GUO Yu-ping, LIU Chong-xian
( School of Engineering, Tibet University, Lhasa 850000, China)
BCD is also known as binary coded decimal number. According to the actual demands, there are many encoding forms for BCD. If selecting different BCD codes to complete the circuit design, the logic circuit will be showing different structures and working processes. This paper selects a concrete example in synchronous sequential logic circuit to analysis the impact of coding reliability, self-starting capability, the circuit structure and utilization of components by using six different encoding forms of BCD to complete a full design.
BCD code; synchronous sequential logic circuits; weighted code; non-weighted code
TN79+1
A
1674-6236(2014)03-0129-04
2013–06–24 稿件编号:201306154
国家自然科学基金(61261021)
严李强(1980—),男,陕西大荔人,硕士,讲师。研究方向:电子技术基本理论的教学与研究工作。

