基于改进NSGA2算法的配电网分布式电源优化配置

孙建龙，吴锁平，陈燕超

(1.东南大学电气工程学院，南京市210096;2.江苏省电力设计院，南京市211102)

0 引言

人口膨胀和经济快速发展使全球电力需求大幅增长，适用于传统大规模的集中供电方式，如特高压输电网，在近几年加快了建设的步伐。传统大电网具有很多优势，如大机组的投入提高了功率因数，联网的高压输电网降低了存储容量，远距离大功率传输能量可以最大限度地降低网络损耗。但大电网也有自身的缺点:不易灵活跟踪负荷，导致利用率低;系统小范围故障，容易导致大电网崩溃;向偏远山区供电成本高。

分布式电源具有可靠性高、污染少、安装灵活以及能源利用率较高等优点［1］，可以有效地和大型电网进行优势互补，进一步提高供电的可靠性［2-3］，在电力系统改革势在必行的形势下，分布式电源得到了快速的发展。但随着分布式电源在配电网渗透率的提高，对配电网有功网损、电能质量、继电保护、潮流计算等方面造成诸多不利的影响［4］。因此合理优化分布式电源的地点和容量就显得极为重要［5-7］。

文献［8］提出基于向量评估的遗传算法(vector evaluated genetic algorithm，VEGA)，提高了群体多样性，相比简单加权法有优势，但常常收敛于局部解。文献［9］采用小组决胜遗传算法(niched pareto genetic algorithm，NPGA)，可以很快找到最优解集，但需要人为地确定合适的锦标赛规模，从而影响优化精度。文献［10］提出了非支配排序遗传算法(non-dominated sorting genetic algorithm，NSGA)，可以得到非劣最优解集，但其计算复杂度偏大，且需要设置共享参数。

本文建立了以有功网损、电压稳定性指标、投资费用3个目标最小的多目标优化配置模型。提出了一种改进带精英策略的非支配排序遗传算法，可以得到多目标下的Pareto解集，缩短非劣分层所需时间。对算例进行优化分析，结果表明该模型可以较为全面地优化配电网分布式电源的配置。

1 配电网分布式电源优化配置模型

本文针对配电网分布式电源优化配置的问题，主要考虑经济性和安全性两个问题，建立了分布式电源有功网损、电压稳定性指标、投资成本最小为目标的配电网多目标优化模型。

1.1 目标函数

(1)配电网网损。有功网损受分布式电源的安装位置和容量影响，以有功网损最小为目标函数

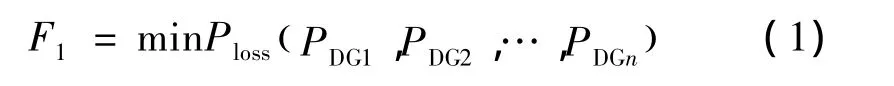
式中:PDGi表示在第i节点安装的分布式电源的有功输出。

(2)电压稳定性指标。根据前推回代潮流计算方程推导了一个2节点的配电网电压稳定性指标L，如图1所示，随后推广到N节点的网络，其表达式为

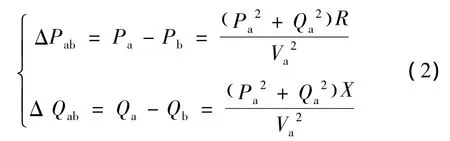
式中:Pa、Pb分别为送端和受端的有功功率;Qa、Qb分别为送端和受端的无功功率;R和X分别为支路上的电阻和电抗;Va为送端电压。

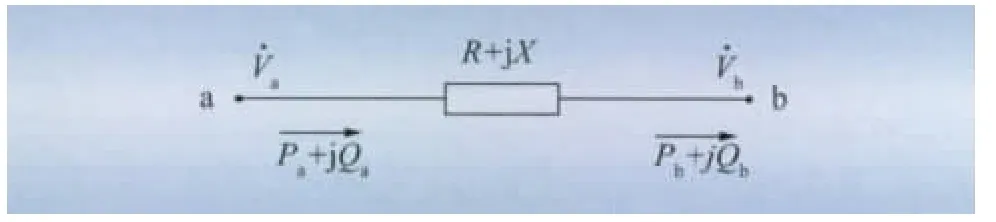
图1 线路功率示意图Fig.1 Line power

以Pa和Pb为变量，式(2)存在实数解的条件是:

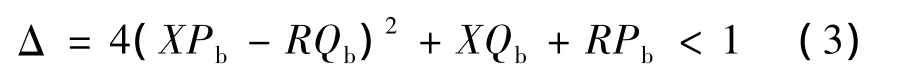
定义电压稳定性指标为

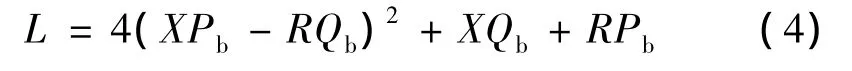
L越小，电压稳定性就越好，相反，当L越大并趋近于1.0时，系统电压越不稳定。

但是上述等值网络的电压稳定性指标没有包含电压参数，将电压参数包含在电压稳定性指标中，这样的模型可以真实地反映原网络:

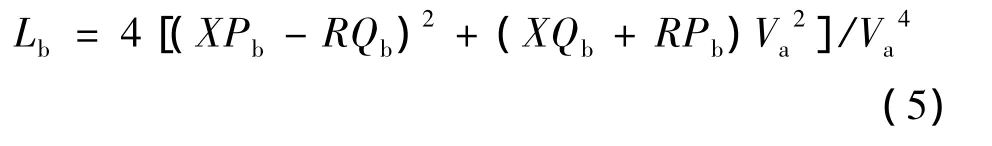
式中:Lb为支路b的电压稳定指标。

找出N个节点系统的电压稳定指标，取所有支路中最大电压稳定指标，即

上述的F2值被称为最薄弱的支路。因为当系统发生电压崩溃时，最薄弱处最容易引发电压崩溃现象。因此可以根据F2和1的接近程度，来判断电压稳定性的问题。

(3)分布式电源投资成本。投资成本主要有以下2个部分:安装容量的成本和安装位置的成本。安装容量成本正比于安装容量大小，安装位置成本与分布式电源安装节点位置的个数有关。

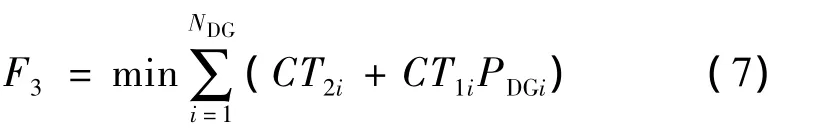
式中:NDG表示能安装分布电源的位置个数;CT1i为第i个节点分布式电源单位容量的投资成本;CT2i为投资地点的综合成本;PDGi为第i个节点安装的分布式电源的容量。

1.2 约束条件

潮流方程

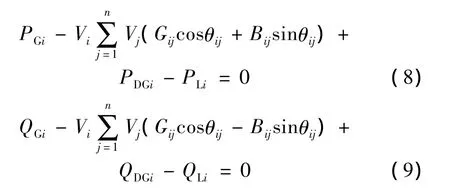
节点有功功率注入约束:

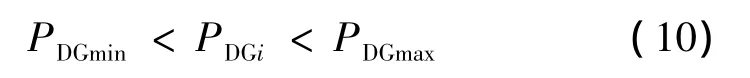
节点电压约束:

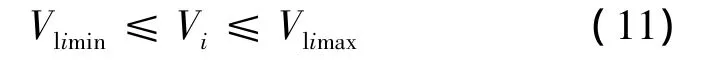
线路传输功率约束:

电压稳定性指标约束:

式中:PGi、QGi分别为传统发电机节点的有功无功输出;PDGi、QDGi分别为新安装的分布式电源的有功输出和无功输出;PLi、QLi分别为线路的有功负荷和无功负荷;Vi、Vj为节点 i、j的电压幅值;Gij为节点 i与节点j之间的电导;Bij为节点i与节点j之间的电纳;V1min、V1max为节点电压的上下限值;Pmin、Pmax分别为分布式电源的有功注入上下限值;Pij为节点i与节点j之间的传输功率;Psmax为传输线路有功的上限值;Lmax为电压稳定性指标的上限。

2 多目标下分布电源优化配置

2.1 改进NSGA2算法

Deb提出的非支配排序遗传算法NSGA在多目标优化中得到了广泛的应用。但是，NSGA计算复杂度较高，缺少保护最优个体的策略，其共享半径需要人为指出。带精英策略的非支配排序遗传算法NSGA2，改进了NSGA的不足，减少复杂度，提出的拥挤度算子无须参数指定，可以保存最优个体。

NSGA2的主要实现过程:首先将初始种群P0进行遗传操作产生子代种群Q0，将父子2代群体合并，进行非劣分层排序。实际上，是对新产生的种群作为整体进行非劣排序，进行精英保留操作，排序分层结束后，取所有前沿中的前N个个体进入下一代父代中，将2代中的优秀个体选择进入下一代。继续循环以上操作，直至达到最大循环代数。在非劣分层排序过程中，对2N个个体都进行了分层排序，在每一个分层结束后都进行拥挤度排序。非劣分层产生的前N个个体被选择进入下一代群体，因此，后N个个体进行非劣分层排序是做无用功，这样加大了程序占用内存和计算时间。本文将单亲遗传算法植入到NSGA2，这样NSGA2继承了单亲遗传算法的优点。其改进后的基本流程如下所示:

(1)随机产生初始种群P0，经过遗传操作产生新的种群Q0，此时令s=0;

(2)合并父代子代种群Rs=Ps∪Qs，对Rs进行非劣排序，得到非劣前沿 F1，F2，…，Fn;

(3)当产生的前m个前沿中的个体总数大于总数N时，停止分层排序。将前m个前沿依次填入下一代中，对第m个前沿先进行拥挤度排序，取最稀疏的个体填至总数至N。

(4)对种群 Ps+1进行复制、遗传操作，形成种群Qs+1;

(5)如果达到终止条件，则退出;否则s=s+1，程序执行(2)。

其实现过程如图2所示。

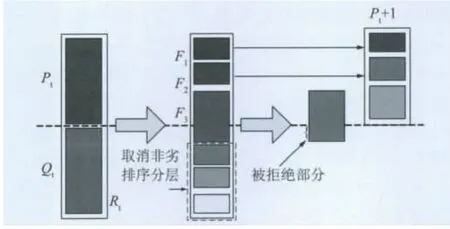
图2 NSGA2主要过程Fig.2 Main process of NSGA2

NSGA2的核心算法是非劣分层排序和拥挤距离排序。

(1)非劣分层排序。对于个体i，找出支配个体i的数量，记作ni;以及被个体i所支配的个体的集合，记作Si;首先，找出ni=0的个体的集合，其对应于第一前沿。对于所属第一前沿的个体，将其Si所包含的个体的ni值减一，并找出ni=0的个体集合，记作第二前沿，依次类推，直到所有个体的非劣排序结束。

(2)拥挤度距离。拥挤距离用来评估一个解周围其他解的密集程度，拥挤度距离的引入是为了保持种群的多样性，防止个体局部堆积。拥挤度距离示意图如图3所示。

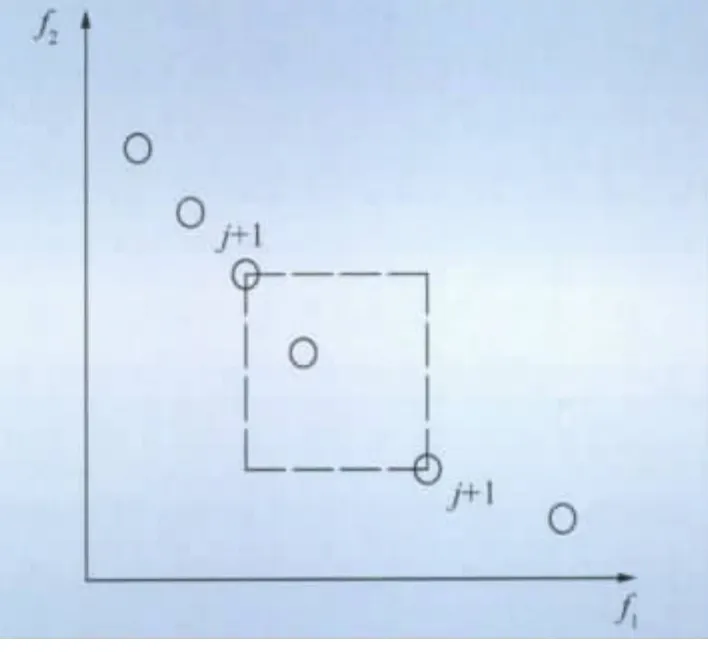
图3 拥挤度距离示意图Fig.3 Crowding distance

首先对每个目标函数所有解的值进行计算并排序。处于边界解的拥挤距离被设为无穷大拥挤距离。其他解的拥挤距离计算如下所示:

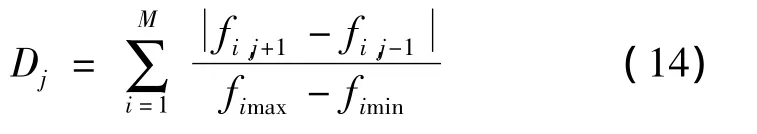
式中:M为目标函数的个数;Dj为第j个个体的拥挤距离;fi，j为第 j个个体在第 i个目标函数的值;fimax、fimin分别为第i个目标函数的最大值和最小值。

2.2 基于改进NSGA2算法的分布式电源优化配置

NSGA2采用实数编码，分布式电源的位置和容量都用十进制整数来表示。本文引入IEEE33节点算例，将分布式电源的位置和容量用一组十进制变量C={C1，C2，Ci，…，C33}表示，其中 Ci表示在节点 i安装分布式电源的容量编码，令PDGi=CiP0，其中P0表示单个分布式电源的容量，若Ci=0表示该节点没有安装分布式电源，若Ci=5表示在该节点安装5P0容量的分布式电源，以此类推。

(1)群体初始化。由于分布式电源总的安装容量不能超过配电网新增负荷的一定比值，并且单节点安装的分布式电源容量也有上限，因此初始化数据时，总安装数量和单点安装数量都应满足约束条件。

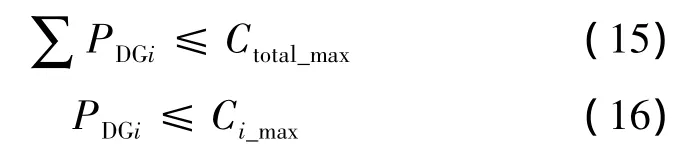
式中:Ctotal_max表示分布式电源安装总容量编码上限;Ci_max表示单个节点分布式电源安装容量编码上限。

(2)变异操作。基因突变时按一定概率Pe2让染色体的一个基因或多个基因发生突变，在突变点上用其他值代替。由于每个点安装容量有上下限，且总安装数量也有上限，因此变异范围需要加以限制。下面用简单算例进行演示。

设分布式电源安装总容量的编码上限为45，单个节点的容量编码上限为15。当前个体安装总容量的编码为40，随机选择，当3号节点被选中，它变异后取值范围只能为0～15。而3号节点的数值由1突变到7，总的安装数量46超过了安装总容量45的限值，因此首先计算此时安装总数与最大安装容量的差值，为45－40=5，因此3号节点的突变范围只能为0～5。

3 算例分析

采用IEEE33节点算例，分布式电源模型简化为PQ型节点，功率因数为0.9。其单个容量 P0=0.003 pu，电 压 约 束 为 0.93 pu ≤ Vi≤ 1.0 pu，max(L)≤0.05;CT1i和CT2i分别设为0.2万元/MW、0.8万元/MW;取12.66kV为电压基准值，10MW为功率基准值。以有功网损最小、电压稳定性指标最优、投资费用最小为多目标函数，采用NSGA2来优化分布式电源的配置。优化结果如图4所示。

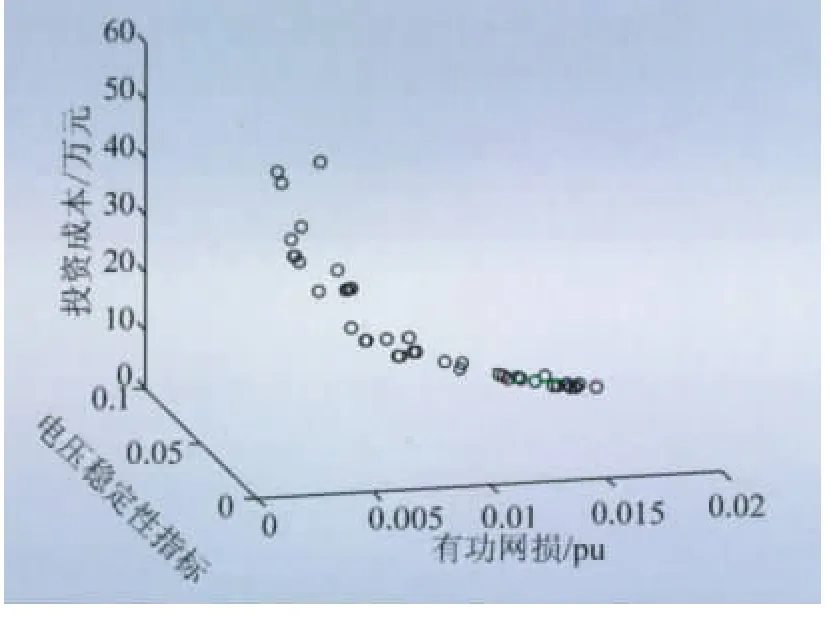
图4 NSGA2的优化结果Fig.4 Optimization results of NSGA2

图4 标示的点集为第一前沿的非劣解集，由于在三维下分析不便，下面将三维图分别投影到双目标所组成的平面上，结果如图5所示。

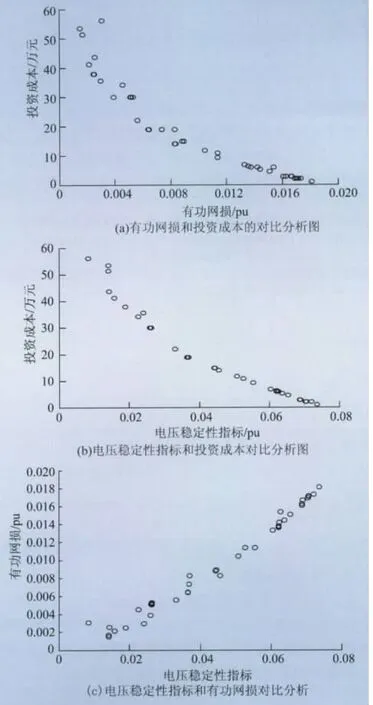
图5 双目标对比分析Fig.5 Bi-objective comparative analysis

由图5(a)、(b)可知，分布式电源投资成本越大，配电网网损越小，电压稳定性指标越小。投资成本较小时，电压稳定性指标和有功网损值较大。从图5(c)可得，电压稳定性指标和有功网损没有明显矛盾关系。一般而言，网损减小会伴随着电压稳定性指标降低。

从非劣解集中取3个解进行对比分析，结果如表1所示。从表1可得，方案A投资成本最小，但是有功网损和电压稳定性指标改善不大;方案C，有功网损和电压稳定性指标最小，但分布式电源的安装容量较大;方案B兼顾了3个目标函数，虽然3个方案都不能使各个目标达到最优，但是，相比未装分布式电源时，有功网损降低和电压稳定性指标都减低很多。

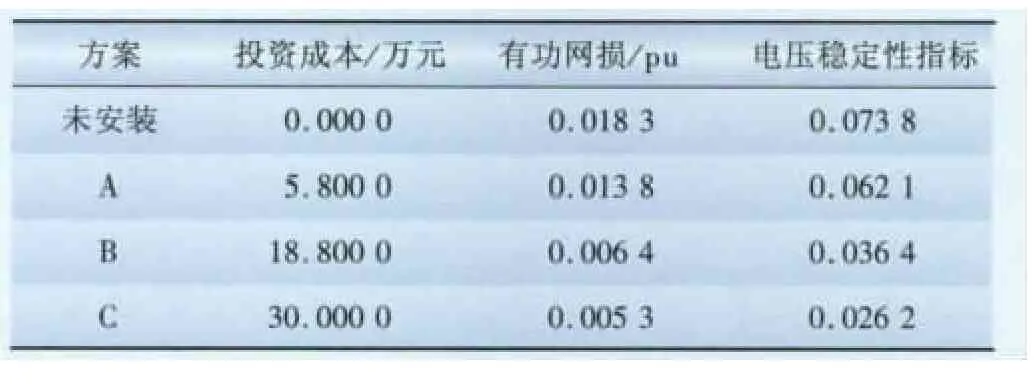
表1 分布式电源配置优化结果Tab.1 Optimization result of distributed generation configuration

采用方案B，其分布式电源的配置如表2所示。

表2 分布式电源配置优化结果(单个容量P0=0.005 pu)Tab.2 Optimization result of distributed generation configuration(single capacity P0=0.005 pu)

4 结语

本文考虑分布式电源有功网损、电压稳定性和投资成本，建立了配电网多目标优化配置模型。并提出了一种改进带精英策略的非支配排序遗传算法，可以得到多目标下的Pareto解集，缩短非劣分层所需时间。对算例进行优化分析，结果表明:

(1)接入分布式电源可以有效减少有功网损，降低电压稳定性指标;

(2)采用改进NSGA2的优化方法，可以给出多个优化配置方案，这些方案都是最优解，每个方案都兼顾了3个目标函数，尽可能使多目标都趋近最优，发挥分布式电源配置的最大效益。

［1］王建，李兴源，邱晓燕.含有分布式发电装置的电力系统研究综述［J］.电力系统自动化，2005，29(24):90-97.

［2］张传铨，张焰.计及分布式电源的配电网供电可靠性［J］.电力系统自动化，2007，31(22):46-49.

［3］王敏，丁明.分布式发电及其效益［J］.合肥工业大学学报，2004，27(4):354-358.

［4］王成山，王守相.分布式发电供能系统若干问题研究［J］.电力系统自动化.2008，32(20):1-4.

［5］Carmen L T，Djalmam.Optimal distributed generation allocation for reliability，losses，and voltage improvement［J］.Electrical Power and Energy Systems，2006(28):413-420.

［6］钱科军，袁越.分布式发电对配电网可靠性的影响研究［J］.电网技术，2008，32(11):74-78.

［7］王成山，陈恺，谢莹华.配电网扩展规划中分布式电源的选址和定容［J］.电力系统自动化，2006，30(3):38-43.

［8］Rekha T J，Ghadir R.Modeling and control of distributed generation systems including PEM fuel cell and gas turbine［J］.Electric Power System Research，2007(77):83-92.

［9］Horn J，Nafpliotis N.Multi-objective Optimization using the Niched Pareto Genetic Algorithm［R］.Technical report IlliGAI report 93005， University ofIllinois atUrbana-Champaign，Urbana，Illinois，USA，1993.

［10］Srinivas N，Deb K.Multi-objective Function Optimization Using Non-dominated Sorting Genetic Algorithms［J］.Evolutionary computation，1995，2(3):221-248.