平行四边形为什么不是轴对称图形

徐建

在教学完“轴对称图形”这一单元后，学生总有一个绕不开的图形：平行四边形。因为是常见图形，很多学生特别容易认为它是轴对称图形，对称轴是对角线所在的直线。

为什么总有学生认为平行四边形是轴对称图形呢？是不是在教学中忽略了什么？阅读相关资料后发现，对称图形，除了轴对称图形（线对称）以外，还有中心对称图形（点对称）。平行四边形就属于中心对称图形。苏教版小学数学教材中只安排在三年级下册和四年级下册认识轴对称图形，教学目标分为两个阶段：三年级安排认识轴对称图形，四年级安排学生画轴对称图形的对称轴，学生出现认识错误开始于三年级，教材P.56对轴对称图形的定义是“对折后能完全重合的图形是轴对称图形”，“试一试”（苏版P.57）中也出现了平行四边形，教材几乎都是由学生动手操作来感受轴对称图形的，这就出现了一个问题：动手操作能否代替理性思考？不能！那么动手操作对概念的建立有什么影响呢？三年级时学生只需要从实物中抽象出图形并判断是否是轴对称图形，充其量只是初步感知轴对称图形的特点，而到了四年级学生在原有的知识基础上需要画对称轴时，就必须考虑如何不经过动手操作就可以体现这个图形的对称性。这正是很多教师忽略的一点。

为此，我在教学四年级下册《轴对称图形》时，加入了理性思考的过程。具体内容如下：

师：同学们，平行四边形沿着对角线剪开，得到的两个三角形有什么特点？

生：形状相同。

师：形状相等的图形就能完全重合么？（动手演示：一个三角形旋转180度和另一个三角形重合）

生：不能，不能旋转。

师：除了形状相同以外还需要什么条件？

生：方向要相反。

师：形状相同，方向相反，不能旋转。那凭什么认为平行四边形是轴对称图形呢？

有个别学生喊出了“凭感觉”。

师引导：数学学习不能光凭感觉来判断，还需要理性思考。对平行四边形必须这样。想一想，如果不经过动手操作，如何判断是不是轴对称图形呢？

学生陷入思考。

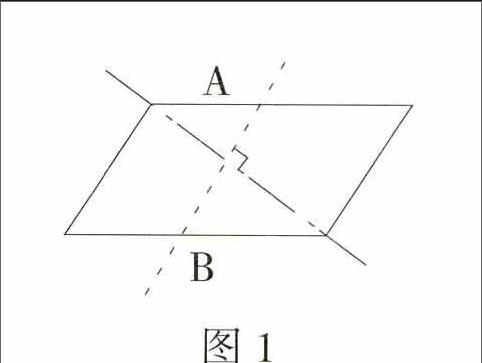
师：如何证明这一点和这一点能完全重合呢？我们可以用“垂线检验法”。（演示：画一条“对称轴”的垂线，将交点标为A和B，如图1。）

想一想，A点和B点到垂足的距离是否一样？不一样的话能否完全重合？

学生立刻明白：两边不能完全重合。由此认为被分成的两个部分也不一样。

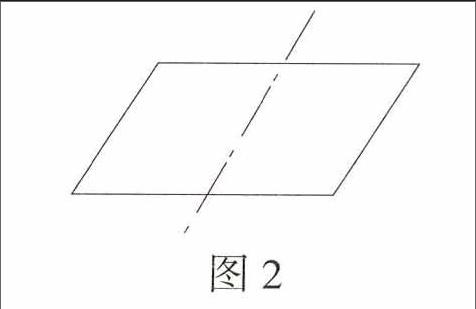
师：如果这样呢？（如图2请同学们动手画一画。

小学数学的知识和结论很多时候缺少严谨的推理和论证，更多是所谓的“合情推理”，长期以来造成了学生做题喜欢“凭感觉”而缺乏理性思考，而恰恰是这种“凭感觉”使得学生容易被明显特征所吸引，而忽略了理性思考。教师在面对这种现象时，要积极引导学生进行理性思考并适当安排变式教学，引导学生针对概念的外延进行拓展和挖掘，为全面掌握知识建立良好的思维基础。

【责任编辑：陈国庆】