超声谐振器在传感器测距中应用分析*

东鑫渊， 谷立臣， 琚晓涛

(西安建筑科技大学 机电工程学院，陕西 西安 710055)

0 引 言

在远距离超声测量时，由于空气的吸收损耗和几何扩散损失，使超声回波信号随着距离的变化，信号幅度的波动很大，且很微弱，回波等待过程中，会混入大量杂散回波和收发电路的电噪声干扰信号。背景噪声较为严重时，回波有用信息较为微弱，系统难以识别目标有效回波信号位置，常常造成误判。为了克服该系统中超声传感器声辐射效率低和辐射场波束角较大，回波信号信噪比低，从而导致测距范围和精度有限等实际问题[1～3]。本文设计了一种超声谐振器，通过机理分析阐明超声谐振器对改善阻抗匹配，影响声源指向性的重要设计参数，通过改变这些参数可以提高声辐射效率，使指向性尖锐，能量更集中，从而有效提高了超声传感器的测距范围和精度。

1 超声谐振器对声辐射能量影响

本文将谐振器看作是一种截面连续变化有限长管子，主要用于增加声源处辐射。谐振器可以给声源任意声阻抗，在大开口端实现与空气平面波阻抗有效匹配，进而可以提高声音的辐射效率。通过声波在截面连续变化的管中传播规律和声波动方程等理论分析来说明。设谐振器截面积是关于坐标x的函数，声辐射的波阵面按截面尺寸S=S(x)变换，声传播规律遵循基本声波动方程基本形式[4]

(1)

式中p为声压，p=p(x)ejωt，c0为声速,且解为：p(x)=A(x)e±jγx。

本文以指数形谐振器为例，其截面变化规律为S(x)=S0eδx,S0为谐振器喉部面积，δ为蜿展系数，表示截面积变化快慢。在某一x位置截面半径用r表示，如图1所示。根据截面曲线可得谐振器声压一般表达式

(2)

图1 超声谐振器示意图

=Ra(x)+jXa(x).

(3)

(4)

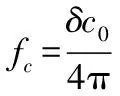
(5)

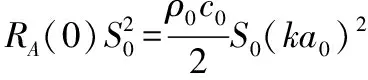
(6)

其中，活塞辐射中ka0<0.5[4]。对比式(5)、式(6)可知未加谐振器损耗功率比加装谐振器要小得多。

因此，在声源前加上谐振器，相当于给声源匹配了“合适”声阻抗，提高声辐射效率和辐射能量，有利于超声波在远距离探测中应用。同时，在设计中可以改变谐振器外形、尺寸参数、截面曲线变化等控制声辐射场能量分布。

2 超声谐振器对声指向性影响

声束集中向一个方向辐射性质叫做声场指向性。声场指向性通过声束指向性因数D表示，指向性因数D越大，声源指向性越尖锐。声源辐射指向特性是指在谐振器形成的远声场中，当距振源中心r时，偏离中轴线某个角度θ方向上的声压幅值pθ与θ=0°轴上的声压幅值p0的比。指向性控制是延长声波测距的另一个重要手段，控制了指向性就是控制衰减特性和传输距离。

2.1 利用Bessel函数分析对指向性影响因素

谐振器内声波可近似为平面波，对于一个有限尺寸谐振器可以假设其声阻抗与一个安装在无限大障板上活塞声阻抗一样，同时其辐射指向性也是近似为活塞式声源指向性[5]。当活塞以速度u=uaejwt沿平面法向方向振动，假设活塞半径a，在活塞上取一个距活塞中心q的面元dS，如图2所示。由于要实现谐振器远距离辐射，因此,其声场传播遵循远声场特性，则将面元看作一点声源，整个谐振器声场是由多个点声源叠加构成。所有点源声波辐射叠加理论就是对面元dS积分。在无限空气场中任取一点P，对于远距离声场中极径ρ≪r，h为面元到P点距离，由几何关系h=r-ρcos(ρ,r)。根据叠加积分法可得观察点P处辐射声压

(7)

式中 面元dS=ρdρdφ，则积分

(8)

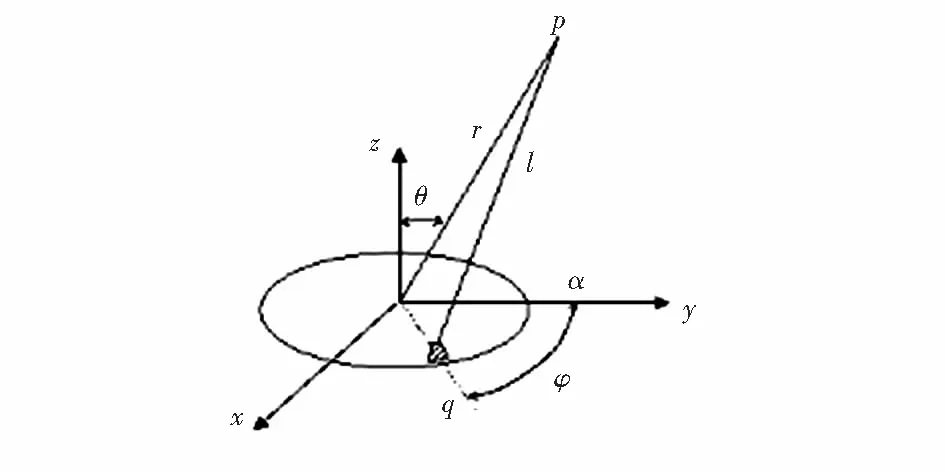
图2 圆形活塞辐射声场

Bessel函数是柱坐标或球坐标下使用分离变量法求解拉普拉斯方程和亥姆霍兹方程时得到的。Bessel函数主要解决波动问题和各种涉及有势场的问题，常见典型问题有：圆柱形波导中电磁波传播问题；热传导问题；声学中声场传播问题。在研究声场时，先根据零阶Bessel函数定义如下关系

(9)

(10)

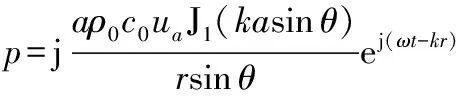
根据一阶Bessel函数另一个性质：当x=0时，J1(x)/x=1/2，所以谐振器声指向性因数

(11)

由式(11)得，D(θ)越大，ka乘积就要越大。ka=2πa/λ，这说明声源的指向性与谐振器半径和辐射声波波长相对比值有关，声波波长与声源频率大小有关。因此，指向性尖锐程度取决于声源频率，谐振器开口面积，开口面积取决于壁面曲线方程。

2.2 超声谐振器声辐射仿真计算

本文以声场计算的可视化角度，利用Matlab提供画图功能函数，参考指向性因数方程和一阶Bessel函数条件下的远场声压方程，模拟超声探测过程中不同参数谐振器和声源频率，即不同ka取值对声场指向性影响和辐射声场分布。图3和图4分别表示ka=1,ka=π，ka=2π，ka=4π对应的指向性图和辐射声场随时间变化三维分布图。

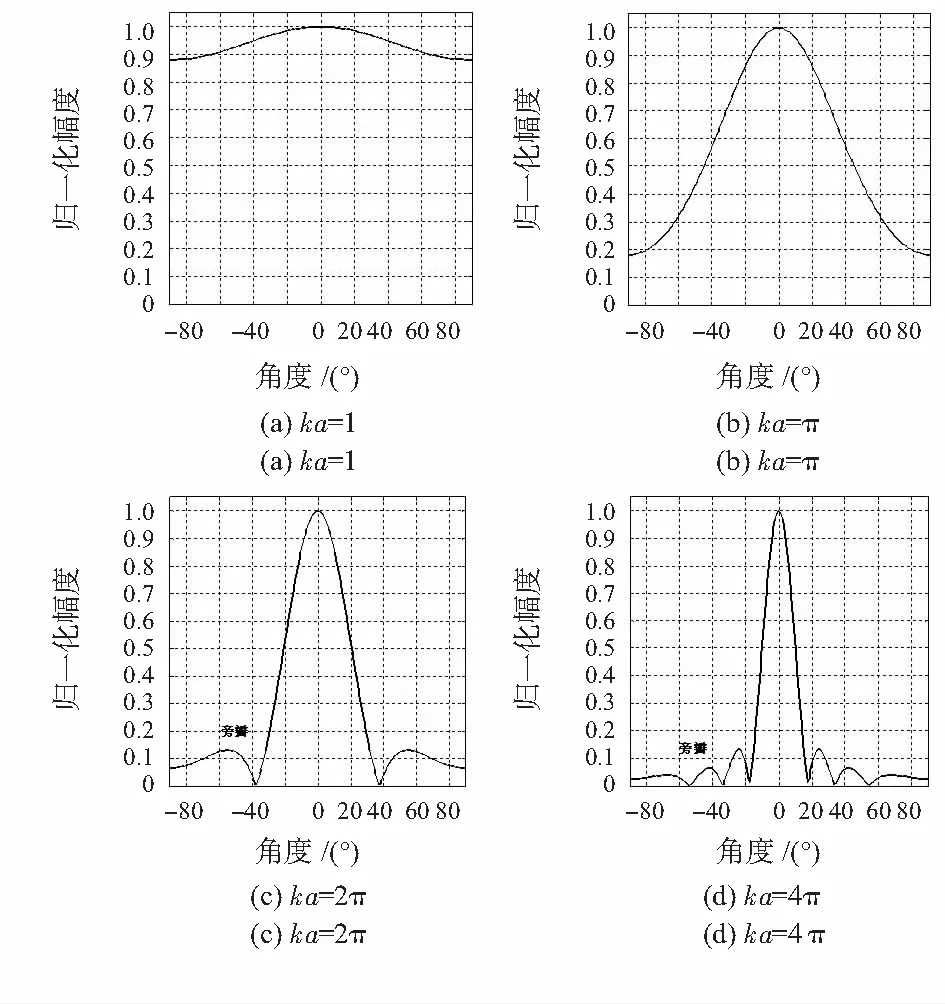
图3 不同参数指向性图

图4 不同参数辐射声场三维分布图

从图3可看出:随谐振器出口半径不断变大，或随声源频率不断提高，声指向性越来越尖锐，且由图3(c)，(d)还可看出：旁瓣辐射强度不断减弱(旁瓣消耗声源能量)。由图4得到声场分布图和最大声压值，分别为：0.62,0.78,0.83,0.90，声压值大小可以间接表示声传播过程的能量变化。因此，有谐振器的传感器开口面积会间接变大几倍，有利于声能量集中，辐射效率的提高。

此外，声波在传播过程中衰减系数：α=Ae·f2,其中，Ae为介质常数；f为声源频率。由公式可知，声源频率越大，衰减越严重，传播距离越小 。但是声源频率越大，谐振器开口越大，指向性越尖锐。因此，对大量程测距提高效率分析中，既要考虑指向性问题又要兼顾声衰减问题。综上，应选用传感器声源频率低和开口面积大的系统，开口面积就可通过加设谐振器实现。

3 谐振器实验验证

本文采用的实验装置如图5所示，其中,收发换能器频率均为40 kHz，最大测距为8 m。

通过发射超声脉冲信号，将障碍物(墙体)反射回波信号由放大电路放大，采集最终放大回波信号。由于实验场地限制，分别取5,6,7 m进行实验，通过对比换能器未加谐振器与发射或接收换能器加谐振器回波幅值的大小进行验证。

图6是在距传感器6 m，放大20倍时障碍物反射回波图：图6(a)未加谐振器，图6(b)发射传感器加谐振器，图6(c)接收传感器加谐振器。表1为不同探测距离所对应最大电压回波幅值。

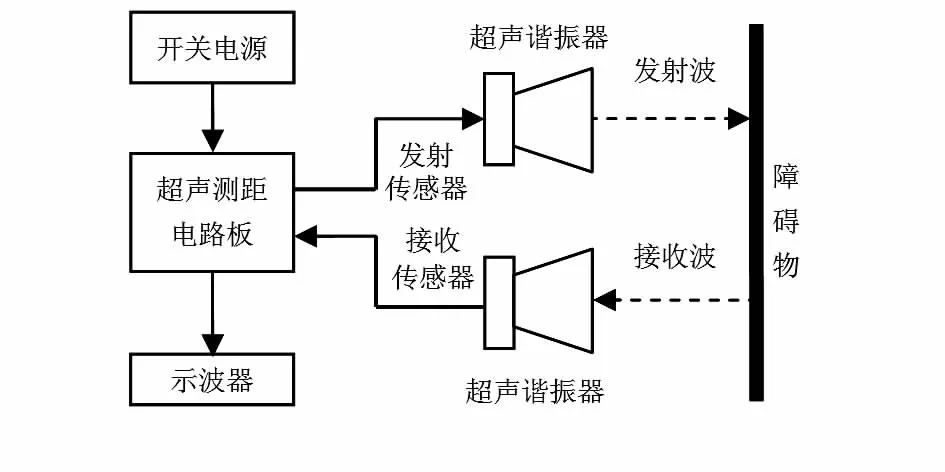
图5 实验验证装置

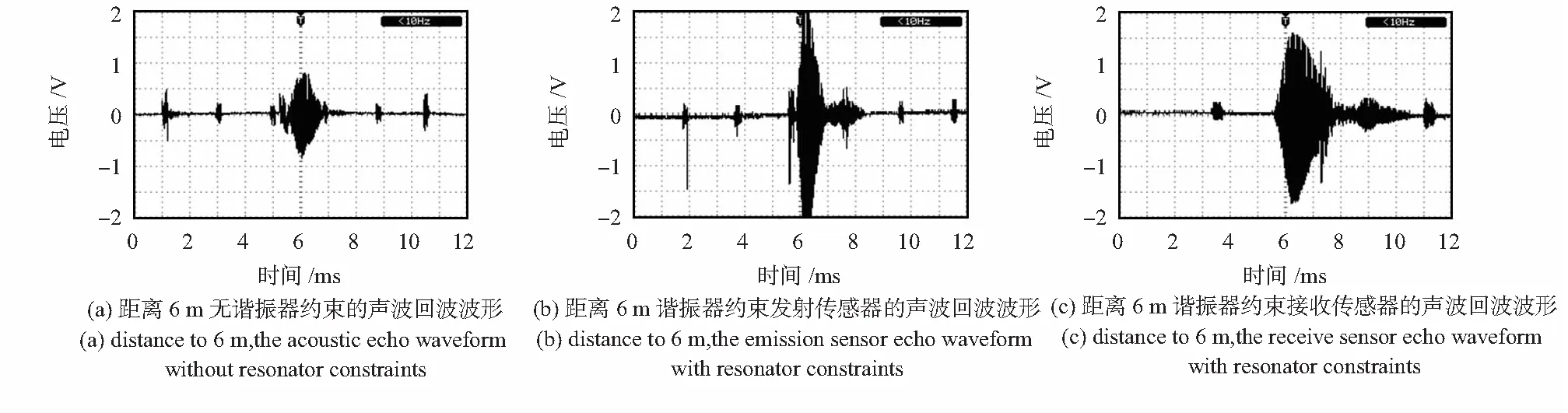
图6 距离6 m时谐振器在换能器测距中作用效果

表1不同距离下的最大电压回波幅值

Tab1Themaximumvoltageechoamplitudeindifferentdistance

测量距离(m)电压回波幅值未加(V)电压回波幅值发射加(V)电压回波幅值接收加(V)53.568.249.6062.044.763.6271.123.803.56

从图6和表1可以看出：随着探测距离增大，回波幅值不断减弱；且无论在发射或接收传感器前加谐振器对声波进行约束，均可使声能量集中，使电压回波幅值明显提高。因此，谐振器有利于改善声辐射效率，提高测距量程。

4 结束语

本文分别从理论分析、模拟计算和实验验证角度研究了在传感器前面加设超声谐振器对声场辐射效率、能量分布和指向性对声传播距离的影响，得出了影响声源指向性的重要设计参数、优化声源频率，开口面积等设计参数对提高超声辐射效率和远程测距的意义。本文说明了超声谐振器一方面可以给声源匹配合适声阻抗，较大幅度提高声功率和声辐射效率；另一方面，可以改善声指向性尖锐程度和声辐射效率，使声辐射能量集中，有效提高了超声传感器的测距范围和精度。

参考文献:

[1]寇雪芹,谷立臣,闫小乐,等.基于虚拟仪器的超声信号测量与测距研究[J].计算机工程与应用,2012,48(6):17-20.

[2]Yan Xiaole,Gu Lichen.Time-delay estimation of ultrasonic echoes based on the physical model matching[C]∥8th IEEE International Conference on Automation Science and Engineering,2012:72-78.

[3]陈先中,王 伟,张 争,等.低噪声回波测距系统的电路设计与系统分析[J].北京科技大学学报,2005，27(4):488-492．

[4]杜功焕,朱哲民,龚秀芳.声学基础[M].南京:南京大学出版社,2009.

[5]么 启,刘纪元.一种大量程超声波液位计的实现[J].电子设计工程,2011(22):57-61.

[6]潘仲明.大量程超声波测距系统研究[D].长沙:国防科技大学,2006.