基于GMS摩擦模型的机器人低速运动研究*

靳兴来，朱世强，吴文祥

(浙江大学 流体动力与机电系统国家重点实验室，浙江 杭州 310027)

0 引 言

在伺服系统中，摩擦是一种难以避免的、复杂的非线性扰动因素[1]，摩擦力严重制约了机器人的低速运动性能。由于摩擦的非线性，其影响主要表现在：在低速跟踪时，存在“滞滑”现象，产生静态误差，影响跟踪和定位精度；速度过零时，由于摩擦力的不连续变化，导致出现波形畸变。文献[2]中分析了低速运动时的爬行现象，指出了摩擦力作为主要干扰因素所造成的影响。文献[3]指出由于摩擦力的强非线性，通过线性反馈控制系统只能部分地减弱摩擦力的影响。因此,基于模型的摩擦力补偿对于低速控制是十分有效的方法。然而，目前针对摩擦问题的研究多集中于常速状况，忽略了低速运动研究的意义。近来，倪风雷等人[4]将GMS(generalized Maxwell-slip)模型应用在拖动系统中，低速控制效果明显。

本文为了提高机器人关节的低速运动性能，减小轨迹跟踪误差，进行了基于GMS摩擦模型前馈补偿的相关研究，为了将前馈补偿引入机械手控制系统，设计了电机的力矩控制系统。

1 GMS摩擦模型

1.1 摩擦机理

通过对摩擦力机制的深入研究，人们逐渐发现摩擦力存在2种机制：预滑动机制和滑动机制。在预滑动阶段，基于位移的粘性摩擦力起主要作用，因此,摩擦力表现为微变形的关系式,随着微变形量的增加，最终会产生滑动。在滑动阶段，摩擦力与速度相关[5]。文献[6]指出了目前应用较广的摩擦模型存在不能辨识预滑动阶段摩擦力的缺点，通过实验对比，验证了GMS模型在低速控制时的优点。

GMS模型能够描述摩擦的3个基本现象：常速状态下的Stribeck效应；预滑动阶段的不具有局部记忆的滞回效应；滑动阶段的摩擦记忆。

1.2 GMS模型表达式

目前实用的摩擦模型多是基于一个摩擦力方程和一个状态方程的，而GMS模型则通过引入一个含系统变量的状态方程来更加全面地描述摩擦力[7]。文献[8]指出GMS模型是一种具有物理假想意义的摩擦模型，它假想为包含若干个状态单一的并联摩擦单元，这些单元包含相同的输入，即速度v，总的摩擦力可看做是所有单元状态输出的综合。考虑粘性摩擦的情况下，其数学表达式如下

(1)

式中N为并联的基本摩擦单元数量；Fi为单个摩擦单元的摩擦力；σ为粘滞摩擦系数；v为速度。其中，每个单元的动态摩擦力Fi由以下微分方程给出：

1)当摩擦单元i处于粘滞状态时，状态方程为

(2)

式中ki为单元的刚度系数。粘滞状态维持至Fi>αis(v)，其中，αi为常数,s(v)为模型的Stribeck曲线。

2)当摩擦单元i处于滑动状态时，状态方程为

(3)

式中αi为单元的权值系数，决定了每一单元停滞状态时的力Fi的最大值；C为常数，决定了GMS模型摩擦力在滑动区域收敛于Stribeck曲线的程度。因此,Stribeck曲线的辨识精度能够影响GMS模型在滑动状态时的控制效果，滑动状态维持至v接近0。s(v)的表达式如下式

s(v)=(Fc+(Fs-Fc)e-|v/vs|δ)sgnv+σv,

(4)

式中Fc为库伦摩擦力；Fs为最大静摩擦力；vs为Stribeck速度；δ为一指数项，在0.5～2之间取值；σ为粘性摩擦系数。

2 实验平台

为了得到GMS模型在实际应用领域的控制效果，基于自主研制的六自由度机械手平台进行实验，实验平台如图1。该机械手采用上位机+下位机的控制架构，上位机为工控机，下位机是DSP+CPLD架构的多轴运动控制卡，本文的控制算法即在下位机中实现。为了能够避免重力、惯性力等因素对模型参数辨识带来的干扰，选择机械手的第一关节进行匀速实验,如式(5)

(5)

式中J为等效到电机上的等效转动惯量；T为驱动力矩；Tf为负载力矩，主要是摩擦产生的阻力矩。

图1 六自由度机械手

3 实验设计

3.1 Stribeck曲线参数的辨识

目前常用的离线参数辨识方法有最小二乘法、非线性回归方法等。由于摩擦本身是一个复杂的非线性现象，它与负载大小、运动速度、环境温度、机械结构等因素有关，所以，用经典的系统辨识方法很难得到比较准确的摩擦模型参数。由于遗传算法具有不依赖于被控对象的精确数学模型、适合在线学习等特点[9]，因此,采用遗传算法进行参数辨识。设计机械手第一关节的控制电机在速度区间[-700,700]r/min匀速运行。具体步骤为：±5～±50 r/min期间以±5 r/min的递增；±50～±100 r/min期间以±10 r/min递增；±100～±400 r/min期间以±20 r/min递增；±400～±700 r/min期间以±50 r/min递增。式(4)中当δ=2时，为Tustin模型，设置遗传算法的种群规模为100，遗传代数为25 000，设置目标函数为式(6)，个体适应度为式(7)

(6)

fm=1/Lm,m=1,2,…，M,

(7)

式中H为所采样速度的个数；M为种群规模；ei为个体i的误差。当交叉概率为0.9时,可以得到辨识结果如图2。

含δ的辨识与Tustin辨识模型的误差对比如图3，Tustin模型辨识误差小且模型简单。

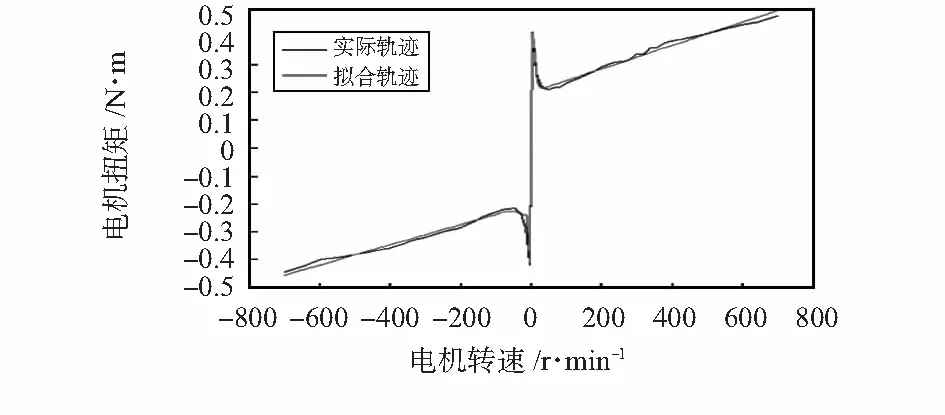
图2 轨迹拟合

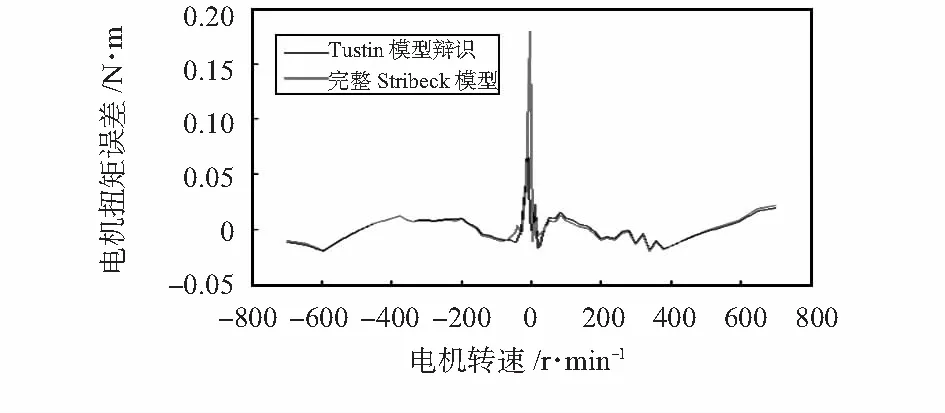
图3 辨识误差对比

辨识得到的模型参数如表1。

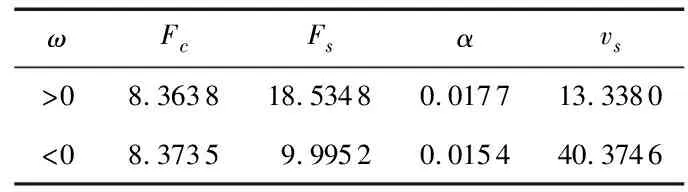
表1 Stribeck模型参数

3.2 粘滞曲线参数辨识

为了辨识预滑动摩擦力的参数，需要得到粘滞曲线。由于粘滞摩擦力决定于摩擦单元的状态变量，状态变量不能直接测量，但是却可以通过运动状态估计得到。文献[5]中指出，可以设计一个周期性运动，使得伺服系统做周期运动并且要保证处在预滑动状态。本文设计了具有较小幅值的做匀速周期运动的轨迹，如图4。

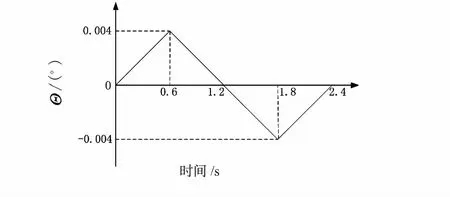
图4 关节运动轨迹

设置伺服驱动器在力矩模式下控制电机，通过下位机实现关节运行图4的轨迹，可得到扭矩—转角图。由于存在噪声等干扰信号，因此，设计了低通滤波器，一阶低通滤波器如式(8)

(8)

式中T为时间常数。

本文采用其离散形式，如式(9)

Yn=λXn+(1-λ)Yn-1,

(9)

式中Xn为本次采样值，Yn-1为上次滤波输出值，Yn为本次滤波值，λ为滤波系数。

滤波效果如图5。

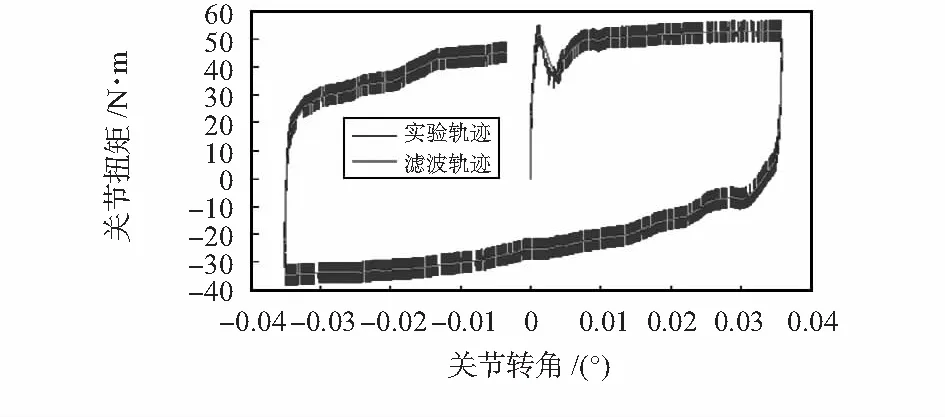
图5 预滑动轨迹

3.3 GMS模型参数辨识

通过图5两组曲线，就可以得到GMS模型。文献[10]中指出，预滑动曲线可近似看做分段曲线，而第一个上升阶段的分段曲线决定了模型的特征状态。其方法是在第一段内取5个状态点P0～P5，分别为P0(0,0),P1(0.004 903,42.79),P2(0.008 535，49.56),P3(0.020 2,51.68),P4(0.035 5,52.95)，由于电机减速比为121，可以转化为电机所对应的5个点。参考文献[3]中的方法，可以得到各线段的斜率为ko=0.596 0 N·m/(°)，ka=0.127 4 N·m/(°)，kb=0.012 4 N·m/(°)，kc=0.005 7 N·m/(°)，同时利用式(10)，可以求得式(2)中的系数ki

(10)

最后，利用式(11)求取权值系数αi

(11)

式中j为还处于粘滞摩擦状态的单元；ΔP=Pi-P0，表示滑动临界点的相对位移；kj为由分段函数确定的比例系数。

通过以上分析，可辨识得到GMS模型所需要的参数，如表2。

4 实 验

利用上述的辨识结果，在机械手第一关节控制系统中分别将GMS摩擦模型、Stribeck摩擦模型作为补偿项引入。速度通过电机自带的编码器反馈得到，并经过低通滤波器滤除噪声干扰。控制原理如图6。

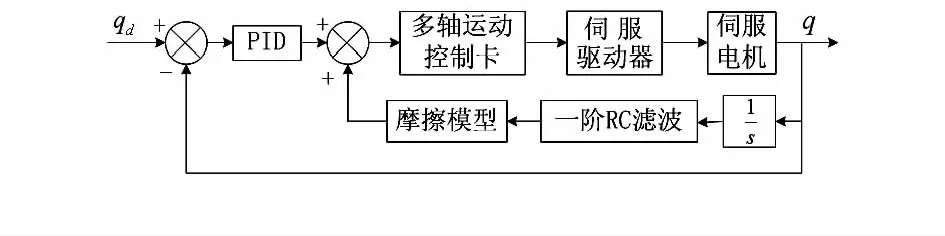
图6 控制系统原理图

为了充分验证模型的作用，设计的跟踪轨迹为关节低速下的大范围运动如图7，得到跟踪误差对比如图8。

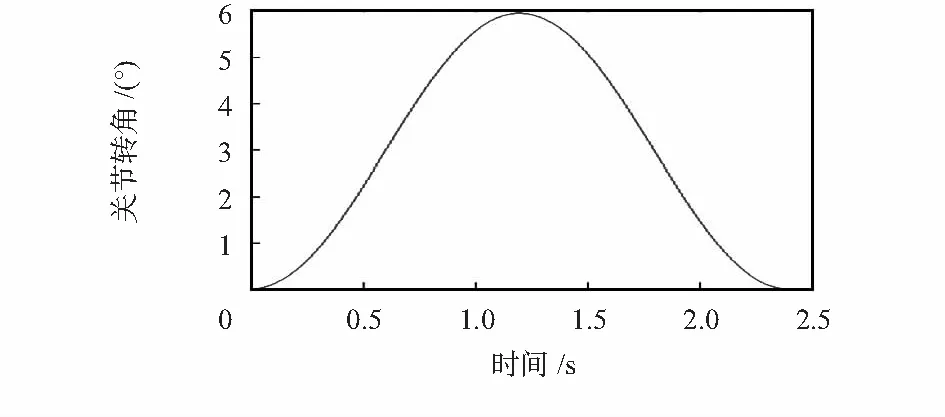
图7 跟踪轨迹

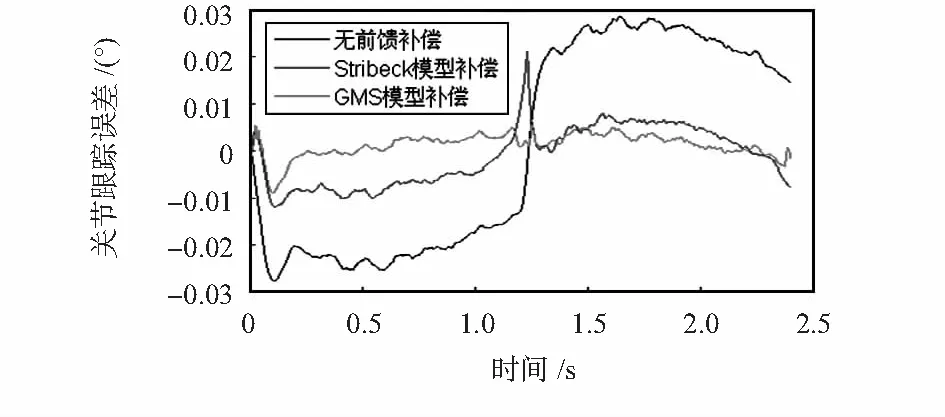
图8 跟踪误差对比图

通过图8可以直观地分析出：

1)当只有普通的PID控制而无前馈补偿时，机械手轨迹跟踪误差为0.28°。

2)加入本文辨识的Stribeck模型作为前馈补偿后，轨迹跟踪误差显著减小至0.012°，但是在起止位置和换向位置处，存在较大误差，尤其是换向位置存在突变。

3)加入本文辨识的GMS模型作为前馈补偿后，误差进一步缩小，并且消除了换向位置处的误差突变，整体的控制效果更优。

5 结 论

针对机械手低速应用场合的不断拓展，本文分析了影响低速运动性能的主要干扰源，鉴于当前对机械手关节摩擦补偿方法仍为传统的Stribeck,LuGre等模型，而这些模型并不能准确描述预滑动阶段的摩擦特性。本文介绍了能够全面描述摩擦特性的GMS摩擦模型，详细讲述了模型的参数辨识和应用方法。最后，通过对机械手第一关节运动的前馈补偿控制，验证了该模型的有效性。

参考文献:

[1]周金柱，段宝岩，黄 进.LuGre摩擦模型对伺服系统的影响与补偿[J].控制理论与应用，2008，25(6):990-994.

[2]李 强.并联电液伺服六自由度平台系统低速运动研究[D].杭州：浙江大学，2008:5-8.

[3]Jamaludin Z，Van Brussel H，Swevers J.Quadrant glitch compensation using friction model-based feedforward and an inverse-model-based disturbance observer[C]∥Proceedings of the 10th IEEE International Workshop on Advanced Motion Control，Trento，2008:212-217.

[4]倪风雷，刘 宏，介党阳.基于速度观测器的GMS摩擦模型辨识与补偿[J].电机与控制学报，2012，16(11)：70-75.

[5]Lampaert Vencent,Al-Bender Farid,Swevers Jan.A generalized Maxwell-slip friction model appropriate for control purposes[J].Physics and Control，2003，4:1170-1177.

[6]Lampaert V,Swevers J,Al-Bender F.Experimental comparison of different friction models for accurate low-velocity tracking[C]∥Proceedings of the 10th Mediterranean Conference on Control and Automation，Lisbon,Portugal，2002.

[7]Al-Bender Farid,Lampaert Vincent,Swevers Jan.The generalized Maxwell-slip model:A novel model for friction simulation and compensation[J].IEEE Transactions on Automatic Control，2005，50(11)：1883-1887.

[8]Lampaert Vincent ,Swevers Jan ,Al-Bender Farid.Comparison of model and non-model based friction compensation[C]∥Procee-dings of the 2004 American Control Conference，Boston，2004： 1121-1126.

[9]刘金琨.机器人控制系统的设计与MATLAB仿真[M].北京：清华大学出版社，2008：615-627.

[10] Ruderman Michael.Modeling and identification of elastic robots joints with hysteresis and backlash[J].IEEE Transactions on Industrial Electronics，2009，56(10):3840-3847.