交互多模型扩展卡尔曼滤波算法的FPGA实现

,

(清华大学 自动化系,北京 100084)

0 引 言

目标跟踪(target tracking)利用探测器对运动目标的某些参数进行测量，以此确定关注区域内目标个数、位置以及运动参数等状态,其在国防与民用领域均有重要应用价值[1]。根据探测器是否主动发射信号，又可分为主动跟踪与被动跟踪。在被动跟踪方法中，纯方位角度跟踪因其具有隐蔽性，备受各国军方重视。

纯方位角度跟踪利用单站测向设备测量目标的运动方位信息，并用这些方位信息序列来实时估计目标轨迹[2]。目标跟踪的经典方法有卡尔曼滤波(KF)、扩展卡尔曼滤波(EKF)以及粒子滤波(PF)等。交互多模型扩展卡尔曼滤波(IMMEKF)算法[3]是多模型算法中的一种经典算法，其基本思想是建立一个由若干模型组成的模型集，目标以一定概率符合某个运动模型。各模型均采用EKF算法进行滤波。IMMEKF算法具有一定的非线性处理能力，且运算速度较快。

当前，对于纯方位角度跟踪问题的研究大多集中在算法和仿真方面[4～6]，对于算法的硬件实现方面的研究则较少。而实际应用中，大量的移动平台亟需准确度、实时性均高的跟踪算法。将跟踪算法硬件化，乃至设计出专用处理芯片是目标跟踪领域的一个重要研究方向。现场可编程门阵列(field-programmable gate array,FPGA)是一种拥有大量计算和存储资源的高性能芯片，其最大的优点是可以通过可重复配置快速实现设计验证。硬件算法如果要转化成专用处理芯片，可以先通过FPGA验证其设计的正确性。文献[7]对数种PF算法进行了修改，提出新的重采样方法，以期得到适于硬件实现并提升处理速度的结构。同时，提出了一种分布式PF结构，提高了滤波器的可扩展性。文献[2]针对纯方位角度跟踪问题提出了一种简化的PF算法，并给出了FPGA上的实现方法。但是，上述研究都是基于单模型算法，对于多模型算法的硬件实现却很少有人研究。作为多模型算法中最经典的算法，研究IMMEKF算法的硬件实现能够为其他多模型算法的硬件实现奠定基础。本文针对IMMEKF算法，将其转化为易于硬件实现的结构，并用Verilog HDL语言将其在FPGA上硬件实现。

1 纯方位角度跟踪问题

目标跟踪问题的本质是根据被噪声污染的观测数据来估计目标的状态[8]。假设目标在二维水平面上运动，则目标的运动状态可以用如下向量来表示

(1)

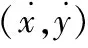
(2)

其中，Φ为状态转移矩阵，而Γ为系统噪声转移矩阵，H为观测方程状态转移矩阵，G为观测方程噪声转移矩阵，Wk-1和Vk均为均值为零的高斯白噪声，方差分别为Qk-1和Rk。观测方程是

(3)

观测值为k时刻目标与观测点连线和Y轴夹角的正切值。

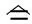
2 IMMEKF算法与仿真

2.1 IMMEKF算法

IMMEKF算法的每个模型都匹配扩展卡尔曼滤波器。计算流程可分为4个步骤：

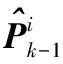
(4)

(5)

(6)

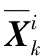
(7)

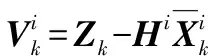
4)合成：将每个模型的估计结果合成

(8)

(9)

IMMEKF算法流程如图1所示。

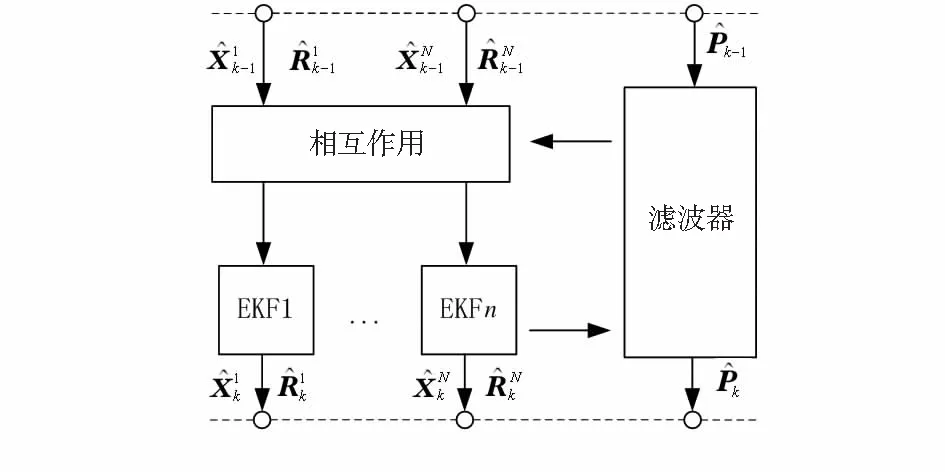
图1 IMMEKF算法流程图

2.2 仿真结果

表1 运动过程

从图2可以看出:估计轨迹与真实轨迹基本重合，算法较准确地跟踪了目标。从图3可以看到:在前1/3时间内，模型1(CV)的概率值分布在0.8～0.9之间，处于绝对优势地位;第二个1/3时间内，模型2(CT)的概率值分布在0.7～0.8之间;而在最后1/3时间内，模型1(CV)的概率值又分布在0.8～0.9之间。这说明算法能够较准确地对模型进行估计。而在模型转换时刻，概率值迅速发生跳变，这也保证了跟踪精度。

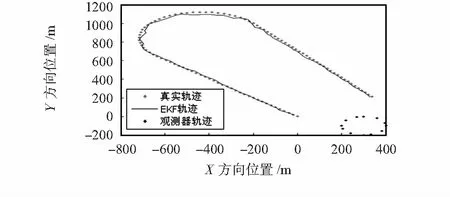
图2 IMMEKF算法跟踪效果图

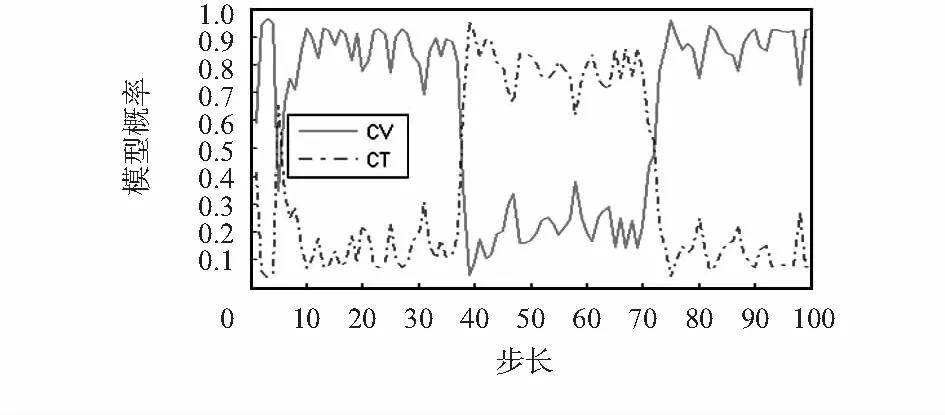
图3 IMMEKF算法各模型概率图

3 IMMEKF算法FPGA实现方案与仿真结果

本节介绍IMMEKF算法硬件实现的过程与在FPGA上进行硬件实现的方案和仿真结果,IMMEKF硬件算法模块框图如图4所示。

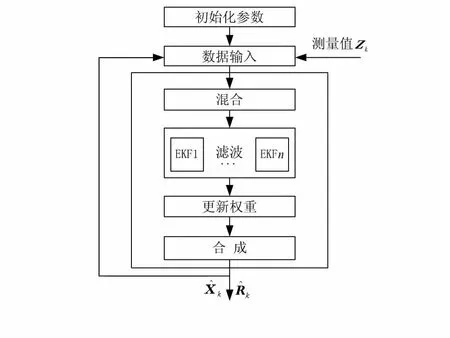
图4 IMMEKF硬件算法模块框图

算法所需的常量，如状态转移矩阵等，全部存储在FPGA的ROM中,当接收到新测量值Zk时，将所有数据输入滤波器进行处理。经过混合、滤波、更新权重、合成4个步骤后得到估计值k,然后等待下一次测量值的输入。

3.1 FPGA浮点数矩阵运算

IMMEKF算法需要用到大量的浮点数矩阵运算[9,10]。在FPGA上进行浮点数矩阵运算，如果采用芯片厂商提供的矩阵运算IP核，会消耗大量的硬件资源。所以,本文以芯片厂商提供的32位浮点数运算IP核为基础，编写了浮点数矩阵运算模块。计算4维向量内积和矩阵相乘的模块算法图见图5、图6。其中，图5为4维向量内积计算流程，图6为4维矩阵乘积计算流程。

图5 4维向量内积计算流程

图6 4维矩阵乘积计算流程

向量内积和矩阵乘积计算的第一步都是将向量或矩阵中的元素读取出来。对于向量内积计算，分别调用浮点数乘加模块进行计算,而对于矩阵乘积计算，则调用向量内积计算模块得到结果矩阵中的每一个元素。

3.2 仿真结果

在用Verilog HDL语言对上述硬件算法进行描述之后，对上文中所示纯方位角度跟踪问题，运用硬件算法进行跟踪。选择了Altera公司的Cyclone IV GX系列的FPGA芯片EP4CGX150DF31I7进行了综合和时序仿真，系统时钟设为50 MHz。

硬件仿真与软件仿真结果对比如图7、图8、图9所示。其中，图7表示软件仿真、硬件仿真跟踪结果，图8表示软、硬件仿真得到的跟踪结果之差，图9表示模型概率之间的差。

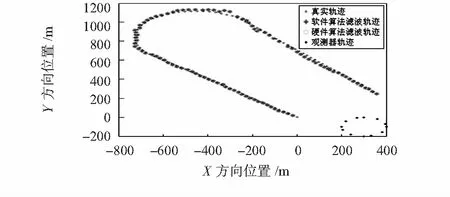
图7 软硬件仿真跟踪结果对比

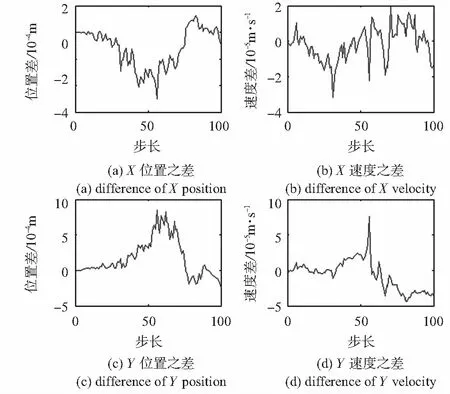
图8 软硬件仿真跟踪结果之差

图7表明：IMMEKF算法较准确地跟踪了目标，没有出现失跟，同时，软硬件算法得到的坐标估计值基本重合。这说明硬件算法的跟踪效果与软件算法相当。从图8可以看到,位置估计的误差在10-4数量级，而速度估计的误差在10-5数量级，而图9显示模型概率误差也在10-6数量级。

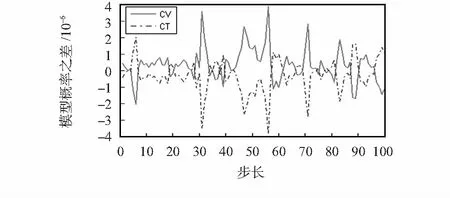
图9 软硬件仿真模型概率之差

软硬件算法跟踪误差绝对值最大值如表2所示。

表2 软硬件算法跟踪最大误差绝对值

这表明硬件算法能够达到与软件仿真相当的精度。在50 MHz脉冲激励下，每一步运算耗费时间530 898 876 ps。而同样的算法在Matlab环境运行时，每一步耗费时间约为0.01 s。可见，硬件算法能够实现对本文中机动目标的跟踪，而且相比软件仿真具有明显的速度优势，这在对运算速度有较高要求的军事场合是极为重要的。

4 结 论

本文针对纯方位角度跟踪问题，将IMMEKF算法分解成为适于硬件处理的结构，并给出了该算法在FPGA上硬件实现的方案。FPGA上的仿真实验表明：IMMEKF硬件算法能够对机动目标进行跟踪，并取得与软件仿真相当的精度，同时，运算时间大大减少。IMMEKF算法在FPGA上的硬件实现为该算法流片奠定了基础。

参考文献:

[1]权太范.目标跟踪新理论与技术[M].北京：国防工业出版社,2009.

[2]洪少华,史治国,陈抗生.用于纯方位跟踪的简化粒子滤波算法及其硬件实现[J].电子与信息学报,2009,31(1):96-100.

[3]Blom H,Bar-Shalom Y.The interacting multiple model algorithm for systems with Markovian switching coefficients[J].IEEE Transactions on Automatic Control,1988,33(3):780-783.

[4]Habtemariam B,Aravinthan A,Tharmarasa R,et al.Distributed tra-cking with a PHD filter using effcient measurement encoding[J].Journal of Advances in Information Fusion,2012,7(2):114-130.

[5]Georgescu R,Willett P,Marano S,et al.Predetection fusion in large sensor networks with unknown target locations[J].Journal of Advances in Information Fusion,2012,7(1):61-77.

[6]Yuan Ting,Bar-Shalom Y,Tian Xin. Heterogeneous track-to-track[J].Journal of Advances in Information Fusion,2011,6(2):131-149.

[7]Bolic M.Architectures for efficient implementation of particle filters[D].Stony Brook:Stony Brook University,2004.

[8]Arulampalam M,Ristic B,Gordon N,et al.Bearings-only tracking of maneuvering targets using particle filters[J].EURASIP Journal on Applied Signal Processing,2004(15):2351-2365.

[9]邬贵明.FPGA矩阵计算并行算法与结构[D].长沙:国防科学技术大学,2011.

[10] Dou Yong,Vassiliadis S,Kuzmanov G,et al.64-bit floating-point FPGA matrix multiplication[C]∥Proceedings of the 13th ACM/SIGDA International Symposium on Field Programmable Gate Arrays(FPGA’05)，Monterey:ACM,2005:86-95.