考虑高速非达西效应的油水相对渗透率计算模型

羊新州 ，汪浩 ，匡宗攀 ，李相方 ，吴克柳 ，朱彦杰

（1.中海石油深圳分公司，广东 广州 510000；2.中国石油技术开发公司，北京 100028；3.中国石油大学（北京）石油工程教育部重点实验室，北京 102249）

油水相对渗透率曲线的获取，对油藏开发方案的编制以及开发效果的预测具有重要的现实意义［1-7］。在高产油藏中，由于两相流体在储层中的高速流动，两相流体间的界面损耗加剧，产生两相高速非达西渗流现象，与常规油藏中的渗流特征不同［8-10］。常规相渗曲线都是在低速实验条件下得出的，可能会因为忽略生产过程中的惯性损失而导致油藏生产预测的误差，从页不能准确描述流体在高渗储层中高速流动时的渗流特征［11-14］。鉴于目前对于单相或者两相渗流流态认识的局限性，需要研究流体在多孔介质中高速流动的渗流规律，分析高速非达西效应对油藏生产的影响，为高孔高渗油藏产能的评价提供科学依据。

1 模型建立

模型假设：1）储层为均匀多孔介质；2）驱替方式为水驱；3）油水性质保持不变；4）油水不发生反应，并无相间传质现象；5）忽略储层及流体的压缩性质；6）忽略毛管力和重力；7）假设惯性系数β为常数。

1.1 运动方程

考虑高孔高渗储层多孔介质流体渗流特性，则油、水相非达西流运动方程可分别表达为

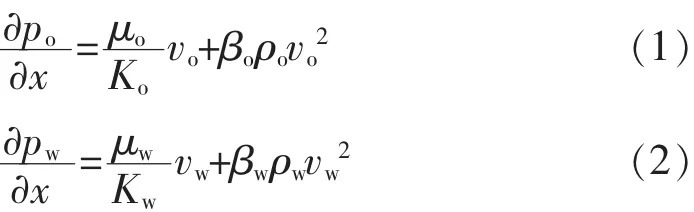
式中：p 为压力，MPa；x 为流动距离，m；μ 为黏度，Pa·s；K 为渗透率，10-3μm2；v 为渗流速度，m/s；ρ为密度，g/cm3；下标 o，w 分别代表油、水相。

油、水分流量表达式为

忽略毛细管作用力，则水相和油相压力梯度相等。由式（1）和式（2）得

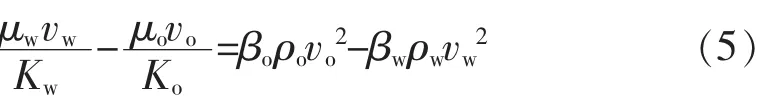
由于 fo+fw=1，将式（3）、式（4）代入式（5）并整理得

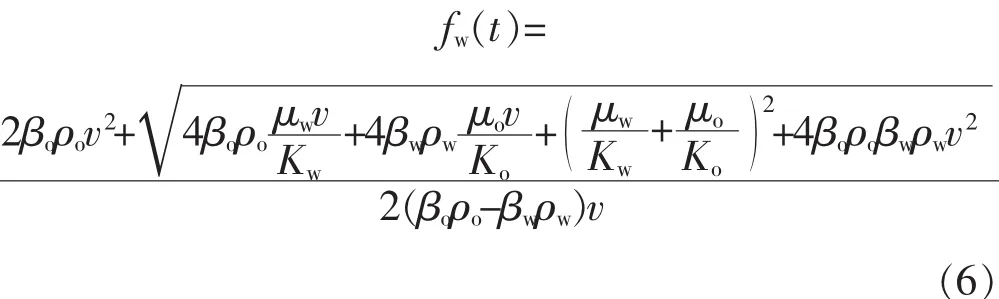
式中：t为流动时间，s。

1.2 Buckley-Leverett方程

根据渗流力学，忽略油水压缩性，则水相在一维均质地层中的连续性方程为

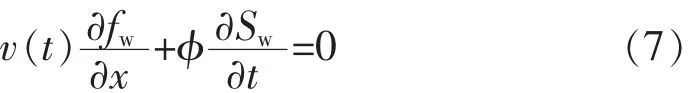
式中：φ为储层孔隙度；Sw为含水饱和度。

由式（7）可得到等含水饱和度面在多孔介质中的移动方程为

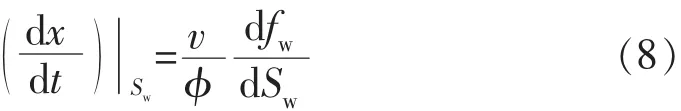
此即Buckley-Leverett方程，油水两相流体不可压缩时才适用此方程。其中含水率fw由式（6）代入，则式（8）即考虑了高速非达西效应的Buckley-Leverett方程。

1.3 油水相对渗透率计算模型

岩心两端压差与相对渗透率的关系，可在式（2）基础上变形后表达为

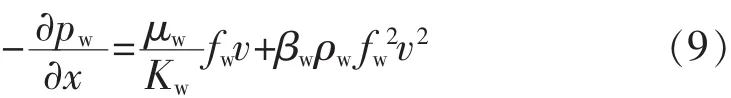
考虑到岩心为水湿岩心，故用水相的参数来表征岩心两端的压差：

式中：Δp为岩心两端压差，MPa；L为岩心长度，m。

依据等含水饱和度面推进速度，由式（7）可推导出

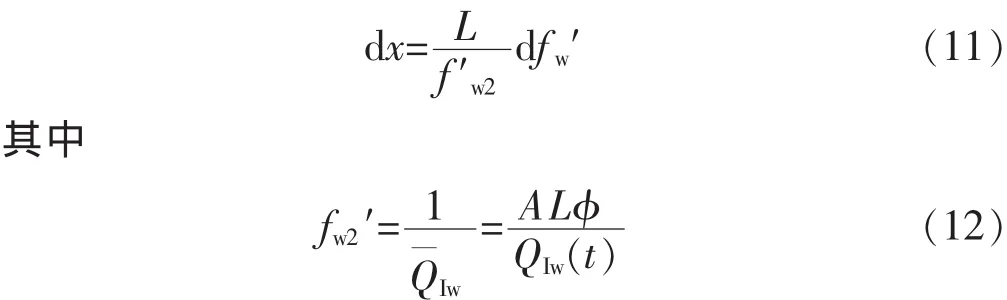
式中：fw2′为在岩心末端的分流量对含水饱和度的导数；fw′为分流量对含水饱和度的导数；为累积注入孔隙体积倍数；QIw（t）为累计注水量，m3；A 为岩心横截面积，m2。

将式（9）和式（11）代入式（10）得

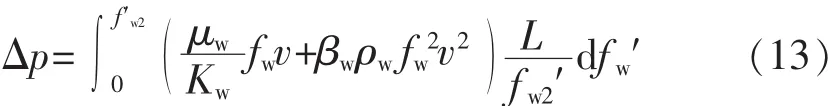
将式（12）代入式（13）并两端求导，整理得水相相对渗透率为

联立式（14）和式（6），油相相对渗透率可表达为

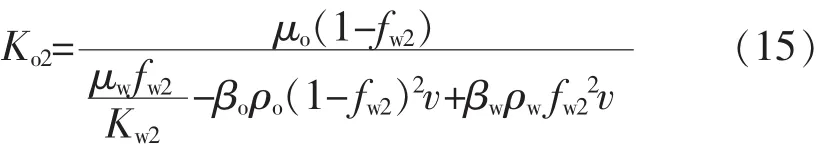
式中：下标“2”代表岩心末端处。

从水油两相相对渗透率式（14）和式（15）可知：1）如果不考虑油水两相高速非达西效应，式（14）和式（15）则为常规的JBN方法油水相对渗透率计算公式；2）油相非达西系数仅对油相相对渗透率有影响，对水相相对渗透率无作用；3）油水两相非达西系数均影响油相相对渗透率。

1.4 含水饱和度及梯度计算

由式（14）和（15）可知，计算油水相对渗透率首先必须先确定岩心末端的含水饱和度和水相分流量。

由物质平衡原理有：

式中：Swa为平均含水饱和度；Swc为束缚水饱和度；ΣQo为累计产油量，m3。

则岩心末端的含水饱和度表达式为

式中：Sw2为岩心末端处含水饱和度；fo2为岩心末端处油相分流量。

联立式（14），（15），（17），（19），就可得出高孔高渗储层多孔介质中油水渗流时，考虑高速非达西效应的油水相对渗透率曲线。

2 非稳态实验

2.1 实验样品

实验所用岩心数据见表1。原油密度为0.81 g/cm3，黏度为 9.15 mPa·s，体积系数为 1.047，原始气油比为7.24 m3/t。根据地层水矿化度配制实验用地层水，总矿化度为158 847 mg/L，pH值为5.64，水型为CaCl2型，密度为 1.01 g/cm3，地层温度下黏度为 0.6 mPa·s。

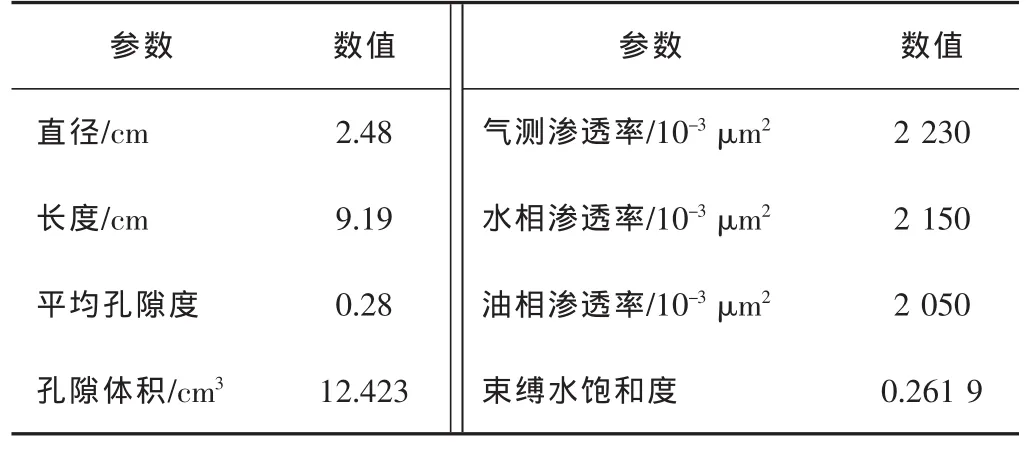
表1 岩心数据

2.2 实验装置及流程

本实验采用非稳态法水驱油实验测定油水相对渗透率曲线［15-17］。实验温度30℃，模拟原始地层条件下有效覆压40 MPa，驱替速度均为2.5 mL/min。

实验装置如图 1 所示，实验流程为［18-20］：1）对岩心进行清洗、烘干，测定岩心孔隙度；2）抽真空，饱和地层水，将饱和地层水的岩心装入岩心夹持器；3）调整好出口处的油、水体积计量装置；4）饱和油，建立束缚水饱和度，记录驱出的水量，计算岩心的含油饱和度和束缚水饱和度；5）在实验条件下进行水驱油，驱替至含水率达到或接近99%，并记录各个时刻的驱替压力、产油量、产水量。

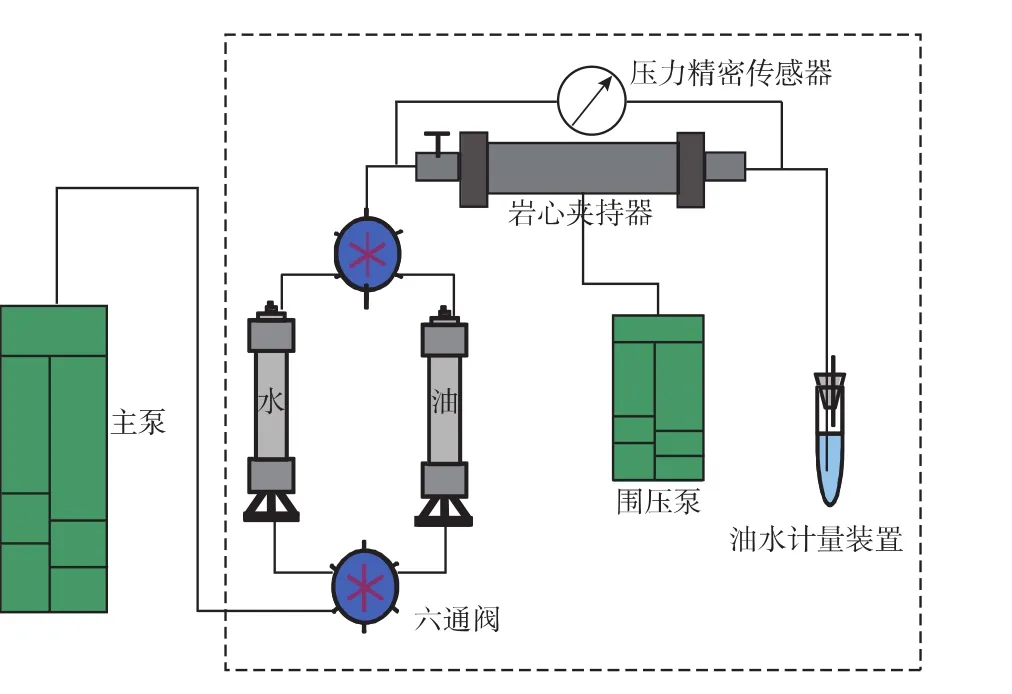
图1 ISCO 100DX多功能驱替装置

2.5 实验结果及分析

将实验结果代入式（14），（15）和（16），根据单相非达西渗流实验，确定水相非达西系数为1.6×106cm－1，油相非达西系数为1.6×106cm－1，可以得出油水两相渗流时考虑油相与水相高速非达西效应影响时的相渗曲线（见图 2）。

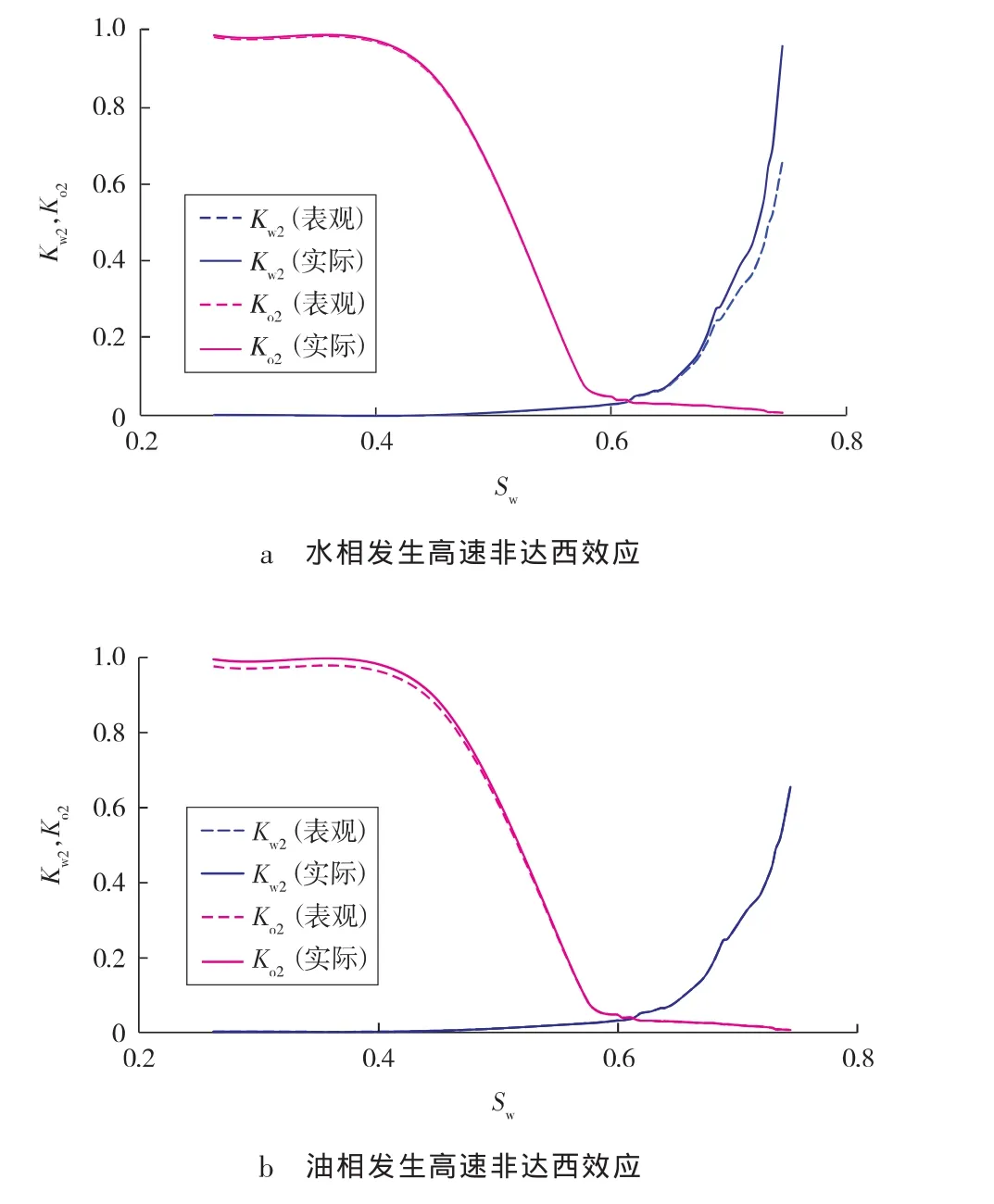
图2 油水相对渗透率曲线

由图2可知：1）油相发生高速非达西效应时，水相相对渗透率基本不变，油相相对渗透率下降；2）水相发

生高速非达西效应时，油相相对渗透率基本不变，水相相对渗透率下降幅度较大；3）产生油水两相高速非达西效应时，油水相对渗透率曲线均往下移动；4）两相高速非达西效应对相渗曲线的影响主要体现在水驱的初期和末期；5）发生两相高速非达西效应时，水相高速非达西效应对水相相对渗透率的影响更为明显。

3 油藏应用

3.1 数值模型的建立

根据西非某油田地层参数，建立了理论模型，数模所需的相渗曲线如图3所示。模型网格数为61×61×1，网格步长30 m×30 m×20 m，井距排距 900 m×900 m，孔隙度为20%，渗透率为2 000×10-3μm2，产油层平均深度为3 500 m，原始地层压力为40.0 MPa。模型采用反九点注采井网（见图4）。

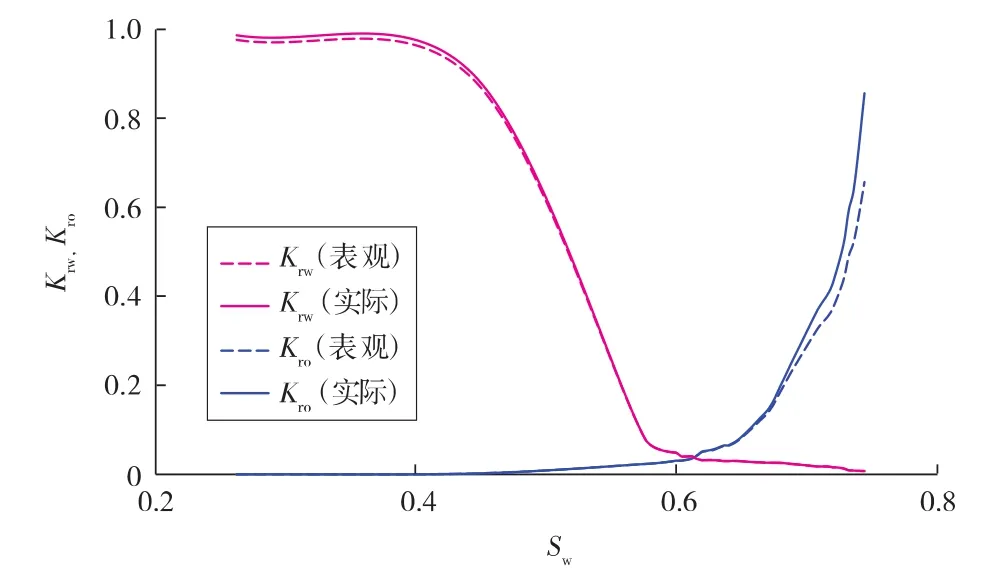
图3 考虑和不考虑高速非达西效应的油水两相相渗曲线

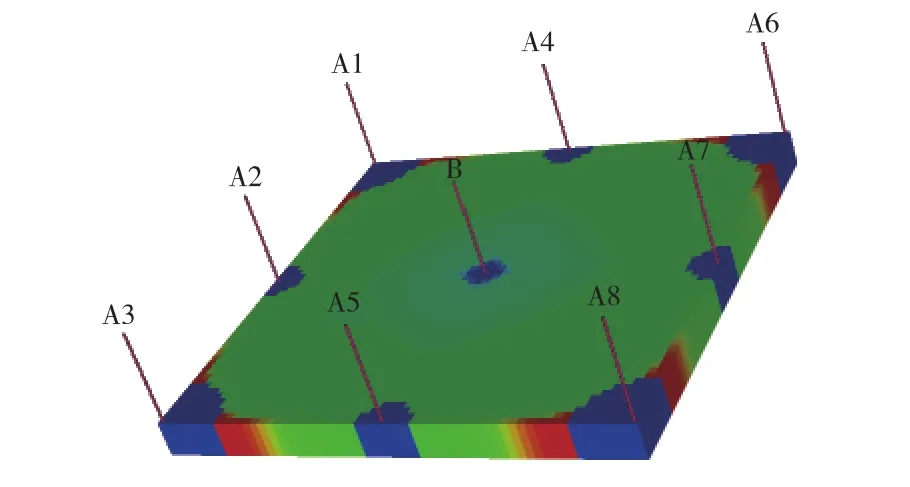
图4 井网模型

3.2 相渗对开发效果影响分析

分别进行2个方案模拟，方案一为考虑两相高速非达西效应，方案二为不考虑高速非达西效应，以定注定压方式进行模拟，模拟开发时间为10 a。2个方案在开发10 a后，生产指标如图5所示。

由图5a，5c可知，发生高速非达西效应的日产液量和日产水量均低于没有发生非达西效应时的日产量；由图5b可以看出，日产油量高于未发生高速非达西效应时的日产量。

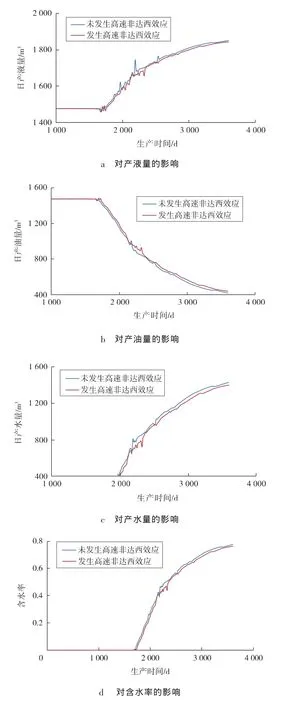
图5 两相高速非达西效应对开发效果的影响

该岩心的水相相对渗透率对高速非达西的敏感性要高于油相相对渗透率，当发生高速非达西效应时，流体在油藏中的渗流阻力增大，日产液量降低；生产后期，水相相对渗透率降低，而油相基本不变，油水流度比升高，油的流动能力增强，促进产油量增加。

由图5d可知，发生高速非达西效应时的含水率低于未发生高速非达西效应时。可见，油水两相高速非达西效应和单相高速非达西效应不同，并不一定都是阻碍油藏生产的负面因素，它可能会抑制水的产出，促进产油量的增加。

4 结论

1）建立并求解了高孔高渗油藏非稳态油水相渗计算数学模型。该模型考虑了高孔高渗储层中发生的高速非达西效应时对油水相渗的影响。

2）进行了非稳态油水相渗实验，并计算了考虑不同非达西系数对油水相对渗透率曲线的影响。实验及计算结果表明，水相非达西系数对油水相对渗透率曲线的影响较为明显，在含水饱和度低或者高的两端，非达西效应的影响较明显。

3）分析了高速非达西效应对高孔高渗油藏开发效果的影响。油藏数值模拟表明，油藏产水后高速非达西效应可以抑制水的产出，油藏产水以后，高速非达西效应虽然增加了流体的渗流阻力，但主要是降低水相的渗流能力，使油水流度比升高，抑制了油藏产水量，增加了油藏产油量。

［1］孙晓旭，杨胜来，李武广，等.疏松砂岩油藏冷冻岩心与常规岩心相渗曲线研究［J］.断块油气田，2012，19（4）：477-480.

［2］张继成，宋考平.相对渗透率特征曲线及其应用［J］.石油学报，2007，28（4）：108-111.

［3］章星，杨胜来，李芳芳，等.火山岩气藏气水两相渗流特征分析［J］.断块油气田，2013，20（5）：631-633.

［4］Jones S C，Roszelle W O.Graphical techniques for determining relative permeability from displacement experiments［J］.JPT，1978，30（5）：807-817.

［5］Sigmund P M，Mccaffery F G.An improved unsteady-state procedure for determining the relative permeability characteristics of heterogeneous porous media ［J］.SPEJ，1979，19（1）：593-608.

［6］桓冠仁，沈平平.一种非稳态油水相对渗透率曲线计算方法［J］.石油勘探与开发，1982，9（2）：52-58.

［7］杨小平.精确计算相对渗透率的方法［J］.石油勘探与开发，1998，25（6）：80-83.

［8］姚约东.石油非达西渗流新的运动模式理论及应用研究［J］.岩石力学与工程学报，2004，23（14）：177.

［9］Bennethum L S， Giorgi T.Generalized Forchheimer equation for two-phase flow based on hybrid mixture theory［J］.Transport in Porous Media，1997，26（3）：261-275.

［10］Barree R，Conway M.Multiphase non-Darcy flow in proppant packs［R］.SPE 109561，2007.

［11］Barree R D，Conway M W.Multiphase non-Darcy flow in proppant packs［J］.SPE Production&Operations，2009，24（2）：257-268.

［12］Wu Y S，Lai B，Miskimins J L，et al.Analysis of multiphase non-Darcy flow in porous media［J］.Transport in Porous Media，2011，88（2）：205-223.

［13］Lai B，Miskimins J.A new technique for accurately measuring twophase relative permeability under non-Darcy flow conditions［R］.SPE 134501，2010.

［14］窦宏恩.正确认识气藏高速非达西流湍流系数［J］.断块油气田，2013，20（4）：466-469.

［15］杨悦，李相方，吴克柳，等.考虑非达西渗流及毛管力的低渗油藏油水相对渗透率计算新方法［J］.科学技术与工程，2012，12（33）：49-54.

［16］易敏，郭平，孙良田.非稳态法水驱气相对渗透率曲线实验［J］.天然气工业，2007，27（10）：98-100.

［17］吕成远.油藏条件下油水相对渗透率实验研究［J］.石油勘探与开发，2003，30（4）：102-105.