声发射信号检测中谐振传导杆的设计与试验研究

毛汉颖，黄振峰，韦花貌，毛汉领

（1．广西科技大学 汽车系，广西 柳州 542506；2．广西大学 机械学院，南宁 530004）

对高温、深冷、易燃、易爆、有毒及核辐射或对复杂构件（设备）进行声发射检测时，由于条件限制或仪器设备使用的制约，不能将传感器直接安装在被测物体表面，而是通过不同的介质把被测物与传感器间接地连接起来，称为传导［1］。

研究人员对声发射传导方式进行大量研究，如李锦秀等［2］的专利研究地下岩体声发射信号聚焦传感，导波构件是用防锈金属制成的金属棒。王海斗等［3］的专利研究适于连接声发射探头的标准杆部件，可以精确地捕捉到声发射。蒋俊等［4］的专利研究了一种用于声发射检测的传导杆及两个连接端。王祥岗［5］研究了三种高低温容器检测时常用的传导杆，便于在狭小的空间安装。邹银辉［6］运用一维黏弹性波理论推导出了声发射简谐波在传导杆传播过程中位移、速度及加速度幅值绝对值与传播距离成指数衰减关系。邹银辉等［7］还对于同一类型传导杆进行试验研究，发现传导杆长度不同对信号的振幅的变化率和事件计数都有影响。李建功等［8］得出了传导杆的直径越小，固定端加速度幅值的绝对值越大，从固定端点到自由端点加速度幅值的绝对值衰减率也越大的结论。孙国豪等［9］指出对于同一直径的传导杆，声发射信号的幅值随着传导杆长度的增长而降低；对长度相同的传导杆，声发射信号的幅值随着传导杆直径的增大而幅值降低。郭福平等［10］发现传导杆上传感器接收到的信号波形相似，振幅存在衰减，但频率分布基本相同。吕毛三等［11］用弹性动力学理论设计杆底部为阶梯形或圆锥形接头的新型导波杆，与普通导波杆相比，其可以起到放大声发射信号作用，最大放大倍数不到2。虽然一些研究探讨了传导杆对声发射信号的影响，但仍没有找到解决传导杆导波会使声发射信号会再次衰减的问题。

为此，我们首次提出基于共振理论的声发射检测谐振传导杆的设计方法，由此设计研制了不同材料、不同谐振长度的传导杆，断铅模拟声发射试验表明，谐振传导杆对声发射信号具有幅值放大和带通滤波功能，其效果与传导杆的材料和结构尺寸有关。研究结果为在复杂结构中检测弱小的声发射信号提供了一种全新的技术基础。

1 谐振传导杆的设计方法

传导杆功能就是传导和放大信号，谐振传导杆就是借助被检测声发射信号激励达到共振，使输出端质点位移（速度）的振幅比输入端质点位移（速度）的振幅大很多，达到放大信号的目的。

谐振传导杆的设计要求是，在谐振频率下产生共振现象，使输入端信号传导至输出端后幅值放大。

1．1 谐振传导杆的设计理论

为满足谐振设计要求，一般选用变截面杆，阶梯形状是变截面最简单的形式，如图1所示，选择阶梯形杆来进行谐振传导杆的设计。设定阶梯形变截面处为x＝0，作用在传导杆的输入端与输出端的力与振动速度分别是F11与F2，，这样阶梯形的传导杆在谐振运动状态下的纵向振动方程为：

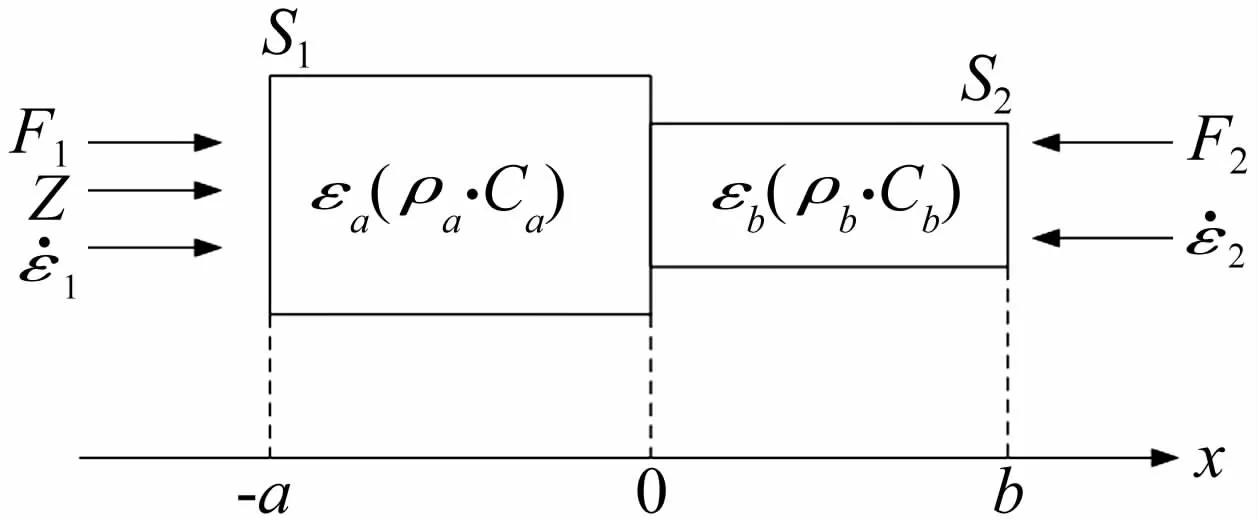
图1 阶梯形的传导杆Fig．1 Stair amplitude transformer

由边界条件，解微分方程可得到谐振的阶梯形传导杆的得放大系数为

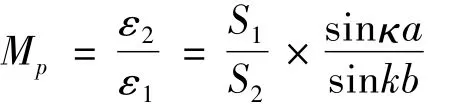
特别是，当a＝b时，放大系数为

当a＝2b时，放大系数为

式中分别为传导杆输入端、输出端的半径。

由于传导杆是用同一种材料做成的，并且希望有一定的放大倍数，即S1≠S2。

（1）当a＝b＝l／2时，谐振的频率公式可以写成因此谐振长度的方程为 kl／2

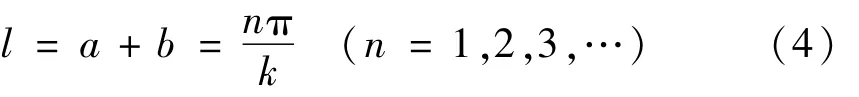
（2）当a≠b时，谐振的频率公式可以写成

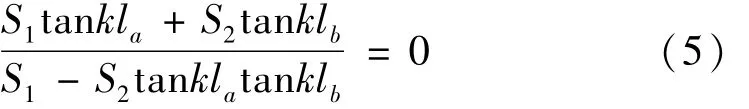
设计成谐振状态，是为了放大声发射信号，因此在实际设计过程中，N的范围一般在1．01到10之间，阶梯形传导杆的放大倍数理论上在1．01到100之间。

1．2 谐振传导杆的设计

声发射信号是高频宽带信号，一般金属断裂的中心频率约为120 kHz、HB铅笔折断的中心频率是80 kHz、木材折断的中心频率是8 kHz。为了使所设计的谐振传导杆，能对宽带的声发射信号有较好的放大效果，可以选择声发射信号的中心频率为谐振传导杆的设计频率。经过谐振传导杆后，不但会对信号幅值有放大作用，而且还有带通滤波作用。

本文是采用HB铅笔折断的声发射信号进行试验的，所以选择传导杆谐振固有频率为f0＝80 kHz，为传导杆的理论固有频率。

设阶梯形的传导杆大端直径为D，理论谐振长度为L，则比值为α＝D／L，得实际的谐振长度li与理论长度L的关系：

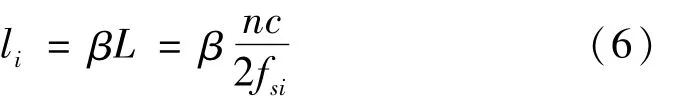
式中：n表示位移节点的数量为频率降低系数，fsi为阶梯形传导杆工作时的实际频率，c为纵波在传导杆中传播速度。为便于加工，选择 α大一些，如取α＝45，N＝3，由文献［12］查得 β＝0．91。

1．2．1 不同材料的传导杆设计计算

当a＝b、N＝3时，理论放大系数 Mp＝9，对钢、铝和黄铜等不同材料设计的0．5倍波长阶梯传导杆。由文献［12］查得，纵波在45＃钢中传播速度 c1＝5．2×106mm／s、在铝中传播速度 c2＝6．4×106mm／s、在铜中传播速度c3＝3．8×106mm／s，设计计算结果如表1所示。

1．2．2 横截面积比相同的不同谐振长度的传导杆设计计算

当a＝b、N＝3时，理论放大系数 Mp＝9，以黄铜材料设计不同谐振长度的阶梯形传导杆，结果如表2。

1．2．3 横截面积比不同的2倍波长的黄铜材料传导杆设计计算

当 a＝b时，取 α＝0．45，分别使 N＝2，N＝4，设计得到节2倍波长（节点数为4）黄铜材料阶梯形传导杆如表3。

1．2．4 横截面积比相同的两端长度不相等的黄铜传导杆设计计算

当 la＝2lb、N＝3时，代入式（4）、（3），得出谐振长度的方程为 klb＝Mπ，其中 M为1，2，3，…，理论放大倍数都为同样以黄铜材料设计出三个阶梯形传导杆如表4。部分加工出来的实物如图2。

图2 不同谐振长度的黄铜阶梯形传导杆Fig．2 The object pictures of the different resonance length of stepped ultrasonic horn

表1 钢、铝和黄铜等不同材料的半波长阶梯形传导杆设计尺寸Tab．1 Different materials of half-wavelength stepped horn

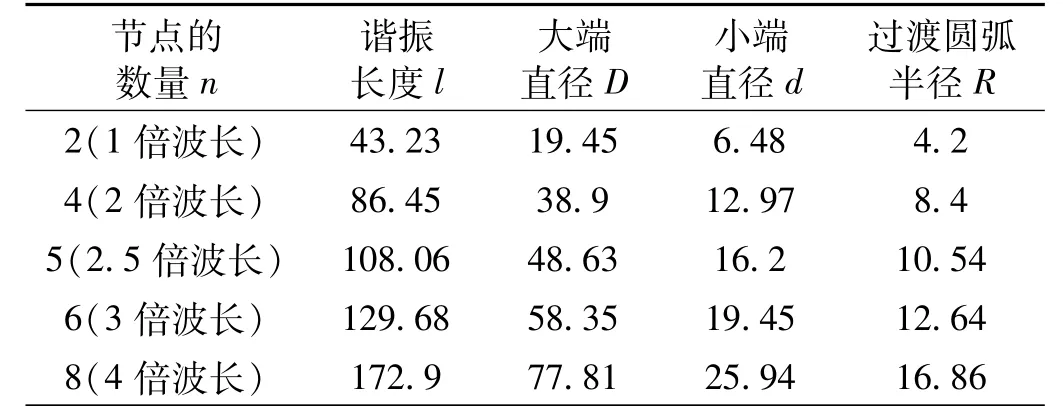
表2 不同谐振长度的黄铜材料的阶梯形传导杆Tab．2 The same materials and different resonance length of stepped horn

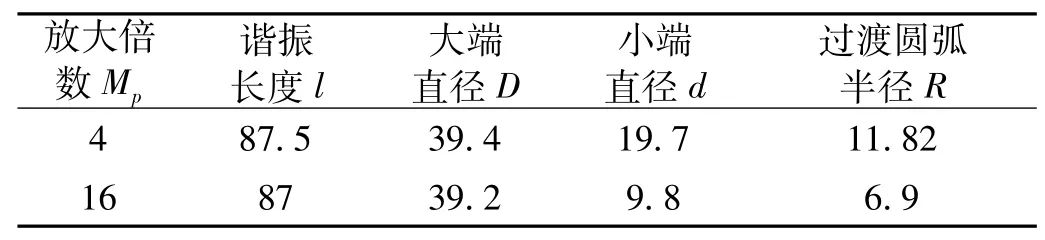
表3 理论放大倍数不同的2倍波长黄铜阶梯形传导杆Tab．3 Both different number nodes and theory amplification factor of stepped horn

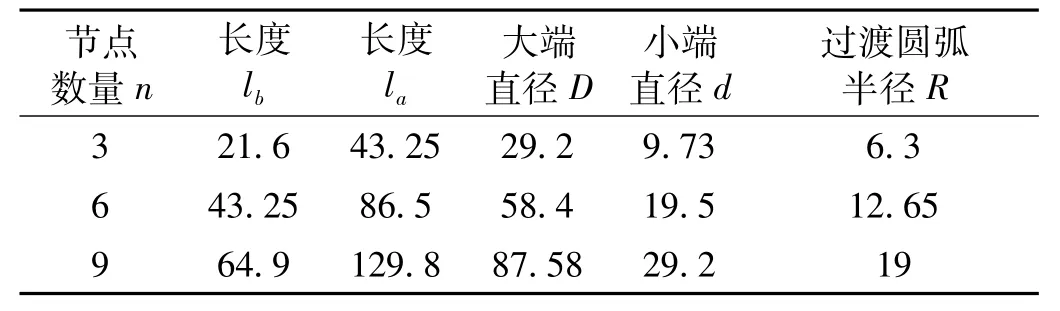
表4 理论放大倍数相同的不同谐振长度的黄铜阶梯形传导杆Tab．4 The same theory amplification factor and different resonance length of stepped horn

2 谐振传导杆试验研究

2．1 试验目的和条件

试验设计目的就是研究声发射信号经过谐振传导杆后是否有放大作用和滤波效果。主要用几种常见的材料来设计谐振传导杆，选择放大效果最好的材料作为后面设计所用材料；不同的谐振长度试验研究，选择放大和滤波效果最好的谐振长度；谐振长度相同，横截面积比例不同变幅杆的试验研究等；通过改变长度与直径设计出不同的传导杆，分析谐振传导杆的材料、谐振长度与横截面积对放大倍数与滤波效果的影响。

断铅模拟声发射信号采集试验如图3所示，试验条件主要包括：① 45号钢板，尺寸为长820 mm×宽495 mm×厚5 mm，用软垫支承；② 声发射源，以直径0．7 mm、伸长量2．5 mm的2B铅笔芯与钢板表面成30°角折断铅笔芯模拟声发射信号；③ 谐振传导杆，按上述设计研制的谐振传导杆，谐振频率为80 kHz；④两个声发射传感器，传感器型号为SR150M，频率范围50～400 kHz，谐振频率为150 kHz；⑤ PAV型前置放大器，选择带宽为100～400 kHz，增益为40 dB；⑥ 成都中科动态信号采集卡，包括一块PCI4712四通道的采集卡，每个通道A／D分辨率为12 bit，采样频率范围为1 kHz～50 MHz；⑦ 软件分析系统，采集卡配套的分析软件是DasView2．11，通过这个软件分析系统可以获得声发射信号波形和声发射的特征参数值等；⑧ 耦合剂：凡士林和AB胶，传导杆的大端用AB胶黏固在钢板上，传感器用凡士林与钢板或传导杆小端耦合。

由于没有标准的声发射传感器，而且后面需要同时使用两个传感器，故标定时任选其中一个传感器作为标准。将标准传感器记为传感器1，另一个传感器记为传感器2。标定过程如下：① 把两个传感器安装在钢板上，在它们的耦合界面用凡士林耦合，且他们的中心距为120 mm，在它们的中心点O处断铅并采集断铅声发射信号，然后对采集到的声发射信号进行处理；②考虑到距离对信号的影响，两传感器的位置不动，分别在A，B，C，D（这些点在两传感器的中垂线上且两点间的距离为20 mm，如图3。）点断铅5次并采集信号，然后用传感器2信号的峰峰值比上传感器1信号的峰峰值。为消除钢板材质可能不均匀影响，将两个传感器的位置对换一下，再做一次断铅试验，然后对声发射信号进行处理。标定试验表明，传感器2的峰峰值大概是传感器1的0．98倍左右，两个传感器误差在2%以内，被测传感器2的输出振幅比标准传感器1的输出振幅的相对灵敏度误差也在2%范围内，从信号时序图和频谱图分析发现两个通道的信号非常接近，因此可以使用这两个传感器采集信号进行对比试验。

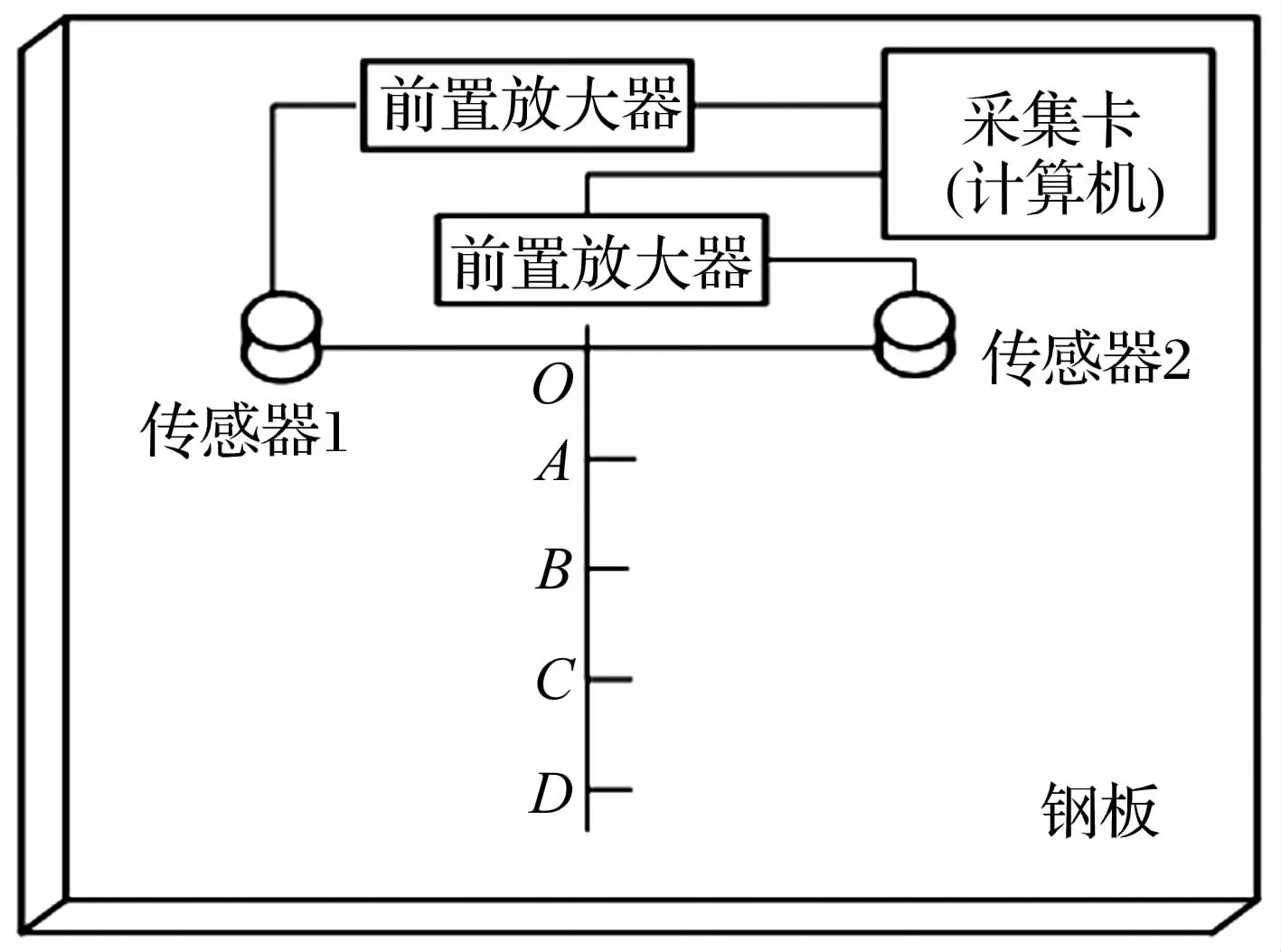
图3 模拟断铅声发射信号采集试图Fig．3 The acquisition process figure of transducer calibration

2．2 谐振传导杆试验研究

2．2．1 试验过程

（1）在标定后，传感器2的位置不变，分别将几种谐振传导杆安放在传感器1的位置，传导杆大端面与钢板的耦合界面用AB胶黏连，传感器1安装在传导杆上面且中心对齐，传导小端面与传感器1的耦合界面使用凡士林耦合。

（2）在变幅杆与传感器2连线的中垂线上O、A、B、C、D（这些点在两传感器的中垂线上且两点间的距离为20 mm）等5个点上，利用0．7 mm 2B铅笔芯分别在5个进行断铅试验，模拟在5个点的声发射源，Das-View2．11控制软件采用上升沿触发自动采集断铅声发射信号。

（3）更换不同的谐振传导杆重复步骤（1）、（2），记录传感器1和传感器2的信号，直到完成这四组实验。为了试验结果的准确性，在更换谐振传导杆时再次对传感器进行标定。

放大倍数：断铅声发射信号经过谐振传导杆后在传感器1所检测到信号的最大峰峰值与传感器2上所检测到的直接传播原信号的最大峰峰值之比，每次试验都分别求出信号的放大倍数，并分别计算出四种谐振传导杆的放大倍数均值。

滤波带宽：传导杆的谐振频率为 f（选定为80 kHz），在这个频率下经传导杆的信号幅值应该达到最大，当幅值下降3 dB时，即下降到最大值的0．707倍，所对应的两个频率为f1、f2为谐振传导杆对信号的滤波带宽的截止频率，滤波带宽为：Δf＝f2－f1。四种谐振传导杆的试验数据处理结果如表5～8。

2．2．2 试验结果分析

试验结果表明，断铅声发射信号经过45＃钢、铝和黄铜材料的半波长阶梯形谐振传导杆后（理论放大倍数相同），峰峰值的放大比M黄铜＞M45＃＞M铝，材料的密度越大，信号放大倍数也越大。由于加工误差和耦合界面的反射，或者波在材料中的传播速度与理论值有一定的差距，导致设计出来传导杆的实际振动频率与理论振动频率有一定的偏差，因此放大倍数没有达到理想的状态。对信号滤波带宽进行分析，发现黄铜材料的带宽最大，45＃钢材料带宽次之，而铝材料带宽最小，材料的密度越大，信号的滤波带宽越宽。

试验结果表明，断铅声发射信号经过不同谐振长度的传导杆后放大倍数均值有结果M2＞M4＞M1＞M5＞M25，下标分别表示波长的倍数，可以认为2倍波长的传导杆放大倍数最大而且比较均匀。断铅信号经过传导杆后在低频或者高频段信号都非常微小，而在共振频率80 kHz左右信号的振幅很大，声发射信号经过不同谐振长度传导杆后有滤波效果，经过1倍波长、2倍波长、2．5倍波长、3倍波长和4倍波长的传导杆后，得到信号的滤波带宽分别为 8．85 kHz、8．66 kHz、8．75 kHz、8．16 kHz和 8．72 kHz。滤波带宽变化不大，没有与谐振长度有关的明显规律。

试验结果表明，断铅声发射信号经过谐振长度相同、横截面积比不同的传导杆后放大倍数有较大变化。信号经过横截面积比N值为2的变幅杆，理论放大倍数为4但经过试验得到的信号放大倍数比4小一些，信号经过横截面积比N值为4的变幅杆，理论放大倍数为16，但经过试验得到的信号放大倍数比16小一些，横截面积比N的值越大，则信号的放大倍数也越大。信号经过横截面积比N值为2的传导杆，信号的滤波带宽为8．98 kHz；经过横截面积比N值为4的传导杆，信号的带宽为8．55 kHz。材料和谐振长度相同横截面积比不同的变幅杆，横截面积比N为4信号放大比最大，横截面积比N为3次之，横截面积比N为2的信号放大比最小，可得出横截面积比越大则放大倍数也越大。因为加工存在误差合耦合界面的反射，所以放大比与理论值有一定的差距。信号的滤波带宽，横截面积比N为4最小，横截面积比N为3次之，横截面积比N为2最大，信号滤波带宽随着横截面积比的增大而减小，但变化也不大。

试验结果表明，断铅声发射信号经过理论放大倍数相同的不同谐振长度的黄铜阶梯形传导杆放大倍数如表9，横截面积比相同，但大端长度是小端长度2倍时，理论放大倍数增加为2倍，实际放大倍数也接近增加为2倍，接近18。

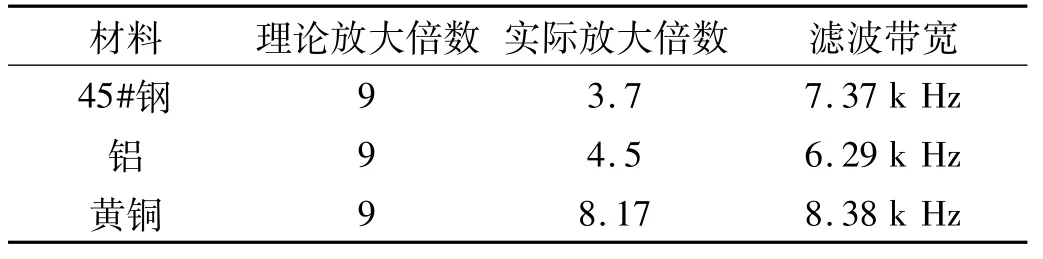
表5 钢、铝和黄铜等不同材料的半波长阶梯形传导杆的试验结果Tab．5 Experiment results for different materials of half-wavelength stepped horn

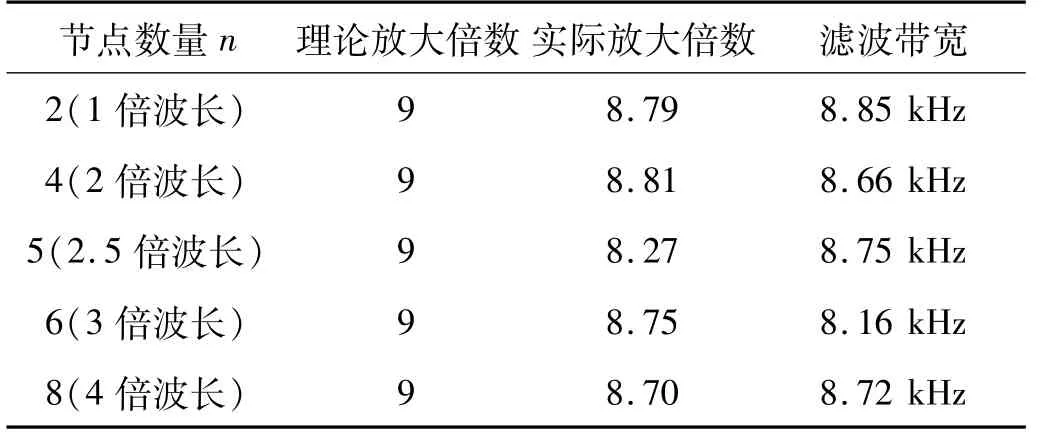
表6 不同谐振长度的黄铜材料的阶梯形传导杆的试验结果Tab．6 Experiment results for the same materials and different resonance length of stepped horn

表7 理论放大倍数不同的2倍波长黄铜阶梯形传导杆试验结果Tab．7 Experiment results for 2 wavelength stepped horn

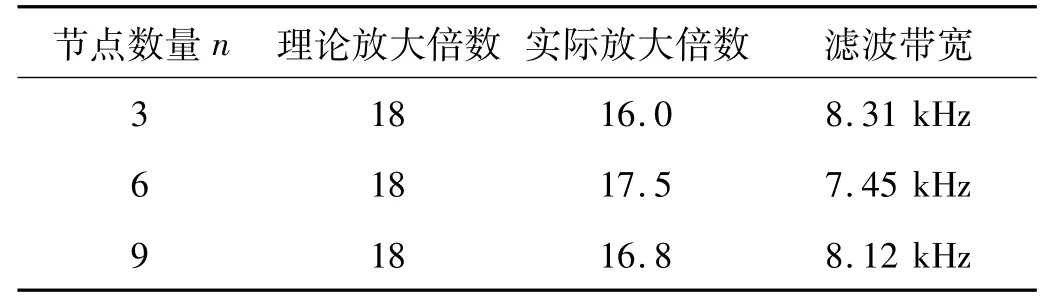
表8 理论放大倍数相同的不同谐振长度的黄铜阶梯形传导杆Tab．8 Experiment results for the same theory amplification and different resonance length of stepped horn

3 结 论

从理论和试验两方面论证了利用谐振原理设计传导杆的可行性，所设计研制的谐振传导杆可实现声发射信号振幅放大、声发射信号经过谐振传导杆后有带通滤波作用，得到以下结论：

（1）信号放大倍数受到谐振传导杆的材料密度、横截面积比、谐振长度（输入相位与输出相位）等这些因素的影响。材料密度越大，信号的放大倍数也越大。横截面积比越大，信号的放大倍数也越大。

（2）对声发射信号的滤波带宽受到材料密度、横截面积比、谐振长度和声发射源的距离等因素影响，但信号滤波带宽总体变化不大。

（3）可以针对不同的应用要求，采用不同的中心频率来设计谐振传导杆，实现对结构的声发射监测，在实际应用中发挥作用。

［1］杨明纬．声发射检测［M］．北京：机械工业出版社，2005：1－50．

［2］李锦秀，刘志刚，谭云亮，等．一种地下岩体声发射信号聚焦传感装置［P］．中国国家知识产权局：201120152206．8，2011．11．30．

［3］王海斗，杨大祥，张玉波，等，适于连接声发射探头的标准杆部件［P］．中国国家知识产权局：201120184125．6，2011．12．07．

［4］蒋俊，梁华．一种用于声发射检测的波导杆［P］．中国国家知识产权局：200910234666．2，2010．06．09．

［5］王祥岗．高低温容器声发射检测中几种声波传导方法［J］．故障诊断，2011，14（5）：46－48．WANG Xiang-gang．Several conduct ways for the acoustic emission detection［J］．Diagnosis，2011，14（5）：46－48．

［6］邹银辉．声发射系统中的一维黏弹性波导器理论模型［J］．煤炭学报，2007，32（8）：799－803．ZOU Ying-hui．The theory model for the acoustic emission system［J］．Journal of Coal，2007，32（8）：799－803．

［7］邹银辉，董国伟，张庆华，等．波导器中声发射信号传播规律研究［J］．矿业安全与环保，2007，34（6）：13－17．ZOU Ying-hui，DONG Guo-wei，ZHANG Qing-hua，The research on the acoustic emission transmission in the conductors［J］．Safe and Environment Protection for Mining，2007，34（6）：13－17．

［8］李建功，邹银辉．AE声发射在波导器中传播规律的数值模拟［J］．地下空间与工程学报，2008，4（6）：1148－1151．LI Jian-gong， ZOU Ying-hui． The simulation for AE transmission in the conductors［J］．Journal of Undergounf and Engineering，2008，4（6）：1148－1151．

［9］孙国豪，柏明清，张春江，等．圆形波导杆中两种情况下声信号的传播特性［J］．华东理工大学学报，2010，36（6）：851－858．SUN Guo-hao，BAO Ming-qing，ZHANG Chun-jiang，et al．The transmission characteristics of the round conductors［J］．Journal of Huadong University in Technology，2010，36（6）：851－858．

［10］郭福平，李伟．波导杆辅助声发射检测承压管道泄漏实验研究［J］．化工机械，2009，36（4）：287－290．GUO Fu-ping，LI Wei．The experimental research on the acoustic emission detection with the conductors［J］．Chemical Machinery，2009，36（4）：287－290．

［11］吕毛三，黄振峰，毛汉领．声发射信号在导波杆中传播的放大规律实验研究［J］．现代电子技术，2010，11（3）：167－170．LU Mao-san， HUANG Zhen-feng， MAO Han-ling． The experimental research on the amplifier for the conductors［J］．Modern Electronic Technique，2010，11（3）：167－170．

［12］林仲茂．超声变幅杆的原理和设计［M］．北京：科学出版社，1987：178－186．