EMD 包络谱在虚拟仪器诊断系统中的实现及应用
李贵子,楼军伟
(1.甘肃省机械产品检测与技术评价重点实验室,甘肃兰州730302;2.兰州理工大学机电工程学院,甘肃 兰州730050)
0 引言
N.E.Huang[1]等人在1998年提出的经验模态分解能对信号进行多尺度分解为多个内禀模态函数(intrinsic mode function,简称IMF),与小波变换相比,无须预先设定任何基函数,是一种自适应的方法,非常适合于非平稳、非线性信号的分析,已广泛应用于齿轮[2]、轴承[3]等的故障诊断中。Labview是一个功能强大而又灵活方便的虚拟仪器开发工具,在界面开发和信号采集方面有强大的功能,但是在信号处理算法支持方面非常有限。而Matlab在信号和图像处理等领域具有无可比拟的优势,几乎对所有的工程计算都提供支持,但其人机交互界面和信号采集能力较差。为此,将Labview和Matlab二者优势互补,利用Matlab Script节点技术混合编程[4]在虚拟仪器诊断系统中实现EMD包络解调分析。实例应用结果表明Labview开发的主界面具有良好的人机交互和图形化显示界面,Matlab提供的EMD包络解调在处理非线性、非平稳轴承信号时能准确识别故障特征频率,三者的有机结合在工程中具有广阔的应用前景。
1 Matlab Script节点技术介绍
Labview程序框图中单击鼠标右键,选择数学/脚本与公式/脚本节点/Matlab脚本,创建 Matlab Script节点。Matlab Script节点技术的实质是将 Matlab当作一个ActiveX服务器,并建立ActiveX通道,运行时Labview将函数或命令通过ActiveX通道发送给Matlab,由Matlab在后台执行,执行完后在Labview前面板显示,显示时可选择Matlab直接图形显示,也可添加输出用Labview波形显示控件显示,文中前者显示方法。图1为Matlab Script节点技术信号传递处理示意图。用该方法进行混合编程既简单又实用,但有以下几点必须注意[5]:

图1 Matlab Script节点技术信号传递示意图
1)只能用于Windows平台的计算机,必须同时安装有Labview和Matlab软件;
2)Matlab Script节点技术因为执行脚本节点时要调用Matlab脚本服务器,只有 Matlab 5.0及以上版本才支持;
3)Labview和Matlab是两种不同的编程语言,有各自的数据类型,所以在应用时必须注意Matlab脚本节点输入输出数据类型的匹配,否则Labview运行时将产生错误。数据类型匹配可以从输入输出端快捷菜单上的数据类型中选择。
2 EMD包络谱算法
经验模态分解被认为是以傅里叶变换为基础的线性、稳态信号分析的一个重大突破[6]。基于如下假设:信号不论是线性或是非线性的、非平稳的,都具有相同数量的极值点和过零点,或最多相差一个;由所有极大值极小值点确定的上下包络线关于时间轴局部对称,即均值为零。EMD对非线性、非平稳信号按时间序列分解得到能满足上述假设的IMF分量。对信号x(t)的具体分解步骤如下:
1)用三次样条曲线连接信号x(t)所有局部极大值点和所有局部极小值点得到上下包络线,求上下包络线平均值记为m1(t),令:
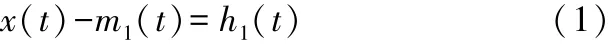
如果h1(t)是满足IMF分量要求,则循环停止。
2)若不满足,则返回以h1(t)为原始信号按第(1)步继续求上下包络线以及平均值m2(t),令:

判断h2(t)是否满足IMF分量要求,如此循环n次,直到:

式中:hn(t)满足IMF分量要求为止。
3)此时,将hn(t)分离出来,记c1(t)=hn(t)为信号x(t)的第一层IMF分量,得到:

4)判断r1(t)是否单调,若不是,再重复以上步骤n次,得到信号x(t)所有层次的IMF分量为止。
即:

5)那么原始信号x(t)组成如下:

式中:rn(t)—残余函数,代表信号平均趋势。
6)对分解得到的每一层IMF分量 ci(t)做Hilbert变换得到:
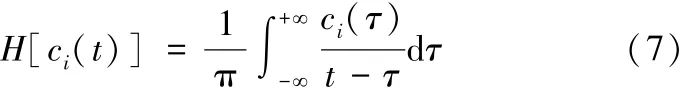
7)构造解析函数wi(t)
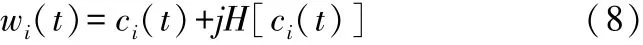
8)求每一层IMF分量ci(t)的包络谱

3 EMD包络谱的实现
打开Labview2010,按数学/脚本与公式/脚本节点/Matlab脚本创建Matlab Script节点。可以直接输入程序也可以在脚本节点上单击鼠标右键“导入”。文中采用后者,即预先在Matlab 7.0中编写、调试好程序,再导入脚本节点,程序是按子程序方式编写,因此需在诊断系统目录下存放 emd.m,hua_baol.m,hua_fft.m 等 Matlab M 文件,实际应用中按照不同的信号选择不同的EMD分解层数,图2所示的程序修改方便。Labview与Matlab Script节点之间数据的交换通过右键单击节点框左或右边框,选择“添加输入”或“添加输出”来实现,这样数据就可以从Labview传递给Matlab进行分析和处理,完成的结果返回给Labview显示,需要注意的是数据类型的匹配。图2中添加了输入信号“A”,该信号是以调用子Vi的方式从现场测得的并保存在Access数据库中的数据读取,数据类型是一维数组。此外还添加了采样频率输入端“B”,采样点数输入端“C”,为了便于分频查看,还添加了频率起点和终点输入端“E”和“F”,数据类型均为实数。

图2 系统Labview后面板
图3是EMD包络谱系统Labview的前面板,前面板中给出了操作步骤说明,在第二步中是所需要输入的EMD包络谱参数,即后面板中的采样频率输入端“B”,采样点数输入端“C”,频率起点和终点输入端“E”和“F”。结果显示是以Matlab作图方式直接在Labview中显示的,还可以查看处理后的数据等。整个前面板具有良好的人机交互和图形显示界面。
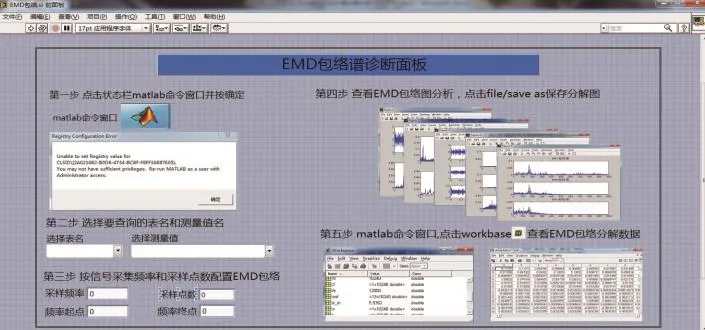
图3 系统Labview前面板
4 实例应用
滚动轴承的损伤有表面损伤和磨损两种,其振动信号是典型的非平稳、非线性信号。由于磨损是一种渐变性损伤,没有具体数学模型确定故障频率,因此文章只针对表面损伤。发生表面损伤的轴承在运转过程中损伤点撞击与之相接触的其他元件表面而产生低频振动频率称为故障特征频率,由轴的转速、轴承几何尺寸及损伤的位置确定。具体为:
轴承外圈损伤特征频率:

轴承内圈损伤特征频率:

轴承滚动体损伤特征频率:

轴承保持架损伤特征频率:

式中:z—轴承滚动体数;fr—电动机转速;d—轴承滚动体直径;D—轴承节径;α—接触角。
实例中选取电机驱动端轴承,型号为6205,采样频率为12 kHz,采样点数为10 240,人为破坏的点蚀损伤直径为0.2 mm,深度为0.2 mm。在电动机负载为1.45 Kw,转速为1 750 r/min时采集正常和内圈点蚀的振动信号,并存入Access数据库。
经式(10)可知电动机转频为29.12 Hz,内圈故障特征频率157.7 Hz。由于测取的信号存在噪声污染,为了防止噪声导致多次EMD分解带来端点效应累积误差[7]预先进行3层db4小波降噪和重构,然后对正常和内、外圈振动信号进行EMD包络谱分析,输入和信号采集时一样的采样频率、采样点数,选取0-1 000 Hz。
图4、图5分别轴承正常和点蚀损伤时是EMD包络谱分析的结果,通过比较可知:
1)损伤时的信号较正常时的信号更为复杂,若直接对损伤时的原始信号进行快速傅里叶频谱分析无法有效分辨出故障特征频率。
2)轴承正常时从图4(c)可知第1层IMF分量包络谱中有29.3 Hz,第2层IMF分量包络谱有29.3 Hz以及其2倍频,均非常接近电动机轴转频29.12 Hz。此外在第2、3层信号峰值递减高频处无突变峰值,趋于平稳。
3)轴承损伤时从图5(c)可知各层均存在电动机轴转频29.3 Hz以及其2倍频和内圈故障特征频率157.5 Hz且峰值较高。特别是第一层存在2倍频、3倍频、4倍频、5倍频、6倍频分别为 314.9 Hz,472.4 Hz,629.9 Hz,786.6 Hz,944.1 Hz。 此外在 157.5 Hz 两边出现了间隔为29.3 Hz的边频带。说明内圈损伤时存在对振动信号的调制。在第2,、第3层包络谱中故障特征频率倍频逐渐减少。
4)上述结果表明EMD包络分析能有效识别出非平稳、非线性信号中的故障特征频率,且系统操作简单,反应快速准确,具有良好的人机交互和强大的图形化显示界面。
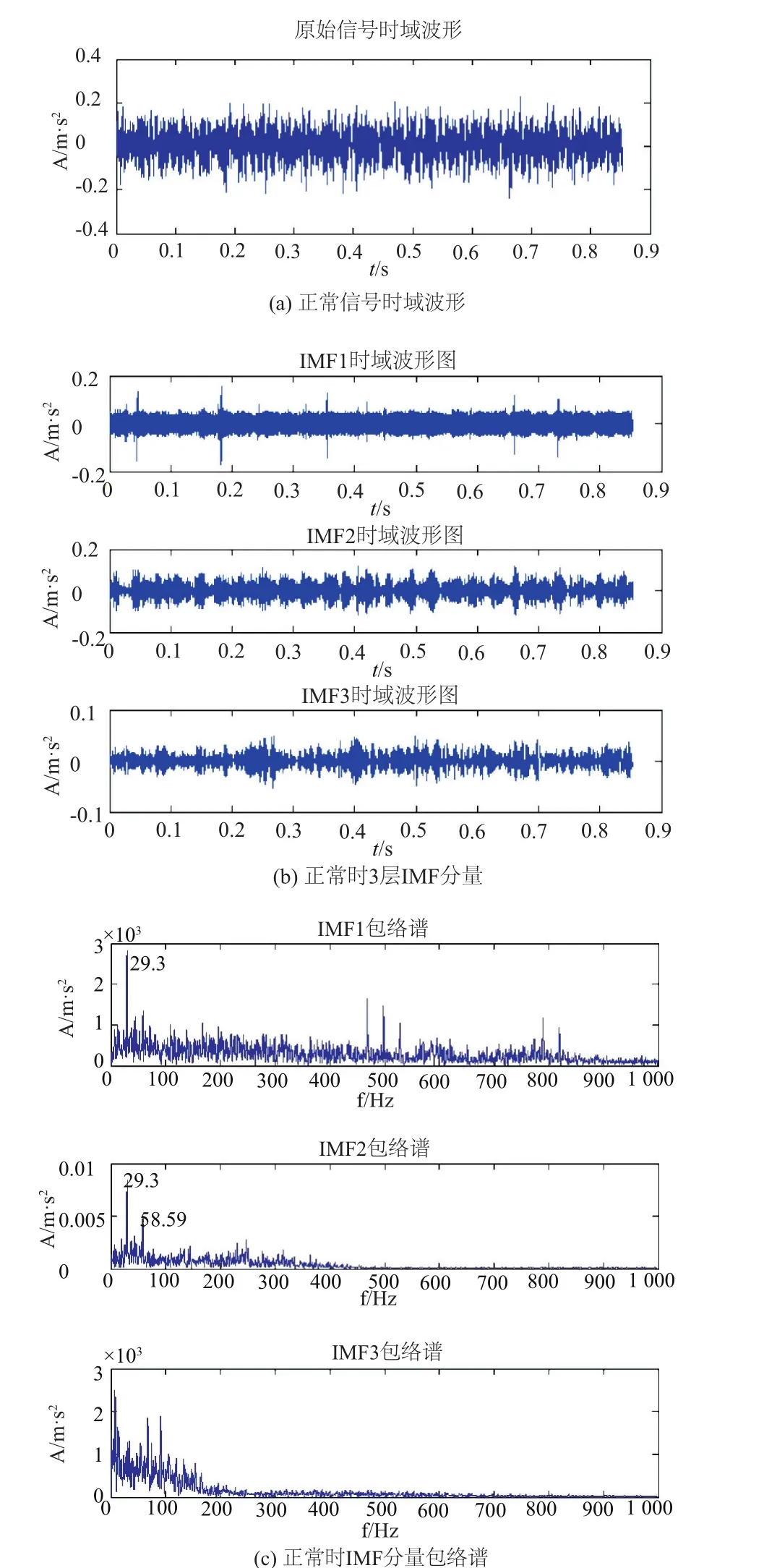
图4 正常时信号EMD包络分析


图5 内圈损伤EMD包络分析
5 结语
将Labview和Matlab优势互补,通过Matlab Script节点技术混合编程在虚拟仪器诊断系统中实现EMD包络谱分析。实例应用结果表明:Matlab提供的EMD包络能准确、快速的识别轴承正常和损伤时的非线性、非平稳信号,系统具有良好的人机交互界面和强大的图形显示界面,选择不同分层时只需在图2程序后面板中添加或减少类似subplot(311);plot(t,imf(1,:));xlabel('t/s');ylabel('a/m.s2');title('IMF1时域波形图'); 和 subplot(311);hua_baol(imf(1,:),fs,1,xf1,xf2);xlabel('f/Hz');ylabel('a/m.s2');title('IMF1包络谱')的语句即可。在工程中将Labview、Matlab和EMD包络三者结合起来在处理非线性、非平稳信号时具有广阔的应用价值。
[1]Norden E Huang,Zheng Shen,Steven R Long,etAl.The empirical modede composition and the Hilbert apectrum for nonlinear and nonstationary time series analysis[J].Proc R Soc Lond A,1998(454):903-995.
[2]于德介,程军圣.EMD方法在齿轮故障诊断中的应用[J].湖南大学学报(自然科学版),2002,29(6):48-51.
[3]唐贵基,马万里,胡爱军.EMD的LabVIEW实现及其在滚动轴承故障信号分析中的应用[J].轴承,2011(05):37-40.
[4]柴敬安,廖克俭,潘德惠,等.Labview和Matlab混合编程方法的研究与实现[J].计算机测量与控制,2008,16(5):737-740.
[5]徐明,于业明.LabVIEW中MATLAB的调用[J].山东理工大学学报(自然科学版),2005,19(4):92-95.
[6]李辉,郑海起,唐立伟.基于EMD和包络谱分析的轴承故障诊断研究[J].河北工业大学学报,2005,34(1):11-15.
[7]徐仁林,安伟.小波降噪在信号基于EMD的Hilbert变换中的应用[J].噪声与振动控制,2008(6):74-77.

