金属橡胶材料干摩擦阻尼的产生机理及力学模型

李宇燕,王炜

(1.西安工业大学机电工程学院,陕西西安710021)

(2.中国科学院西安光学精密机械研究所空间光学研究室,陕西西安710119)

金属橡胶材料属于多孔隙材料,受力后体积可变化,在金属橡胶材料的内部通过螺旋型金属丝相互摩擦接触来损耗振动能量。因此金属橡胶材料在刚度和阻尼上都不是线性的,其刚度跟制造工艺参数以及系统所受的载荷类型有关,其干摩擦阻尼受密度、编织形式等制造工艺参数影响也较大[1-4]。干摩擦阻尼、非线性刚度的产生机理以及计算模型较为复杂,尤其对金属橡胶材料而言,其内部存在大量的干摩擦接触,无法通过试验手段检查和区分出金属橡胶材料内部各个接触点的法向摩擦力以及弹性变形阻力,其内部大量的干摩擦接触点在载荷作用过程中,无法直接观测。因此,准确建立金属橡胶材料的力学模型是一个难题,需要对金属橡胶元件在不同载荷下的滞环回线进行深入地分析和研究。

众所周知,利用干摩擦元件的耗能机制来抑制结构的振动水平是一种非常有效的减振或隔振措施。但是,由于客观存在不光滑的非线性泛函本构关系,使得含有干摩擦环节的结构在简谐、随机和冲击激励下的响应计算问题非常困难。几十年来,国内外众多的学者对这一问题进行了系统深入的理论与实验研究,取得了丰硕的研究成果,为后人的继续研究奠定了坚实的基础[5,6]。目前,关于两固体接触表面间的干摩擦问题已经有了许多数学模型,其中振动工程中常用的摩擦力模型可分为四个主要类型,即关于相对滑动速度的不连续函数的Sgn摩擦模型和关于滑动位移的滞后连续函数的滞迟模型,这两种模型都是建立在整体滑动模型基础上的,另外,还有动态系统中干摩擦力的数值计算模型、三次非线性粘性阻尼双线性滞迟模型。

1 金属橡胶干摩擦阻尼的产生机理

在机械结构产生振动的过程中,当相互压紧的两个表面有滑动趋势或者出现相对滑动时,这两个表面之间就会产生一个抵抗继续滑动的反力,这就是干摩擦力,也称为库仑摩擦力。摩擦作用的最明显的后果之一是使物体振动的机械能转变为热能扩散于周围介质中,即产生能量转换,因而可达到减振的目的。由干摩擦力产生的耗能作用称为干摩擦阻尼,也称为库仑摩擦阻尼。金属橡胶材料在受到振动位移时,会由于金属丝间的摩擦、挤压和变形而耗散大量的振动能量,因此其可以归于库仑摩擦阻尼一类[2]。

库仑摩擦阻尼与物体表面的微观结构密切相关。肉眼看上去很光滑的工程表面,放在显微镜下观察时,会发现它是由许多个显然不规则的尖峰和凹谷所组成。当两个表面在载荷的作用下发生接触时,表面上多数微凸体的尖端处产生局部焊合,同时许多峰谷彼此啮合。若有一侧向力F施加于上表面使,两个表面,有相对滑动的趋势时,焊合处及啮合的峰谷间即产生阻力,只有当力F大于这些尖峰和焊合处的强度而产生剪切时,两表面才会产生相对滑动,这个剪切力就是这两个表面间的最大静摩擦力。物体表面产生相对滑移后,残存的和新生的峰谷在载荷作用下又会产生局部焊合和啮合,因此,接触面上仍然有阻力,这就是动摩擦力。一般情况下,滑动过程中焊合点和啮合峰谷数比静止状态时少,啮合得也比较浅,所以,动摩擦力比静摩擦力要小。由于时间、温度、运动历程(记忆效应)甚至湿度都会影响静摩擦力的大小,因此,从满足工程计算精度要求出发,可以忽略静摩擦力与动摩擦力之间的细微差别。以上虽然揭示了干摩擦阻尼的产生机理,但欲准确地揭示干摩擦阻尼的减振规律,必须正确地提出描述干摩擦规律的数学模型。

2 Sgn摩擦模型

1931年,Den Hartog提出了理想干摩擦模型(Coulomb摩擦模型)[7],即在一个具有干摩擦交接面的单自由度系统中,交接面上的干摩擦力是突然发生的,其时域波形为理想方波,并且干摩擦力总是阻碍运动,与运动速度反向摩擦力变化规律可表示为:

其中:Ff为摩擦力,μ为滑动摩擦系数,N为正压力,v为相对滑动速度。式(1)通常简写为:

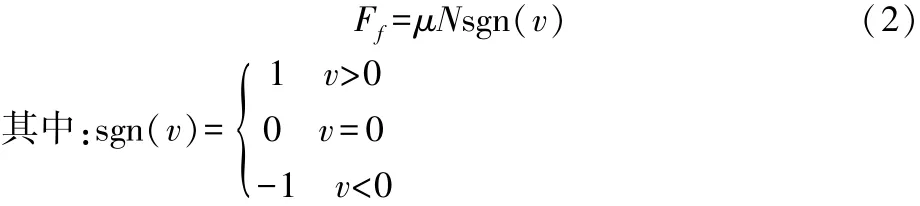
3 滞迟摩擦模型

实际上,干摩擦交接面都具有一定的弹性,在外力作用下,交接面先是沿切线方向产生弹性变形,等到外力大到一定程度,交接面才产生相对滑移。考虑到交接面的弹性性质,将干摩擦表面看成是一根弹簧和一个理想的Coulomb摩擦副串接,1961年,Iwan,Caughey等提出了著名的双线性滞迟恢复力模型[8]。其中,具有记忆特性的非线性恢复力z(t)采用双折线模型来近似描述,其增量形式的本构关系可表示为:

其中:ys为两固体接触表面发生宏观滑移时弹性变形的极限值,zs表示滑移时的记忆恢复力,y(t)是滞迟环节两端相对位移变形量。

4 动态系统中干摩擦力的数值计算模型

对受到干摩擦力作用的运动物体,有运动方程如下[1]:

其中:m为物体质量,v为运动速度,Rf为干摩擦阻力,F为除干摩擦力外的所有作用力的合力,fs为静摩擦力大为随速度大小变化的动摩擦力大小。式(5)称为干摩擦力的理论模型。

5 三次非线性粘性阻尼双线性滞迟模型

近年来,随着诸如钢丝绳、金属丝网、金属橡胶等新型干摩擦元件在隔振、减振领域日益广泛的应用,国内外学者对其本构关系、实验建模、响应计算、隔振减振性能指标、工程应用等方面展开了卓有成效的研究,大量试验结果表明,新型干摩擦元件的记忆特性可以用双折线模型或一阶微分方程模型来描述。一般新型干摩擦元件的本构关系可以分解为有记忆环节和无记忆环节的并联,即变形后的恢复力gn,可分解为两部分g0和z。而g0代表与当前变形状态有关的无记忆部分,z代表与整个变形历史有关的记忆部分[1],其关系式为:

一般无记忆恢复力是变形状态的二元函数,其常见形式是二元多项式[1],表达式为:

尽管无记忆恢复力的一般表达式(8)比较复杂,但以往钢丝绳等减振器的工程试验结果表明,无记忆恢复力的立方非线性成分是主要的支配因素。因此,可以用含有立方非线性粘性阻尼双线性滞迟模型来近似描述,以满足工程应用的精度要求。为此,白鸿柏、黄协清提出了三次非线性粘性阻尼双线性滞迟模型[5,6]。图1建立的力学模型代表了简化为集中质量的设备与诸如钢丝绳等干摩擦非线性减振器相联并固定在刚性基础之上时的隔振问题。图2为干摩擦非线性减振器具有记忆特性的双折线泛函关系。

图1 力学模型

图2 双折线本构关系

图1和图2中,zs,ks,ys分别为干摩擦非线性减振器环节滑移后的恢复力、未滑移前的线性刚度、滑移极限,Δ为环节的相对滑移量。由图1可写出滞迟振动系统运动方程为:

引入如下变量:

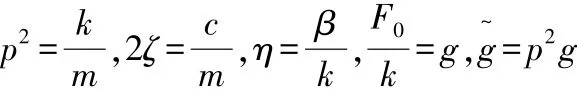
则式(9)变为:

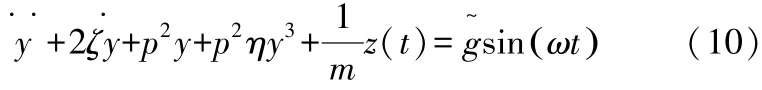
对于式(9)可以用谐波平衡法求解。

6 结语

在金属橡胶材料的内部通过螺旋型金属丝相互摩擦接触来损耗振动能量,干摩擦阻尼、非线性刚度的产生机理以及计算模型是一个较为复杂的问题。本文从微观的角度分析了金属橡胶材料干摩擦阻尼的产生机理。建立金属橡胶材料的力学模型,需要对金属橡胶元件在不同载荷下的滞环回线进行深入地分析和研究。几十年来,国内外众多的学者对这一问题进行了系统深入的理论与实验研究,本文简要介绍了四种数学模型,即Sgn摩擦模型、滞迟模型、动态系统中干摩擦力的数值计算模型、三次非线性粘性阻尼双线性滞迟模型。

[1]宋凯.金属橡胶非线性离散结构单元模型的理论与试验研究[D].西安:西安交通大学,2004.

[2]刘桥.金属橡胶材料的非线性特性及其在航天减振器中的应用[D].西安:西安交通大学,1997.

[3]李宇燕.金属橡胶材料的非线性本构关系及系统振动响应的研究[D],西安:西安交通大学,2006.

[4]张俊华.金属橡胶材料物理机械性能及阻尼特性理论与应用研究[D].西安:西安交通大学,1999.

[5]白鸿柏,黄协清.干摩擦非线性减振器构成的迟滞振动系统的响应计算[J].机械工程学报,1998,34(5):70-75.

[6]白鸿柏.干摩擦振动系统响应计算方法[D].西安:西安交通大学机械工程学院,1998,8-24.

[7]Den Hartog J P.Mechanical Vibrations[M].New York:MeGrraw－Hill Book Company, Inc., 4THed., 1956,20(1):421-425.

[8]Iwan,Caughey.The Dynamic Response of Bilinear Hysteretic System[D].California:California Institute of Technology,1961:37-45.