固体发动机中轴对称界面端应力奇异性研究①
顾志旭,郑 坚,彭 威,殷军辉
(军械工程学院火炮工程系,石家庄 050003)
固体发动机中轴对称界面端应力奇异性研究①
顾志旭,郑 坚,彭 威,殷军辉
(军械工程学院火炮工程系,石家庄 050003)
从界面防护的角度出发,研究了温度载荷下固体发动机中弹性-粘弹性轴对称界面端的奇异应力场。依据对应原理,由弹性-弹性界面端的特征方程获得了弹性-粘弹性界面端的应力奇异性指数。根据应变匹配模型,推导了温度载荷下轴对称界面端中的常应力项。针对现有的应力释放罩/推进剂界面端,分析了材料参数和结合角对其应力奇异性指数的影响规律,在不改变装药量的前提下,提出了弱奇异性或无奇异性界面端的设计。结果表明,自由边呈平角时界面端至多存在-0.1的弱奇异性,界面端应力集中水平显著降低。
固体发动机;轴对称界面端;奇异应力场;常应力项
0 引言
固体发动机燃烧室内通常存在着壳体/绝热层、绝热层/包覆层、包覆层/推进剂等多个界面。界面失效是发动机结构完整性破坏的主要形式之一。从固体力学的角度而言,粘结强度和应力水平是影响界面粘结质量的两大决定性因素,当界面应力超过界面的粘结强度时,界面发生破坏。界面的粘结强度依赖于结合材料的理化性能和工艺条件,而界面应力主要取决于结构部件的构型和负载工况。结合材料成型后,不考虑老化损伤时,界面的失效主要取决于界面的应力水平。
针对固体发动机中界面脱粘问题,国内学者从界面应力的角度出发,开展了一系列的研究。史宏斌等[1]分析了内聚空洞对推进剂/衬层界面应力的影响。杨月诚等[2]讨论了发动机充气内压对药柱/壳体界面应力的影响。郑晓亚等[3]研究了固体装药在挂飞工况下,壳体/绝热层界面应力的分布规律。上述研究主要关注了应力在整个界面上的分布,而忽视了界面端应力场的奇异性。大量研究表明,界面端的奇异应力场是诱发界面破坏的主要因素[4-5]。
本文针对发动机中的应力释放罩/推进剂(弹性/粘弹性)轴对称界面端,分析了界面端奇异应力场随材料性能和结合角的变化规律,进一步提出了弱奇异性或无奇异性界面端的设计,所得结论可为发动机界面设计提供一定参考。
1 界面端奇异应力场
1.1 固体发动机中的界面端
某型固体发动机主要有壳体、绝热层、包覆层、推进剂及应力释放罩组成,如图1所示。
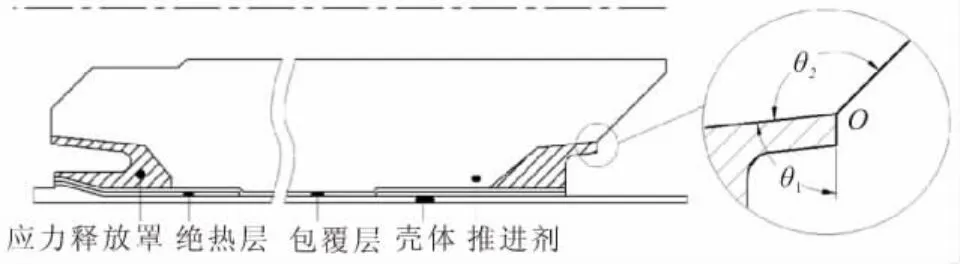
图1 固体发动机结构Fig.1 Structure of solid motor
应力释放罩一般由包覆层材料成型,与推进剂因发生组分迁移和水解反应而较易脱粘[6]。若将包覆层视为弹性材料,则应力释放罩/推进剂界面端为典型的弹性-粘弹性轴对称界面端。
1.2 弹性-弹性界面端
当两相弹性材料形成图2所示的平面界面端时,O点附近的应力场具有以下分布特征[7]:
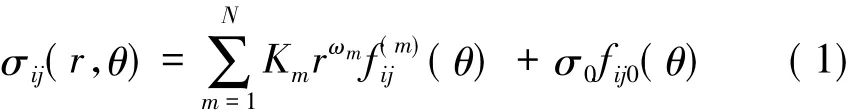
式中 r,θ为以 o点为原点的极坐标;Km为与结合角θ1和 θ2、材料常数及外载有关的应力强度系数;ωm和(θ)为应力奇异性指数和应力角分布函数;σ 为热0载荷作用时附加的常应力项;N为奇异性指数的数目。
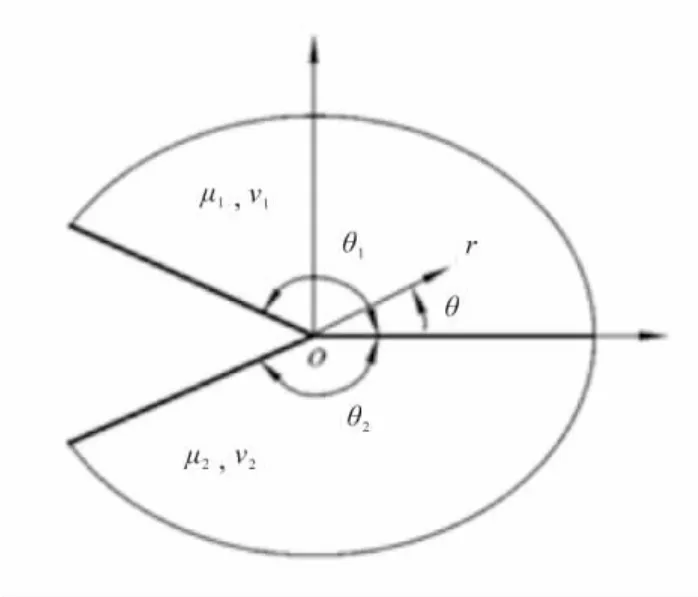
图2 平面界面端Fig.2 Plane joint
式(1)中,应力强度系数K和应力奇异性指数ω是决定应力场应力水平的主要参数。应力强度系数K不能解析表达,一般由数值结果拟合获得。应力奇异性指数ω仅与材料参数和结合角有关,一般由特征函数展开法[7]、Mellin 变换法[8]或复应力函数法[4]建立的如下特征方程解得22

式中 λ为方程的特征值;α和β为Dundurs参数;κ在平面应力时为(3-4ν)/(1+ν),平面应变时为 3-4ν;Γ为剪切模量μ2/μ1之比;ν为泊松比;下标表示材料1、2,下同。
通常,特征方程(2)存在着多个特征根,当且仅当0<Re(λm)<1时(Re表示取实部),界面端的应力场才具有奇异性,此时有

若特征方程只具有一个奇异特征值,对式(1)取对数,有
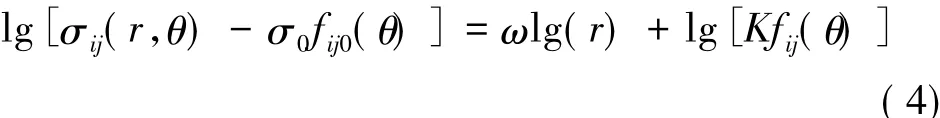
可见,在双对数坐标下,应力与极径呈线性关系,且应力奇异性指数为拟合直线的斜率。
1.3 弹性-粘弹性界面端
粘弹性材料的性能与时间相关,由其组成的界面端的应力奇异性指数ω必然也与时间相关。在理论上,求取应力奇异性指数时,需要借助于特征方程,而基于弹性-粘弹性对应原理,可直接由弹性-弹性界面端的特征方程变换获得弹性-粘弹性界面端的特征方程。
为便于实施变换,将粘弹性材料的松弛模量简化为
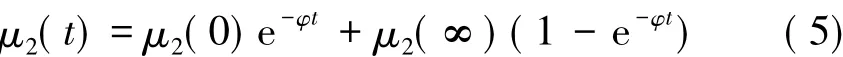
式中 μ2(0)、μ2(∞)分别为初始模量和持久模量;1/φ为松弛时间。
假定粘弹性材料的泊松比为常数,由对应原理可得[9]
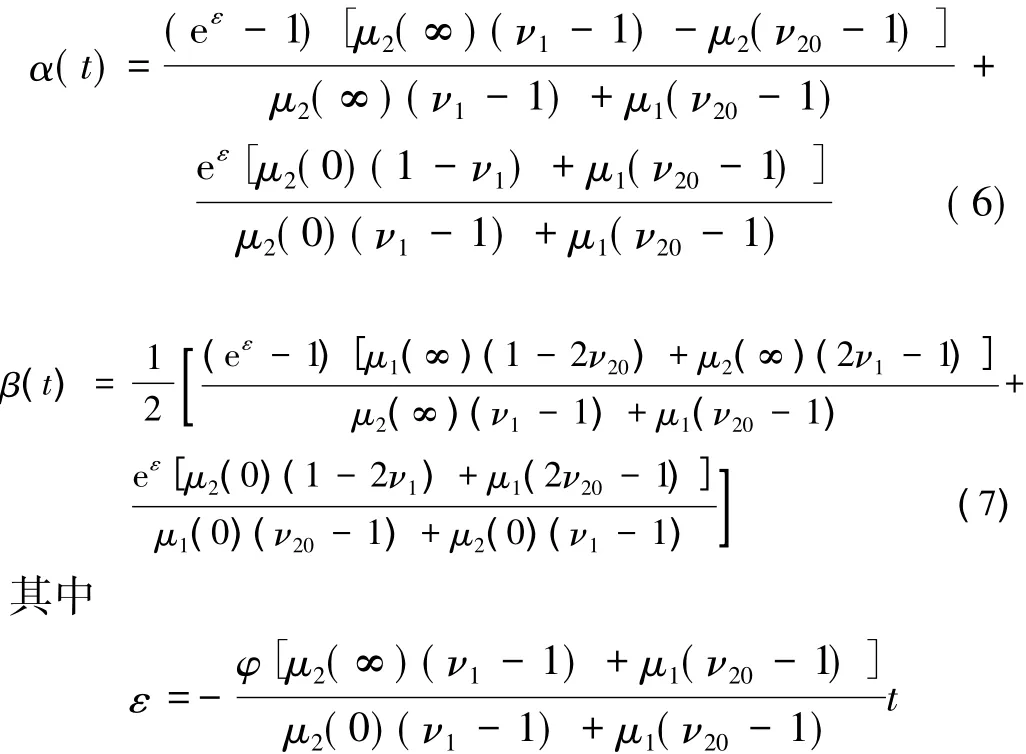
1.4 轴对称界面端的常应力项
研究表明,轴对称界面端和对应平面应变界面端具有相同的应力奇异性指数[10],但常应力项σ0不同。Munz[7]指出常应力项对奇异应力场的分布具有重要的影响,并给出了平面问题下的解析表达式。然而,对于图3所示的轴对称界面端,尚未查阅到有关常应力项的报道。
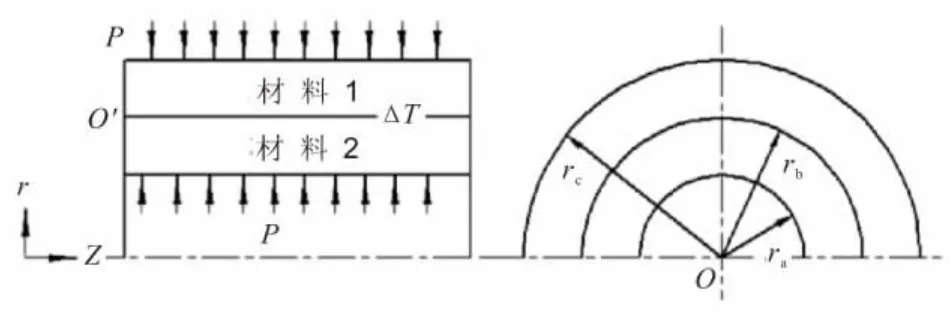
图3 轴对称界面模型Fig.3 Axisymmetric interface model
Blanchard和 Ghoniem[11]在研究平面界面端的奇异热应力场时,提出了应变匹配模型,即奇异点处的应变在热应力和常应力项的共同作用下相互匹配。可验证,基于此模型可便捷地推导获得文献[7]中的常应力项[12]。因此,本文假定轴对称界面端也符合应变匹配模型,在求得常应力项后,用数值方法进行验证。
对于图3中的轴对称界面端,应变匹配模型假定,两相材料在界面处光滑接触,同时在内外表面受压力P的作用。在温度ΔT和压力P的共同作用下,奇异点O′处径向应变相等,且此时的压力P就为界面端在温度载荷作用时的常应力项。
依据弹性理论,轴对称应力具有以下分布特征
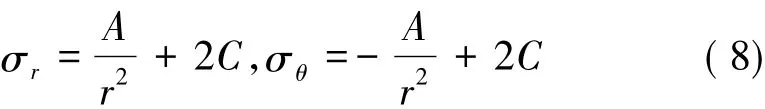
式中 A、C为待定参数。
由应力边界条件得

对图3中的模型,取表1中的材料组合,分析其在ΔT=-103℃下O′点处径向应力的分布。其中,ra、rb和 rc分别为 100、200、300 mm。
边界修正的基本思路是对聚类边界的稀疏网格单元做进一步划分,考察其子单元是否满足一定条件,将满足条件的子单元合并到相邻的稠密单元,补全聚类边界。该方法针对CLIQUE算法采用固定宽度划分的缺点,对所有位于聚类边界的稀疏网格单元进行处理,将它们等分为2n个子单元,统计每个子单元中数据点的数量,判断这些子单元的密度是否大于或等于给定的密度阈值且紧邻于某一个稠密单元,如果条件成立,则将子单元合并到邻近的稠密单元,否则不作处理。具体步骤如下:
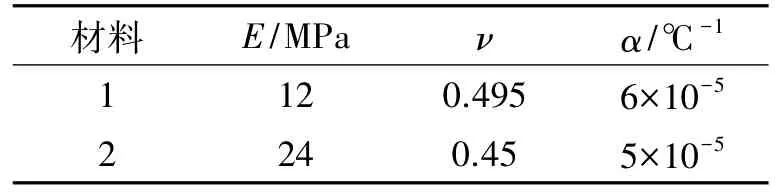
表1 材料组合Table 1 Material combination
由特征方程求得的应力奇异性指数ω=-0.08,式(13)解得的常应力项σ0=-0.034 MPa。依据式(4)作图4,图中离散点为对数应力值,实线为拟合直线,下同。
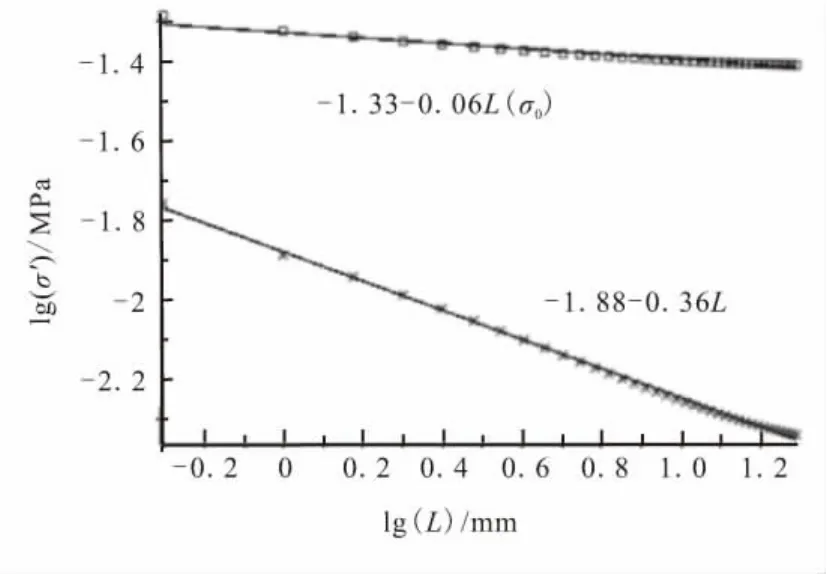
图4 界面应力分布Fig.4 Interfacial stress distribution
图4给出了考虑和不考虑常应力项σ0时的应力分布曲线。由图4可知,无σ0时拟合直线的斜率为-0.36,含 σ0时为-0.06,而理论值为-0.08。可见,考虑常应力项σ0时,式(1)能较好地表征界面端应力场的奇异特性,同时也说明,基于应变匹配模型获得的轴对称常应力项具有一定的准确度。
在弹性-粘弹性轴对称界面端中,温度载荷下的常应力项可依据对应性原理由式(13)求得,拉氏逆变换时,可采用近似的方法处理[13]。
2 应力释放罩/推进剂界面端奇异指数研究
材料参数和结合角是影响界面端应力奇异性指数的两大决定性因素,降低应力奇异性指数(应力集中程度),需要从以上2个因素予以考虑。
2.1 材料参数的影响
应力释放罩/推进剂界面端的初始结合角为84°/141°(见图1),此时奇异特征值的分布见图5。
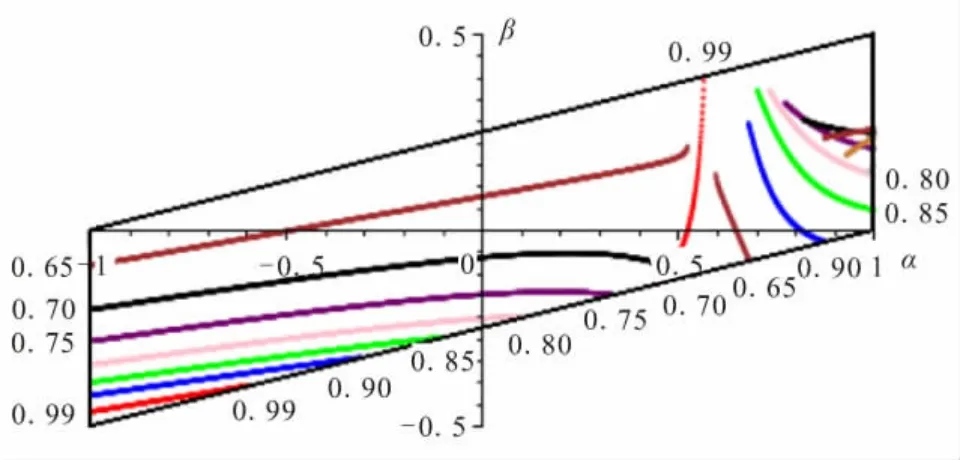
图5 奇异特征值分布Fig.5 Singular eigenvalue distribution
由图5可见,结合角为84°/141°时,在大部分材料组合下界面端应力存在着奇异性,且当α<0.5时,奇异特征值随β的增大而减小,应力奇异性增强,当α>0.9时,奇异特征值随着β的增大而减小。只有当α接近0.54时,奇异特征值约为0.99,应力奇异性基本消失,此时的材料组合为最佳组合。
根据厂家提供的材料数据以及应力释放罩材料性能与推进剂相近的原则[14],给出应力释放罩/推进剂界面可能的材料组合范围:Γ∞∈(0.1,10)且ν1∈(0.45,0.5)。其中,Γ0/Γ∞=5,Γ0=μ2(0)/μ1,Γ∞=μ2(∞)/μ1。此时,由式(6)和式(7)确定的 Dundurs参数的分布如图6所示。
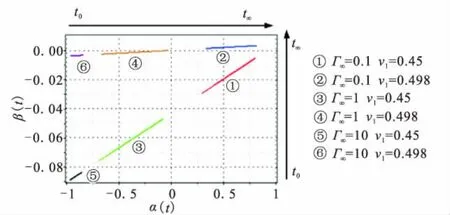
图6 Dundurs参数的分布Fig.6 Dundurs parameters distribution
在图6中,曲线的左右端点分别对应初始时刻t0与持久时刻 t∞。由图6可知,当 Γ∞∈(0.1,10)时,α∈(-1,1)且 β∈(-0.09,0.003),同时 α 和 β 均随时间的增加而增大。泊松比ν1增大时,β绝对值有所增加,但即使 ν1=0.5 时,β 也不大于 0.004。因此,在应力释放罩/推进剂界面可能的材料组合范围内有α∈(-1,1),且 β∈(-0.09,0.004)。此时,奇异特征值的分布见图7。
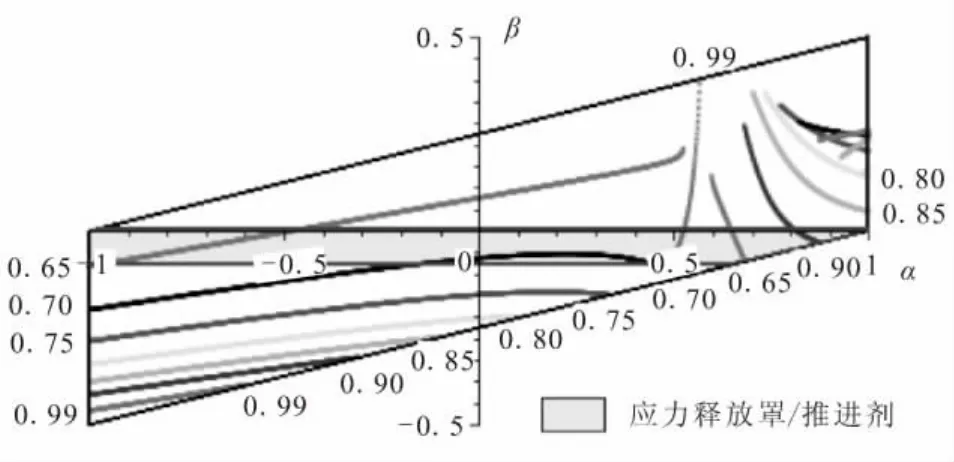
图7 应力释放罩/推进剂界面端特征值的分布Fig.7 Eigenvalue distribution of cover/propellant joint
由图7可见,在可能的组合范围内(图中阴影区域),界面端在大部分材料组合下具有-0.35~-0.3的奇异性,少数组合下(α≈0.54)无奇异性或只有弱奇异性(弱奇异性指λ>0.9)。考虑到奇异性指数的时间相关性,可知84°/141°的界面端难以长久保持无奇异或弱奇异的应力状态,应力集中的现象难以彻底消除,界面破坏的几率依然较高。
2.2 结合角的影响
在应力释放罩/推进剂界面端中,改变结合角θ2会影响发动机的装药量,故只调整结合角θ1。θ1增大时界面端趋于界面裂纹,应力奇异性增强,趋近于-0.5,θ1减小时,奇异特征值的变化见图 8。
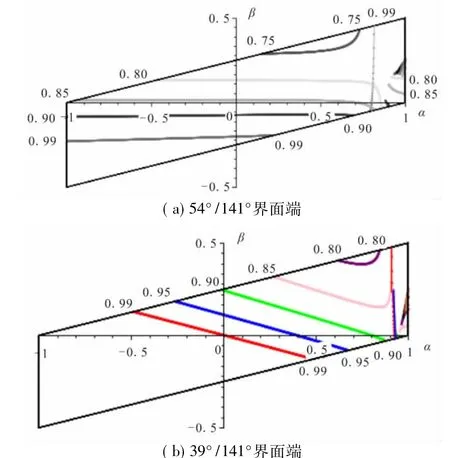
图8 界面端奇异特征值分布Fig.8 Singular eigenvalue distribution of joint
图8给出了结合角θ1为54°和39°时,奇异特征值的分布图。由图8可见,奇异特征值随着θ1的减小而整体向第一象限移动。当θ1减小为39°时,第三象限无实特征值,第四象限的特征值几乎不小于0.9。此时,复奇异特征值的分布如图9所示。
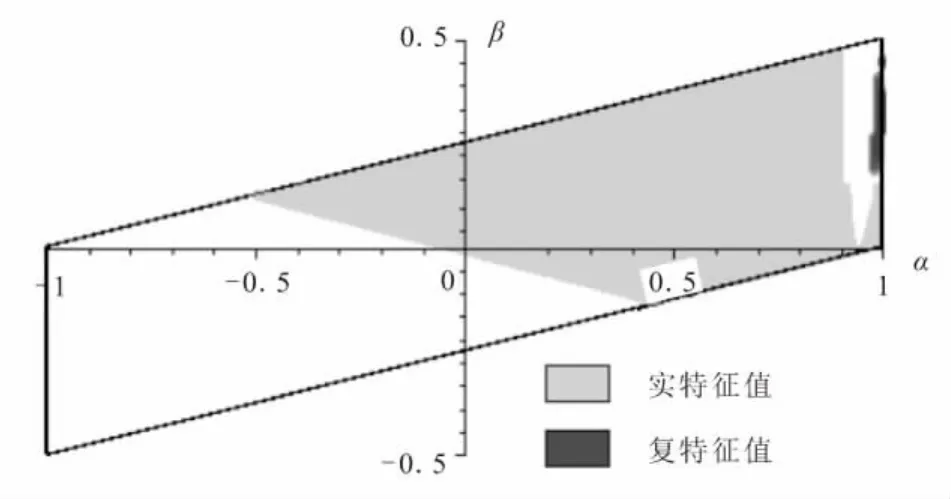
图9 39°/141°界面端特征值的分布Fig.9 Eigenvalue distribution of 39°/141°joint
由图9可见,实特征值的分布与图8(b)吻合,复特征值仅分布在第一象限。结合图7知,在不改变发动机装药量的前提下,当θ1减小为39°,界面端自由边呈平角时,在可能的材料组合下,界面端应力场在任意时刻至多具有-0.1的弱奇异性。当材料组合满足α<0时,界面端无奇异性。θ1继续减小时,第四象限内的特征值继续增大,应力奇异性继续消除。但此时奇异性的微小变化对应力值的影响甚微。因此,认定平角界面端为最佳设计。
2.3 数值验证
为了验证上述结论,下文计算低温-45℃环境中,84°/141°和 39°/141°设计下,应力释放罩/推进剂界面端的奇异应力场。计算时采用子模型法,以获取较为精确的应力值。在非直角轴对称界面端模型中,采用应变匹配模型,求取温度载荷下的常应力项存着困难,此处仍采用图3中的模型对常应力项作近似处理。
相关几何尺寸见表2,低温-45℃下材料参数见表3。

表2 几何参数Table 2 Geometry parameters
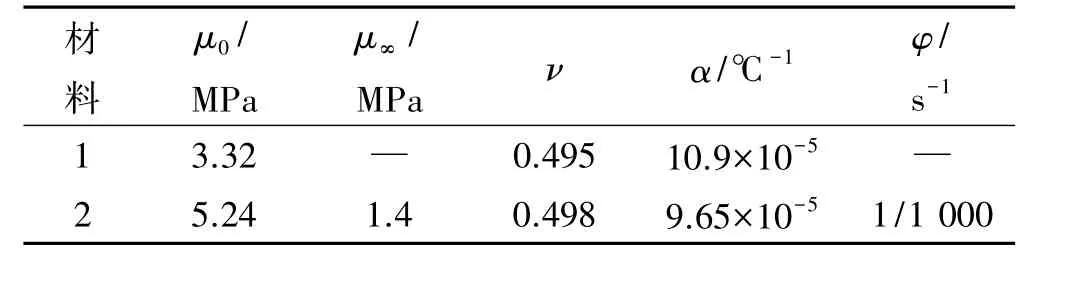
表3 材料参数Table 3 Material parameters
限于篇幅,文中仅给出t=3 000 s时,极坐标下界面前段正应力的分布,见图10。
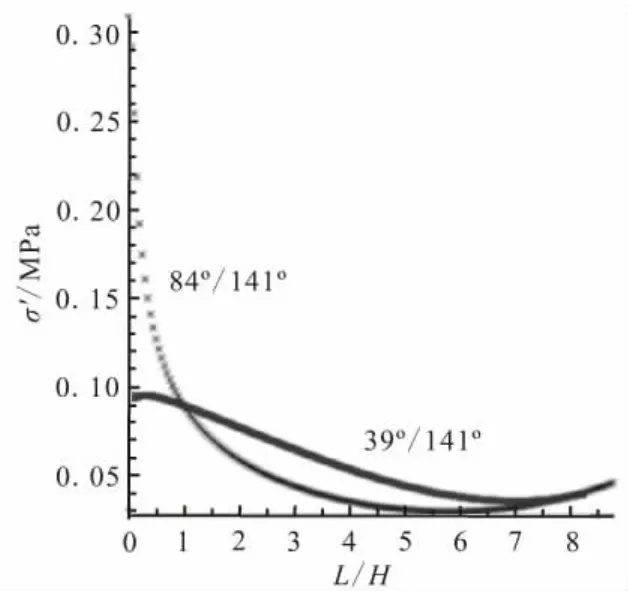
图10 界面正应力分布Fig.10 Normal stress distribution on interface
由图10可见,θ1分别为84°和39°时,界面端的最大拉应力分别为 0.31 MPa 和 0.1 MPa,84°界面端应力集中的程度明显强于39°的界面端。此外,虽然在1<L/H<7(H=5mm)段,39°界面端的应力值高于 84°的界面端,但因奇异点(L=0)的应力在界面的破坏中占主要地位,39°界面端的设计仍优于84°的设计。
双对数坐标下界面正应力的分布如图11所示。
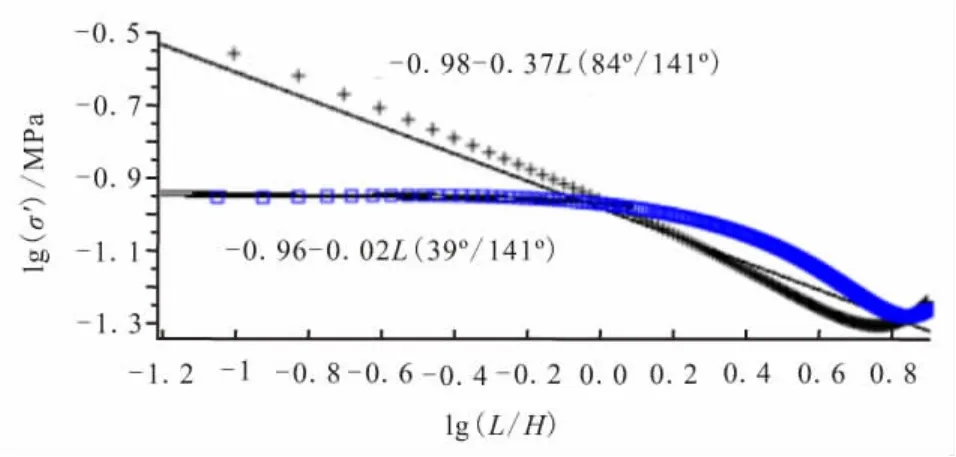
图11 界面正应力分布Fig.11 Normal stress distribution on interface
由图11可知,当结合角由84°减小为39°时,应力奇异性指数由-0.37 减小为-0.02,而理论值由-0.4减小为0,变化规律基本符合图8。注意到在lg(L/H)=0处两拟合直线相交,这表明结合角由84°减小为39°时,应力强度系数并未增大。此外,从图10和图11可看出,距界面奇异点约35 mm处,不同结合角下应力分布曲线相互重合,这说明结合角的变化对界面端以外区域(L≥35 mm)的应力场几乎无影响。因此,有必要将应力释放罩/推进剂的界面端设计为平角形式,而不必考虑其对远场的不利影响。
3 结论
(1)基于应变匹配模型推导的常应力项具有一定的准确度,可用来描述温度载荷下轴对称界面端的奇异应力场。
(2)当应力释放罩与推进剂材料相近时,界面端Dundurs参数 α∈(-1,1),且 β∈(-0.09,0.003)。在84°/141°的原始设计下,界面端应力场存在着-0.3~-0.35 的奇异性。
(3)应力释放罩的结合角减小至39°时,界面端应力场在任意时刻至多存在-0.1的弱奇异性,界面端应力集中的现象得以消除,界面应力破坏的几率降低。
[1]史宏斌,侯晓,朱祖念.含缺陷药柱人工脱粘层前缘应力分析[J].固体火箭技术,1999,22(3):47-49.
[2]杨月诚,张宁,强洪夫,等.固体火箭发动机卧式贮存状态界面应力数值分析[J].上海航天,2007(3):50-53.
[3]郑晓亚,柳青,王卫祥.固体装药结构界面应力分析[J].航空动力学报,2012,27(8):1861-1866.
[4]许金泉.界面力学[M].北京:科学出版社,2006.
[5]Kay N,Barut A,Madenci E.Singular stresses in a finite region of two dissimilar viscoelastic materials with traction-free edges[J].Computer Methods in Applied Mechanics and Engineering,2002,191:1221-1244.
[6]阮崇智.大型固体火箭发动机研制的关键技术[J].固体火箭技术,2005,28(1):23-28.
[7]Munz D,Fett T,Yang Y Y.The regular stress term in bonded dissimilar materials after a change in temperature[J].Engineering Fracture Mechanics,1993,44(2):185-194.
[8]Yang Y Y,Munz D.Determination of the regular stress term in a dissimilar materials joint under thermal loading by the Mellin transformation[J].Journal of Thermal Stresses,1994,17:321-336.
[9]Chowdhuri M A K,Xia Z.An analytical model to determine the stress singularity and critical bonding angle for an elasticviscoelastic bonded joint[J].Mech.Time-Depend Master,2012,6:343-359.
[10]Liu Y H,Xu J Q,Ding H J.Order of singularity and singular stress field about an axisymmetric interface corner in threedimensional isotropic elasticity[J].International Journal of Solid and Structures,1999,36:4425-4445.
[11]Blanchard J P,Ghoniem N M.An eigenfunction approach to singular thermal stresses in bonded strips[J].Journal of Thermal Stresses,1988,12:501-527.
[12]Gu Z X,Zheng J,Peng W,et al.Metohd to obtain the regular term in bonded dissimilar materials under thermal loading[J].Applied Mechanics and Materials,2013,395-396:802-805.
[13]Schapary R A.Approximate methods of transform inversion for viscoelastic stress analysis[C]//Proceedings of the Fourth US National Congress on Applied Mechanics,1962,2:1075-1085.
[14]王元有.固体发动机设计[M].北京:国防工业出版社,1984.
(编辑:崔贤彬)
Study of singular stress fields around axisymmetric joints in solid motor
GU Zhi-xu,ZHENG Jian,PENG Wei,YIN Jun-hui
(Department of Artillery Engineering,Ordnance Engineering College,Shijiazhuang 050003,China)
Singular stress fields around axisymmetric elastic-viscoelastic joint under temperature loading in solid motor were studied for the purpose of interface protection.The singular exponent of elastic-viscoelastic axisymmetric joint was obtained from the eigenvalue equation of elastic-elastic joint based on the elastic-viscoelastic correspondence principle.The regular stress term of axisymmetric joint under temperature loading was deduced on the basis of the strain match model.Aimed at the original design of stress release cover/propellant joint,the effects of bonded material parameters and bonded angular on stress singular exponent were analyzed,and the weak singularity or without singularity design of joint was put forward on the condition that the charge will not be changed.Results show that there is one about-0.1 week singularity at most when the free edges of joint form a straight angle,the stress concentration level will be declined obviously.
solid motor;axisymmetric joint;singular stress fields;regular stress term
V438
A
1006-2793(2014)04-0510-06
10.7673/j.issn.1006-2793.2014.04.015
2013-09-29;
2013-10-22。
顾志旭(1988—),男,硕士,研究方向为固体发动机结构完整性分析。E-mail:lemberry@163.com

