改性双基推进剂高应变率Ⅱ型断裂力学行为①
赵 超,郑 健,鞠玉涛,张君发,汪文强
(南京理工大学机械工程学院,南京 210094)
改性双基推进剂高应变率Ⅱ型断裂力学行为①
赵 超,郑 健,鞠玉涛,张君发,汪文强
(南京理工大学机械工程学院,南京 210094)
使用紧密剪切试件,借助霍普金森压杆、万能材料实验机和高速摄影设备,研究了改性双基推进剂材料在高应变率条件下的断裂能、断裂韧性及裂纹传播路径。实验结果表明,改性双基推进剂材料在准静态条件下表现出明显的粘弹性,而在高应变率条件下表现出脆性。通过分析计算得到了紧密剪切试件在不同应变率下剪切面应力应变关系的变化规律、裂纹传播路径,以及1 000 s-1应变率下材料的断裂能、断裂韧性等力学参数。
改性双基推进剂;紧密剪切试件;高应变率;断裂能;动态断裂韧性;裂纹扩展路径
0 引言
改性双基推进剂由于其具有能量密度高、燃速快、强度高等优点,成为火炮发射用火箭发动机常用装药。作为高分子聚合物,其力学特性表现出明显的粘弹性,在准静态和高应变率条件下差异非常明显。近年来,许多学者对该材料在准静态下的力学性能进行了研究,并给出相关的松弛模量、本构方程等[1]。王蓬勃等[2]应用朱王唐模型研究了高应变率下改性双基推进剂的本构方程。结果表明,朱王唐模型能够很好地描述材料动态力学特性。但这些研究并未对材料在工程中的实际应用特性做出讨论,如改性双基推进剂产生裂纹或发生断裂,常常是引起火箭发动机在点火后发生爆炸的主要原因[3]。因此,研究该材料在高应变率下的断裂性能对于固体火箭发动机,尤其是火炮发射用火箭发动机工程应用是非常重要的。
目前,对于高应变率下材料的动态力学行为的研究,最为简单且精确的实验设备是分离式霍普金森杆。其原理是在所研究试件的两端建立动态的力平衡,通过分析入射波、反射波和透射波的变化,来研究相关材料的动态力学行为。本文利用这一方法,研究了改性双基推进剂的II型断裂力学行为,从而为这类发动机装药结构力学分析提供支持。
1 实验
如图1所示,实验采用分离式霍普金森杆装置。该系统由2根材料相同、直径相等的弹性杆(首先被加载的杆为入射杆)构成;加载由子弹的撞击产生,子弹的材料以及直径与杆相同,长度由所需的波长决定;被测试件夹在两杆之间,子弹撞击入射杆后在入射杆中形成压缩波εinc,入射波的一部分在入射杆端面反射后形成拉伸波εref,其余部分穿过试件,在透射杆中形成透射波 εtra。
实验中,为了满足应力波在试件以一维形式传播,且试件中应力应变均匀分布,一般把试件做成厚度很薄且直径很小的圆柱。符合上述要求后,一旦测得试件与入射杆和透射杆界面处的应力和质点速度,就可得到名义应力σ(t)和纵向应变率l(t):

这样,被测材料的动态力学行为就可通过将入射波、反射波和透射波代入上面的3个方程得到。本研究采用了14 mm分离式霍普金森杆实验装置,根据改性双基推进剂弹性模量小的特点及模量匹配问题,采用LC4铝制杆。入射杆长2 000 mm,反射杆长2 000 mm,子弹长400 mm。
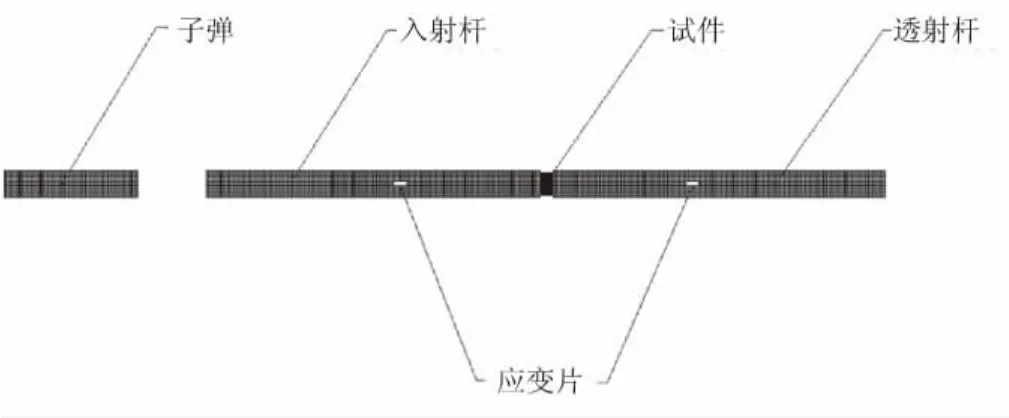
图1 分离式霍普金森实验装置Fig.1 Split hopkinson pressure bar experiment device
Ⅱ型断裂研究所用试件选择Watkins J所提出的紧密剪切试件[4]的几何特征,该几何特征的试件已被许多学者采用,并进行了多种材料 II型断裂的研究[5-6]。为了使紧密剪切试件(以下称为试件)配合分离式霍普金森杆装置,将试件做成圆柱形凸台加预制裂纹的形式,其加工成品如图2所示:先将改性双基推进剂材料加工成直径和高都为h的圆柱,h的取值应小于等于霍普金森杆各个杆的直径,在这里 h=14 mm,等于杆的直径。在圆柱一个端面加工宽度为d、深度为(a-1)mm的通槽;另一个端面加工宽度为d、高度为(a-1)mm 的凸台,这里 a=5 mm,d=5.6 mm;最后,在通槽底面两侧分别预制宽0.4 mm、深1 mm的裂纹。上述尺寸取值使试件两端的受力面积相等,从而保证了试件中应力与应变的均匀系数相等[7],这为后面所提出的受力假设提供了理论依据。试件加工成型后高温50℃、24 h去残余应力,实验在常温下进行。
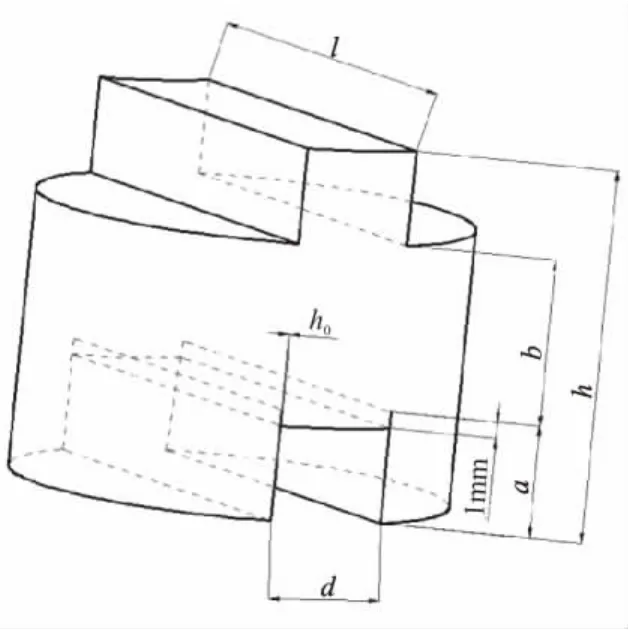
图2 试件的加工成品示意图Fig.2 Schematic diagram of the finished product specimen
试件加工成图2所示几何形状的目的是使其发生剪切失效,本文根据Georges Challita和Ramzi Othman给出的有限元计算结果[7],对试件的受力作以下假设(如图3所示):
(1)该试件在受力时形成2个以剪切力为主的线性区域(如图3所示),定义该面为剪切面,其厚度为受到剪切力作用的平均宽度;
(2)定义试件的剪切面(如图3所示)为分离式霍普金森杆的作用面,当剪切面上的应力达到最大值时,试件发生初始断裂。
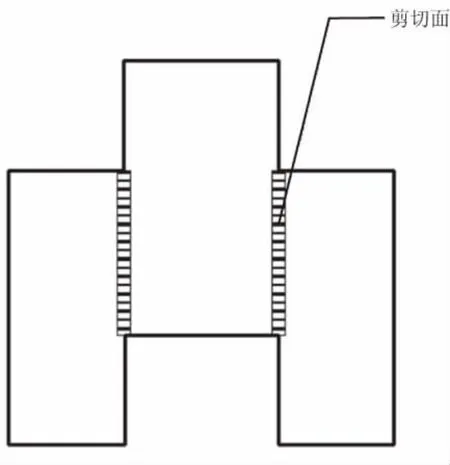
图3 试件受力的假设Fig.3 Assumption of force applied on specimen
由此,可将剪切应力、剪切应变率和剪切应变做出如下定义:
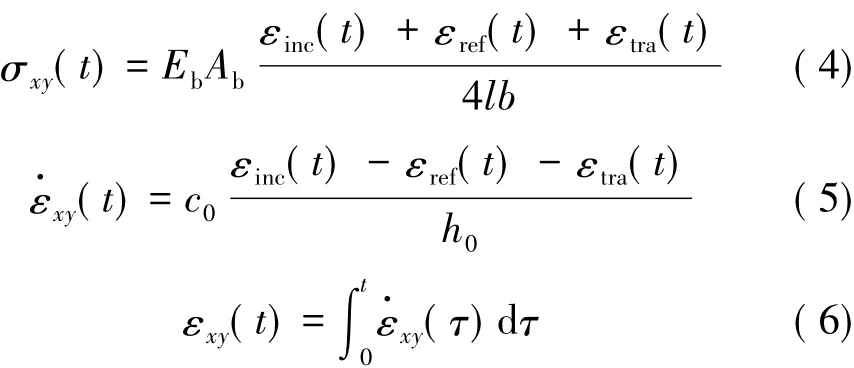
式中 l和b分别为剪切面的宽度和高度;h0为剪切面的厚度。
式(4)中,剪切面积2lb代替了压缩实验试件的横截面积As,剪切面厚度h0代替了试件长度ls。
为了得到试件发生断裂后试件2个碎片的动能,实验借助了高速摄影设备来获得试件的断裂过程。通过比较一系列照片中试件发生断裂后碎片位置和角度的变化,可计算得到碎片的飞行速度与转动速度。这样就得到碎片总动能和改性双基推进剂材料的断裂能。另外,在整个实验过程中,试件与两杆的接触面采用润滑油润滑以减小摩擦,该措施减少了能量损耗,使获得的断裂能更为准确。
2 实验结果及分析
图4所示为试件两端的应力随时间的变化曲线。从图4可看出,入射杆和透射杆上的应变片获得的“透射波-反射波”与“入射波”几乎相同,意味着试件两端产生的应力相同,证明了高应变率下实验符合实验基本要求,即试件在加载过程中应力动态平衡。同时,实验增加了2 mm/min的静态压缩实验来比较试件静态和动态加载条件下试件失效形式的异同。
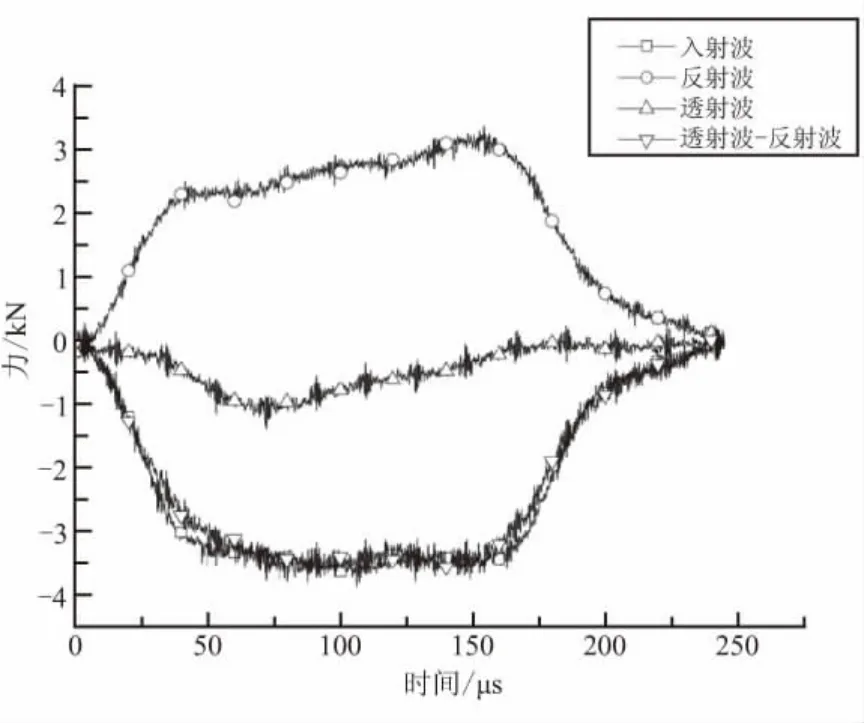
图4 试件两端的应力状态Fig.4 The stress state at the ends of the specimen
图5(a)和5(b)分别为试件在动态和静态加载下发生断裂后的照片。两图对比可明显反映出试件在不同受力条件下失效形式的差异。比较试验前后试件,可知动态加载断裂的试件各尺寸基本没有发生变化,如图5(a)所示;而静态加载下断裂的试件变形严重,如图5(b)所示。由此得出:在静态加载下,改性双基推进剂表现出粘弹性材料特点,其弹性模量随受力作用时间变化;而在高应变率下,由于动态载荷作用时间非常短,该材料表现出了明显的脆性,即粘性可忽略。

图5 动态加载与静态加载失效前后比较Fig.5 Comparison before and after failure under dynamic loading and static loading
实验结果中,所有Ⅱ型试件高应变率下的断裂形式都如图5(a)所示:预制裂纹首先倾斜向中线方向传播(此时为Ⅰ-Ⅱ混合型裂纹),裂纹传播到试件的中线处后,则开始沿轴线传播(此时为I型裂纹),以后裂纹的传播方向不再发生变化。但实验应变率需控制在1 500 s-1以下,因为超过这个值试件会碎成多片,这说明其受力状态发生了改变,不能按照本文实验方法中所提出的假设进行分析。
图6为采用假设(2)所提出的紧密剪切试件剪切面应力、应变和应变率计算方法而得到的材料的应力应变关系随应变率变化的曲线图。
为了获得准静态与高应变率条件下实验结果的差异,图6中还加入了2 mm/min压缩速率下的实验结果曲线作为比较。从图5的实验结果和图6的应力-应变关系曲线可知:
(1)应力的最大值(裂纹初始扩展时的应力)随应变率的增加而显著增大,1 200 s-1条件下,失效应力强度是准静态条件下的近10倍;
(2)在高应变率范围内,失效应变(裂纹初始扩展时的应变值)随应变率的增大而减小;
(3)改性双基推进剂材料在高应变率下表现出明显的“脆化”现象。
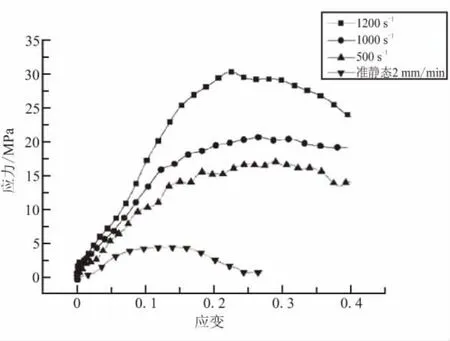
图6 应力应变关系随应变率变化的曲线Fig.6 Curve of the stress and strain relationship change with strain rate
3 断裂韧性及断裂能
根据动态力学应变与受力之间的关系[8],可计算得到试件两端的受力状态:
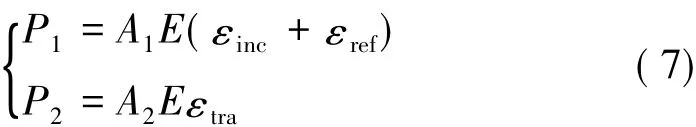
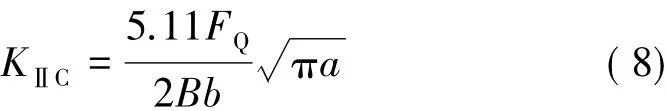
式中 FQ为试件受到的最大动态加载力;a、b和B如图2所示。
依据前文假设对材料的Ⅱ型断裂韧性进行计算。这样就用实验的方法得到了改性双基推进剂在应变率为3 000 s-1条件下的Ⅱ型断裂韧性 KⅡC=4.55 MPa·m1/2。
根据热力学第一定律,在SHPB实验设备中应力波能量的耗散可由ΔW通过式(9)表示[9]:
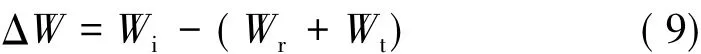
其中,Wi、Wr和Wt分别为入射波、反射波和透射波中的能量。可通过下面方法求得:式中 A1、A2分别为试件两端与杆的接触面积;P1、P2分别为试件与杆接触两个端面上的力;E为改性双基推进剂材料的松弛模量;εinc和εref为入射杆上应变片测得的应变,εtra为透射杆上应变片测得的应变。
由于试件设计时保证了A1=A2,因此试件两端的受力状态与应力状态相同,从而保证试件在加载过程中处于动力平衡状态。这样可将准静态下Ⅱ型断裂韧性的求取方法应用到高应变率下。由此,该试件的II型断裂韧性可通过式(8)[4]求出:
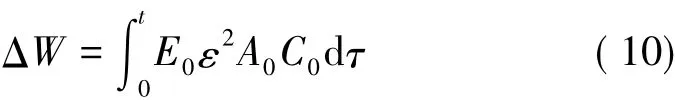
式中 E0、A0、C0为SHPB设备中杆的弹性模量、横截面积、应力波在杆中的传播速度;ε为应力波引起的时间解析应变。
通过分析可知道,应力波能量的耗散主要有以下几个去向:(1)试件发生断裂产生新的表面所需能量;(2)试件平动(K平)与转动(K转)的动能;(3)试件发生塑性变形所需的塑性功;(4)设备中各处的摩擦所做的功。由于在整个实验过程中采取了润滑措施,故可忽略摩擦损耗。在该材料断裂实验中,由于不同应变率下裂纹尖端的塑性区域大小不同,用实验的方法很难将塑性功和产生新表面所需的能量区分开。所以,计算时按照整体来考虑,这样就可将热力学第一定律简化为以下表达式:
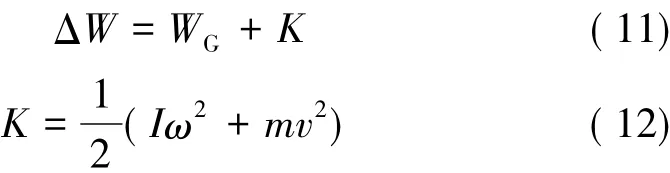
式中 WG为塑性功和产生新表面所需的能量的总和;K为试件平动与转动的动能。
图7(a)撞击时刻代表应力波开始作用在试件上,图7(b)是1/120 s时试件2个碎片分布照片。经过测量可得到试件断裂后所形成的两部分(如图7(b)中1、2 所示)的质量分别为 1.12 g 和 1.32 g,试件断裂形成2个碎片的飞行速度和转动速度分别为9.6 m/s和40 π/s。由实验获得的杆中的应力波和试件断裂产生的新的表面面积、转速、平动速度来计算得出材料的动态断裂能,各部分能量参数如表1所示。故材料的平均断裂能:
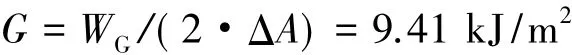

图7 实验过程中不同时刻试件位置Fig.7 Specimen′s position at different time during process of the experiment
平均断裂能G实际包含的是Ⅰ-Ⅱ混合型裂纹以及Ⅰ型裂纹的断裂能。断裂韧性KⅡC为Ⅱ型断裂韧性,故断裂能与断裂韧性之间的相关性不能使用GⅡ=/E来判断,而应使用包含有贡献因子的 G=为贡献因子)[10]进行验证,但改性双基推进剂材料贡献因子的分配和裂纹开裂形式之间的关系需要进一步研究。

表1 各部分能量参数Table 1 Each part of the energy parameter
4 结论
(1)改性双基推进剂紧密剪切试件裂纹扩展前受力主要为剪切力,满足了Ⅱ型断裂力学行为研究的边界条件。裂纹开始扩展时为Ⅰ-Ⅱ型混合裂纹;当传播到试件中心线位置时,裂纹路径开始沿试件中心线传播,此时该断裂变为I型断裂,即若试件足够大,裂纹会一直沿着Ⅰ型断裂方向进行扩展。
(2)紧密剪切试件高应变率条件下的实验研究应将应变率控制在1 500 s-1以下。低于这个值,试件预制裂纹扩展前受到的应力以剪切应力为主,失效形式为单裂纹扩展,求得的断裂韧性为Ⅱ型断裂韧性;高于该值,试件碎成多片,受力状态发生改变,不再适用于Ⅱ型断裂行为的研究。
(3)研究使用实验的方法,获得了改性双基推进剂材料在1 000 s-1应变率下的II型断裂韧性和平均断裂能2个主要断裂力学性能参数,并理论验证了这2个力学参数的准确性,从而反证了使用该实验方法获取粘弹性材料II型断裂参数的可行性。
[1]孟红磊,周长省,鞠玉涛.改性双基推进剂装药结构完整性数值仿真方法研究[D].南京:南京理工大学,2011.
[2]王蓬勃,王政时,鞠玉涛,等.双基推进剂高应变率本构模型的实验研究[J].固体火箭技术,2012,35(1).
[3]李兆民.端面燃烧固体火箭发动机的爆炸问题研究[J].推进技术,1989(6).
[4]Watkins J.Fracture toughness test for soil-cement samples in mode II[J].International Journal of Fracture,1983,22(3):135-138.
[5]Golewski G L,Golewski P,Sadowski T.Numerical modelling crack propagation under mode II fracture in plain[J].Computational Materials Science,2012,62:75-78.
[6]Vera E Petrova,Liviu Marsavina,Tomasz Sadowski.Revisit of compact mode II crack specimen analysis and fracture interpretation[J].Theoretical and Applied Fracture Mechanics,2012,59(1):41-48.
[7]Georges Challita,Ramzi Othman.Finite-element analysis of SHPB tests on double-lap adhesive joints[J].International Journal of Adhesion & Adhesive,2010,30(4):236-244.
[8]Dai F,Xia K,Zheng H,et al.Determination of dynamic rock mode-I fracture parameters using cracked chevron notched semi-circular bend specimen[J].Engineering Fracture Mechanics,2011,78(15):2633-2644.
[9]Chen R,Xia K,Dai F,et al.Determination of dynamic fracture parameters using a semi-circular bend technique in split Hopkinson pressure bar testing[J].Engineering Fracture Mechanics,2009,76(9):1268-1276.
[10]Brian Lawn.Fracture of brittle solids[M].United Kingdom:Cambridge University Press & Higher Education Press,2009.
(编辑:刘红利)
Fracture mechanics behavior of modified double-base propellant in modeⅡand high strain rate
ZHAO Chao,ZHENG Jian,JU Yu-tao,ZHANG Jun-fa,WANG Wen-qiang
(School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)
Using compact shear specimen,the fracture energy,fracture toughness and crack propagation path of modified double-base propellant under a series of high strain rates were studied.Experiment was conducted with split Hopkinson pressure bar,universal material test machine and high-speed digital photographic equipments.The results show that modified double-base propellant materials exhibit obvious viscoelasticity under quasi-static conditions,but brittleness under high strain rates.At last,compact shear specimen’s mechanical parameters like the rules of stress-strain relationship and crack propagation path under different strain rates,and the fracture energy,fracture toughness in 1 000 s-1are obtained through analysis and calculation.
modified double-base propellant;compact shear specimen;high strain rate;fracture energy;dynamic fracture toughness;crack propagation path
V435+.21
A
1006-2793(2014)04-0500-05
10.7673/j.issn.1006-2793.2014.04.013
2013-03-18;
2014-05-07。
赵超(1990—),男,硕士生,研究方向为固体火箭发动机装药断裂力学。E-mail:zhaochao203@163.com

