BPNN-HDMR非线性近似模型方法及应用*

李伟平，窦现东，王振兴，柳 超

( 湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082)

工程优化问题中，对于基于真实模型的嵌套优化，每次计算目标函数值都要调用费时的仿真计算模型，其计算代价不可小视.而利用近似模型可以有效地解决这一问题[1]，即通过对近似模型的求优近似得到真实模型的优化值.

目前广泛应用的一些近似方法，如响应面法、Kriging插值、人工神经网络等，在处理较低维问题时有很好的效果.而对于工程中复杂的高维非线性模型，随着维数和非线性程度的增加，构造近似模型所需的样本点数量和计算花费呈指数增长，使解决此类问题的计算效率大大降低[2].针对这一问题，Sobol证明了可积函数可以分解为不同维数函数的叠加理论[3].该理论表明，对于任意一个可以积分的函数，在其积分空间内存在唯一的、可以扩展的高维模型(High Dimensional Model Representation，HDMR).这一模型是精确的，有确定的阶数，并包含一个层级结构.高维模型可以将计算时间随非线性程度和维数增加按指数增长的隐函数，转化为可以忽略高阶耦合项的多项式函数，并揭示了每个设计变量对近似函数的贡献量，大大减少了计算时间.同时反映了输入变量之间固有的线性或非线性关系及其相关性，在近似高维非线性问题时非常有效.由此，一系列不同特性的高维模型开始发展起来，被研究和应用于不同的领域.其中，Shan等提出了基于径向基的高维模型(RBF-HDMR)[4],汤龙等提出了基于Kriging的高维模型(Kriging-HDMR)[5].

本文采用误差反向传播神经网络(Back Propagation Neural Network,BPNN)与中心切面高维模型(Cut-HDMR[6])方法相结合的BPNN-HDMR.BP神经网络是一种多层前馈型神经网络，其神经元的传递是S型函数，它可以实现从输入到输出的任意非线性映射.对于非线性问题，在精度表达上具有一定优势.Cut-HDMR方法是用过指定点的特定的直线、平面和超平面上的信息来建立模型，计算效率高，方便易行.

1 高维模型(HDMR)基本理论

设待求问题的设计变量可行域为An(n维实数空间)，那么多元函数f(x)∈R与输入变量x∈An之间的映射关系可以用HDMR[6-7]来表示为：

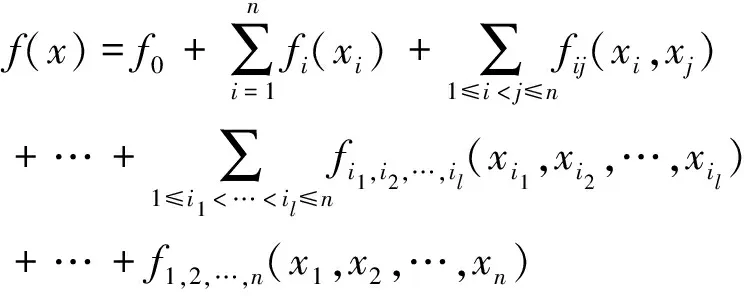
(1)

其中f0为函数在中心点的函数值，后面依次为不同阶耦合项对近似函数的贡献量.

为了方便计算，本文引入Cut-HDMR.与其他类型的高维模型相比，Cut-HDMR用少量简单的算术运算来表达计算花费高昂的真实模型，并达到了其他类型高维模型相似的精度，计算效率高.Cut-HDMR展开式的各分项表达请参考文献[6].

2 BPNN-HDMR

2.1 BP神经网络

BP网络是一种多层前馈型神经网络，它由一个输入层、一个输出层和至少一层隐含层组成[8].该网络的主要特点是信号向前传递，误差反向传播.在前向传递中，输入信号从输入层经隐含层逐层处理，直至输出层.每一层的神经元状态只影响下一层神经元状态.如果输出层得不到期望输出，则转入反向传播，根据预测误差调整网络权值和阈值，从而使BP神经网络预测输出不断逼近期望输出.因此，BP网络可以看作是解决函数逼近的工具.

本文中，隐层神经元的传递函数采用双曲正切S型函数h，它类似于一个平滑的阶梯函数：

h(x)=(ex-e-x)/(ex+e-x)

(2)

(3)

假设wi(k)为W(k)中的任意元素.调整wi(k)对误差Ek的影响直接取决于偏导数(∂Ek)/[∂wi(k)].BP算法的作用在于如何评价(∂Ek)/[∂wi(k)].详细内容可参考文献[9].这样，wi(k)就向着减小误差Ek的方向调整：

wi(k+1)=wi(k)-μ(∂Ek)/[∂wi(k)]，

∀wi(k)∈W(k)

(4)

其中μ为常量，是指定的更新率.可以看出，如果μ足够小时，则：

(5)

其中假设Ek>0.由式(5)可知，对于同样的输入参数x1,x2,…,xk，更新后的神经网络的输出更接近于真实函数输出值.

Hecht-Nielsen[9]研究了分层神经网络近似非线性函数的能力.他在文献[9]中表明，在确定的条件下，对于任意ε>0，存在一个三层神经网络(包含一个输入层，一个输出层和一个非线性隐含层)可以在均方误差精确度ε范围内近似函数f.因此，BP神经网络可以应用于工程实际中的大多数情况.

2.2 BPNN-HDMR的构建

对大多数工程问题而言，非耦合项和低阶耦合项对响应函数影响较大.为此，BPNN-HDMR方法只考虑到一阶耦合项，表达式如下：

(6)

高维模型的一般构建流程[4-5]如下：

1)选取各设计变量中心位置的点x0=[x10,x20,…,xn0]作为中心点，计算得到f0.

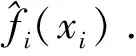
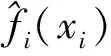
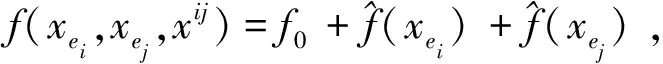
6)将上面构建的各阶BPNN近似函数代入式(6)就得到了高维模型近似响应函数.

本文高维模型构建时的精确度准则和收敛准则都是通过相对误差来定义的.精确度准则主要用于输入变量之间耦合性的识别，所允许的相对误差一般不超过10-4.由于本文方法具有较高精确度，所以本文针对测试函数收敛准则所允许的相对误差均取0.001；而对于工程问题，考虑到计算效率和一般工程要求的5%的近似精度，设置的相对误差均取0.01.通过以上设置，在样本点数一定时，由于本文方法将BP神经网络的非线性函数逼近能力与高维模型的层级结构理论相结合，所以本文近似模型方法在近似非线性问题时较传统方法具有更高的精度，建模效率也有所提高.

3 数值算例

3.1 评价指标

为了测试近似模型近似效果，采用3种比较常用的评价指标，R2(Rsquare),相对平均绝对误差(relative average absolute error,RAAE)和相对最大绝对误差(relative maximum absolute error,RMAE).这些指标反映了BPNN-HDMR在新样本点上的预测能力,其具体表达式请参考文献[4].其中，R2是从整体上反映近似模型的精度，其值越接近1越好；RAAE也是从整体上反映近似模型的精度，其值越小越好；RMAE是一个局部指标，描述了设计空间中某个局部区域的误差，其值越小越好.

3.2 函数算例

首先选择一个高维非线性测试函数：

xi∈[0,1]

(7)

采用相同数量的训练样本点(计算费用相同)，分别采用BPNN，BPNN-HDMR和Kriging 3种方法进行建模并比较它们的精度，计算结果如表1所示(表中数据是计算100次的平均值).

表1 BPNN，BPNN-HDMR和Kriging方法比较

分析表中数据，对于同一测试函数，3种近似方法中，BPNN-HDMR方法的R2值最接近1，RAAE和RMAE也都最小.由对比可知，对于高维非线性问题，基于同样数量的一组训练样本，采用BPNN-HDMR方法得到的近似模型精度更高.

其次，增加高维非线性测试函数式(7)的维数

0≤xi≤1

(8)

来测试BPNN-HDMR方法的效率.式(8)中，维数d分别取d=10,30,50等不同值，假设每一维的训练样本点数为9(经测试，基本可以满足精度要求)，表2中列出了各阶HDMR计算费用的比较.

表2 各阶HDMR建模费用的比较

4 工程应用

为了验证BPNN-HDMR在处理工程实际问题时的可行性，本文以某矿用自卸车全驾驶室式翻车保护装置(ROPS)的优化设计为例.根据标准ISO 3471：2008[13]对ROPS进行非线性有限元分析，确保ROPS满足标准ISO 3164:1992[14].通过仿真分析得到ROPS的变形量，为进一步优化打下基础.安全驾驶室ROPS的有限元模型如图1所示.

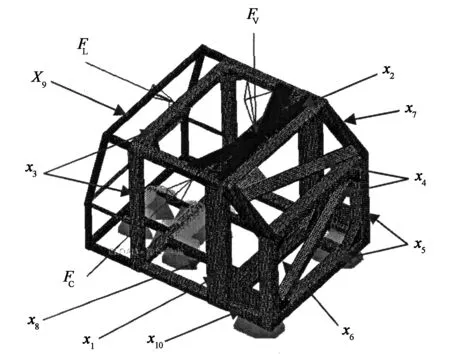
图1 ROPS加载分析模型

ROPS框架采用壳单元模拟，焊接使用刚性壳单元模拟为一个载荷变换器[15].焊接连接处网格局部加密，计算时假设焊缝与母材材料特性相同(实际中焊缝一般不先破坏).单元大小设定为20 mm，其中四边形单元54 951个，三角形单元1 389个，单元类型分别为S4R和S3R.本文ROPS材料为进口钢板A710，屈服极限为690 MPa，断裂极限为792 MPa，材料模型选择金属塑性材料模型，定义材料的应力应变曲线.依据标准ISO 3471：2008进行载荷和约束的施加.其中，约束ROPS底部与车架连接处3个平动方向的自由度(UX，UY，UZ)，FC为侧向力加载，FV为垂向力加载，FL为纵向力加载.标准挠曲极限量(Deflection-limiting volume ,DLV)与ROPS的侧向间距为200 mm，垂向间距为110 mm，纵向间距为320 mm.分析时考虑几何非线性和材料非线性.

4.1 优化变量的选取

本文优化的ROPS主要由一些不同厚度的矩形管和加强筋焊接而成.考虑对称性和加工可行性，对称的选取ROPS不同部位的矩形管厚度作为设计变量.各设计变量选取见图1，取值范围如表3所示．

表3 各优化变量取值范围

4.2 目标函数的建立

通过非线性有限元分析可知，由于要考虑ROPS侧向吸能问题，ROPS侧向变形最接近DLV，因此侧向变形为危险工况.根据企业要求，本文选取侧向变形作为一个优化目标，以垂向和纵向变形为约束.因此以ROPS侧向变形最小和ROPS质量最小建立多目标优化问题，ROPS的多目标优化模型可以描述为：

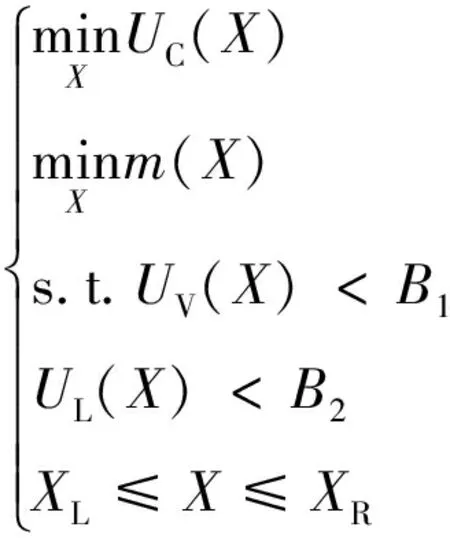
(9)

式(9)中UC为ROPS的侧向变形量；UV为ROPS的垂直变形量；UL为ROPS的纵向变形量；B1，B2分别为ROPS垂向和纵向的最大允许变形量；m为ROPS的总质量.

4.3 近似模型的构建

本文采用BPNN-HDMR构建ROPS变形量和质量响应近似模型.对每个设计变量在其取值范围内等间距取点，取点数量根据构建近似模型时是否达到预先设定的精度决定，通过ABAQUS计算获得样本点处的真实响应值.首先构建一阶项，然后进行精度判断.在设计变量空间，采用拉丁超立方实验设计方法，选择10个采样点.分别对真实模型和近似模型进行计算，并计算两者的相对误差.如果相对误差满足给定精度要求(设定为5%)，则构建近似模型成功，若精度不满足要求，则继续构建高阶项.

通过计算，本文所求近似模型只需计算到一阶项，就可以得到比较精确的近似结果，可以省略高阶耦合项.构建过程中只需56个样本点即得到满足工程要求的近似模型.

为了客观、全面地反映所建近似模型在设计域内的精确程度，在设计域内采用拉丁超立方实验设计方法随机生成10个测试样本点，用它们分别对BPNN，BPNN-HDMR和Kriging模型进行精度测试，并以侧向变形响应精度为例，测试结果如表4所示.

表4 采用BPNN，BPNN-HDMR和Kriging方法所得侧向变形近似模型的比较

由表4中数据可知，BPNN-HDMR解决此类工程问题具有高效准确的优点.同时，可以看出BPNN和Kriging方法在构建高维非线性有限元模型时的局限性，本文需要增加采样点数量才能用这两种方法获得比较精确的近似模型，这样就增加了真实有限元模型的计算次数，而真实非线性有限元模型一次计算要数小时，导致计算花费大大增加.

4.4 优化过程及结果分析

本文采用基于Pareto概念的多目标优化遗传算法，该方法是求解多目标问题非劣最优解的有效途径之一[16].在基于Pareto最优概念的遗传算法中，NSGA-Ⅱ[17-18]是最有效的.因此，本文采用NSGA-Ⅱ，在近似模型的基础上对ROPS进行多目标优化.

初始种群设为100，最大迭代次数设为200，交叉概率0.9，变异概率0.1.收敛规则为：达到最大迭代次数作为终止条件.得到Pareto最优解集如图2所示．

图2中星号表示多目标优化非劣解.在优化解集中取有代表性的10组解，多目标优化的Pareto最优解集见表5.ROPS优化前侧向变形和质量如表6所示.对比表6与表5中第4组和第6组数据可以看出，在质量相当的情况下，优化后的侧向变形大约减小了26.7 mm,在侧向变形相当的情况下，优化后的质量大约减小了75.1 kg.因此，通过多目标优化，ROPS的质量和变形情况明显改善.同时，根据得到的Pareto最优解集，可以根据设计者经验和需求，高效率地实现ROPS各矩形管厚度的选取，以满足不同性能需要.

把优化结果代入有限元计算模型验证，计算结果如表7所示.

由ABAQUS计算验证可知，所选优化解都符合标准ISO 3164:1992的要求.这也证明了本文所提方法在工程优化实际应用中的可行性和有效性.同时，由于模型简化掉了一些蒙皮和附属部件，以及真实情况下车架也有一部分吸能作用，所以本文的分析结果是偏向安全的.

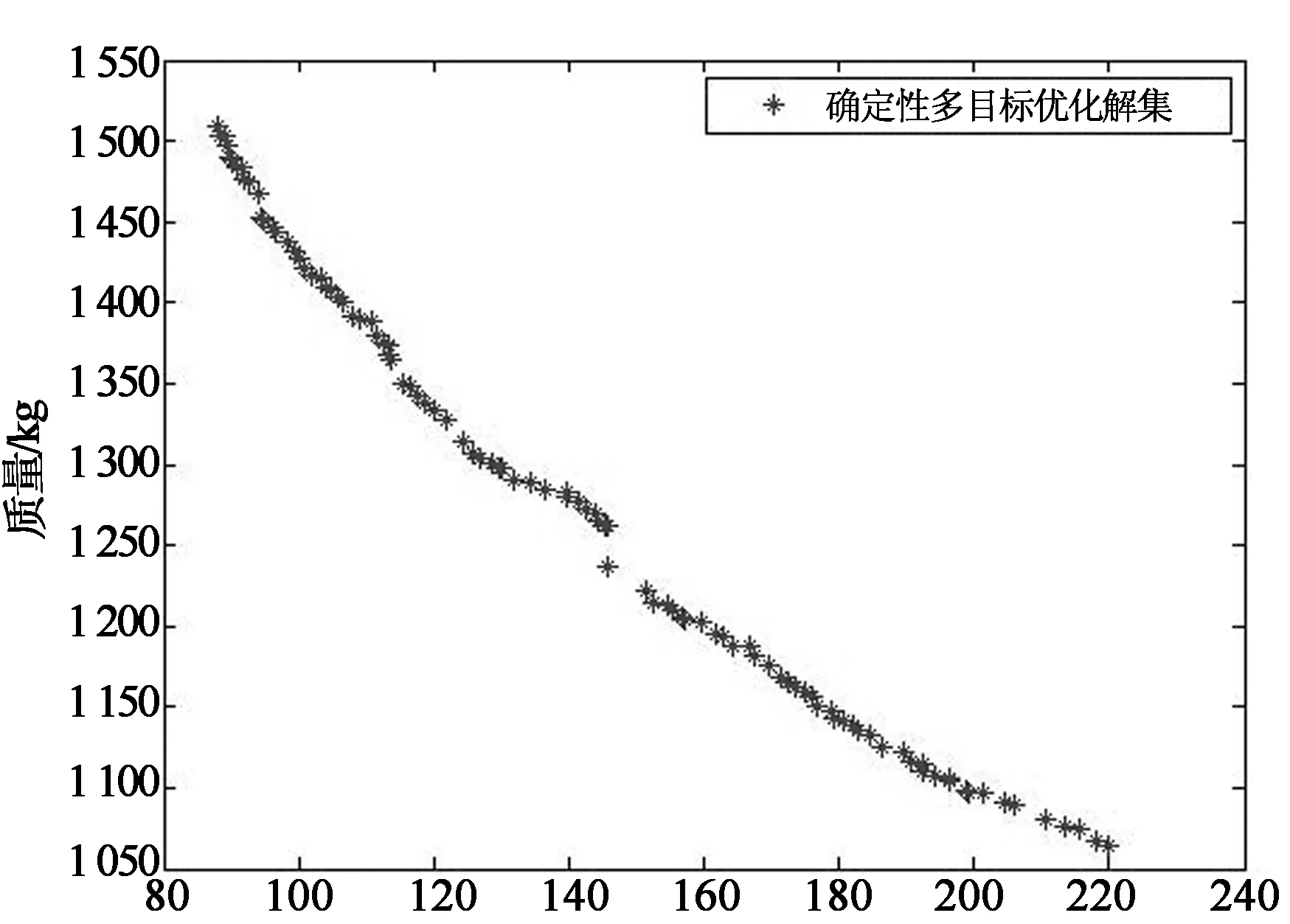
侧向变形/mm

表5 双目标优化的Pareto最优解

表6 ROPS侧向变形优化前数据

表7 优化后的响应值ABAQUS计算验证

5 结 论

本文提出的BPNN-HDMR建模方法，很好地利用了BP神经网络的非线性函数逼近能力与高维模型的层级结构理论，并能够反映输入变量之间固有的线性关系和耦合性.尤其对于高维问题，它可以将构造模型计算花费由维数的指数级增长降解为多项式级，有效地解决了高维建模问题，且与传统算法相比，具有更高的精度.通过数值算例和工程优化问题的对比，验证了BPNN-HDMR近似方法的精度和效率.另外，该算法对于高度非线性问题精确的数学建模还需进一步发展和完善，BP神经网络的计算效率也有待进一步提高.同时，本文所采用的结构分析与优化方法在工程领域的其他方面也可以广泛应用，具有一定的理论和工程实际意义.

[1]穆雪峰.多学科设计优化代理模型技术的研究和应用[D].南京：南京航空航天大学航空宇航学院，2004.

MU Xue-feng.The research and application of multidiscipline design optimization surrogate model technology[D].Nanjing: College of Aerospace Engineering,Nanjing University of Aeronautics and Astronautics,2004.(In Chinese)

[2]赵子衡，韩旭，姜潮.基于近似模型的非线性区间数优化方法及其应用[J].计算力学学报，2010，27(3):451-456.

ZHAO Zi-heng,HAN Xu,JIANG Chao.Approximation model based nonlinear interval number optimization method and its application [J].Chinese Journal of Computational Mechanics,2010,27(3):451-456.(In Chinese)

[3]SOBOL I M.Sensitivity estimates for nonlinear mathematical models [J].Mathematical Modeling & Computational Experiment,1993,1(4): 407-414.

[4]SHAN Song-qing,WANG G Gary.Metamodeling for high dimensional simulation-based design problems[J].Journal of Mechanical Design,2010,132:051009.

[5]汤龙，李光耀，王琥.Kriging-HDMR非线性近似模型方法[J].力学学报，2011，43(4):780-784.

TANG Long,LI Guang-yao,WANG Hu.Kriging-HDMR metamodeling technique for nonlinear problems [J].Chinese Journal of Theoretical and Applied Mechanics,2011,43(4):780-784.(In Chinese)

[6]RABITZ H,AL1S Ö F.General foundations of high-dimensional model representations[J].Journal of Mathematical Chemistry,1999,25(2/3):197-233.

[7]LI G,WANG S W,ROSENTHAL C,etal.High dimensional model representations generated from low dimensional data samples.I.Mp-Cut-HDMR[J].Journal of Mathematical Chemistry,2001,30(1): 1-30.

[8]CHEN Fu-chang .Back-propagation neural networks for nonlinear self tuning adaptive control[J].Control Systems Magazine,IEEE April,1990,10(3): 44-48.

[9]HECHT-NIELSEN R.Theory of the back-propagation neural network[C]//Proc IEEE 2002 Intl Conf Neural Networks.Califormia:International Toint Conference in Nemal Networks,2002.

[10]谢庆生，尹健，罗延科,等.机械工程中的神经网络方法[M].北京：机械工业出版社，2003: 39-51.

XIE Qing-sheng,YIN Jian,LUO Yan-ke,etal.Neural network method in mechanical engineering [M].Beijing:China Machine Press,2003:39-51.(In Chinese)

[11]曾喆昭，李仁发.高阶多通带滤波器优化设计研究[J].电子学报,2002,30(1):87-89.

ZENG Zhe-zhao,LI Ren-fa.Study on the optimum design of the high-order multi-band-pass filters [J].Acta Electronica Sinica,2002,30(1):87-89.(In Chinese)

[12]张德丰.MATLAB 神经网络应用设计[M].北京：机械工业出版社，2012:49-75.

ZHANG De-feng． MATLAB neural network application design [M].Beijing:China Machine Press,2012:49-75.(In Chinese)

[13]ISO 3471:2008 Earth-moving machinery-roll-over protective structures-laboratory tests and performance requirements[S].British: Standards Policy and Strategy Committee,2009.

[14]ISO 3164: 1992 Earth-moving machinery —Laboratory evaluation of roll-over and falling-object protective structures-specifications for deflection-limiting volume[S].British: The Authority of the Standards Board,1992．

[15]周传月.MSC.Fatigue疲劳分析应用与实例[M].北京:科学出版社，2005:86-91.

ZHOU Chuan-yue.Fatigue analysis of application and examples with MSC.Fatigue[M].Beijing:Science Press,2005:86-91.(In Chinese)

[16]谢涛，陈火旺，康立山.多目标优化的演化算法[J].计算机学报,2003,26(8):997-1003.

XIE Tao,CHEN Huo-wang,KANG Li-shan.Evolutionary algorithms of multi-objective optimization problems [J].Chinese Journal of Computers,2003,26(8):997-1003.(In Chinese)

[17]DEB K,PRATAP A,AGARWAL S,etal.A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II,Kan GAL Report No.200001[R].Kanpur: Indian Istitute of Technology,2000.

[18]李伟平,王世东,周兵,等.基于响应面法和NSGA-Ⅱ算法的麦弗逊悬架优化[J].湖南大学学报:自然科学版,2011,38(6):27-32.

LI Wei-ping,WANG Shi-dong,ZHOU Bin,etal.Macpherson suspension parameter optimization based on response surface method and NSGA-Ⅱ algorithm [J].Journal of Hunan University:Natural Sciences,2011,38(6):27-32.(In Chinese)