碳纤维板-混凝土界面黏结性能的试验研究与有限元分析*

尚守平，李知兵,2†，彭 晖

(1．湖南大学 土木工程学院，湖南 长沙 410082；2. 湖南工学院 建筑工程与艺术学院，湖南 衡阳 421002； 3. 长沙理工大学 土木与建筑学院，湖南 长沙 410004)

近年来外贴碳纤维板加固在建筑及桥梁结构加固补强中应用广泛，在碳纤维板与混凝土间传递应力的界面黏结，对加固结构受力性能起着至关重要的作用.为精确预测加固结构的力学行为，需要深入把握黏结界面的受力行为.因此研究人员对加固结构的受力性能和力学行为开展了大量研究[1-6]，设计了各种界面黏结性能的试验测试装置并通过试验考察了界面受剪行为；推导了碳纤维板加固钢筋混凝土受弯构件界面应力的计算公式；也针对黏结界面的特点建立了平面有限元模型分析界面剪应力-滑移关系.已有的单剪试验方法操作较繁琐，试验结果受试验设备和试件形状影响较大；已完成的有限元分析通常忽略黏结层的受剪滑移，直接在界面将两种材料节点耦合，或将整个结构简化成平面进行分析[7-9]；现有的剪应力-滑移计算理论模型较多，考虑的参数较片面且不一致.鉴于此，本文参考Yun等人[10]的试验设计，实施了双面粘贴碳纤维板的混凝土棱柱体组合试件的受剪试验；研究了界面受剪条件下黏结应力变化规律；得到了黏结-滑移曲线，定义了适用黏结界面受力状态的弹簧单元组，建立了相应的三维有限元模型，并将分析结果和试验结果进行了对比分析；基于已有的黏结-滑移本构关系进行了本文试验所得到的黏结-滑移曲线值拟合，比较了不同本构模型与试验结果的吻合程度.

1 碳纤维板-混凝土界面双剪试验

1.1 试件设计

本文采用的试验形式为界面双剪试验.试件由2个尺寸为150 mm×150 mm×300 mm的混凝土棱柱体对接组成；在棱柱体的2个相对侧面分别粘贴了由西卡公司生产的，截面尺寸为50 mm×1.2 mm的Sika-S512型碳纤维板；棱柱体端部中心埋设有便于试验机夹持的螺纹钢拉杆；为防止试件在加工和试验过程中碳纤维板出现偏心受力，并保证试验过程中2个混凝土棱柱体只出现相对竖向位移，特进行了以下处理：在2个混凝土棱柱体端部光面上各用结构胶黏有一块同棱柱体截面大小的10 mm厚方形钢板，钢板4个对应角点分别垂直焊有同尺寸钢杆，再通过直径略大于钢杆的铜质套筒连接对应钢杆实现2个棱柱体的准确对中.试件如图1所示.

图1 试件设计

4个试件所使用的混凝土标号为C30，实测28 d立方体试块抗压强度为31.5 MPa, 30.5 MPa, 32.4 MPa, 32.5 MPa.主要材料力学性能见表1.为控制界面剥离现象出现的位置，B区粘贴长度B1B2为200 mm，大于Chen和Teng公式[3]计算的有效黏结长度Le=190.1 mm，而A区粘贴长度小于B端，则理论上A区首先出现开裂情况；为避免界面出现剥离时引发棱柱体边缘混凝土撕裂，对整个剥离行为产生影响，特在粘贴区之前设置一段非粘贴区A1B1.同时设计制作了A区不同粘贴区长度和相同胶层厚度的4组试件进行对比试验，试件具体参数见表2.

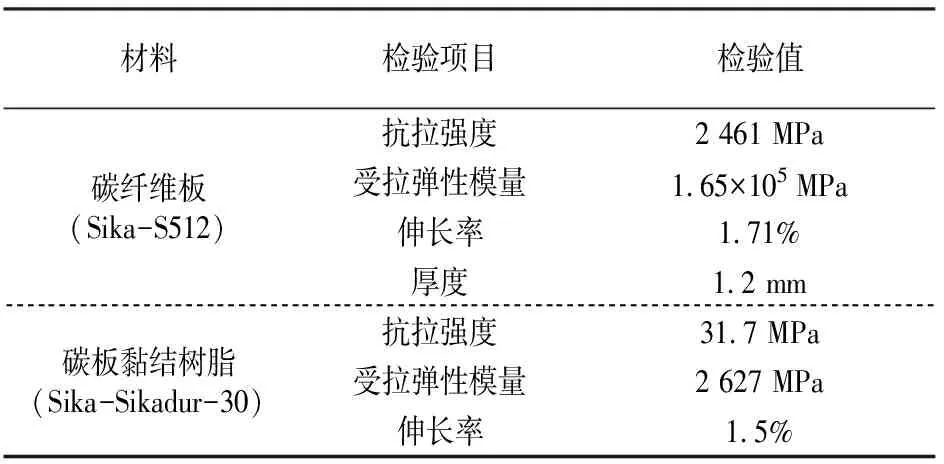
表1 试件材料力学性能

表2 试件粘贴区长度设置

1.2 测点布置及试验加载过程

界面的黏结应力一般由碳板粘贴区部分的应变间接反映[11-13].因设置粘贴长度相对较小的A区为实验区，故在试验过程中主要观测A区的碳纤维板应力变化和界面的剥离破坏现象.主要通过在A区碳纤维板上连续布置的5 mm×3 mm规格的电阻应变片采集，试件CF-15-1/15-2粘贴区碳纤维板应变片具体布置如图2所示.界面的滑移量一般也可以通过碳板应变反映，但是为了准确测得滑移量，本实验中采用在靠近A2端2个应变片之间布置由钢铁研究总院生产的电子引伸计来测量碳板与混凝土之间的滑移量.

为了得到碳纤维板与混凝土界面之间的裂缝出现时间、发展规律以及破坏形式、破坏特征等，试验严格采用分级加载制度.首先预加载2 kN，预载2～3次，检查试件2片碳纤维板应变是否正常.从2 kN开始按3 kN每级的分级加载至理论极限荷载的一半，再以2 kN每级加载捕捉界面开裂荷载和极限荷载.在每级加载完毕之后，需等待5～8 min，待应变值稳定下来再记录应变值.试验加载过程采用美国MTS公司810多功能材性试验机，每级荷载值可通过配套计算机软件精确控制(如图3所示).

图2 试件CF-15-1/15-2粘贴区碳纤维板应变片测点布置(单位：mm)

图3 试验加载装置

1.3 试验结果及分析

在试验中可以观察到界面裂缝首先在A区A1点附近出现，试件CF-10-1和CF-10-2(粘贴长度为100 mm)分别在加载至26 kN和28 kN时观察到黏结界面裂缝，而CF-15-1和CF-15-2(粘贴长度为150 mm)的界面开裂荷载分别为32 kN和36 kN.随着荷载的继续增加，界面裂缝迅速向板端发展.最终破坏状态为“啪”的声响伴随黏结胶层和混凝土界面的完全剥离，如图4所示，剥离的碳纤维板在A1点附近会附带少量混凝土下来，因破坏过程突然，板端甚至会有部分碳纤维从碳板上被撕扯下来.实测粘贴区长为100 mm的试件极限剥离承载力为33.2 kN和37.1 kN，粘贴区长为150 mm的试件的极限剥离承载力为44.5 kN和46.4 kN.这里开裂荷载约为极限抗力的24%，亦即，当拉伸应力超过碳纤维板强度的24%时，碳板已开始从混凝土表面剥离，如果没有锚具，预应力将不能有效地传递到混凝土构件上.

(a) 端部界面剥离

(b)界面破坏后碳纤维被撕扯下来

图5描绘了试件CF-10-1/10-2粘贴区碳纤维板测点的荷载-应变曲线.由图可见，当荷载值较小时，CFRP板、黏结胶层和混凝土共同承受荷载作用，此时各位置应变同步增加.随着荷载的加大，混凝土表面拉应力、CFRP板与混凝土之间的黏结应力也不断增大，此时不同位置的应变发展呈现不同的规律：A粘贴区近A2点碳纤维板自由端应变较小，随荷载增加没有明显变化；近A1点碳纤维板应变和粘贴区中部应变则随荷载增大呈线性变化.当荷载达到一定值时，界面之间应力分布开始变得不均匀而在薄弱部位发生开裂或损伤，此时界面应力重分布.从图上也可观察到近A1点碳纤维板应变和粘贴区中部应变在加载过程中先后出现拐点，反映了界面裂缝从加载点向粘贴区中间扩展的现象，且拐点对应荷载值与试验观测到的开裂荷载很接近，同样的规律也在试件CF-15-1/15-2上得到反映.

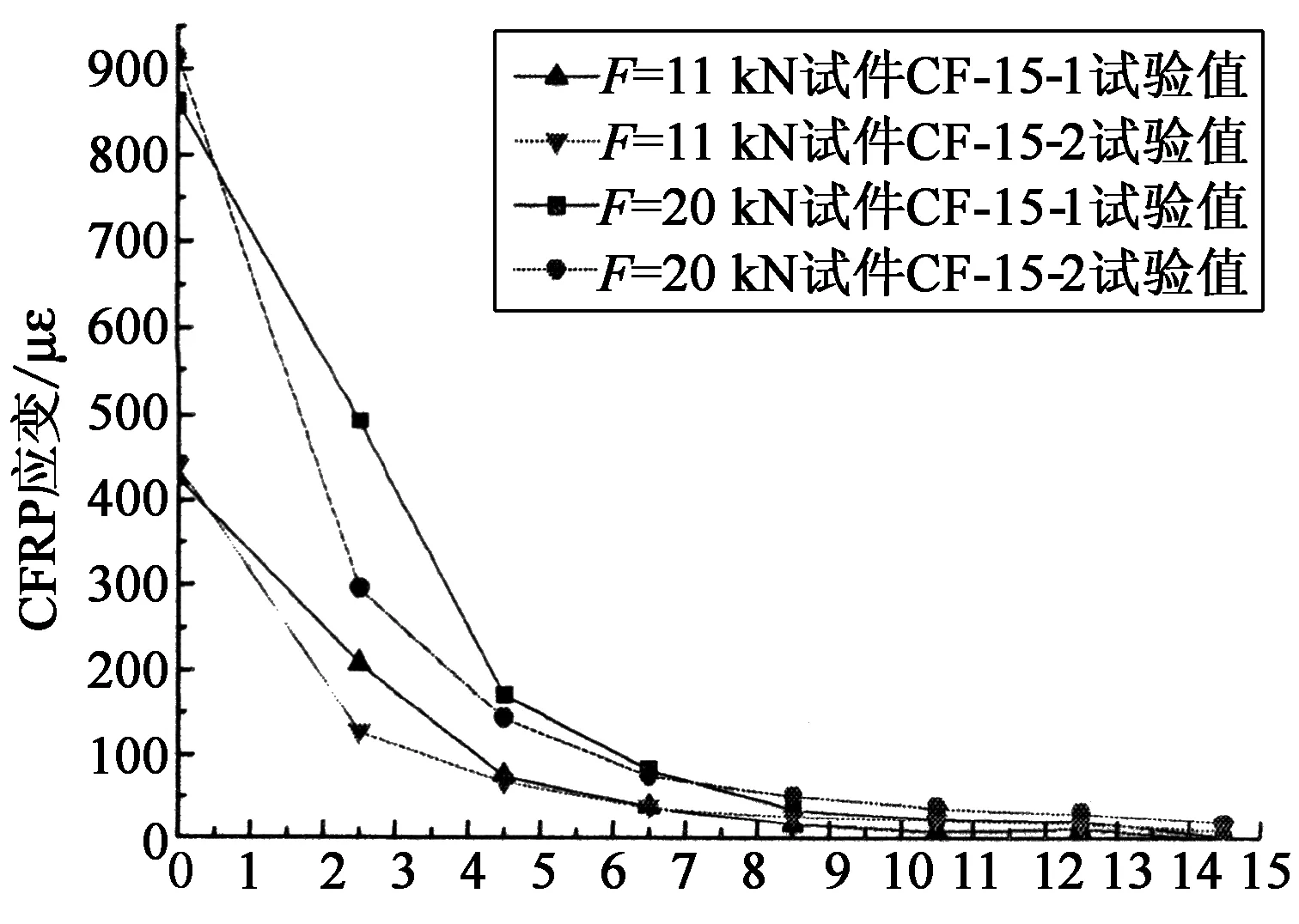
试件在25%和50%极限荷载作用下，沿板长方向各测点的碳纤维板应变分布如图6和图7所示，试验中每个试件均采集了2面的碳纤维板应变值，经比较发现对应点的应变较一致，故将对应点应变值取均值以便与其他试件比较.

CFRP应变/με

测点与A1点距离/cm

测点与A1点距离/cm

由上图试验结果可看到：在界面开裂之前，不同粘贴区长度的试件在A粘贴区0～10 cm范围内碳板应变分布趋势较接近，沿板长方向大致呈指数衰减分布；而试件CF-15-1/15-2在A粘贴区10～15 cm的范围内碳板应变基本不随荷载变化，提供了一定的强度储备，故其开裂荷载和极限荷载更高.总体而言，在缺乏适当锚固的条件下，黏结树脂对于外贴碳纤维板能提供的黏结承载力较为有限，为充分发挥碳纤维板的高强性能，可考虑采用锚具对碳纤维板进行锚固.

2 有限元模型分析

2.1 CFRP-混凝土界面单元选取

CFRP与混凝土之间的受力机理复杂，已有的部分有限元模型为简化分析，未考虑界面的黏结滑移.这就使得准确模拟和分析界面黏结性能变得不可能.随着界面单元的引入，利用有限元分析CFRP与混凝土之间的受力机理变得可行[14-15].有限元分析中，CFRP-混凝土模型的建立目前较为合理的是使CFRP与混凝土共节点方式，为了反映CFRP-混凝土之间的黏结滑移关系，非线性2维界面单元被置入共用节点之中.非线性2维界面单元很多，应用较为广泛的包括弹簧单元、离散束单元、连续单元等.Ahmed Godat等[16]对这3种单元进行了数值模拟，发现3种界面单元都能够有效地模拟界面黏结滑移，但是存在一定的差异.

本文在已有的有限元模型基础上，考虑使用弹簧单元组连接混凝土和碳纤维板以模拟界面的受力.该弹簧单元组如图8所示，通过在混凝土棱柱体和碳纤维板模型对应节点之间设立法向和切向2个正交单向弹簧组成.

图8 正交弹簧组示意图

弹簧单元采用可以设置F(荷载)-D(变形)曲线来定义材料本构关系的COMBIN39单元，弹簧的自由度方向通过在实常数中设置单元的关键字选项KEYOPT(n)=x(n,x的设置参考ANSYS单元手册)来控制，如图9所示.

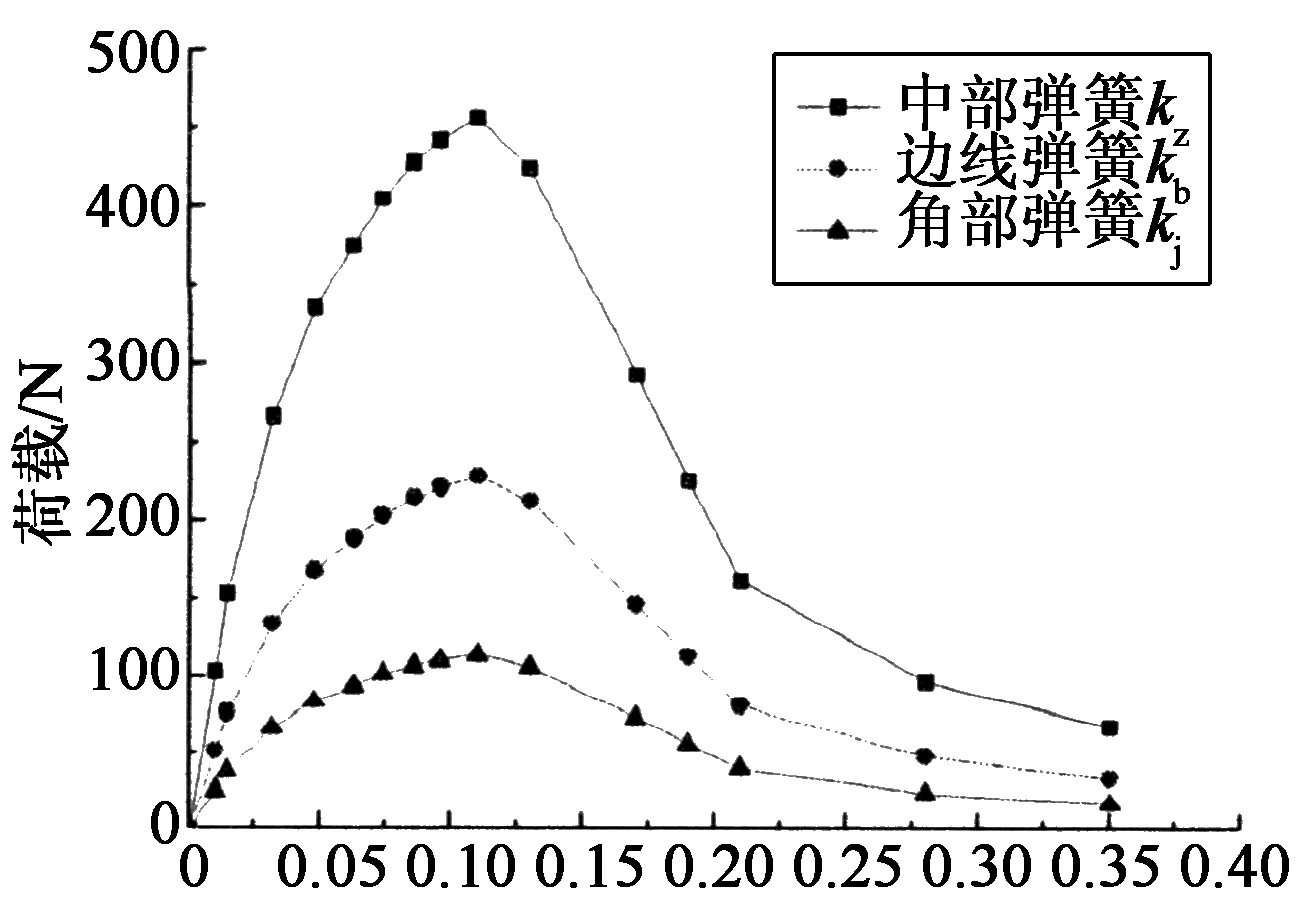
对于切线弹簧，每根弹簧单元的刚度表现为黏结-滑移关系的一阶导数，k=dF/dδ，又F=τ(δ)×A，τ(δ)为界面的黏结滑移关系模型，A为每个弹簧的作用面积．如图10所示每个弹簧的位置不同导致弹簧单元等效作用面积A不同，故所选取的界面有3种不同刚度，根据弹簧不同位置可以定义为角点弹簧kj, 边线弹簧kb, 中间弹簧kz，对于胶层作用面积分别为：Aj，Ab，Az，其中Aj=a×b/4，Ab=a×b/2，Az=a×b，式中，a,b分别表示胶层(同CFRP板)单元网格纵向尺寸和横向尺寸.界面弹簧单元的布置和作用面积如图10所示.

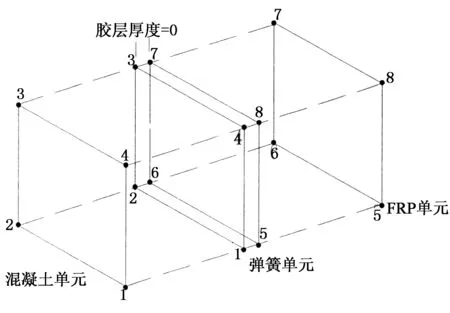
图9 CFRP-混凝土单元连接示意图

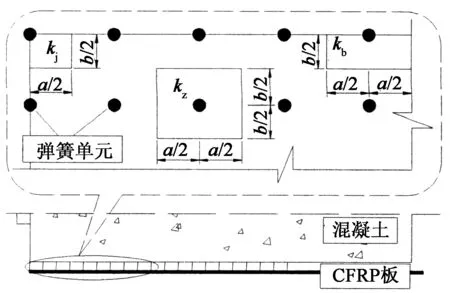
图10 界面弹簧单元布置

2.2 静载下的界面局部黏结-滑移关系

界面黏结滑移本构关系决定了FRP片材与混凝土之间的黏结行为，也是通过数值模拟分析界面黏结性能的基础．国内外众多研究人员也通过试验与理论研究构建了不同的黏结滑移本构模型，比较典型的有Popovics模型、双线性模型、三线性模型、陆新征精细有限元模型、T. Ueda[14]所建议模型等.然而由于不同模型存在尺寸效应，直接采用经典黏结滑移模型不能较好地与本试验结果吻合.尽管直接从双剪或单剪实验获得界面的黏结滑移曲线比较困难，但是大量的学者结合理论及实验得到了局部的黏结滑移本构关系，基于试验结果，不少学者以经典的黏结滑移本构关系为基础，对黏结滑移本构模型进行了修正，比如Nakaba[17]，Monti[18]以及Savioa[19]等以Popovics模型为基础得到了其试验的黏结滑移本构关系.本文以试验得到的局部黏结滑移本构关系为基础，通过分析拟合得到基于几种经典黏结滑移本构关系的数学模型.

局部黏结滑移关系对于确定界面的黏结性能的本构关系是尤为重要的一步.现有的获得界面黏结滑移曲线的一种方法是通过分析FRP的应变分布曲线得到τ-s关系. Dai等[20]在FRP-混凝土双剪试验中通过整合试验中的应变片数据结合以下公式(1)和(2)可以得到其黏结滑移本构模型.本文也采用 Dai等[20]在文章中提到的公式计算静力下局部黏结应力，并结合引伸计测得的相应滑移量，得到了本文试验的黏结滑移关系.

CFRP板上应变片间距是10 mm，局部的滑移量通过引伸计测出，并通过CFRP板应变分析验证.第i个应变片位置的滑移值为：

(1)

第i个应变片位置局部黏结应力为：

(2)

式中:si为第i个应变片位置处的CFRP板与混凝土之间的局部滑移量；Δx为应变片间距；ε0为黏结区自由端的应变片值；εj(j=1,i)为沿CFRP板长方向第j个应变片值；τi为第i个应变片位置处的CFRP板与混凝土之间的黏结应力；Ef和tf分别为CFRP板的弹性模量和厚度.通过分析试验结果，得到了碳纤维板-混凝土的局部黏结滑移曲线，并转换成有限元当中所采用的各切向弹簧的荷载-变形曲线如图11和图12所示.

滑移量/mm

滑移量/mm

在界面受剪分析中发现法向弹簧的刚度对碳板应变的分布大小几乎没有影响，弹簧单元更多地是模拟沿板长方向的滑移，故在计算中取其刚度值略大于切向弹簧的刚度即可.

2.3 试件有限元模型

基于上述工作，本文使用通用有限元软件ANSYS建立了试件的有限元模型(如图13所示).模型中根据试验类型和试件结构特点分别模拟了混凝土、钢拉杆、碳纤维板和环氧树脂胶层4种材料.考虑到界面剥离大多出现在胶层-混凝土界面，且会扯下薄层混凝土，所以混凝土单元采用可以模拟混凝土开裂的SOLID65单元；试件的Φ20螺杆采用双线性实体单元SOLID45模拟；碳纤维板采用具有大变形功能的SHELL63单元模拟.

图13 有限元模型

3 分析结果和试验值对比

在试验研究和有限元分析基础上，本文对25%和50%极限荷载下沿板长方向碳纤维板的应变分布的试验结果和分析结果分别进行了对比，如图14和图15所示.

测点与A的距离/cm

测点与A1的距离/cm

测点与A的距离/cm

测点与A1的距离/cm

由图14和图15可以看出，本文试验结果和有限元模型计算结果吻合较好，碳纤维板应变分布规律和应变值比较接近.试验值和计算值都反映了A粘贴区黏结层近A1点切向应力较大，从计算模型中也可以观察到界面裂缝首先在此端混凝土出现，而近A2点黏结层切向应力几乎为0.提取有限元分析结果：CF-10-1/10-2试件和CF-15-1/15-2试件的极限承载力分别为36.5 kN和46 kN，这与CF-10-1/10-2试件和CF-15-1/15-2试件的平均试验承载力35.2 kN和45.5 kN比较接近，进一步说明了试验得到的局部界面黏结滑移曲线关系符合本实验的黏结滑移本构关系.

4 黏结滑移本构模型比较

在前述工作基础上，本文根据试验得到的界面黏结滑移关系，拟合确定了Popovics模型、双曲线模型、T. Ueda模型等界面黏结滑移模型的相关系数，并将拟合结果与试验结果进行了比较.

4.1 Popovics模型

Popovics表达式如式(3)所示，Nakaba[17], Monti[18]以及Savioa[19]都应用该模型对碳纤维加固混凝土结构界面黏结滑移曲线进行过拟合，也均得到了与试验比较相近的结果.

τ=τmaxas/s0/[(a-1)+(s/s0)a].

(3)

式中：τ为黏结应力；τmax为最大黏结应力；s为局部滑移量；s0为最大黏结应力对应的滑移量；a为回归系数，通过本文试验结果拟合CF-10-1/10-2的a值为3.4，CF-15-1/15-2 的a值为3.42.

4.2 双曲线模型

典型的双曲线模型由上升段和下降段组成，故可分别用不同的函数表示.双曲线基本表达式为：

(4)

式中：a，b均为回归系数，本次试验拟合值为：CF-10-1/10-2试件的a=0.57,b=0.66 ,CF-15-1/15-2试件的a=0.621，b=0.676.

4.3 T.Ueda模型

T. Ueda[14]所建议的黏结滑移本构关如下：

τ=2BGf(e-Bs-e-2Bs).

(5)

其中，

B=0.846(Eftf)0.108(Ga/ta)0.833；

τmax=0.5BGf，s0=0.693/B；

Ga/ta=Gp·Gad/(Gptad+Gadtp)；

式中:A表示胶层单元作用面积；τ表示胶层的剪应力;s表示界面的滑移量;f(s)是s的函数；B表示材料性能常数;Gf表示界面破坏能；Gp和Gad分别表示碳板和胶层剪切模量；Ep和Ead分别表示碳板和胶层弹性模量；tp和tad分别表示碳板和胶层材料的厚度；Ga/ta为界面的刚度系数.

由于式(5)中考虑的影响界面黏结滑移的参数较多，而本课题组未进行大量的试验对影响界面黏结性能的参数进行分析，但是大量学者在进行界面黏结滑移分析时发现，胶层刚度对界面黏结滑移关系影响较大，而大多数黏结滑移本构关系未曾考虑胶层刚度对界面黏结性能的影响，尤其是在疲劳循环过程中胶层刚度对界面黏结性能影响最为显著，故在黏结滑移本构关系中引入胶层刚度参数更能够体现界面黏结性能的本质.这里简单地以公式(6)为基础，设定3个回归分析变量，具体表达式如下：

τ=c(e-as-e-bs).

(6)

式中：a,b,c为回归系数.回归分析得：CF-10-1/10-2试件的a=11.31，b=11.64，c=387.6，CF-15-1/15-2试件的a=11.67，b=11.98，c=432.9.

4.4 Dai and Ueda模型[20-21]

Dai和Ueda结合双曲线模型，从影响界面黏结性能的多重因素出发，提出了具体的黏结滑移本构关系，表达式如下：

(7)

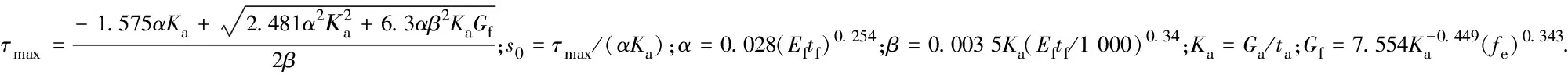
Dai和Ueda模型的上升段与双曲线模型完全相同，对于其下降段取β为回归系数，回归得到CF-10-1/10-2试件的β为6.757，CF-15-1/15-2试件的β为7.123 5.

比较Dai和Ueda模型和双曲线模型发现，Dai 和Ueda模型考虑了所有影响界面黏结性能的因素，Dai和Ueda在研究中发现界面胶层剪切刚度对界面黏结性能至关重要，相反FRP刚度对界面黏结性能影响不大，故在黏结滑移本构模型中考虑了界面胶层剪切刚度的影响.

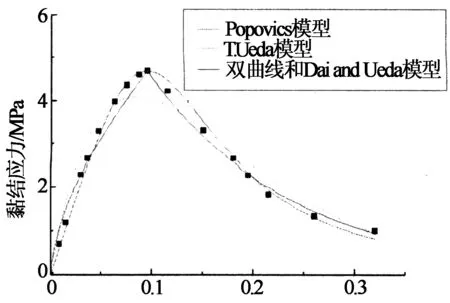
将以上几种回归分析曲线与试验得到的黏结滑移曲线展现在图16及图17中.

滑移量/mm

滑移量/mm

由图可知，Popovics模型和双曲线模型均与试验值吻合较好，T.Ueda模型与试验值相差较大，这是因为影响回归分析变量的因素很多，试验未能得到考虑多重因素影响下的回归分析值，因而拟合曲线差异较大.但是T.Ueda模型考虑了多重因素的影响，更能够体现界面黏结性能的复杂程度，故参考价值很大，在以后的试验中可以依据T.Ueda模型设置多重影响因素的大量试验，以期获得更加正确的黏结滑移本构数学模型.

5 结 论

根据本文试验与分析可以得到如下结论：

1)试验获得的黏结区域FRP应变数据表明：在界面开裂之前，不同粘贴区长度的试件在A粘贴区碳板应变分布趋势较接近，沿板长方向大致呈指数衰减分布；而试件CF-15-1/15-2在A粘贴区10～15 cm的范围内碳板应变基本不随荷载变化，提供了一定的强度储备，故其开裂荷载和极限承载力更高.当拉伸应力超过碳纤维板强度的24%时，碳板已开始从混凝土表面剥离，亦即，仅用胶粘贴碳板会过早剥落.为保证充分利用碳纤维板强度，应采用可靠锚具对碳纤维板进行锚固.

2)试验得到的局部黏结滑移关系与典型的黏结滑移曲线关系有相同的特征，基于几种典型的本构关系的数据回归分析拟合，得到了符合本试验的黏结滑移本构数学模型，Popovics模型、双曲线模型、Dai 和Ueda模型均与试验吻合较好，而T.Ueda模型差异较大.这些拟合的数学本构模型均能够运用到实际工程中.但Dai和Ueda模型及T.Ueda模型均考虑了所有界面组成材料的综合因素的影响，更能够反映界面黏结性能的真实性，故参考价值更高，如果能够建立考虑多重影响界面黏结性能因素的试验组，就能够拟合出基于这2种模型的准确模型.

[1] 邓军, 黄培彦. 预应力CFRP 板加固梁的界面应力分析[J].工程力学, 2009, 26(7):78-82.

DENG Jun, HUANG Pei-yan. Interfaical stress analysis of beams strengthened with a prestressed CFRP plate[J]. Engineering Mechanics, 2009, 26(7):78-88.(In Chinese)

[2] 陆新征, 滕锦光，叶列平，等. FRP加固混凝土梁受弯剥离破坏的有限元分析[J].工程力学，2006，23(6)：85-93.

LU Xin-zheng, TENG Jin-guang，YE Lie-ping,etal. Finite element analysis of intermediate crack-induced debonding in FRP strengthened RC beams[J]. Engineering Mechanics, 2006, 23(6):85-93. (In Chinese)

[3] 滕锦光, 陈建飞. FRP加固混凝土结构[M].北京: 中国建筑工业出版社, 2005:11-74.

TENG Jin-guang, CHEN Jian-fei. FRP strengthed RC structures[M]. Beijing: China Architecture & Building Press, 2005:11-74.(In Chinese)

[4] 姚谏, 滕锦光. FRP复合材料与混凝土的黏结强度试验研究[J]. 建筑结构学报, 2003, 24(5): 10-17.

YAO Jian,TENG Jin-guang. Experiment study on bond strength between FRP and concrete[J]. Journal of Building Structures, 2003, 24(5): 10-17. (In Chinese)

[5] 彭晖,尚守平,张建仁,等. 预应力碳纤维板加固T梁的试验与理论研究[J]. 公路交通科技, 2009, 26(10): 59-65.

PENG Hui, SHANG Shou-ping, ZHANG Jian-ren，etal. Test and theoretical research of T-beam strengthened with prestressed CFRP plate[J]. Journal of Highway and Transportation Research and Development, 2009, 26(10):59-65. (In Chinese)

[6] 彭晖,尚守平. 预应力碳纤维板加固受弯构件的试验研究[J]. 工程力学, 2008,25(5): 142-150.

PENG Hui, SHANG Shou-ping. Experimental study of reinforced concrete beam with prestressed CFRP plate[J]. Engineering Mechanics, 2008, 25(5): 142-150. (In Chinese)

[7] BOUCHIKHI A S, LOUSDAD A, MEGUNI A. On the reduce of interfacial shear stresses in fiber reinforced polymer plate retrofitted concrete beams [J]. Materials and Design, 2010, 31(3): 1508-1515.

[8] 杨奇飞. FRP-混凝土黏结界面研究的两个重要问题[D]. 汕头：汕头大学土木工程系，2009: 78-84.

YANG Qi-fei. Two important issues in FRP-concrete interfacial bond[D]. Shantou: Department of Civil Engineering, Shantou University, 2009: 78-84. (In Chinese)

[9] 叶锋, 姚谏. 板宽对FRP-混凝土黏结界面应力影响的三维有限元分析[J]. 科技通报, 2008, 24(6):853-859.

YE Feng, YAO Jian. A 3D finite element study on the effect of FRP plate width on interfacial stress between FRP and concrete[J]. Bulletin of Science and Technology, 2008, 24(6): 853-859. (In Chinese)

[10]YUN Yan-chun, WU Yu-fei, TANG Wai-ching. Performance of FRP bonding systems under fatigue loading [J]. Engineering Structures, 2008, 30:3129-3140.

[11]陆新征, 叶列平, 滕锦光. FRP-混凝土界面黏结滑移本构模型[J]. 建筑结构学报, 2005, 26(4):10-18.

LU Xin-zheng, YE Lie-ping, TENG Jin-guang. Bond-slip model for FRP-to-concrete interface[J]. Journal of Building Structures, 2005, 26(4): 10-18. (In Chinese)

[12]李春霞, 晏石林, 周毓倩. CFRP抗弯加固混凝土梁的界面应力分析[J]. 武汉理工大学学报, 2010, 32(23):35-38.

LI Chun-xia, YAN Shi-lin, ZHOU Yu-qian.Analysis for interfacial stress in concrete beams flexural strengthened by CFRP[J]. Journal of Wuhan University of Technology, 2010, 32(23): 35-38. (In Chinese)

[13]NAKABA K, TOSHIYUKI K, TOMOKI F,etal. Bond behavior between fiber reinforced polymer laminates and concrete [J]. ACI Structural Journal, 2001, 98(3) :359 -367.

[14]UEDA T, DAI J G, SATO Y. A nonlinear bond stress-slip relationship for FRP sheet-concrete interface[C]//Proc Int Symp on Latest Achievement of Technology and Research on Retrofitting Concrete Structures. Kyoto, Japan, 2003:113 -120.

[15]LU X Z, TENG J G, YE L P,etal. Intermediate crack debonding in FRP-strengthened RC beams: FE analysis and strength model[J]. Journal of Composites for Construction, 2007, 11(S):161-174.

[16]GODAT A, LABOSSIÉRE P, NEALE K W,etal. Behavior of RC members strengthened in shear with EB FRP: assessment of models and FE simulation approaches[J].Computers and Structures, 2012, 92/93: 269-282.

[17]NAKABA K, TOSHIYUKI K, TOMOKI F,etal. Bond behavior between fiber-reinforced polymer laminates and concrete[J]. ACI Structural Journal, 2001, 98(3): 359-367.

[18]MONTI M, RENZELLI M, LUCIANI P. FRP adhesion in uncracked and cracked concrete zones[C]//Proceedings of 6th International Symposium on FRP Reinforcement for Concrete Structure. Singapore: World Scientific Publications, 2003:183-192.

[19]SAVIOA M, FARRACUTI B, MAZZOTTI D. Non-linear bond-ship law for FRP-concrete interface[C]//Proceedings of 6th International Symposium on FRP Reinforcement for Concrete Structures. Singapore: World Scientific Publications, 2003:163-172.

[20]DAI J, UEDA T, SATO Y. Development of the nonlinear bond stress-slip model of fiber reinforced plastics sheet-concrete interfaces with a simple method[J]. Journal of Composites Construction, 2005, 9(1): 52-62.

[21]DSI J, UEDA T. Local bond stress relations for FRP sheets-concrete interface[C]//Proceedings of 6th Internation Symposium on FRP Reinforcement for Concrete Structures. Singapore: World Scientific Publications, 2003:143-152.