成层地基中单桩受扭弹塑性分析*

邹新军，徐洞斌，王亚雄

(湖南大学 土木工程学院，湖南 长沙 410082)

为满足我国基础建设发展及不断增加的资源需求，立交桥、海上钻井平台和风力发电塔等结构物不断出现于人们视野.这些结构物多采用桩基础，且由于所处受力环境的特殊性(如互通式立交匝道桥的斜桥或弯桥桩基所受的扭矩；海洋桩基因回旋的风、水流或波浪产生的扭矩)及不均匀侧向力作用等原因，导致其桩基承受较大扭矩作用.工程设计中若忽略这类扭矩荷载影响，可能导致基础及上部结构偏于不安全.事实上，就曾有因忽略风力引起的扭矩作用而导致桩基破坏的报道[1].因此，研究桩基受扭问题，特别是扭矩与竖向力、弯矩及水平力的共同作用具有重要的意义[2].但鉴于问题的复杂性，研究单桩受扭性能仍具有基础性意义.

对于单桩受扭问题的研究，目前已取得一些成果.Poulos[3]和Randolph[4]基于弹性连续介质理论提出了求解单桩扭转刚度的解析方法，但这些研究主要针对单层均质地基，不能应用于实际工程中常见的层状地基.Hache[5]和Chow[6]等虽考虑地基分层特性分别采用桩身微段平衡法和离散元法分析了双层地基的单桩受扭问题，然其解答也仅适用于桩侧土体的弹性阶段.Guo[7-8]等采用桩身微段平衡法和剪切位移法，基于假定的桩侧土剪切模量和极限摩阻力分布形式导得单层与双层地基中桩侧土处于弹性和塑性阶段的解答，对于实际工程中的多层地基，该法仍然无法推广.陈胜立等[9-10]采用积分变换和传递矩阵方法求得成层土在内部环形荷载作用下的基本解后，再基于桩土位移协调条件提出了层状地基中单桩扭转变形的半解析方法，但该法仅假定桩侧土处于弹性阶段，且对于桩-土接触面位移非协调的塑性阶段未给出解答.为此，本文采用桩身荷载传递双折线模型，基于平衡原理等导出桩侧土处于弹性阶段时桩顶扭矩T-扭转角φ关系曲线、以及桩身扭矩与扭转角的分布解答.然后，以桩侧土中塑性区开展深度为变量，探讨成层地基中桩侧土处于塑性状态时桩顶T-φ曲线和桩身扭矩及扭转角计算方法，由此对比分析单层和双层地基中的单桩受扭性能.最后，结合工程算例进行应用，并通过参数分析探讨桩身受扭性能的主要影响参数及其影响规律，以期对桩基受扭问题获得进一步的认识.

1 均质地基中的单桩受扭分析

荷载传递法最先由Seed和Reese[11]根据实验结果提出，且广泛应用于竖向受荷桩[12-15].Georgiadis等[16-17]在总结已有荷载传递法的基础上，将其引入单桩受扭分析，并分别采用了双折线和指数非线性两种模型(如图1).同时，对均质各向同性弹性介质中的桩给出了土体初始抗扭刚度k0的计算式：

(1)

式中Gs为桩侧土的剪切模量；r0为桩径(m).

按桩身荷载传递机理，桩身扭矩和扭转角一般随深度增加而减小，且桩侧土的塑性区也沿深度逐步展开[7].为此，本文采用图1中的双折线模型即理想弹塑性模型，推导成层地基中受扭单桩在桩侧土分别处于弹性及塑性状态时的T-φ曲线、桩身扭矩和扭转角计算公式.

图1 Ts-φ 曲线

1.1 桩-土体系模型及其假定

图2所示为单桩受扭分析模型，其中T为桩顶扭矩(kN·m)；x为深度坐标(m)；L为桩长(m).

桩侧土抗力采用双折线模型模拟，相应的荷载传递函数为：

(2)

式中Ts为桩身扭矩(kN·m)；k为桩侧土抗扭刚度，其取值范围为[ku,k0]，其中ku=Tsu/φu，Tsu可由实测的桩身环向极限侧阻力τsu确定(Tsu=r0τsu)，无实测资料时可近似取k0作为桩侧土抗扭刚度(后文的计算均取k0)；φ和φu分别为桩身的扭转角和弹性极限扭转角(rad)，某一桩段的弹性极限扭转角φui可采用下式简化计算：

(3)

式中φ0为桩顶扭转角；εi为i点的环向应变，无实测资料时可采用近似取法.洪毓康等[18]基于灌注桩原位试验结果建议的极限位移值约为2～15 mm，则可近似取(0.002～0.015)/r0作为极限扭转角.

图2 单桩受扭分析模型

此外，为进一步简化分析，另作如下假定：1)桩-土体系的破坏以桩侧土进入完全塑性阶段为准；2)同一土层的物理力学参数沿深度不变(即均质地基或分层均质地基)，且随桩顶扭矩增加，桩侧土由上而下逐渐进入塑性状态；3)桩侧土处于弹性阶段时桩-土位移协调.

1.2 桩侧土体处于完全弹性状态

桩顶扭矩较小时桩侧土处于弹性受力状态，由桩身单元体的平衡条件等可导得桩身扭转控制方程及边界条件分别如下：

(4)

式中TB,φB分别为桩端处的扭矩和扭转角；Gp,Jp分别为桩身的材料剪切模量和极惯性矩.

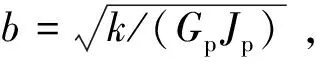
(5)

引入桩端边界条件[4]：

TB=KBφB

(6)

式中系数KB=16GsBr03/3，其中GsB为桩端处桩侧土的剪切模量.

而桩顶扭矩T和扭转角φ可由式(5)导得：

(7)

则桩顶处桩身扭矩与扭转角之比为：

(8)

1.3 桩侧土体部分进入塑性阶段

桩顶扭转角大于φu时，随桩顶扭矩的增加，桩侧土由浅至深逐渐进入塑性阶段(如图3)，假定以D点为界：其上OD段为塑性区，桩-土接触面出现位移非协调；以下DB段为弹性区，现分段分析如下：

图3 桩侧土部分进入塑性状态

1)处于塑性阶段的OD段

当OD段桩侧土处于塑性阶段时，可导得桩身扭转控制方程及边界条件如下：

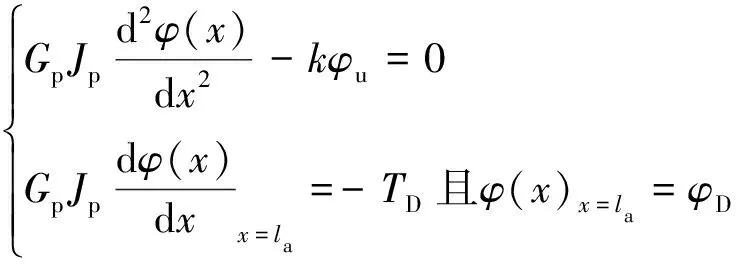
(9)

式中TD,φD分别表示D点处桩身的扭矩和扭转角；la为塑性区开展深度(m).

求解式(9)可得：

(10)

2)处于弹性阶段的DB段

因DB段桩侧土处于弹性阶段，可直接应用式(7)～式(8)所示弹性解答，即以(L-la)代替L代入即可.

综合上述分段解答，则可导出桩顶的扭矩和扭转角分别为：

(11)

式中TD=KDφD，

(12)

2 成层地基中的单桩受扭分析

2.1 成层地基中桩顶T-φ曲线

如图4所示，当la=0时，表示桩顶处桩侧土处于弹塑性状态的临界点.

图4 成层地基桩侧土部分进入塑性阶段

1)桩侧土处于弹性阶段

桩侧土处于弹性阶段，同理可导得第i个桩段桩身扭转控制方程及边界条件为：

(13)

(zi-1≤x≤zi)

(14)

则第i桩段顶部的扭矩Ti和扭转角φi分别为：

(15)

进而可得zi-1深度处桩身扭矩与扭转角之比为：

(16)

2)桩侧土处于塑性阶段

由以上分析，当桩侧土处于塑性状态时可得：

(17)

式中φui表示i桩段的弹性极限扭转角；zi-1,zi分别为i桩段顶、底的深度(m).

2.2 成层地基中桩身扭矩和扭转角

某一桩顶扭矩作用下，可导得弹性阶段第i+1桩段顶截面的扭矩和扭转角递推公式为：

(18)

当桩侧土体处于塑性阶段的桩段，基于式(17)可导得：

(19)

结合式(18)和式(19)，即可得到某一桩顶扭矩作用下的桩身扭矩和扭转角沿深度的分布解答.

2.3 成层地基中桩身受扭分析计算步骤

综合以上解答，为计算成层地基中桩顶T-φ曲线、桩身扭矩和扭转角沿深度的分布曲线，基于Mathcad编制了计算程序，其主要步骤如下：

1)根据地层分布将桩身先初步划分成n个单元，确定每个桩段的几何力学参数(li,Gp,Jp,Gs)及荷载传递模型参数(k0,φui).

2)以塑性区开展深度la为变量，计算桩顶的T-φ曲线和桩身扭矩扭转角分布曲线.la=0时，取桩顶扭转角为弹性极限扭转角φu，按式(18)递推计算弹塑性临界扭矩值.

3)计算la>0时即弹塑性阶段的桩顶T-φ曲线、桩身扭矩和扭转角分布曲线：当la所对应的点位于某个桩段内时，则以该点为界将该桩段再细分成两个桩段，其余桩段划分不变，分别按式(18)和式(19)递推计算弹性区和塑性区的桩身扭矩和扭转角分布曲线.不断增加la进行循环计算，直至la=L时即可获得桩顶的T-φ曲线，由此可作为设计的依据(根据设计规定的桩顶容许扭转角即可确定出相应的桩顶扭矩值，即实现按变形控制设计的思想).

3 方法验证

为验证本文方法，分别将单层和双层地基中的单桩受扭弹性分析结果与已有方法进行了对比.至于塑性分析，将结合工程应用进行验证.

3.1 单层地基中桩身受扭计算对比

对于单层地基中的单桩受扭弹性分析结果，采用不同计算方法时，主要对比其弹性影响因子Iφ[4].

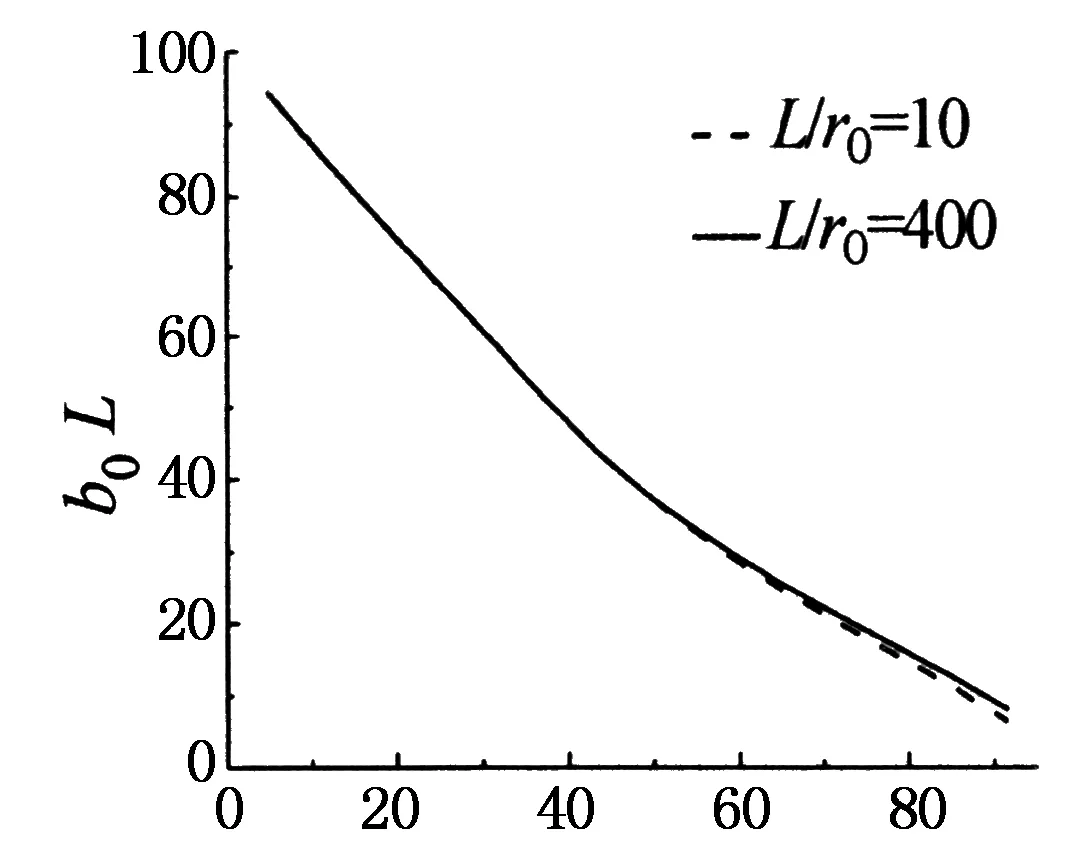
Iφ

3.2 双层地基桩身受扭计算对比

为验证本文成层地基中单桩受扭分析解答，采用文献[6]中的双层地基算例进行验证.参数取值如下：L=25 m，r0=0.5 m，Gp=8 GPa；第二层土剪切模量Gs2=8 MPa.第一层土的厚度h及剪切模量Gs1则通过图6所示的不同比值进行变化.

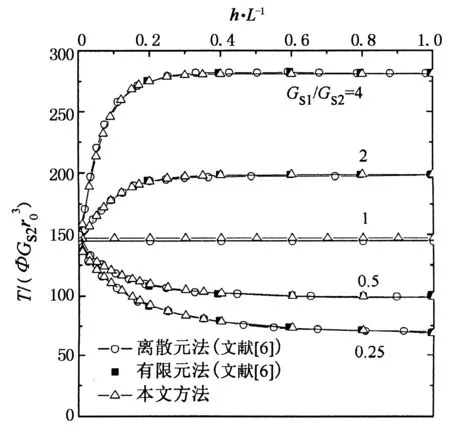
图6 双层地基中桩身受扭对比分析

图6为不同方法所得的桩身扭矩随h/L的无量纲变化曲线，说明本文方法所得结果与文献[6]结果吻合较好.图中结果还表明：双层地基中上、下两层土体的剪切模量比及厚度比均对桩身抗扭性能有较大影响，当Gs1/Gs2值由0.25增至4.0时，桩身抗扭能力可提高约4倍.因此，工程中可对桩侧上部土层进行处理来提高桩身的抗扭性能，从图中的变化规律，该有效处理厚度约为0.2L.

4 参数分析与工程应用

4.1 参数分析

根据所获得的桩身扭矩与扭转角计算公式可知，影响桩身受扭性能的参数主要有桩身材料的剪切模量Gp、桩径r0、桩侧土抗扭刚度k和桩侧土的弹性极限扭转角φu等.下面主要探讨Gp和r0对桩顶T-φ曲线的影响.

1)Gp的影响

参考工程实际应用情况，分别取桩身材料剪切模量为8 GPa,10 GPa,12 GPa,14 GPa和16 GPa进行对比分析.其他参数：L=30 m，r0=0.5 m，k=k0(按式(1)计算)，φu=0.008 rad，Gs=5 MPa.采用所编制的计算程序所得到的不同桩身剪切模量下桩顶的T-φ曲线如图7所示.图中结果表明，桩顶扭矩保持不变时，桩顶扭转角随Gp的增加而减小；而对于某一桩顶扭转位移控制值，桩顶所能承受的扭矩随Gp增大而显著增加，也即桩身抗扭能力不断提高.

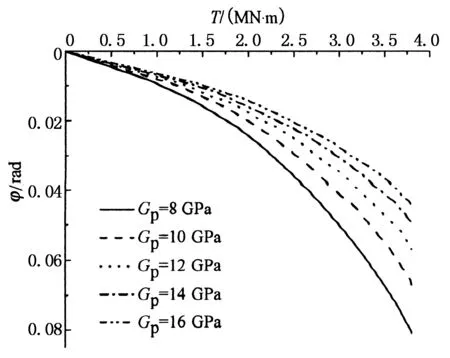
图7 桩身材料剪切模量Gp对桩顶T-φ曲线的影响

2)r0的影响

为探讨桩径的影响，取r0=0.2 m，0.5 m，0.75 m，1.0 m和1.5 m进行对比分析.Gp=14 GPa，其余参数同上.图8给出的桩顶T-φ曲线表明：T一定时，桩顶扭转角随r0增加而显著减小；r0增加一倍时，相同扭转角下桩顶能承受的扭矩值增加4～6倍.

图8 桩径r0对T-φ曲线的影响

4.2 工程算例

为进一步验证本文方法，以文献[19]中锡宜高速宜兴互通大桥1#试桩为例进行计算.计算参数取值：Gp=12.5 GPa，L=47 m，r0=0.5 m.地质资料及模型参数取值如表1所示.

表1 1#试桩地质资料及模型参数

图9给出了本文方法和文献[9]法的对比计算结果，在弹性阶段两者一致性较好.但由于文献[9]法只能进行弹性分析，而本文方法进一步给出了桩侧土处于塑性状态时的解答，更能切合工程实际.

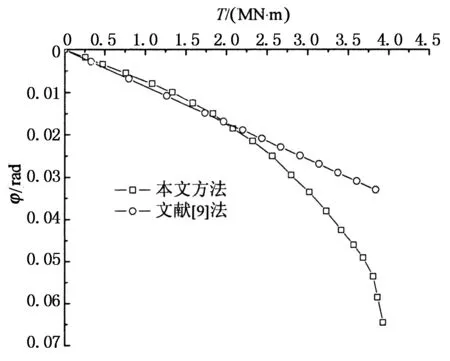
图9 桩顶T-φ曲线对比分析

图10进一步给出了桩顶作用不同扭矩值T0时的桩身扭矩-扭转角分布曲线，其表明：桩顶扭矩沿桩身的传递主要发生在浅部土层中，再次说明处理浅部地基能有效提高桩身抗扭能力.

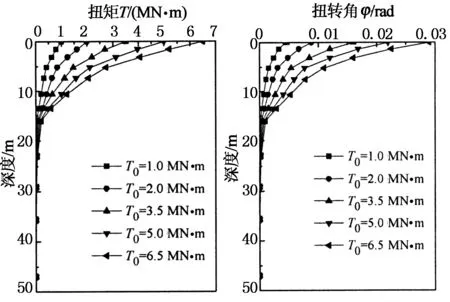
(a)扭矩 (b)扭转角

图10 桩身扭矩和扭转角分布曲线

Fig.10 Distribution curves of the torque and twist angle along the pile shaft under various torque at the pile top

5 结 论

为探讨桩身受扭性能，本文采用双折线荷载传递模型，针对不同桩侧土受力状态，分析了单层与成层地基中受扭单桩的承载性状，主要结论如下：

1)分别建立出单层与成层地基中桩身扭转弹、塑性控制方程，并以桩侧土中塑性区开展深度为基本变量，导得了桩侧土处于弹性与塑性阶段时的桩顶、桩身的扭矩与扭转角计算公式，并基于Mathcad编制出相应的计算程序.

2)通过与已有方法对单层与双层地基中桩身受扭弹性对比分析，验证了本文方法的可行性，且参数分析表明：桩顶扭矩T一定时，桩顶扭转角φ随桩身剪切模量Gp和桩径r0的增加而减小，且r0对T-φ曲线影响显著，相同条件下，r0提高一倍时桩顶可承受的扭矩可提高4～6倍.

3)双层地基中上下两层土体的层厚比及剪切模量比Gs1/Gs2对桩身抗扭性能影响较大，Gs1/Gs2值由0.25增至4.0时桩身抗扭能力提高约4倍.因此，工程中可对桩侧上部土层进行处理来提高桩身的抗扭性能，且有效处理厚度约为0.2倍桩长.

[1]VICKERY B J. Wind effects on building and structures-critical unsolved problems[C]//NAUDOSCHER E，ROCKWELL D.IAHR/IUTAM Practical Experiences with Flow-induced Vibrations Symposium. Karlsruhe: Springer-Verlag, 1979: 823-828.

[2]陈仁朋，郑中，孔令刚，等. 水平及扭转荷载作用下群桩基础受力分析方法[J]. 岩土工程学报, 2013, 35(8):1463-1469.

CHEN Ren-peng, ZHENG Zhong, KONG Ling-gang,etal. Analysis method for pile groups subjected to lateral and torsional loads [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1463-1469.(In Chinese)

[3]POULOS H G. Torsional response of piles [J]. Journal of Geotechnical Engineering Division, ASCE, 1975, 101(10): 1019-1035.

[4]RANDOLPH M F. Piles subjected to torsion [J]. Journal of Geotechnical Engineering Division, ASCE, 1981, 107(8): 1095-1111.

[5]HACHE R A G, VALSANGKAR A J. Torsional resistance of single pile in layered soil [J]. Journal of Geotechnical Engineering, ASCE, 1988, 114(2): 216-220.

[6]CHOW Y K. Torsional response of piles in non-homogeneous soil [J]. Journal of Geotechnical Engineering, ASCE, 1985, 111(7): 942-947.

[7]GUO W D, RANDOLPH M F. Torsional piles in non-homogeneous media [J]. Computers and Geotechnics, 1996, 19(4): 265-287.

[8]GUO W D, CHOW Y K, RANDOLPH M F. Torsional piles in two-layered nonhomogeneous soil [J]. International Journal of Geomechanics, ASCE, 2007, 7(6): 410-412.

[9]陈胜立，张利民. 层状地基中单桩的扭转变形分析[J]. 岩土工程学报, 2005, 27(5): 531-535.

CHEN Sheng-li, ZHANG Li-min. Torsional response of single pile embedded in layered ground [J]. Chinese Journal of Geotechnical Engineering, 2005, 27(5): 531-535. (In Chinese)

[10]陈胜立，寿汉平. 传递矩阵法分析层状地基中桩的扭转变形[J]. 岩土力学,2004, 25(2): 178-186.

CHEN Sheng-li, SHOU Han-ping. Analysis of torsional response of a single pile embedded in layered soil with transfer matrix method [J]. Rock and Soil Mechanics, 2004, 25(2): 178-186. (In Chinese)

[11]SEED H B, REESE L C. The action of soft clay along friction piles [J]. Proceedings of the American Society of Civil Engineers, 1955,122(81): 112-118.

[12]王奎华，吕述晖，吴文兵，等. 层状地基中基于虚土桩模型的单桩沉降计算方法[J]. 工程力学, 2013,30(7):75-83.

WANG Kui-hua, LV Shu-hui, WU Wen-bin,etal. A new calculation method for the settlement of single pile based on virtual soil-pile model in layered soils [J]. Engineering Mechanics, 2013, 30(7): 75-83. (In Chinese)

[13]赵明华，贺炜，邹新军. 计入桩侧摩阻力非线性特性的基桩承载力分析方法[J]. 湖南大学学报：自然科学版, 2007,34(4):5-9.

ZHAO Ming-hua, HE Wei, ZOU Xin-jun. Calculation method for the bearing capacity of pile by considering the nonlinear character of side resistance [J]. Journal of Hunan University ：Natural Sciences, 2007, 34(4): 5-9. (In Chinese)

[14]赵明华，何俊翘，曹文贵，等. 基桩竖向荷载传递模型及承载力研究[J]. 湖南大学学报：自然科学版,2005, 32 (1):37-42.

ZHAO Ming-hua, HE Jun-qiao, CAO Wen-gui,atal. Study on the load transfer model and the bearing capacity of vertically loaded piles[J]. Journal of Hunan University ：Natural Sciences, 2005,32(1):37-42. (In Chinese)

[15]王奎华，罗永健，吴文兵，等. 层状地基中考虑桩端应力扩散的单桩沉降计算[J]. 浙江大学学报：工学版, 2013, 47(3): 472-479.

WANG Kui-hua, LUO Yong-jian, WU Wen-bin,etal. Calculation method for settlement of single pile considering stress dispersion of pile and soil[J]. Journal of Zhejiang University ：Engineering Science， 2013, 47(3): 472-479. (In Chinese)

[16]GEORGIADIS M. Interaction between torsional and axial pile response[J]. Numerical and Analytical Methods in Geomechanics, 1987, 11(6): 645-650.

[17]GEORGIADIS M, SAFLEKOU S. Piles under axial and torsion loads [J]. Computers and Geotechnics, 1990, 9(4): 291-305.

[18]洪毓康，陈强华. 钻孔灌注桩的荷载传递性能[J]. 岩土工程学报, 1985, 7(5): 22-24.

HONG Yu-kang, CHEN Qiang-hua. Load transfer performance of bored pile [J]. Chinese Journal of Geotechnical Engineering, 1985, 7(5): 22-24. (In Chinese)

[19]赵明华，张洋，张永杰. 考虑荷载传递非线性特性的基桩竖向承载力计算[J]. 公路交通科技,2011,28(9):71-76.

ZHAO Ming-hua, ZHANG Yang, ZHANG Yong-jie. Calculation of vertical bearing capacity of piles with consideration of nonlinear characteristic of load transfer [J]. Journal of Highway and Transportation Research and Development, 2011, 28(9):71-76. (In Chinese)