基于环境振动信号的框架结构震后损伤识别*

陈清军，周成杰，杨永胜

(同济大学 土木工程防灾国家重点实验室，上海 200092)

我国是一个地震灾害频发的国家，城市中建筑结构密集.在高烈度地震发生后，能够对震后灾区的建筑结构进行快速有效的损伤诊断显得非常重要.传统的结构损伤识别方法，往往采用结构的自振频率、阻尼比、振型、质量和刚度矩阵等作为损伤指标，虽然这些损伤指标理论上可以用来识别损伤，但实际工程中由于测试误差和噪音等因素很难准确地获得这些物理参数[1].

近年来，随着小波包分解理论的应用，基于结构振动信号的损伤识别方法逐渐得到了重视.滕军等[2]对高层结构的加速度信号进行小波包分解，由频带能量变化率指标判别出结构的损伤程度.丁幼亮等[3]对混凝土板损伤前后的动力响应进行小波包分解，由特征频带的能量变化识别损伤.谭冬梅等[4]对输电塔架的结构振动信号进行小波包分解和聚类分析识别出了输电塔架的多个损伤工况.Hae等[5]利用小波变换分解结构振动信号，根据时域内的能量分布构建损伤指标，对4层钢框架结构进行了损伤识别分析.这些研究是通过对振动信号进行小波包分解或者小波变换得到频域或时域内能量分布，由结构损伤前后能量分布的改变情况构建损伤指标.但在实际工程应用中存在以下两个问题：第一，难以对大型结构施加动荷载；第二，难以保证结构损伤前后的激励完全一致.

众所周知，地球表面无时无刻都在作不规则的微弱振动，这种振动的产生可以认为是气象变化、潮汐、海浪等自然力和交通运输、动力机器、爆破冲击等人为振源经地层介质多重反射和透射、由四面八方传播到测试点的各种谐波集合而成，随时间作不规则的微弱振动，可理解为横波在场地表土层中的多重反射结果，具有平稳随机过程的性质[6].由此，本文探索以环境振动作为激励信号，采用小波包分解和概率统计相关理论，利用框架结构损伤后振动信号的能量在频域内的变化构建损伤指标DI，进行钢筋混凝土框架结构的震后损伤识别分析，以避免上述的两个缺陷.

1 振动信号的小波包分解

对振动信号S进行n层小波包分解，第n层有j=2n个一定宽度的频率带(频带)，提取各频带的小波包分解系数重构可以得到各频带的子信号Snj.假定对一时域信号S进行3层小波包分解，并对小波包分解系数进行重构，则总信号可以表示为：

S=S31+S32+…+S38

(1)

其中S为总信号；S31,S32,…,S38为子信号.

第j个频带的能量Ej可由子信号Snj得到[3]：

(2)

其中xjk为第j个频带子信号的第k个离散点的值；N为第j个频带子信号的总点数.

由理论分析可知[3]，采用各频带的能量与总能量之比构造的小波包能量谱具有损伤敏感性和噪声鲁棒性.第j频带的小波包能量比(Wavelet Packet Energy Ratio, WPER)定义为:

(3)

其中Ej表示第j个频带的能量;n表示小波包分解的层数.

2 损伤指标的定义与损伤识别方法

将结构损伤前后能量比的变化(Energy Ratio Variation, ERV)作为损伤识别的参量，即

(4)

在式(4)的基础之上，定义能量比偏差ERVD[3]：

(5)

当结构损伤前后的激励相同时，能量比偏差ERVD可以有效地识别结构损伤[3].但在实际工程中，结构损伤前后的激励往往难以做到完全相同.因此，本文对同种工况多组激励下的ERVD求置信上限，并以此置信上限作为损伤指标的参量.

(6)

在式(6)的基础上，定义最终的损伤指标 (Damage Indicator, DI)：

(7)

综合上述的振动信号小波包分解理论和损伤指标定义，可以以如图1所示的流程图形式给出本文的损伤识别方法.由图1可知，本文方法实际上是利用结构损伤后振动信号的能量在频域内的变化，并由此构造损伤指标DI.

图1 损伤指标DI构造流程图

3 框架结构模型及其易损部位

本文以汶川县某中学教学主楼为例进行震后损伤识别分析.这是一个8层的混凝土框架结构，地上总高度为30 m，底层层高4.8 m，其余层高3.6 m.利用ANSYS有限元软件建模，梁柱采用beam188单元，板采用shell63单元，有限元模型如图2所示.

图2 结构有限元模型

这里首先通过框架结构地震反应数值分析确定易损部位.输入图3所示的4条地震波，对框架结构进行时程响应分析.图4给出了该结构层间位移角沿楼层的包络图.由此可见，在4条不同地震波作用下该结构底层的层间位移角均为最大，表明结构底层为易损部位.这与“5.12”汶川大地震中钢筋混凝土框架结构的震害现象[7]和相关试验研究结果[8]相符.

T/s

层间位移角/rad

综合数值模拟和震害现象分析，本文通过改变底层柱的抗剪承载力来模拟大震作用后结构发生的损伤，并设定表1所示的5种工况，其中工况1为完好结构，工况2～工况5表示损伤程度的递增.

表1 损伤工况

4 结构损伤识别及其影响因素分析

4.1 无损结构的小波包能量比均值

根据本文的损伤识别方法(见图1的损伤识别流程图)，首先计算无损结构的小波包能量比均值.

对无损结构沿纵向(x轴)输入20条不同的环境激励时程，其采样频率为100 Hz，持续时间为15 s，峰值为1(10-2m/s2)，其中一条激励时程如图5所示.利用图2所示的有限元模型，求得20条结构顶层的纵向(x轴)加速度响应时程和20条速度响应时程，其中一组的加速度响应时程和速度响应时程如图6所示.

时间/s

时间/s

时间/s

当采用结构速度响应时程时，相应的小波包能量比及其均值如图8所示，由此可见，当采用结构速度响应时程时，其能量基本上集中在低频区域.

4.2 结构的损伤识别

根据表1所示的各损伤工况，对无损和有损结构分别输入10条不同的环境激励时程.由ANSYS软件计算得到顶层楼板x方向的加速度时程和速度时程样本信号.按照图1所示的流程，可以得到各工况的能量比偏差ERVD及其置信上限.

(a)小波包能量比

频带

(a)小波包能量比

频带

图9表示工况1～工况5分别在10个不同激励样本下，得到的能量比偏差ERVD及其置信上限.考虑到建筑工程结构的误差，本算例的置信度取95%，利用t分布表可得式(6)中的λ值为1.812.

图9(a)采用了顶层加速度时程，图9(b)采用了顶层速度时程.由图9可知，无损工况(工况1)的能量比偏差总体上是大于其他有损工况的.由于输入的激励是10条不同的环境激励，所以同一工况的能量比偏差也是在一定范围内波动的.因此用各工况的置信上限代表各工况的能量比偏差.将图9所示的置信上限代入式(7)，可得最终的损伤指标DI,如图10所示.

激励样本序号

激励样本序号

图10(a)和图10(b)分别是采用加速度时程和速度时程的损伤识别结果.图10(a)的损伤指标DI介于0.75到1之间；图10(b)的结果介于2.5到4.5之间，并且，损伤指标DI随着损伤程度的变大而变大.因此，损伤指标DI可以识别结构的损伤.

4.3 取不同楼层振动信号对损伤识别效果的影响

图10为取顶层的振动信号时得到的损伤指标．同样的，也可以得到其他1～7楼层的结果，如图11所示.从图11的两张图均可看出，各楼层对应的曲线形状相似，数值大小有显著差异，且楼层越高则DI越大.例如，图11(a)第1层的数值在0到0.1之间，而第8层是0.7到0.9之间，两者数值相差较大；图11(b)的第1层的数值在1.5到3.5之间，而第8层在2.5到4.5之间，两者数值相差较大.

柱失去的抗剪强度百分比/%

柱失去的抗剪强度百分比/%

由于损伤指标DI的数值愈大所对应的损伤识别效果愈好，因此，建议取结构顶层的振动信号作为损伤识别用的分析信号.

4.4 不同类型信号对损伤识别效果的影响

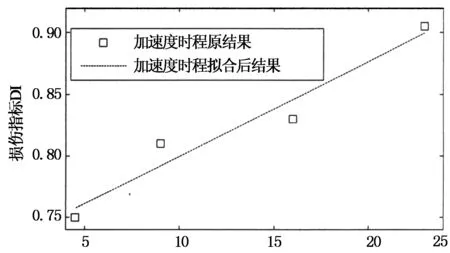
这里选取结构顶层的速度响应时程和加速度响应时程，利用损伤指标与损伤程度的拟合结果，探讨不同类型信号对损伤识别效果的影响.

提取结构顶层的损伤指标与损伤程度曲线，通过MATLAB程序可用多项式拟合出如下两式：

DIa=0.77d+0.72

(8)

DIv=9.19d+2.12

(9)

其中d为损伤程度;DIa为加速度时程对应的损伤指标;DIv为速度时程对应的损伤指标.

由式(8)拟合出的直线斜率为0.77，由式(9)拟合出的直线斜率为9.19，表明速度信号比加速度信号对损伤变化更为敏感.

图12给出了损伤指标与损伤程度的拟合结果，其中图12(a)为对应式(8)的结果，图12(b)为对应式(9)的结果.两者拟合的残差分别为5.73%和2.15%，后者更接近线性，即速度时程的结果更接近线性，因此，速度信号对损伤程度的识别效果比加速度的更好.

柱失去的抗剪强度百分比/%

柱失去的抗剪强度百分比/%

柱失去的抗剪强度百分比/%

柱失去的抗剪强度百分比/%

5 结 论

针对钢筋混凝土框架结构的震后损伤识别问题，本文建立了一种基于环境振动信号的小波包分解损伤识别方法，并以某钢筋混凝土框架结构为例，对框架结构进行了震后损伤识别分析，探讨了不同楼层、不同类型振动信号对损伤识别效果的影响.通过本文的算例分析，可以得到如下初步结论：

1)利用文中构建的损伤指标DI可以有效识别框架结构的损伤，损伤指标DI与损伤程度之间有近似线性的关系.

2)选取不同楼层的振动信号对损伤识别效果有较大影响.基于较高楼层振动信号的损伤指标值对结构的损伤识别效果较好，建议采用结构顶层的振动信号构造损伤指标.

3)在本文算例中，速度信号比加速度信号对损伤变化更为敏感；基于速度信号的损伤指标与损伤程度的拟合结果，较基于加速度信号的拟合结果更接近线性，识别效果更好.

[1]宗周红，任伟新，阮毅．土木工程结构损伤诊断研究进展[J].土木工程学报，2003，36(5)：105-110．

ZONG Zhou-hong, REN Wei-xin, RUAN Yi. Recent advances in research on damage diagnosis for civil engineering structures[J]. China Civil Engineering Journal, 2003, 36(5):105-110.(In Chinese)

[2]滕军，何春凯．高层结构震后损伤的小波包分析模糊评价方法[J]．土木建筑与环境工程，2010，32(12)：469-471．

TENG Jun, HE Chun-kai. Wavelet packet analysis of earthquake damage of high-rise structures based on fuzzy evaluation method[J]. Journal of Civil Architectural & Environmental Engineering, 2010, 32(12):469-471.(In Chinese)

[3]丁幼亮，李爱群，缪长青．基于小波包能量谱的结构损伤预警方法研究[J]．工程力学，2006，23(8)：42-48．

DING You-liang, LI Ai-qun, MIAO Chang-qing. Investigation on the structural damage alarming method based on wavelet packet energy spectrum[J]. Engineering Mechanics, 2006, 23(8): 42-48.(In Chinese)

[4]谭冬梅，瞿伟廉，秦文科．基于小波包和模糊聚类的输电塔架结构损伤诊断[J]．天津大学学报，2011，44(8)：695-700．

TAN Dong-mei, QU Wei-lian, QIN Wen-ke. Damage identification of transmission tower based on wavelet packet transform and fuzzy clustering [J]. Journal of Tianjin University, 2011, 44(8): 695-700.(In Chinese)

[5]YONG N H，KRISHNAN N K， LIGNOS D G，etal. Use of wavelet-based damage-sensitive features for structural damage diagnosis using strong motion data[J]. Journal of Structural Engineering, 2011,137(10):1215-1228.

[6]中国工程建设标准化协会建筑振动专业委员会．建筑振动工程手册[M]．北京：中国建筑工业出版社，2002:586-588.

Branch of architectural vibration, China association for engineering construction standardization. Building vibration engineering handbook[M]. Beijing: Chinese Building Industry Press, 2002:586-588.(In Chinese)

[7]熊立红，杜修力，陆鸣，等．5．12汶川地震中多层房屋典型震害规律研究[J]．北京工业大学学报，2008，34(11)：1166-1172．

XIONG Li-hong, DU Xiu-li, LU Ming,etal. Damage of multistory buildings during the 2008 Wenchuan earthquake[J]. Journal of Beijing University of Technology, 2008, 34(11):1166-1172.(In Chinese)

[8]齐岳，郑文忠．低周反复荷载下核心高强混凝土柱抗震性能试验研究[J] ．湖南大学学报:自然科学版，2009,36(12):6-12.

QI Yue, ZHENG Wen-zhong. Experimental study of the seismic behavior of concrete columns with high strength core under low cyclic loading[J]. Journal of Hunan University:Natural Sciences, 2009,36(12):6-12.(In Chinese)