阵风条件下高超声速飞行器动力学建模与分析

程璞, 张鹏宇, 吴小华, 黄兴李, 闵昌万

(空间物理重点实验室, 北京 100076)

0 引言

高超声速飞行器的气动特性复杂、飞行环境不确定性大、横侧向耦合性强,对迎角和侧滑角等有严格的限制[1-2]。在阵风作用下,飞行器的迎角和侧滑角将产生相应的波动,需要飞行控制系统具有较强的鲁棒性,以保证在阵风干扰下飞行器仍能够稳定飞行。由于飞行试验的高成本、高风险性,合理地设计阵风模型,充分考核飞行控制系统的鲁棒性,是研制单位的重要工作之一,这需要深入研究阵风干扰对高超声速飞行器闭环稳定性的影响机理。

基于所研究飞行器的模型、飞行任务及飞行环境的特点,文献[3-6]主要考虑了阵风对飞机载荷的影响以及减缓控制方法,文献[7]建立了轴对称导弹气动伺服弹性系统的连续与离散阵风响应分析方法,文献[8]推导了考虑风场情况下的飞行器六自由度动力学方程,并通过仿真研究了系统的特性。

本文针对面对称高超声速飞行器的特性,建立了阵风条件下的飞行器动力学模型,研究了阵风对系统闭环稳定性的影响机理,可为高超声速飞行器控制系统仿真考核、控制器设计等提供依据。

1 阵风干扰的等价作用

阵风干扰改变了飞行器相对气流速度的大小和方向,从而改变了飞行器受到的气动力,并对飞行器的控制产生影响。设飞行器相对地球的速度大小为V,在弹体系下的分量为(Vx1,Vy1,Vz1),风速在弹体系下的分量为(u,v,w),则有:

(1)

设风速远小于飞行器速度,将式(1)进行泰勒展开,并忽略高阶项后得到:

(2)

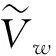
表1 阵风干扰的等价作用Table 1 Equivalent effect of gust

2 考虑阵风后的飞行器控制模型

2.1 基本假设

为了更好地反映阵风对系统稳定性的影响,并使得相关分析具备一般性,基于高超声速飞行器的特点,作如下假设:飞行器为面对称飞行器,横侧向耦合严重,纵向与横侧向通道耦合较小;飞行器为理想刚体,忽略结构弹性变形影响,忽略飞行器结构偏差;飞行器利用俯仰舵偏控制纵向通道,利用差动舵偏控制横侧向通道;忽略地球自转,且地球为均匀重力场,重力加速度为常量。

2.2 阵风条件下闭环系统的控制模型

为分析阵风对系统主要状态量的影响机理,对非线性模型进行线性化,得到纵向短周期模态及横侧向系统的状态方程为:

(3)

(4)

式中:α,β和γv分别为迎角、侧滑角和倾侧角;δφ和δγ分别为俯仰舵偏角和差动舵偏角;ωx1,ωy1和ωz1分别为滚转角速度、偏航角速度和俯仰角速度;Yα,Mα,Zβ等为动力学导数。

设αE和βE分别为不考虑风干扰情况下的迎角和侧滑角,则有:

Δα=ΔαE+Δαw， Δβ=ΔβE+Δβw

(5)

根据表1和式(5),纵向短周期模态和横侧向系统的线性化模型分别转化为:

(6)

(7)

设控制律为Δδφ=kαΔαE+kωzΔωz1,Δδγ=kγvΔγv+kωxΔωx1+kβΔβE+kωyΔωy1,根据式(6)和式(7),得到闭环情况下系统的动力学模型为:

(8)

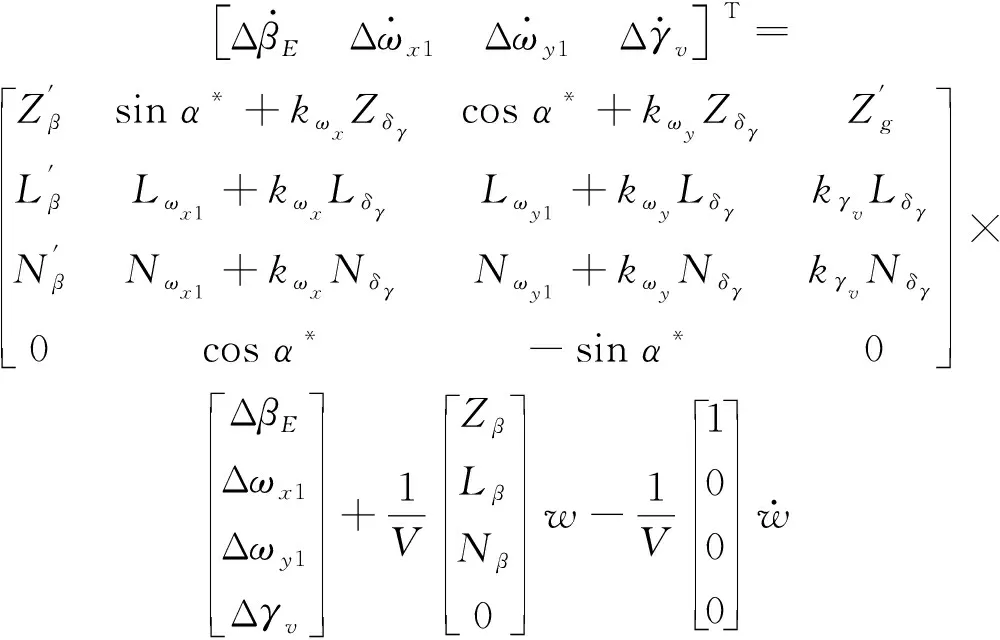
(9)

其中:

根据式(8)、式(9)可以得到αE(s)/u(s),αE(s)/v(s)和βE(s)/w(s),则有:

(10)

基于式(10),可以分析闭环情况下阵风(u,v,w)对α和β的影响。

3 阵风对闭环系统的影响分析

阵风对高超声速飞行器闭环控制系统的影响程度取决于其引起的迎角和侧滑角的变化。迎角和侧滑角的变化幅值越大,阵风对系统稳定控制的不利影响就越大。极端情况下,当阵风导致的气流角变化超出飞行器的控制能力时,飞行器就会失稳。

系统对阵风的抑制作用会随着频率的不同而不同。在一定频率范围内,系统能够有效抑制阵风的干扰。系统对不同频率阵风干扰的响应情况是由阵风到系统状态量的传递特性(包括α(s)/u(s),α(s)/v(s)和β(s)/w(s))所决定的。同时,作为一种瞬态干扰,阵风模型的形式和参数直接影响其能量在不同频率范围内的分布。因此,阵风到系统状态量的传递特性和阵风的频谱分布共同决定着风干扰对飞行器状态量的改变程度,可以通过频域分析研究阵风对闭环系统的影响。

3.1 阵风模型参数对频谱分布的影响

阵风剖面的几何形状有矩形、三角形、梯形等[9-11]。本文考虑矩形、三角形和梯形形状的阵风模型,如图1所示。图中,d3≥d2≥d1≥d0,d3-d2=d1-d0。当d3-d2=d1-d0=0时,阵风剖面形状为矩形;当d2=d1时,剖面形状为三角形。其余情况下剖面的形状为梯形,即矩形波和三角波是梯形波的特例。

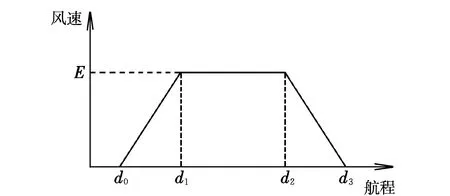
图1 阵风剖面几何形状Fig.1 Gust profile

根据当前飞行器的飞行速度V0,可以将阵风Vg(d)变为时间的函数Vg(d)=Vg(V0t),并进行傅立叶频谱分析。设梯形波为:

(11)

在τ+τ1一定的条件下,图2给出了梯形波频谱分布随τ1:τ的变化情况。

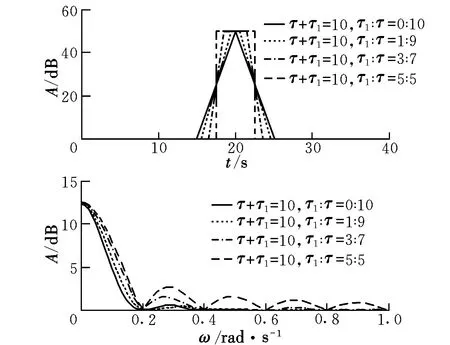
图2 τ1:τ对梯形波频谱分布的影响Fig.2 Effect of τ1:τ on frequency spectrum of trapezoidal wave

可以看到,对矩形、三角形和梯形形状的阵风模型,E,τ+τ1和τ1:τ共同决定了阵风的频谱分布:E直接影响阵风的总能量,E越大,阵风的能量越大;τ+τ1直接决定阵风频谱主旁瓣的截止频率点fc;在τ+τ1一定的情况下,τ1:τ越大,阵风的能量越大(τ1:τ=0时为三角形阵风,τ1:τ=1时为矩形阵风)。

3.2 阵风模型参数对闭环系统的影响

系统响应情况由阵风频谱分布以及阵风到系统状态量的传递特性决定。在控制器设计完成的情况下,阵风到系统状态量的传递特性是确定的,其频谱分布直接决定着系统状态量的变化。阵风干扰在系统敏感频率范围内的能量分布越大,其引起的迎角、侧滑角的变化幅值越大,对闭环系统稳定性的不利影响也越大。因此,针对矩形、三角形和梯形的阵风模型,可以得到如下结论:E越大,阵风能量越大,对系统的影响也越大;当选择τ+τ1使得系统敏感的频率范围落在阵风频谱主旁瓣内时,阵风对系统的影响会较大;τ1:τ越大,阵风对系统的影响越大。

3.3 阵风模型设计原则

在对风场认知不够充分的条件下,应当结合实际环境情况确定对飞行器稳定控制影响尽可能大的阵风模型。此时,为实现对控制系统的有效考核,阵风模型可以按照如下方法进行设计:

(1)针对施加阵风的状态,根据式(8)和式(9)得到对应状态下的α(s)/u(s),α(s)/v(s)和

β(s)/w(s)。

(2)根据传递特性,确定系统对阵风敏感的频率范围f1～f2,即(1)中传递函数幅值较大的频率范围。

(3)在考虑实际环境的情况下,调整阵风模型参数使得阵风在f1～f2频率范围的能量分布尽量大。以梯形阵风为例,可以选择τ+τ1使得0.7≤f2(τ+τ1)/2≤0.9。

(4)根据实际情况选择尽量大的阵风幅值。

4 仿真分析

以某高超声速飞行器典型状态下的模型为例,通过仿真分析模型参数E,τ+τ1,τ1:τ对阵风干扰作用的影响,从而对结论进行验证。

4.1 系统的传递特性分析

针对所研究的飞行器状态,根据式(8)和式(10)可以得到α(s)/v(s),其传递特性如图3所示。可以看到,在0.437 Hz附近,系统对v较为敏感;随着频率增大,系统对v的抑制作用会变大。

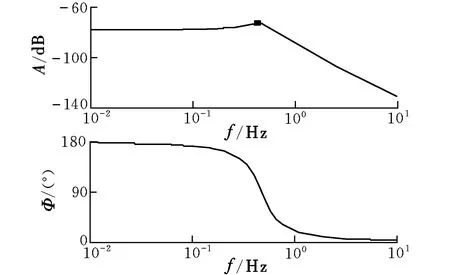
图3 α(s)/v(s)传递特性Fig.3 Transfer function of α(s)/v(s)

4.2 模型参数E对阵风作用的影响

以式(8)作为仿真中使用的动力学模型,分析v对迎角的影响。阵风v的剖面形状为梯形,仿真中取τ+τ1=3,τ1:τ=4:6。

图4给出了不同E下系统的响应情况。可以看到,随着E的增大,阵风的能量逐渐增大,迎角的变化范围也变大。

图4 不同E下系统的响应情况Fig.4 System responses at different E

4.3 模型参数τ+τ1对阵风作用的影响

以式(8)作为仿真中使用的动力学模型,分析v对飞行迎角的影响。阵风v的剖面形状为梯形,仿真中取E=50,τ1:τ=4:6。图5给出了不同τ+τ1下系统的响应情况。可以看到,当τ+τ1=3时,迎角的变化范围最大。

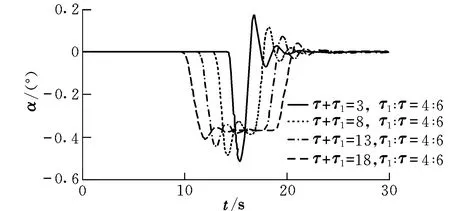
图5 不同τ+τ1下系统的响应情况Fig.5 System responses at different τ+τ1

根据图3,0.437 Hz附近是系统对阵风的敏感区,表2给出了不同τ+τ1情况下阵风频谱主旁瓣的截止频率。可以看到,仿真中只有当τ+τ1=3时,系统对阵风的敏感区都落在了阵风频谱的主旁瓣内,此时迎角的变化也最大。

表2 不同τ+τ1下阵风频谱主旁瓣截止频率Table 2 Cut-off frequency of gust with different τ+τ1

4.4 模型参数τ1:τ对阵风作用的影响

以式(8)作为仿真中使用的动力学模型,分析v对飞行器迎角的影响。阵风v的剖面形状可能为梯形、三角形或矩形,仿真中取E=50,τ+τ1=3。图6给出了不同τ1:τ下系统的响应情况。可以看到,随着τ1:τ的增大,阵风的能量逐渐增大,迎角的变化范围也变大。

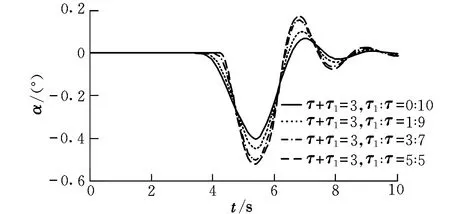
图6 不同τ1:τ下系统的响应情况Fig.6 System responses at different τ1:τ

5 结束语

本文基于高超声速飞行器的特点,建立了考虑阵风干扰后的动力学模型,深入研究了阵风干扰对闭环系统的影响机理,明确了阵风到系统状态量的传递特性,以及阵风的频谱分布共同决定着系统对风干扰的响应情况。在此基础上给出了考核控制系统鲁棒性的阵风模型设计原则,可以为阵风模型的设计等提供依据。

参考文献：

[1] 黄琳,段志生,杨剑影.近空间高超声速飞行器对控制科学的挑战[J].控制理论与应用,2011,28(10):1496-1505.

[2] 吴宏鑫,孟斌.高超声速飞行器控制研究综述[J].力学进展,2009,39(6):756-765.

[3] 费玉华.阵风减缓直接升力控制方案的仿真研究[J].飞行力学,2000,18(1):69-72.

[4] 张军红,李振水,詹孟权,等.LQG控制理论在阵风载荷减缓系统中的应用[J].飞行力学,2007,25(2):61-64.

[5] 宗捷,邹丛青,孙庆民.气动弹性系统的阵风减缓与颤振主动抑制[J].飞行力学,1995,13(4):76-82.

[6] 曹九发.飞机阵风响应仿真计算及载荷减缓技术研究[D].南京:南京航空航天大学,2010.

[7] 吴志刚,杨超.弹性导弹的连续与离散阵风响应[J].北京航空航天大学学报,2007,33(2):136-140.

[8] 程路,姜长生,都延丽,等.变化风场下近空间飞行器机体/发动机一体化飞行力学建模与分析[J].宇航学报,2012,33(5):547-555.

[9] 范培蕾,张晓今,杨涛.高超声速飞行试验风场建模与仿真分析[J].战术导弹技术,2009(2):76-82.

[10] Etkin B.Turbulent wind and its effect on flight [J].Journal of Aircraft,1981,18(5):327-345.

[11] Adelfang S I,Smith O E.Gust models for launch vehicle ascent[C]//AIAA,Aerospace Sciences Meeting and Exhibit,36th.Reno,NV,1998:9-10.