高超声速飞行器非线性动态特性分析
徐敏, 白斌, 祝小平
(1.西北工业大学 航天学院, 陕西 西安 710072;2.西北工业大学 无人机研究所, 陕西 西安 710072)
0 引言
目前大部分高超声速飞行器都具有典型的乘波体机身和矩形进气道超燃冲压发动机一体化设计外形[1]。由于吸气式高超声速飞行器建模涉及到弹性、气动和推进的耦合作用,属于多学科交叉问题,建模难度较大,传统的飞行动力学模型将不再适用。文献[2-4]分别建立了简化的二维高超声速飞行器模型,并进行了相应研究。
在30多年的探索中,作为非线性动力学特性分析的重要工具,分支分析的理论发展经历了两个重要的阶段。1977 年,Mehra等[5]首次提出分支分析与突变理论方法(简称常规分支分析方法),并对飞机大迎角快速滚转的操纵性和稳定性进行了非线性动力学分析。2001年,Ananthkrishnan和 Sinha提出扩展分支分析方法[6],利用此方法可以有效地分析约束飞行状态下的非线性动力学特性,从而弥补常规分支分析方法只能连续变化单一控制参数达不到约束飞行条件这一缺陷。
本文对Bolender和Doman提出的二维高超声速飞行器模型[3]进行纵向分析。首先利用空气动力学相关理论得到气动力和推力数据,进而完成弹性模型计算,最后得到了巡航状态下飞行器的分支图,并针对平衡曲线对系统稳定性和机身弹性的影响进行了简要分析。
1 几何外形描述
如文献[3],纵向剖面视图及机体坐标系Oxyz如图1所示。
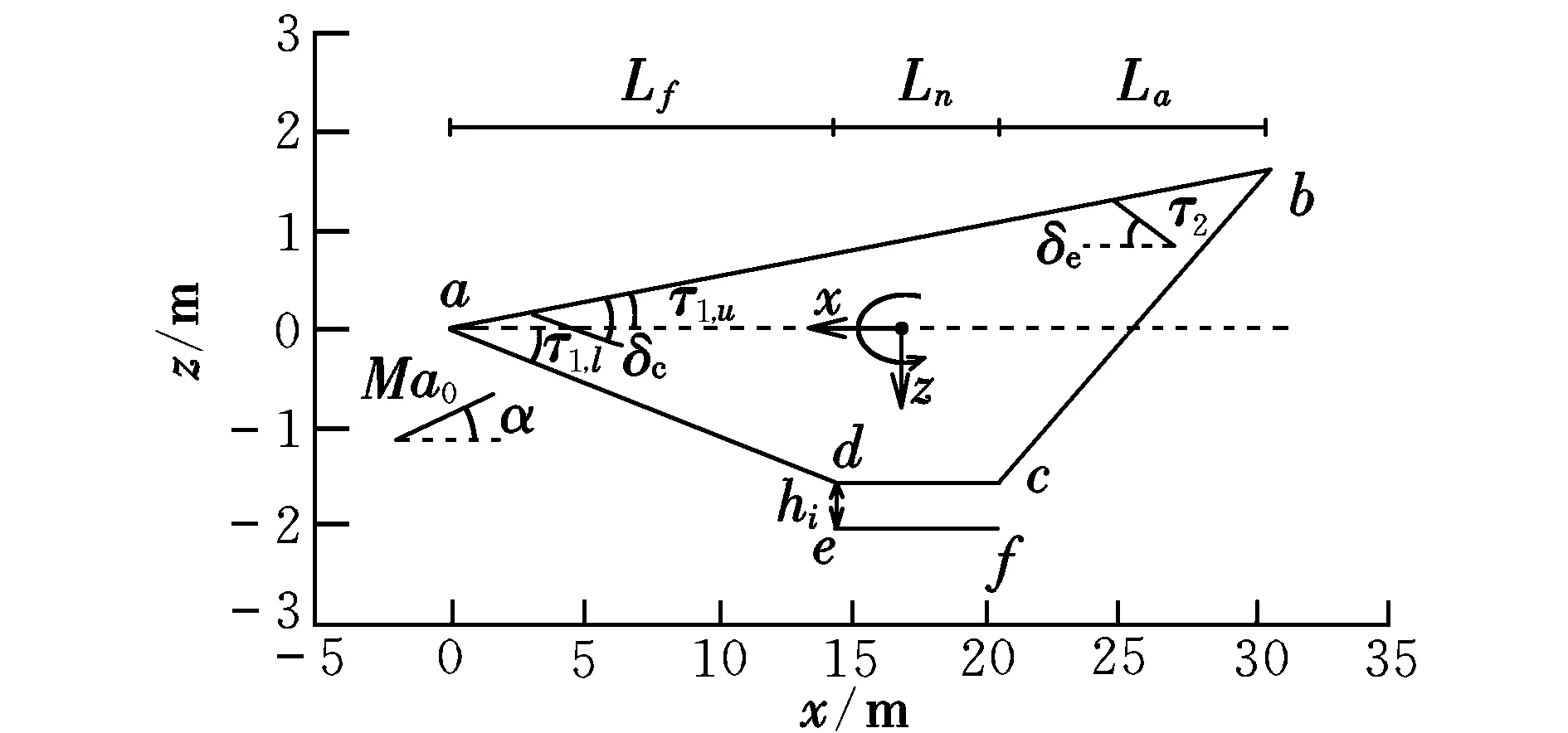
图1 吸气式高超声速飞行器几何外形Fig.1 Geometry of hypersonic air-breathing vehicle
飞行器在 30 km的高度以Ma0=10的速度进行巡航运动。声速计算方法如下:
(1)
式中:γ为比热比,这里为固定值1.4;Ra为空气气体常数287.0041 J/(kg·K)。利用式(1)可以方便地计算出飞行速度V0。
2 气动计算
自由来流流过机体前部下表面ad时,与下表面的夹角为δ=τ1,l+α。当δ>0时,采用Oblique-Shock理论来计算激波后的马赫数Ma1、温度T1和压力P1;当δ<0时,则采用Prandtl-Meyer理论来计算膨胀波后的气体参数。
当δ>0时,气流分布如图2所示。为了实现空气流量的最大化,发动机的进气道唇口需设计为可变结构,使得在不同迎角和马赫数下,机体前端的激波经过唇口前端后产生的激波刚好打在进气口上端前部,以保证进入发动机的气流为一维流。

图2 机体下表面气流分布图Fig.2 Air flow distribution at the lower surface of the vehicle
同理,利用Oblique-Shock理论或Prandtl-Meyer理论可以分别计算出机体上表面ab的压力Pf、发动机下表面ef的压力Pn、机体尾部下表面bc的压力Pa、升降舵δe的压力Pδe和前端鸭舵δc的压力Pδc,进而计算相应的气动力,详见文献[3]。各个初始参数取值范围如表1所示。

表1 各参数取值范围Table 1 Range of the parameters
表1中的ψ为燃油当量比。当Ma0=10,ψ=0.4,δc=0°时,得到升力、阻力和俯仰力矩随迎角、升降舵偏角变化的三维图如图3所示。

图3 升力、阻力和俯仰力矩随迎角、升降舵偏角变化曲线Fig.3 Changes of lift, drag and pitch moment with AOA and elevator deflection
对比文献[7]相应的结果,可以发现两者在走势上是一致的。出现差异的主要原因是本文在机体前部加入了鸭舵δc,同时飞行器的几何参数也有一定的不同。
3 推力计算
发动机模型如图4所示,分为以下3个阶段:A1~A2为气体压缩减速阶段;A2~A3为燃烧室;A3~Ae为气体膨胀加速阶段。
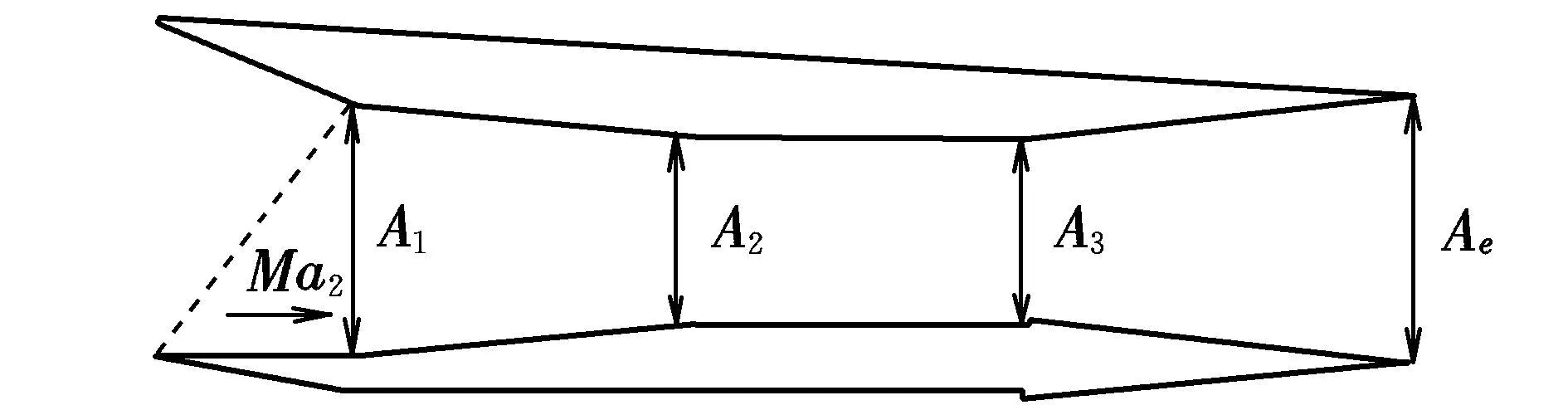
图4 发动机模型Fig.4 Engine model
在A1~A2段,利用连续方程(质量守恒)可以计算出燃烧室入口A2截面处的气体参数Ma3,T3,P3。
A2~A3燃烧室内,为避免碳氢燃料燃烧室产生复杂的物理化学变化给推力的计算带来困难,采用氢气为燃料,根据一维Rayleigh流理论可知:
(2)
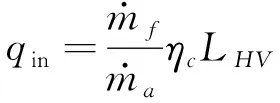
(3)
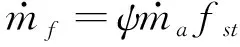
(4)
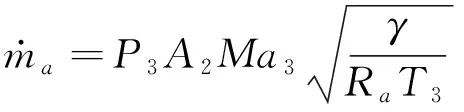
(5)
式中:qin为燃烧室内增加的热量;cp为氢气定压比热容;ηc为燃烧效率;LHV为氢气低发热值;fst为氢气理论化学当量比。
为简化起见,本文引用文献[8]给出的燃烧效率与燃油当量比的简单函数关系进行计算。T04,T03为总温,P04,P03为总压,存在以下关系:
(6)

(7)
在A3~Ae段,同样利用连续方程可以得到发动机出口处的气体参数Mae,Te,Pe,则发动机的推力为:
(8)
当Ma0=10时,得到推力随α和ψ的变化曲线如图5所示。采用拟合方法即可得到推力关于Ma0,α,ψ的解析表达式。

图5 推力随α和ψ的变化曲线Fig.5 Change of thrust with α and ψ
4 弹性模型
如图6所示,可以将飞行器看成两个固定于重心处的悬臂梁模型,忽略扭转变形和沿x轴方向的伸缩变形,只考虑弯曲变形,由于变形位移较小,故满足胡克定律。
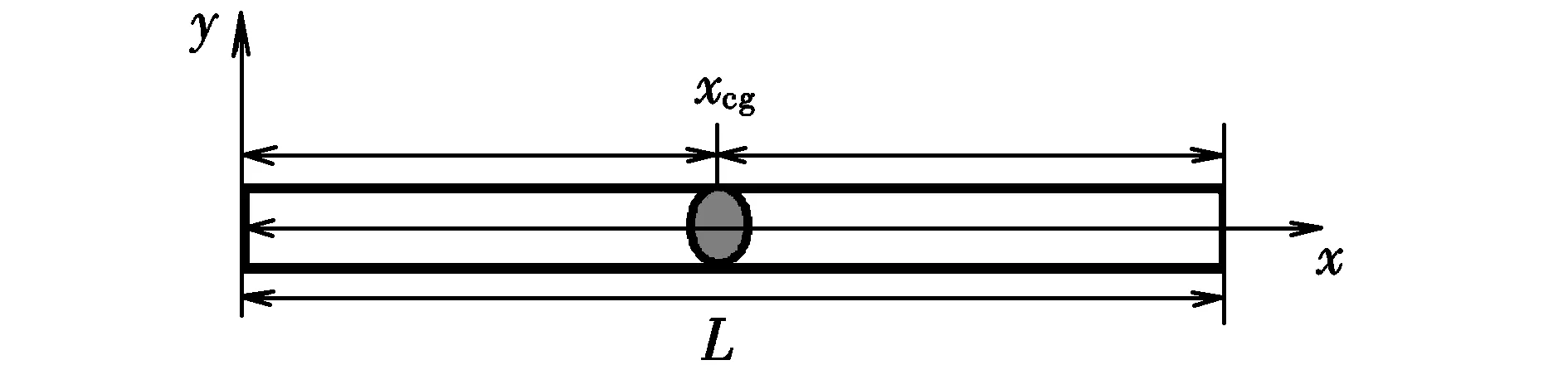
图6 HSV弹性模型Fig.6 HSV aeroelastic model
弯曲振动微分方程为:
(9)

φf,k(x)=
(10)
φa,k(x)=
(11)
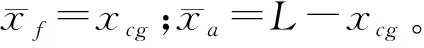
(12)


(13)
式(13)有无限多组解βk,前几组解如下:
βkx=1.875 1, 4.694 1, 7.854 8, 10.995 5,…
整个梁的一阶模态及其导数变化如图7所示。
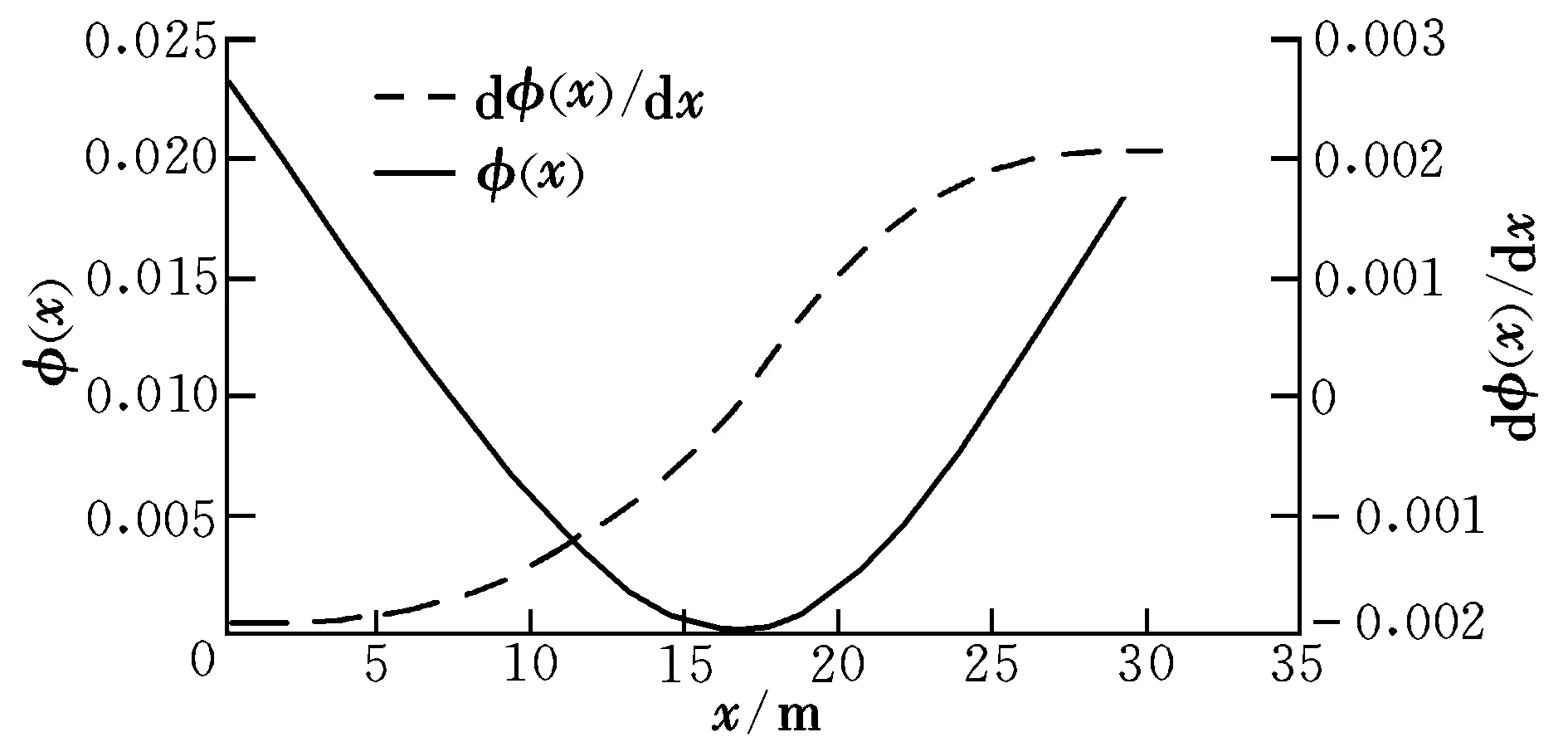
图7 一阶模态曲线及其导数Fig.7 First order mode curve and its derivatives
当梁受到分布力和集中力作用时,式(9)变为:
P(x,t)+Fj(t)δ(x-xj)
(14)
上式的解可以表示为:
(15)
式中:ηk(t)为广义坐标,满足以下方程:
(16)
式中:Nk(t)为k阶模态广义力。整个飞行器受到的集中力有升降舵产生的Fe和前部鸭舵产生的Fc。为了简化,直接将以上用工程算法得到的压力分布作为弹性机身的压力分布:
(17)
对于前部梁,广义力可以表示为:
(18)
对于后部梁,广义力可以表示为;
(19)
当Ma0=10,δe=δc=0,ψ=0.4 rad时,得到机体前部广义力Nf,1和机体后部广义力Na,1随迎角的变化如图8所示。由于飞行器几何参数有差异,本文增加了鸭舵,并且文献[7]给出的是简化解析拟合式,因此曲线有一定的差异,但是在走势上是一致的,结果具有一定的可信度。

图8 广义力随迎角变化曲线Fig.8 Change of generalized force with AOA
5 非线性动态特性分析
对于非线性系统可用以下方程来描述:
(20)
在标准分支分析方法中,x为n维状态变量,μ为可变控制参数,λ为m维固定控制参数,通过连续的改变μ即可求得系统的平衡曲线图。而实际情况中往往需要多个控制参数的协调配合才能够达到约束飞行的条件,此时就需要运用扩展分支分析方法才能达到目的。扩展分支分析方法通常分为两步。首先用标准分支分析方法求解:

(21)
式中:g(x)为k维约束方程(k (22) 然后采用标准分支分析方法再次计算式(22),即可得到约束条件下的非线性动力学特性。 在高超声速飞行器纵向刚体-弹性动力学模型[3]中,令: (23) 则飞行器纵向刚体-弹性动力学模型转化为: (24a) (24b) (25) 图9 控制舵对应关系Fig.9 Control surface schedule 从图9可以看到,存在两条平衡曲线,δc(δe)不满足一一对应关系,此时需要将这两条曲线分离,分别建立δc(δe)关系,然后代入式(22)再次分别利用常规分支分析方法进行平衡状态的求解。 计算过程中保持飞行高度不变,重心xcg=0.55l。将所有计算结果汇总得到V,α,ηf和ηa随升降舵δe变化的平衡曲线,如图10所示。因为本文对Ma0,α,δe,δc的取值有范围限制,范围之外的平衡解在图10中没有显示。 图10 V, α, ηf和ηa随δe变化的平衡曲线Fig.10 Changes of V, α, ηf and ηa with δe 图11 偏导数随迎角变化曲线Fig.11 Change of partial derivative with AOA 由于弹性的存在,当机身受到气动力的作用会发生弯曲,引起的迎角变化[9]可近似表示为: (26) 令ω(x,t)=φ(x)η(t),则式(26)可以转化为: (27) 由图10可知,在x=0和x=l弹性引起的迎角变化最大,利用上面求得的所有平衡状态可以得到飞行器处于巡航平衡状态时机体前端由于弹性引起的迎角变化最大值Δαf,max=0.109 2°,机体尾部由于弹性引起的迎角变化最大值Δαa,max=0.120 8°。 本文对具有典型乘波体结构的吸气式高超声速飞行器纵向进行了相关分析,得到以下结论: (1)针对高空巡航状态,利用扩展分支分析方法,得到了系统的分支图。分析发现该飞行器所有的平衡状态均是不稳定的,这主要是由于飞行器重心位于压心之前引起的。为了实现稳定,需要进一步利用相关控制方法来实现。 (2)根据本文建立的弹性模型,当该飞行器处于高空巡航平衡状态时,由于二维机身弹性引起的迎角变化较小,在初步进行分析时可以不考虑弹性对系统的影响。 参考文献: [1] 唐硕,祝强军.吸气式高超声速飞行器动力学建模研究进展[J].力学进展,2011,41(2):187-200. [2] Chavez F,Schmidt D.Analytical aeropropulsive/aeroelastic hypersonic-vehicle model with dynamic analysis[J].Journal of Guidance,Control,and Dynamics,1994,17(6):1308-1319. [3] Bolender M A,Doman D B.A non-linear model for the longitudinal dynamics of a hypersonic air-breathing vehicle[C]//Guidance,Navigation,and Control Conference and Exhibit.San Francisco,California,2005. [4] Clark A,Chivey Wu,Mirmirani M,et al.Development of an airframe-propulsion integrated generic hypersonic vehicle model[C]//AIAA Aerospace Sciences Meeting and Exhibit.Reno,Nevada,2006. [5] Mehra R K,Kessel W C,Carroll J V.Global stability and control analysis of aircraft at high angle of attack[R].AD A051-850,1977. [6] Ananthkrishnan N,Sinha N K.Level flight trim and stability analysis using an extended bifurcation and continuation procedure [J].Journal of Guidance,Control,and Dynamics,2001,24(6):1225-1228. [7] Jason T P,Andrea S,Stephen Y,et al.Control-oriented modeling of an air-breathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics, 2007,30(3):856-869. [8] 姚照辉.考虑飞/推耦合特性的超然冲压发动机控制方法研究[D].哈尔滨:哈尔滨工业大学,2010. [9] Clark A D,Mirmirani M D,Chivey W,et al.An aero-propulsion integrated elastic model of a generic airbreathing hypersonic vehicle[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit.Keystone,Colorado,2006.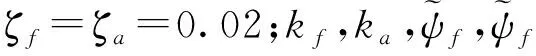
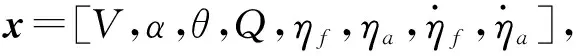




6 结论

