光栅刻划机刻划系统光机电集成优化方法研究*

申 远，王俊杰，竺长安，齐向东

(1. 中国科学技术大学 精密机械与精密仪器系, 安徽 合肥 230027; 2. 合肥师范学院 电子信息工程学院,安徽 合肥 230601; 3. 中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033)

光栅制造技术作为当今最为精密的技术之一，使得光栅刻划机被称为“精密机械之王”[1]. 光栅刻划机制造的光栅质量保证主要依靠两个方面：一是固定待刻光栅毛坯的分度系统的定位精度；二是刻划系统的刻划直线度.两方面的精度都需要同时保证，缺一不可.国内外的光栅刻划机研究，集中于分度机构的定位控制[2-3]，但刻划系统的误差控制对刻线直线性的保证非常关键，且无法采取补偿控制，仅仅依靠加工精度来保证十分困难.对于机械结构优化，虽然国内外也有大量研究，提出了众多的方法[4-6]，但是对于光栅刻划机这种大行程的超精密加工装置效果均不好.由于光栅刻线的长度达到400 mm，其精度又在纳米级，很难有设备能同时保证如此大范围的观察又具备纳米级的分辨率，如果用电子显微镜观察纳米级的刻线细节，又无法顾全整条刻线的直线度，因此刻划系统导致的误差形式也无法确定，这样就对刻划系统的结构优化带来了巨大的困难.

本文提出了光机电集成优化方法，利用计算傅里叶光学和光栅成像原理进行刻线误差分析，结合虚拟样机仿真和振动实验测量，确定了刀架导轨的振动情况以及对刻线的影响方式，然后基于此对刀架导轨的结构及参数进行优化，将该优化结果在中科院长春光机所的某型光栅刻划机上进行验证，达到了良好的效果.

1 刻划系统结构及光机电集成优化方法

光栅刻划机的刻划系统结构(见图1)，由复合式刀架、刀架导轨、凸轮等速机构和伺服电机组成．该系统的功能是实现刀具往复运动并完成光栅的刻划，本次对刻划系统的结构优化主要针对刀架导轨.

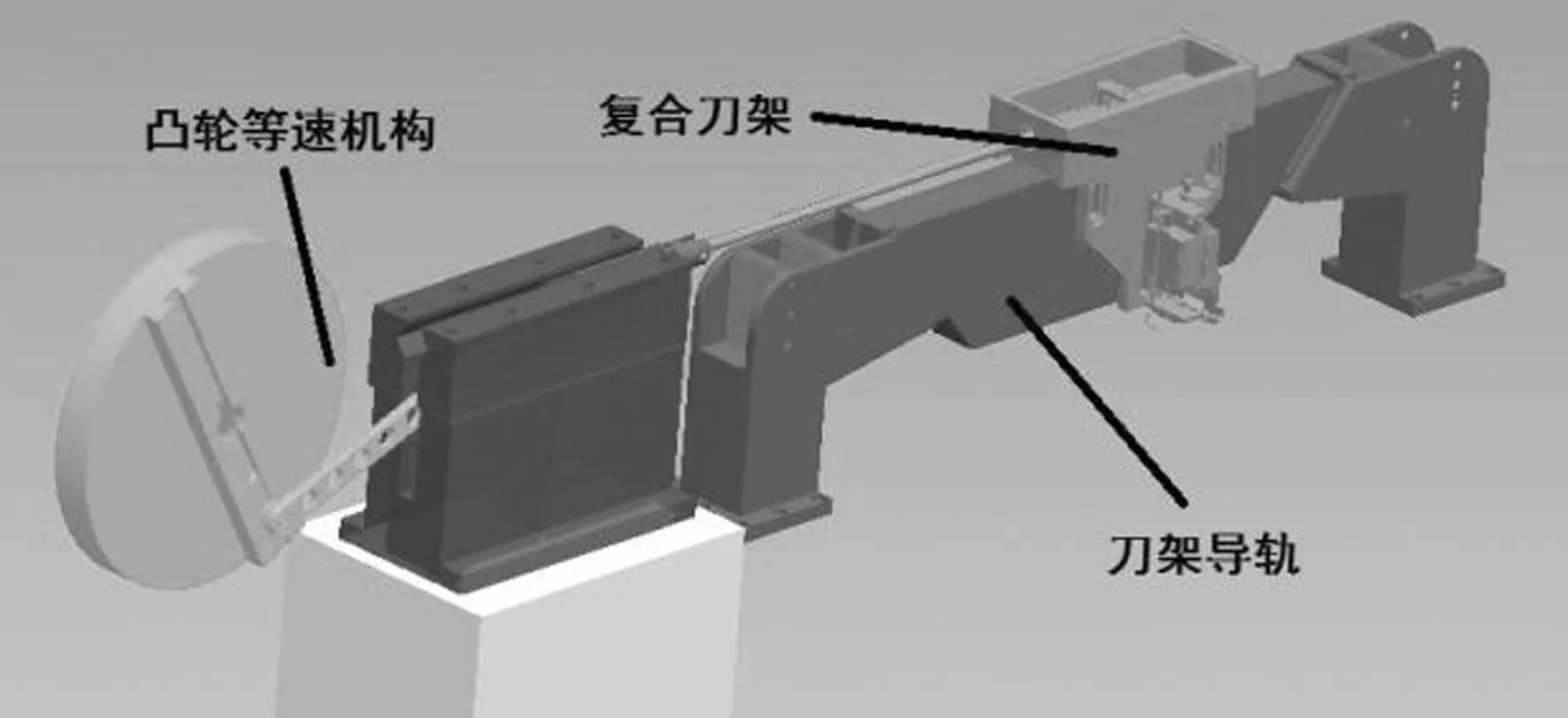
图1 刻划系统结构图

由于光栅刻划机是一个典型的光机电一体化精密仪器，采用常规方法对其刻划系统进行结构优化的可行性低且效果较差，因此提出在进行光栅刻划机结构优化的时候结合光学分析和实验测量进行集成优化，总体的流程如图2所示．

图2 光机电集成优化流程图

2 基于计算傅里叶光学的光栅刻线分析

由于光栅刻线的直接检测十分困难，所以一般采用光学手段，将刻线转化为衍射图、衍射波前来进行刻线质量的分析，光学测量采集的衍射图和衍射波前图判断完全依赖经验，因此对光栅刻线误差的精确分析带来了困难.鉴于此，采用计算傅里叶光学精确推算出具有不同误差形式的光栅刻线对应的衍射图以及衍射波前，然后将光学测量获得的衍射图像进行比对，就可以确定检测的目标刻线存在的误差是哪种形式，进而确定刻划系统的振动问题所在.

计算傅里叶光学是一种标量衍射理论[7].光波的传播行为是由最基本的麦克斯韦方程决定的，它是光电磁波的电场和磁场之间的一组耦合关系，由于它们之间的耦合，使得直接应用它求解是很难的.所以人们做了一些假设来简化求解的模型，如要求光波传播的电解质是线性、各向同性、介电常数均匀、非发散(介电常数与波长无关)、无磁化(磁导率等于真空中的磁导率)等，在这些条件下，可以解耦麦克斯韦方程，使得电、磁场可以独立地表达出来，而标量衍射理论指的就是在这些理想情况下光波的传播行为.

考虑单色光从一个2D平面(源平面)向接受面传播，如图3所示，那么接受面上的光强分布可以由瑞利-菲尔德衍射公式求解[8]，即：

(1)

图3 单色光传播示意图

式(1)相当于惠更斯-菲涅尔准则，这个准则假设源平面由无限个假想的源点组成，每一个都产生球面波向前传播，这些球面波在接受面上的各点进行干涉叠加，从而得到接受面的成像.

一般光栅衍射都属于远场衍射，因此采用夫琅禾费近似，夫琅禾费衍射表达式为式(2)：

(2)

根据以上的计算傅里叶光学理论，使用Matlab编写了光栅成像的程序，计算各种光栅刻线和理想光栅刻线的衍射图、衍射波前、光强分布，如图4所示，然后整理成数据库，便于通过测量获得的衍射图像判断光栅刻线的误差形式.

图4 理想光栅刻线的衍射图、衍射波前

对光栅刻划机刻划出的光栅刻线进行光学检测，获取其衍射波前后与数据库比对，确定了光栅刻线误差形式为C型弯曲，如图5所示．

图5 实测光栅刻线对比图

3 虚拟样机仿真以及样机实验测量

在建立虚拟样机的基础上，采用基于Pro/E的虚拟样机仿真分析结合的方法对刀架导轨的振动特性进行分析，以找到刀架导轨振动的作用机理和影响程度，分析确定刀架导轨的振动频率、最大振动幅值及其对刻刀轨迹直线度的影响.

采用Pro/E中的Mechanical模块对刀架导轨进行有限元模态分析,设置刀架导轨的虚拟样机模型如下: 刀架导轨材料为石英玻璃，两边底座为HT200，其他部件为45刚，约束为底座固支，具体如图6所示.

图6 刀架导轨仿真分析图

从有限元模态分析计算的结果来看，刀架的导轨固有频率除了一阶在399.62 Hz外，其他均在700 Hz以上.由于刻划运动周期一般在10 s左右，基本排除了引发共振的可能.

在虚拟样机的仿真分析后，又对实际样机进行了振动实验，图7为对刻划系统进行振动实验的方案，采用激光干涉仪对刀架导轨的中点以及左、右1/4处进行了刻划运动中的定位测量.本系统中使用分辨率可以达到0.15 nm的双频激光干涉仪，保证测量的高精度.

图7 刀架导轨振动实验方案

激光干涉仪测量的结果数据如图8(a)，表示的是刀架导轨上3个测量点在垂直于刻划方向上的位移.

对测量数据进行了分析，傅里叶分析的结果如图8(b)所示，可以明显看出，刀架导轨是按照系统的刻划周期10 s发生震动，即0.1 Hz的刻划频率.考虑到刻线实际就是刀头的轨迹，即刻线轨迹.分别得到刀架导轨的近似振动方程和刀架的理论运动方程后，再通过将两个位移量进行拟合，得到光栅刻线的轨迹.

图8 刀架导轨振动实验结果

从测量获得的数据已知,刀架导轨的振动曲线近似弦型，则可以将其振动简化为一个弦的振动，而弦上的每一点又在其振动方向上符合简谐振动.根据振动理论[9]，可以得到弦上的坐标为x的点的振动幅值方程为：

y1=sin(xπ/l)．

(3)

通过对刀架导轨的振动数据分析，其振动周期为10.05 s，在假设的弦上某一点的简谐振动方程为：

y2=sin(2πt/10.05)，

(4)

则刀架导轨上各点的振动方程为：

y=y1y2=sin(xπ/250)sin(2πt/10.05)．

(5)

刀架位移方程：

上文中已经得出刀架的运动方程为式(6)：

(6)

由于在分析中考虑到将刀架位于最尽端时的坐标定位x轴起始坐标，通过坐标转换可得到其新的运动方程为：

(7)

式中：θ为曲柄转过的角度，θ=πt/5．

根据曲柄滑块的结构，曲柄的长度为a=125，连杆的长度为b=350，将其代入到式(7)，得到曲柄滑块的位移方程为：

125cos(πt/5)-225(8)．

(8)

最后获得了刻刀的轨迹方程为式(9)：

(9)

轨迹方程绘制出来如图9所示，证明也是C型的弯曲刻线，与计算傅里叶光学误差分析以及刻划系统实验的结果一致，极有可能为刀架的周期性运动产生的激振(从数据的频率上看)，确定误差后，结构优化的目标即为减小该振动的振幅.

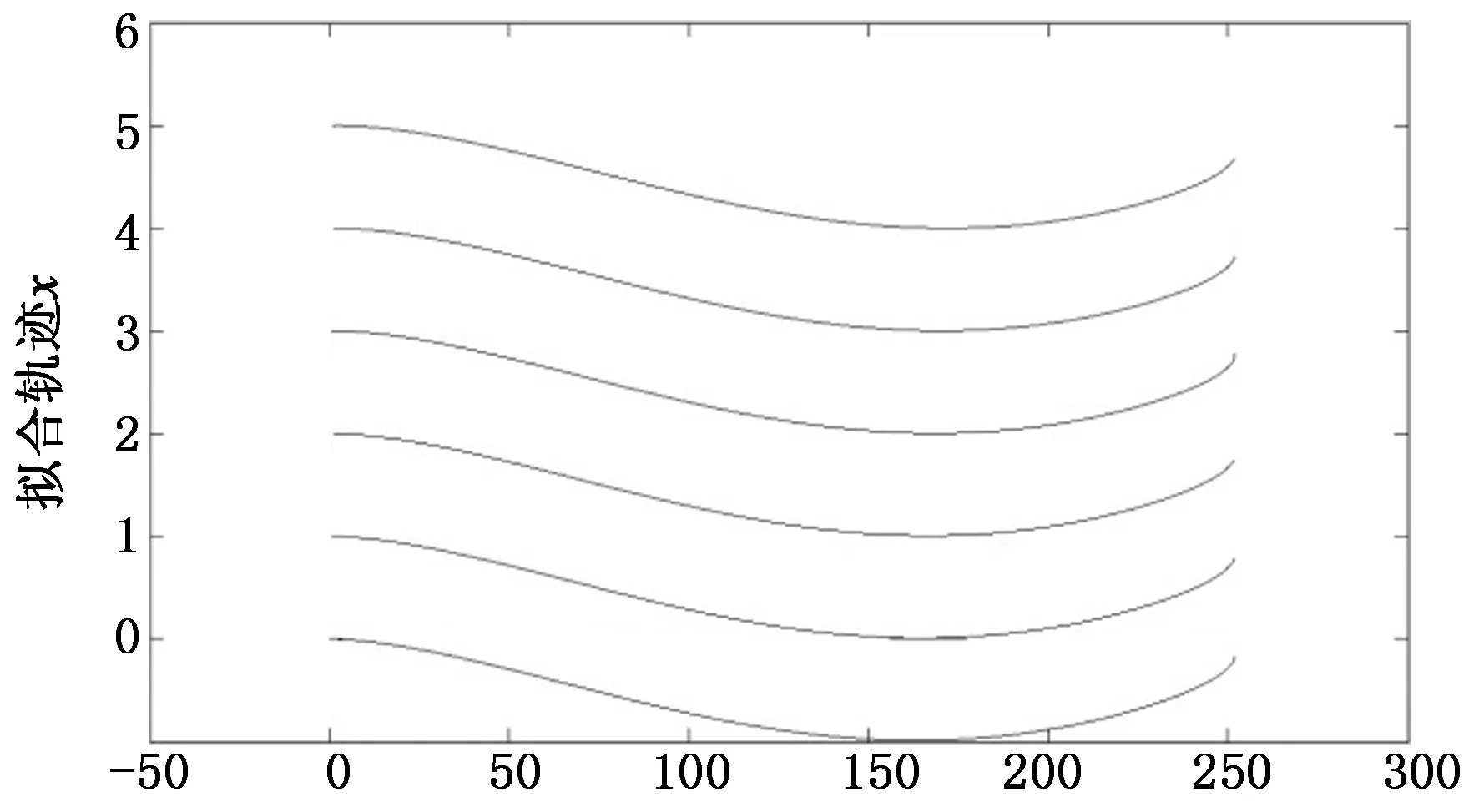
拟合轨迹y

4 基于Pro/Toolkit的智能优化方法

通过多种优化方案的对比和分析，确定在刀架导轨的两侧添加支撑性的加强筋来实现刀架导轨的结构优化.对无支撑结构和有支撑结构进行振动模态分析，对比其整个导轨上的振幅情况.

对比有支撑结构的振幅曲线发现，无支撑结构的最大振幅值在0.998 mm，而有支撑结构的最大振幅值为0.842 mm，振幅减少了15.6%，结构优化的效果良好.经过反复的参数敏感度分析，确定了对振幅敏感的参数是前支撑结构与刀架导轨边缘的距离，后刀架导轨由于分度系统的存在，无法改变参数，因此对前支撑结构与刀架导轨边缘的距离参数d进行优化.

刀架导轨位置/mm

刀架导轨位置/mm

由于对参数d进行优化需要进行多次CAE分析以及结果分析获得最优值，采用Pro/Engineer的二次开发接口Pro/Toolkit来进行智能化参数优化[10].

Pro/Toolkit可以让用户以编程方式实现自己所需要的特定功能，编写了如图13的优化流程，其最优参数的求解采用了基于遗传算法的最优解搜索[11]，实现了参数d的最优化求解.

图12 敏感参数示意图

图13 智能优化流程

考虑到装配和工艺的因素，d参数的取值范围在30～160 mm之间，经过智能优化程序的优化后，获得的最优参数值为142 mm.由上图可知优化后振幅变为了0.706 mm，和优化前的0.842 mm相比又减小了16.1%，优化效果明显.在振幅减小的情况下，光栅刻线的直线度和质量也有较大的提高.

5 结论和展望

针对光栅刻划机在宏观尺度下进行微纳加工的工作特点，提出了一种光机电集成优化方法．利用计算傅里叶光学和光栅成像等原理进行刻线误差分析，结合虚拟样机仿真和实际振动实验测量，确定了引起光栅刻线误差的振动方式，并基于此对刀架导轨的结构及参数进行了智能优化研究．仿真结果表明，将刀桥的振动幅度减小了30%，达到了良好的效果，提高了光栅刻线的直线性和质量，也验证了该集成优化方法的可行性.

下一步研究工作:进一步将该优化方法进行有机集成，形成一套成熟的优化设计体系，使其适用于各型号光栅刻划机以至于其他同类型光学精密仪器.

[1] 时轮, 郝德阜, 齐向东. 高精度的光电式衍射光栅刻划机[J]. 仪器仪表学报, 2001, 22(S2) : 103-104.

SHI Lun, HAO De-fu, QI Xiang-dong. High precision photoelectric diffraction grating ruling engine[J].Chinese Journal of Scientific Instrument, 2001, 22(S2):103-104.(In Chinese)

[2] LU Li-hua, LIANG Ying-chun, GUO Yong-feng,etal.Design and testing of a nanometer positioning system [J]. ASME Journal of Dyn Syst Meas Control, 2010, 132(2):021011.

[3] 张金龙, 刘阳, 郭怡倩,等. 纳米级超精密定位工作台的研究[J]．机械工程学报,2011,47(9): 187-192.

ZHANG Jin-long, LIU Yang, GUO Yi-qian,etal.Research on ultra-precision nanopositioning stage[J].Chinese Journal of Mechanical Engineering, 2011,47(9): 187-192.(In Chinese)

[4] 刘灿昌,裘进浩,孙慧玉,等．悬臂梁智能结构主共振响应的最优化控制[J]． 中国机械工程, 2013,24(12): 1600-1604.

LIU Can-chang, QIU Jin-hao, SUN Hui-yu,etal. Optimal control of primary resonance of smart structures of cantilever beams[J]． China Mechanical Engineering, 2013,24(12): 1600-1604.(In Chinese)

[5] XU Bin, CHEN Nan, CHE Hua-jun. An integrated method of multi-objective optimization for complex mechanical structure[J]. Advances in Engineering Software, 2010,41:277-285.

[6] 洪亚军, 曹岩枫, 尹强,等.火炮身管反后坐装置集成优化设计方法研究[J].中国机械工程, 2013,24(1):15-20.

HONG Ya-jun, CAO Yan-feng, YIN Qiang,etal.Research on integrated optimization method of barrel and recoil mechanisms[J]. China Mechanical Engineering, 2013, 24(1): 15-20.(In Chinese)

[7] VOELZ DAVID. Computational fourier optics[M]. SPIE Press, 2011.

[8] 谢敬辉,赵达尊,阎吉祥,等. 物理光学教程[M ]. 北京:北京理工大学出版社, 2005.

XIE Jing-hui, ZHAO Da-zun, YAN Ji-xiang,etal. Physical Optics[M]. Beijing:Beijing Institute of Technology Press, 2005.(In Chinese)

[9] 张宏志,宋超,张晓峰,等.琴弦振动理论在工程中柔索求拉力的应用[J]. 振动与冲击, 2002,21(3):77-78.

ZHANG Hong-zhi, SONG Chao, ZHANG Xiao-feng,etal. Application of the chord vibration theory to solve the tensile force of flexible cable in engineering[J]. Chinese Journal of Vibration and Shock, 2002,21(3):77-78.(In Chinese)

[10]魏珅,钟小强,陈开,等.基于Pro/Toolkit的锻压机床装配模型快速设计[J]. 计算机工程, 2008, 32(21):239-241.

WEI Shen, ZHONG Xiao-qiang, CHEN Kai,etal. Rapid design of metalforming machines’ assembly medel based on pro/Toolkit[J].Computer Engineering, 2008, 32(21):239-241.(In Chinese)

[11]李智勇，陈友文. 一种融入小生境技术的遗传禁忌算法[J].湖南大学学报:自然科学版, 2010, 37(4):81-84.

LI Zhi-yong,CHEN You-wen.A hybrid strategy based on genetic algorithm and tabu search importing niches[J].Journal of Hunan University:Natural Sciences, 2010, 37(4):81-84.(In Chinese)