基于支持向量机的地铁客流量预测

赵钰棠 杨信丰 杨 珂

(1.兰州交通大学交通运输学院 兰州 730070;2.北京城建设计发展集团股份有限公司 北京 100037)

基于支持向量机的地铁客流量预测

赵钰棠1杨信丰1杨 珂2

(1.兰州交通大学交通运输学院 兰州 730070;2.北京城建设计发展集团股份有限公司 北京 100037)

地铁客流量是城市地铁交通运营组织的重要依据，客流随机性较大，其影响因素较多，因此加大了客流预测的难度。为了更加准确地预测城市地铁交通中的客流量，及时对客流组织方案进行调整，设计了一种基于非线性支持向量回归机的地铁客流量预测方法。该方法通过分析已采集数据的影响因素，确定对客流量影响较大的支持向量，然后构建预测模型进行预测。该模型可以通过调整影响因素的强度来提高预测精度。最后，通过算例验证:该方法可以有效地改善预测误差，适用于短期和不确定环境的地铁客流预测。

地铁;支持向量机;地铁客流量;预测;影响因素

在城市地铁交通中，若能准确地预测各车站的交通流量信息，就可以在此基础上制定合理的运营方案，使运能与客流需求相匹配，降低车厢拥挤程度，同时又可避免列车满载率过低、运能浪费［1］，并且可以适当调整车站设备的运行状态，使方案具有最佳经济效益和社会效益。

地铁客流预测的方法有很多种，传统的预测方法有回归分析算法以及Kalman滤波等［2］，这些方法都假设系统为平稳的线性系统，因此在线性系统平稳的预测中能够得到满意的结果。但是，地铁交通是有人参与的主动系统，具有非线性和扰动性强的特征，很难有特定的函数表达形式，因此用以上方法难以获得很好的效果［3］。

支持向量机是数据挖掘中的一项新技术，随着近些年来相关研究的深入，支持向量机被更多的人所认识，很多人将其应用于公路道路车流、客流的预测中，但在地铁客流预测中的应用还很少，有的只是将其简单应用于下一年、下一天的客流预测，并没有将日期、天气等影响因素考虑进去预测各时间段的客流量［4］。

本文利用地铁扶梯客流的统计数据，考虑到外部的一些影响因素，借助支持向量机方法，使用LIBSVM工具箱对人流的特征向量进行学习训练，经过交叉验证确定最优参数，并通过预测数据与原始数据对比来验证预测的准确性，为地铁客流量预测提供一种新思路。

1 非线性支持向量回归机(SVMR)

支持向量机(SVM)是Corinna Cortes和Vapnik于1995年提出的，它建立在VC维和结构化经验风险最小化原理的基础上，是一个凸二次优化问题，可以在模型的复杂性和学习能力之间寻求最佳折中，SVM避免了人工神经网络常出现的“过学习”问题，可以解决小样本、非线性、高维的实际问题，具有良好的推广性［5］。

支持向量机通过内积函数(即核函数)定义的非线性变换将输入空间变换到一个高维空间，并在这个空间中求最优分类面。最优分类面要求分类线不但能将两类正确分开，而且可使分类间隔最大，离分类线最近的向量被称为支持向量［5］。

支持向量机分为分类机和回归机，回归问题与分类问题结构相同，但它们的输出和取值范围不同，通过一个非线性映射核φ将数据映射到高维特征空间，并在这个空间进行线性回归，高维空间的线性回归对应于低维输入空间的非线性回归，找到一条训练点偏离最小的直线，构造决策函数。

给定训练集 T={(x1，y1)，…，(xl，yl)}∈(Rny)，其中 xi∈Rn，yi∈y=R，i=1，…，l，(在本文案例中有 5 个输入，分别为 x1，x2，x3，x4和 x5)。选取适当的从空间 Rn到高维空间的变换φ:x=φ(x)、精度ε＞0和惩罚参数C＞0，非线性支持向量回归机可以通过求解来实现［6］，有

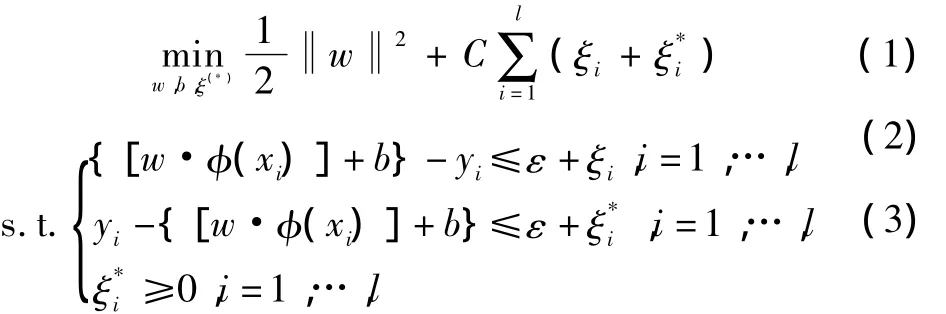
通过引入Lagrange函数，将原始问题化为它的对偶问题［6］

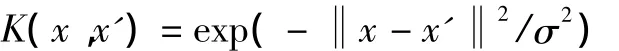
2 支持向量回归机对地铁客流的预测

2.1 确定影响因素

影响地铁客流量的因素有很多种，短期影响因素主要体现在天气、周末、节假日、突发事件以及出行目的等;长期影响因素主要体现在地面公交对地铁客流的竞争，政府导向、票价以及居民收入等。在一般的预测当中，短期影响因素比长期影响因素更为多变、时效性强，因此选择短期因素作为主要影响因素。

短期影响因素选取的主要依据在于:在恶劣天气状况下，客流的集中性较强，总体客流数量会因天气恶劣程度的加重而下降;周末早晚高峰的客流量明显低于工作日，每个时间段的出行人数较为平缓;在节假日，尤其在一些景点附近，旅游的客流量大幅度增加;当有突发事件发生时，事发地点的客流量会急剧升高，事件结束后又会逐渐减少;在某一固定区域，大部分人的出行目的较为规律，小部分人的出行随机性强，调查困难，故可以将其假定为一个固定值。在计算时根据影响因素的强弱，优先选择影响力大的因素，过多因素的选取虽然可以提高预测精度，但是也会导致计算繁琐、耗时增加。故本文选取以下4项影响因素:

1)周末。如果是周末，影响值定义为1，否则为0。

2)天气。通过查阅历史天气，确定每周的天气状况，按照天气状况确定影响值，例如晴天取1，阴天取0.5，大雨、大雪天取0，其他情况折中取值。

3)节假日。按照不同节假日影响程度的不同确定影响值，例如根据客流情况可以确定无节假日为0，五一期间为 0.5，十一期间为 0.7，春节 期 间为 1［4］。

4)突发事件。如大型演唱会、运动会等，有则影响值为 1，否则为 0［4］。

2.2 数据预处理

以上海地铁莘庄地铁站1号口2011年4月9日到17日的客流统计作为客流数据，见表1［4］。地铁从早上5点开始运营，晚上23点结束运营，每天从5点到23点以1 h为单位作为客流样本，在数据中将其以标号1到18代替。4月15日和17日的数据作为测试样本，其他7 d的数据作为训练样本。

由于样本数据的评价标准不一样，需要对其量纲化，统一评价标准，提高预测精度。所以，对训练集和测试集进行归一化预处理，采用归一化映射

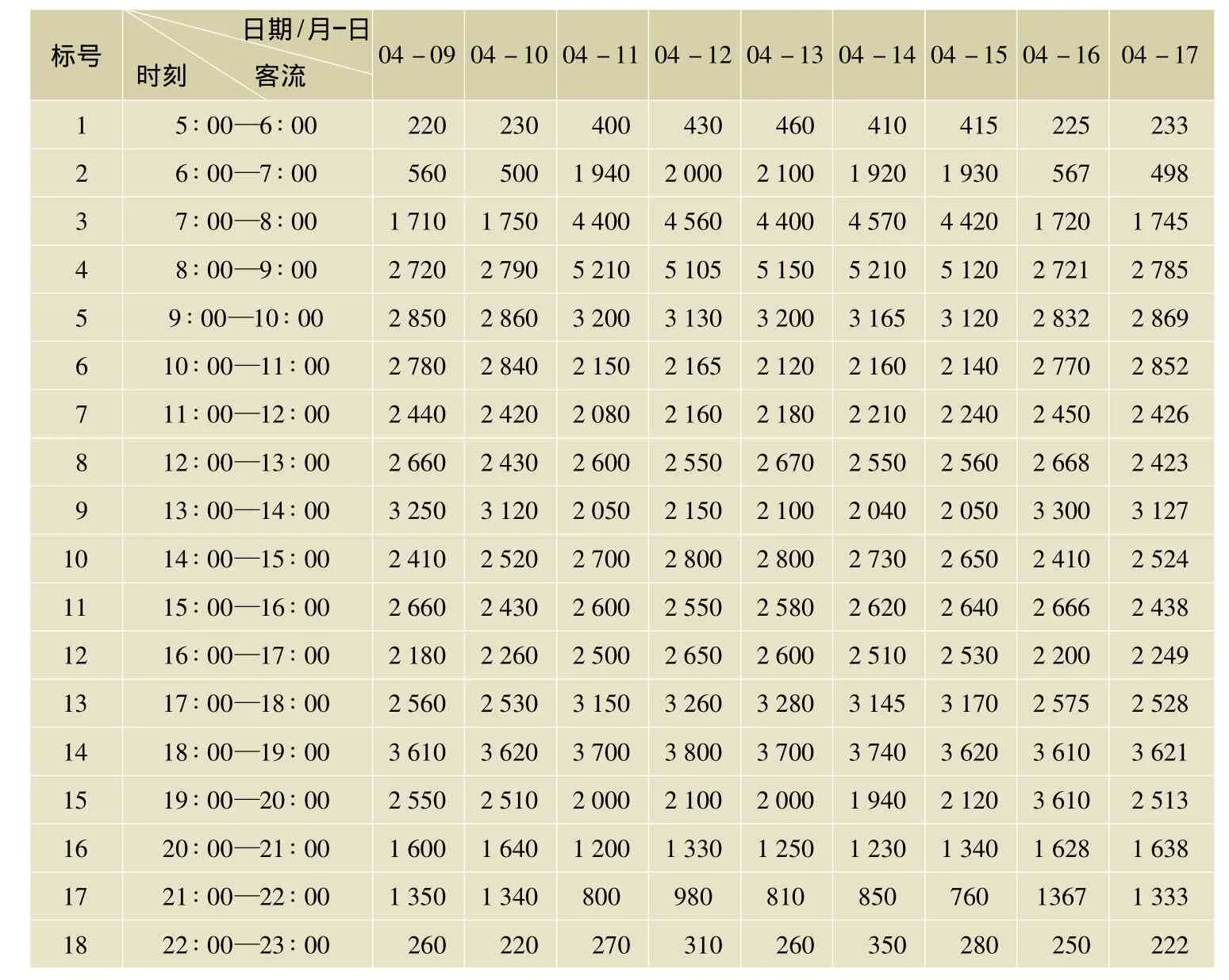
表1 2011年客流统计数据 人次

其中，x，y∈Rn，xmin=min(x)，xmax=max(x)，归一化的效果是原始数据被规整到［0，1］范围内，本文使用Matlab中的Mapminmax函数进行归一化和反归一化，在模型训练前将各组自变量及因变量分别进行归一化，然后使用归一化的数据对模型进行训练和预测，最后将预测后的数据进行反归一化，得到预测值。

2.3 模型建立

将时间标号和影响因素作为自变量，对应于训练集T的x变量，在本文案例中为5个输入。客流量作为因变量，对应于训练集T的y变量。对样本进行交叉验证，结果如表2所示。

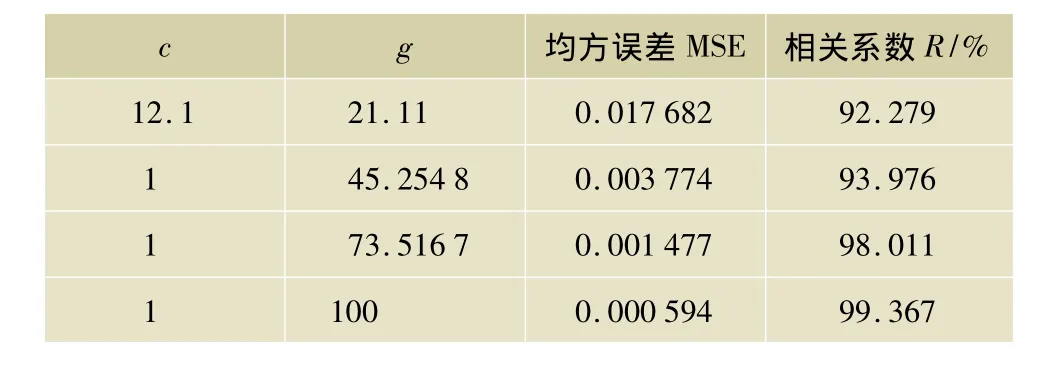
表2 参数c和g的选取

2.4 预测结果对比分析

使用模型对4月15日客流量进行预测，结果如表3及图1所示，得到非线性支持向量回归机的最大误差为14.33%，最小为0.04%，平均相对误差为4.77%。

使用模型对4月17日客流量进行预测，结果如表4及图2所示，得到非线性支持向量回归机的最大误差为21.62%，最小为 1.58%，平均相对误差为5.13%。

通过数据对比可知，4月15日(正常日)的预测结果要优于4月17日(周末)的预测结果，这是因为对于4月15日而言，对应的训练数据(正常日)为4组，而对于4月17日而言，对应的训练数据(周末)只有3组。因此，会导致预测15日客流的支持向量多于17日的支持向量。这说明，在一定范围内，训练数据的增加可以使模型涵盖更多种客流情况，提高预测精度。

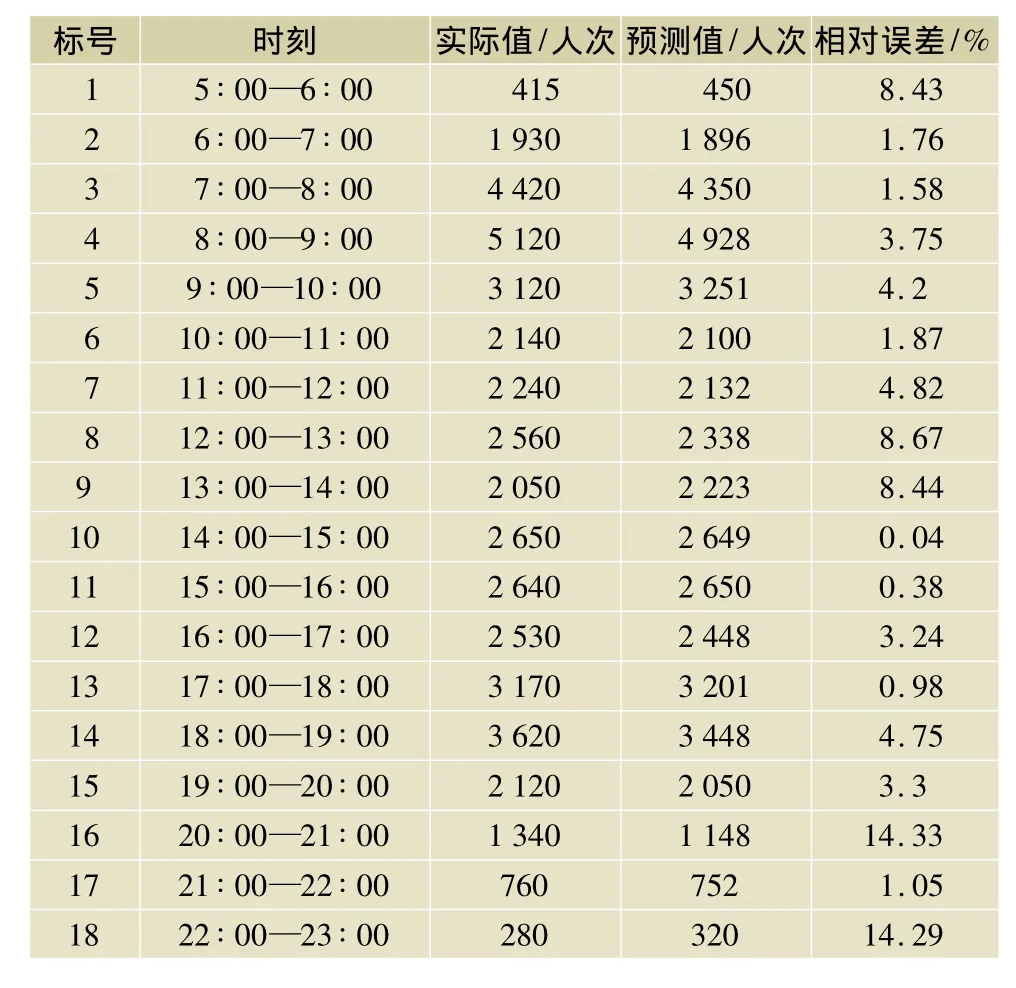
表3 2011年4月15日的预测结果对比

支持向量机对地铁客流预测的稳定性高，误差相对较小，相对于地铁站巨大的客流量和地铁客流随机性强的特点，非线性支持向量回归机的误差范围是可以接受的，因此用该方法预测地铁客流是可行的。根据预测数据，可以对行车组织计划进行相应的调整，动态调节地铁站自动扶梯的传动速度，提前做好高峰时段的准备工作，为地铁系统的高效运营提供保障。

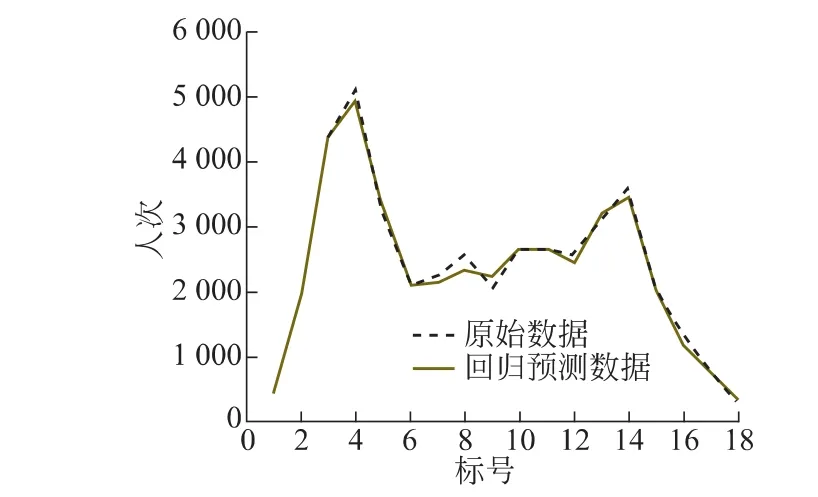
图1 2011年4月15日原始数据与预测数据对比

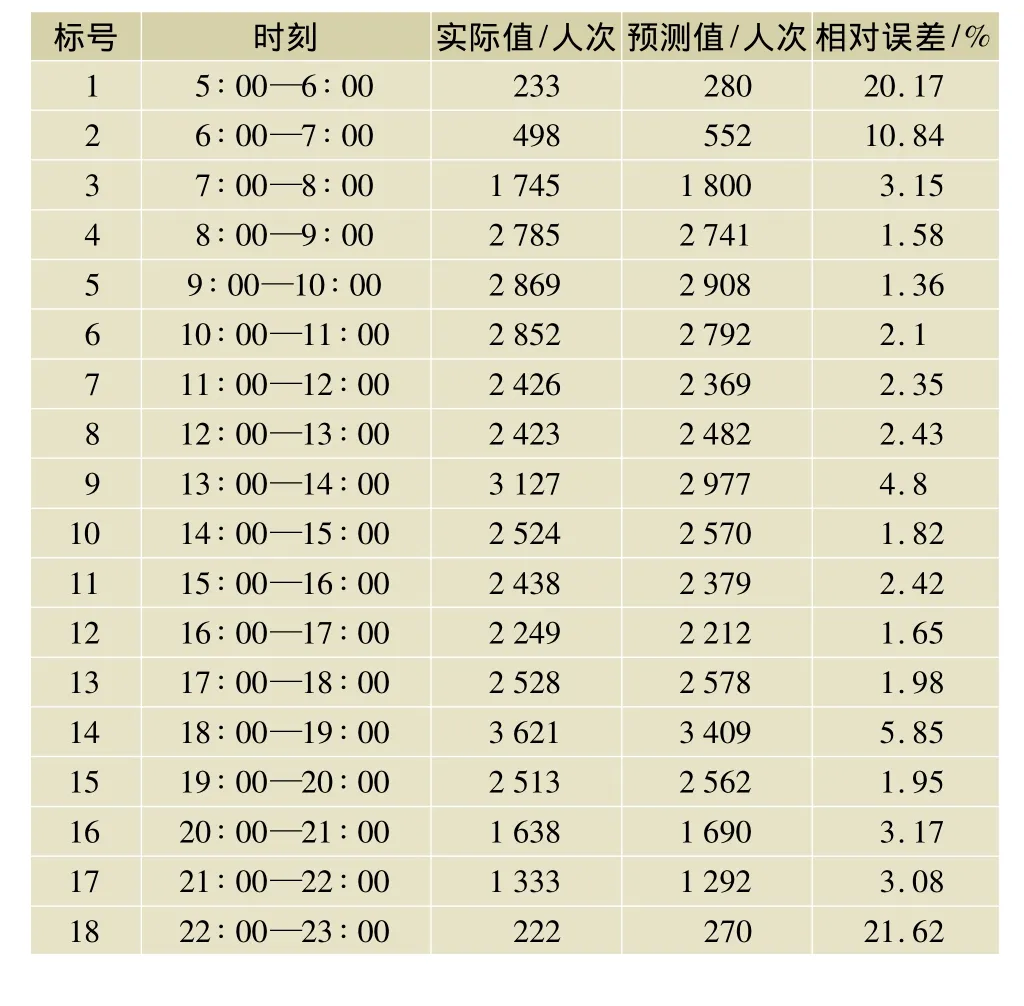
表4 2011年4月17日的预测结果对比

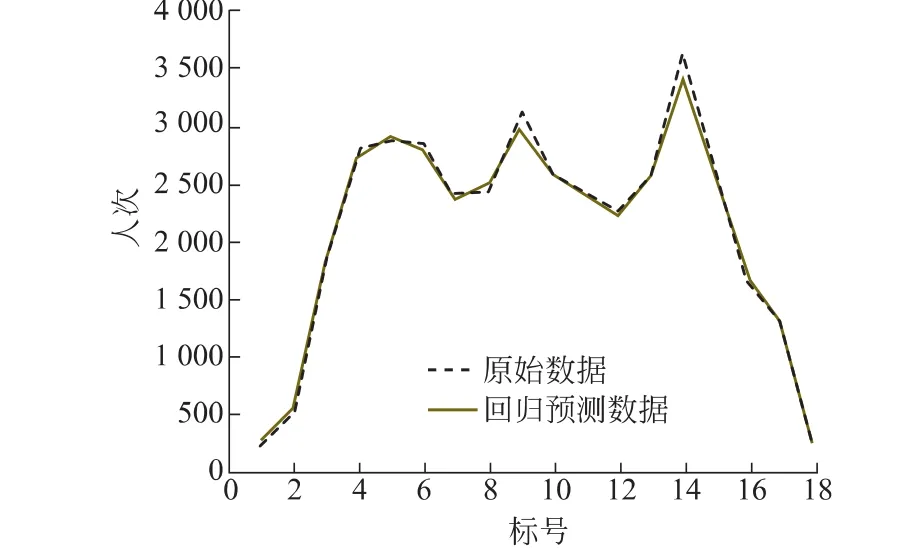
图2 2011年4月17日原始数据与预测数据对比

3 结论

利用地铁扶梯客流的统计数据，考虑到外部的一些影响因素，借助支持向量机，使用LIBSVM工具箱对人流的特征向量进行学习训练，经过交叉验证确定最优参数，并利用预测数据与原始数据对比来验证预测的准确性。经过验证得出:非线性支持向量机对地铁客流量的预测效果较好。由于在支持向量机中，少数支持向量决定了最终结果，可以剔除大量的冗余样本，算法简单，具有较好的鲁棒性。另外，支持向量机增、删非支持向量对模型没有影响，有些应用中对核的选取不敏感，从而在建立模型时，可以考虑更多的影响因素，使预测值更加接近真实值，因此该方法适用于短期和不确定环境的地铁客流预测。本文只使用9天的客流量数据进行训练，若能将其投入实际应用、不断地增加客流样本，就能获得大量的训练数据，支持向量机就可以得到更充分的训练，使得预测更加精准，从而更好地将其应用于客流组织。

［1］吴强，冯维琇，胡晓嘉.灰色预测法在城轨客流预测中的应用［J］.城市轨道交通研究，2004，3(7):52－54.

［2］李存军，邓红霞.基于数据融合的地铁客流量预测方法［J］.铁道学报，2004，1(26):116 －119.

［3］郭牧.孙占全.短时交通流预测方法研究［J］.计算机应用研究，2008，9(25):2676 －2678.

［4］鲁明旭，叶银忠，马向华.神经网络在地铁客流预测中的应用［J］.机械研究与应用，2012，3(25):86 －89.

［5］王定成.支持向量机建模预测与控制［M］.北京:气象出版社，2009:12 －27.

［6］邓乃扬，田英杰.支持向量机:理论、算法与拓展［M］.北京:科学出版社，2009:64 －96.

［7］史峰，郁磊，王小川，等.MATLAB神经网络30个案例分析［M］.北京:北京航空航天大学出版社，2010:112－140.

Subway Traffic Prediction Based on Support Vector Machine

Zhao Yutang1Yang Xinfeng1Yang Ke2
(1.School of Traffic＆ Transportation Engineering，Lanzhou Jiaotong University，Lanzhou 730070;2.Beijing Urban Construction Design＆Development Group Co.，Ltd.，Beijing 100037)

Abstract:Subway traffic is one of the main basic data for subway operation and organization. However, the prediction of subway traffic is difficult for its randomness and multi-influencing factors. In this paper, an improved method of data prediction based on Support Vector Machine (SVM) is proposed to obtain a more precise prediction for subway -stations traffic,which can be used for operation and organization of subway.This method can predict subway traffic by analyzing collected data and determining which support vectors have more impact on traffic, and then adjust the strength of influencing factors to improve prediction accuracy. Experimental results show that SVM can evidently decrease error and predict subway traffic in a short time and in uncertain environment.

Key words:Metro; Support Vector Machine (SVM); subway traffic; prediction; influencing factors

U293.13

A

1672－6073(2014)03－0035－04

10.3969/j.issn.1672 －6073.2014.03.009

收稿日期:2013－05－07

2013－07－01

作者简介:赵钰棠，男，硕士研究生，从事城市轨道交通运营管理研究，zhaoyutang345@163.com

杨信丰，男，副教授，硕士生导师

教育部人文社会科学研究项目(13XJC630017)

(编辑:郝京红)