基于多元非完备信息的实时滤波定轨方法

淡鹏, 李恒年, 张定波, 王丹

(1.西安卫星测控中心 宇航动力学国家重点实验室, 陕西 西安 710043;2.西安卫星测控中心 技术部, 陕西 西安 710043)

0 引言

基于扩频及统一S波段测控设备的外测测量数据是卫星实时轨道计算使用的一种重要观测数据。由于此类数据中的测距、测速、测角等信息在实际采集及传输过程中不在一帧数据中存在,从而给同时使用这些数据的实时滤波轨道确定计算带来一些问题,即需要先将此类数据通过时标的插值对齐及数据拼接,转换为信息完备的数据帧使用。而这种数据的插值对齐及拼帧操作不但增加了数据处理的复杂度,而且不可避免地带来精度损失,在对齐算法有缺陷时还会引起其他问题。因而,在实时滤波轨道计算中直接使用非完备观测数据成为提高计算精度的有效方法之一。文献[1]采用“当前”统计模型和UKF算法,给出了一种多测速系统实时定轨算法。文献[2]提出了一种基于扩展卡尔曼粒子滤波的仅测角卫星被动跟踪算法。文献[3]利用EKF原理,提出了一种单星仅测角滤波定轨跟踪算法。文献[4]联合了星间测距和测速数据,利用参数加权平差算法来提高星座定轨精度。文献[5]对定位与测速数据融合重建轨道方法进行了研究。但这些算法基本上是针对外测数据中固定的一种或几种观测信息的使用,没有将各种非完备观测数据综合利用。

本文在UKF算法和EKF算法研究的基础上,通过在计算过程中进行变维矩阵及向量运算的方法将各类非完备外测观测数据进行混合使用,并对其实现过程和使用效果进行了分析。

1 非完备外测数据观测模型

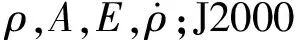
对测距、方位角、仰角、测速各测元值有:

即可将地心惯性系的运动状态向量转换到测站地平系下的测量量。

2 基于变维矩阵运算的非完备外测数据混合使用方法

2.1 实现思路

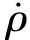
2.2 UKF滤波中的变维矩阵运算实现

UKF是一种使用采样策略近似函数非线性分布的递归贝叶斯估计算法[6]。该方法以采样变换为基础,采用卡尔曼滤波框架对数据点进行确定性采样,而不必直接对函数进行线性化处理,具有实现过程简单、避免了繁琐的雅可比矩阵求导、收敛速度较快、对噪声适应能力强等特点,是实时滤波轨道计算中使用较多的一种方法。

从UKF的算法步骤可看出,其计算过程主要为矩阵和向量运算,根据当前数据帧中状态值S可实现各步骤涉及的矩阵及向量的维数的动态调整。

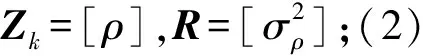
其他测元组合情况依次类推,由UKF计算公式可得,观测方差阵PZZ、增益矩阵Kk、状态向量与观测向量相关协方差阵PXZ也随之成为变维矩阵。

2.3 EKF滤波中的变维矩阵运算实现

EKF滤波是另一类广泛使用的非线性滤波器,它是对基本卡尔曼滤波的扩展和推广,通过对非线性函数的线性化近似处理来应用线性系统的卡尔曼滤波公式[7-8]。

从EKF算法步骤可知,设tk时刻数据帧中有效测元个数为nk,则通过设置测元的有效标志及变维向量及矩阵运算,在EKF滤波中进行非完备观测混合使用时,观测矩阵Hk需要根据当前帧各测元的有效标志进行变维处理,此时增益矩阵Kk、残差向量Yk、噪声协方差阵Rk等都需要根据nk进行变维。

2.4 各测元的野值判断及剔除

雷达测量数据中的野值[9-11]是影响滤波性能的重要因素,因而算法实现中必须考虑抗野值问题。对EKF与UKF两种滤波算法,野值的判断涉及到观测残差与观测协方差的运算问题。

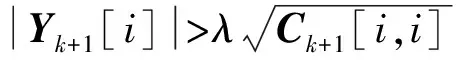
考虑到此种判断有一定的局限性,即不满足此条件的情况还可能是轨道发生机动或滤波出现异常;因此判断时可保存多点新息数据,综合该新息序列及测站跟踪历史数据的野值情况判断其是否有轨道机动发生(如采用连续多帧判断的方法)。

2.5 实现过程对比探讨

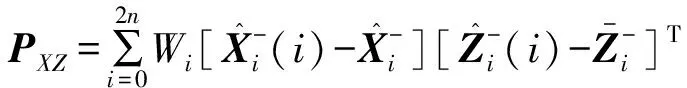
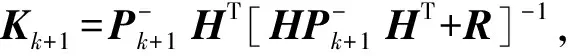
考虑到多站观测条件下,三站测距可几何法确定位置,三站测距测速可确定位置速度,因此,在不考虑各测站系统误差的情况下,当测元类型固定时,使用多站信息的滤波收敛性应优于单站情况。

对于测角信息,根据RAE到测站地平系转换公式ρx=ρcosEsinA,ρy=ρcosEcosA,ρz=sinA,当测距ρ较大时,小的测角误差就会引起较大的定位误差;因此在混合滤波中,应减小对低精度测角信息的信任程度。

对比UKF与EKF过程,EKF需要计算观测向量对状态向量的偏微分雅可比矩阵,当应用于测量模型建立在测站地平坐标系下的非完备观测数据混用算法时,其计算过程较复杂且容易出错;另外,EKF的线性化过程给估计带来了一定误差,使得该方法的滤波发散可能性增大。因此非完备数据混合方法的计算过程更多地使用UKF滤波。

3 数值仿真及分析

3.1 仿真条件

在所有可用测站共视弧段内,仿真时间段相同的情况下,使用几类不同的非完备外测数据来验证变维融合算法的可行性。计算时,采用的滤波状态向量包括J2000惯性系下的位置、速度、加速度、单位质量的质量变化率,测量方程为J2000惯性系下状态量到测站地平系下的外测观测量的转换。给定2013年3月8日8时的1组轨道根数如表1所示。

表1 轨道根数Table 1 Orbital element

3.2 算例1

外推计算单站测距、测角(含方位角及仰角)、测速数据并分别添加100 m,0.02°,0.1 m/s的随机噪声,使用UKF算法对测距、测角、测速齐备的数据及各类测元均不同帧的非完备数据进行混合计算。由半长轴与轨道外推半长轴之差得到轨道半长轴偏差σA,结果如图1所示。可以看出,两种方法计算的半长轴偏差曲线基本吻合。

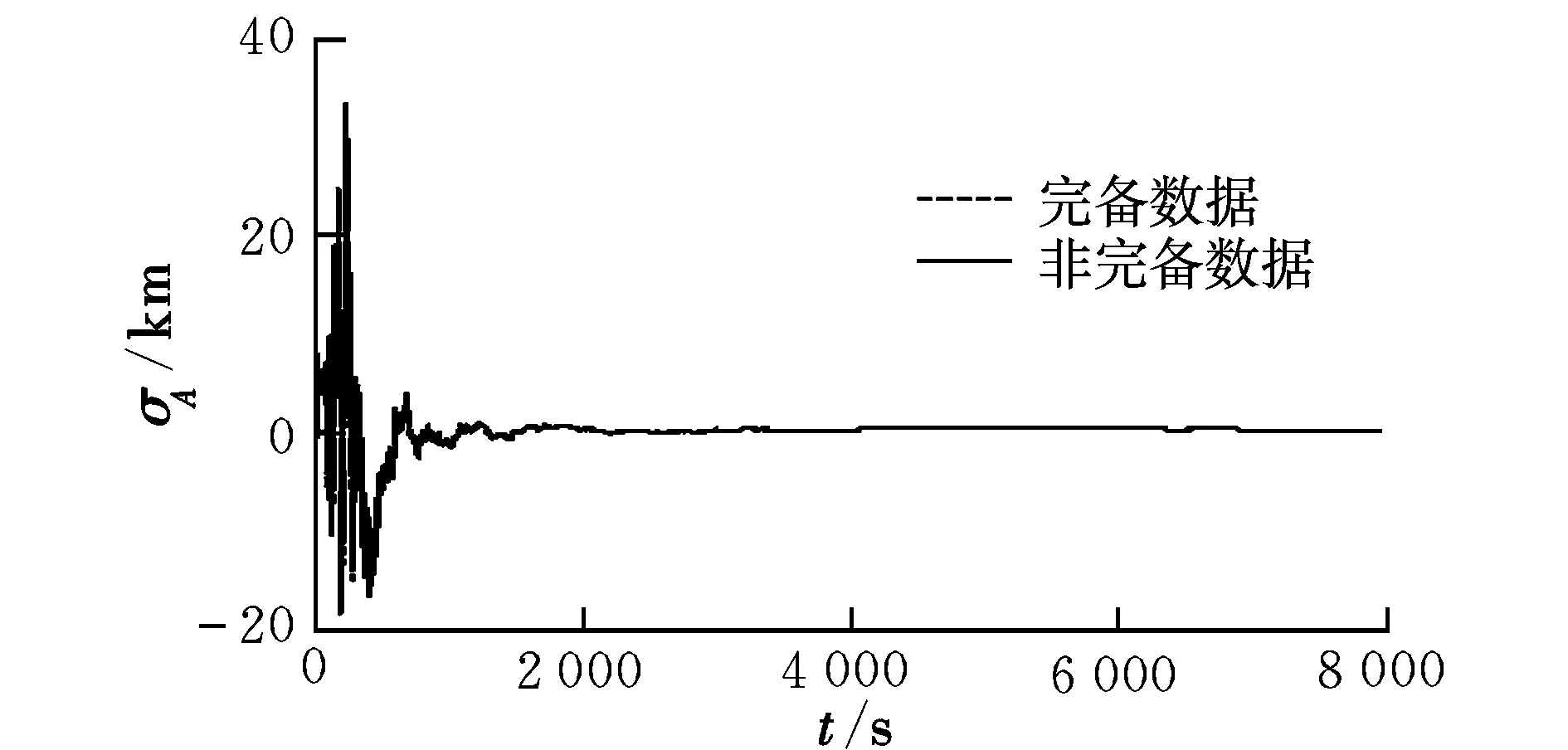
图1 算例1轨道半长轴偏差Fig.1 Orbit semimajor axis deviation for example 1

3.3 算例2

分别使用单站测距及三站测距数据(三站均加上随机噪声)进行滤波,滤波时相关计算参数(滤波系数)保持不变,计算得轨道半长轴偏差如图2所示。

从图2中可看出,使用单站测距数据比三站测距数据滤波时的收敛速度明显降低(仿真数据未考虑各站系统差),而且单站滤波在6 600 s左右出现异常,即只用单站测距是不稳定的(此结论只针对此仿真样本数据及滤波算法设定的系数)。

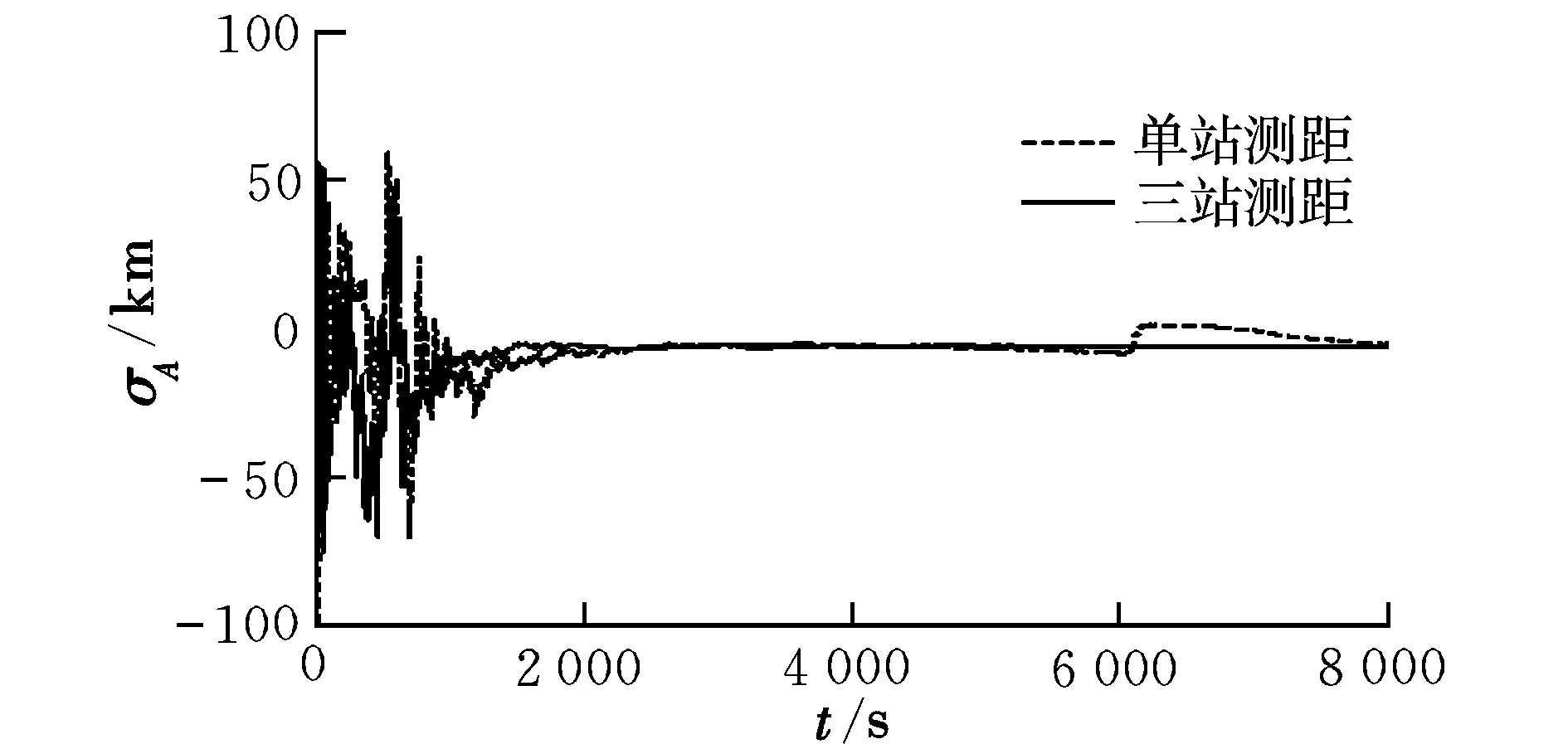
图2 算例2轨道半长轴偏差Fig.2 Orbit semimajor axis deviation for example 2

3.4 算例3

考虑到卫星高度较高时,小测角误差将引起较大的定位误差,当有较高精度的测角设备(如光学设备测角精度高于雷达)时,在混合滤波中可直接将雷达测角标志置为不可用。先仿真一个站的测距、测角数据,分别给定100 m及0.02°的随机差进行滤波计算;再仿真一个站的测角数据,给定5″的随机差,然后将第一站测角屏蔽,使用两站非完备数据进行滤波计算。两种方法得到的半长轴偏差如图3所示。可以看出,因为第二站的测角比第一站测角精度高,滤波收敛速度明显加快。

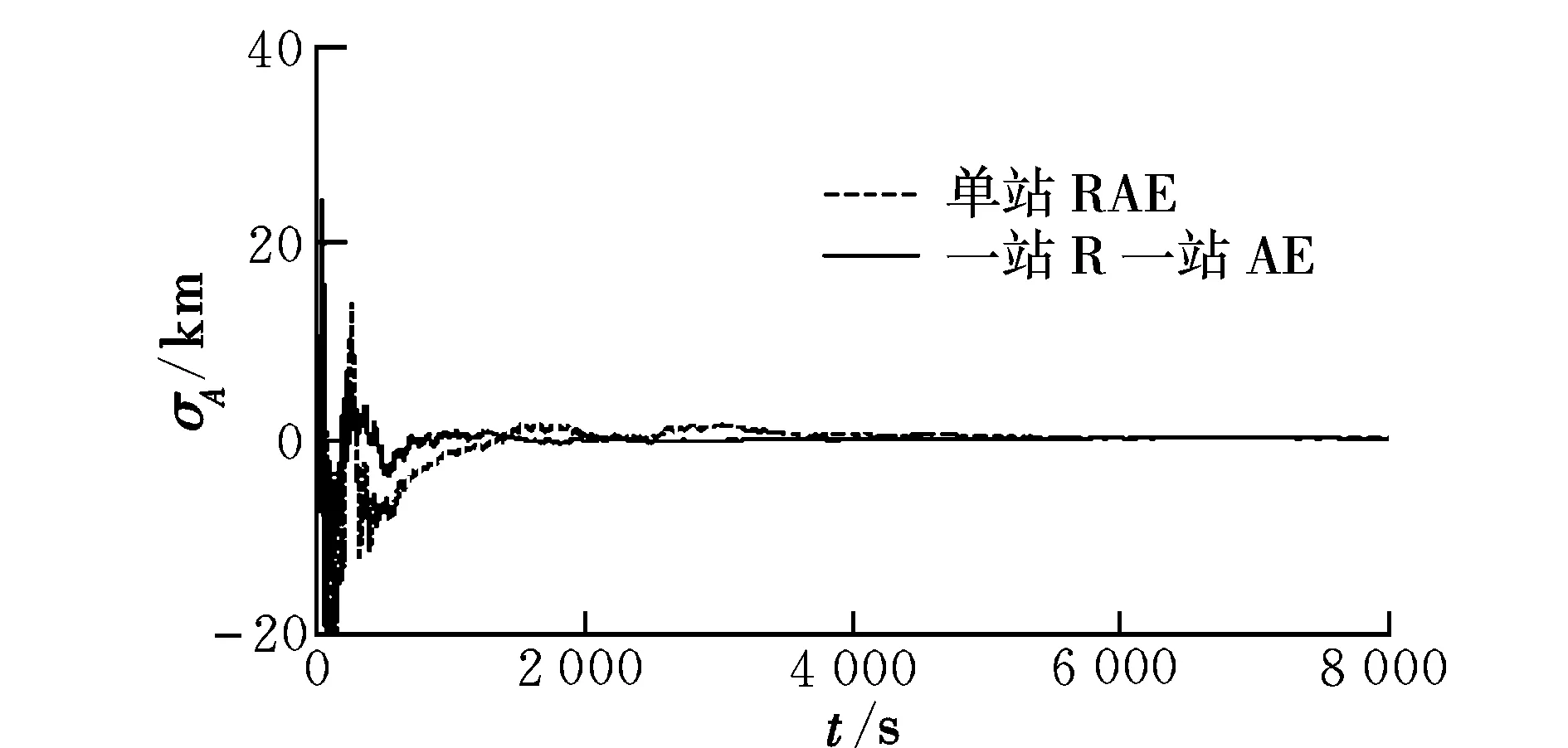
图3 算例3轨道半长轴偏差Fig.3 Orbit semimajor axis deviation for example 3

3.5 算例4

使用算例1的仿真数据,改用EKF滤波算法,使用单站非完备数据计算得半长轴偏差如图4所示。可见,EKF算法中基于变维运算进行非完备数据混用也可以得到较好的结果。

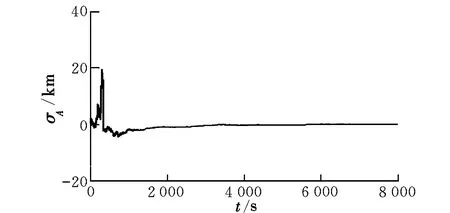
图4 算例4轨道半长轴偏差Fig.4 Orbit semimajor axis deviation for example 4

4 结束语

通过在滤波计算中设置测元有效标志,并使用变维矩阵运算的途径来实现非完备观测数据混用的方法是可行的,其计算结果可以达到与完备数据同样的精度。非完备观测数据混用滤波的收敛性及精度与非完备测元的种类、多站的观测几何等相关。非完备数据混用过程中,可以通过对某些精度差的测元设置“不可用”标志的方法减少对计算精度的影响。此种基于非完备观测信息的实时定轨方法对UKF,EKF等滤波算法都是适用的。

在实时滤波定轨中直接使用非完备数据的方法有助于减小外测数据预处理的复杂度,具有一定的实用价值。后续将重点在混用过程中的机动过程检测、测元的动态取舍等方面进行研究。

参考文献：

[1] 慈颖,郭军海.基于UKF的测速定轨实时算法[J].飞行器测控学报,2007,26(6):59-62.

[2] 吴盘龙,蔡亚东,王宝宝.仅测角卫星跟踪的扩展卡尔曼粒子滤波算法[J].红外与激光工程,2011,40(10):2008-2012.

[3] 曹志高,高源,程洪玮.单星只测角对低轨卫星的EKF跟踪分析[J].飞行器测控学报,2007,26(6):70-75.

[4] 孟繁智,吴向宇,欧钢.联合星间测距和测速的导航星座自主定轨研究[J].飞行器测控学报,2010,29(4):89-94.

[5] 祝转民,杨宜康,黄永宣,等.定位与测速数据融合估计弹道稳定性与精度分析[J].中国空间科学技术,2003,(4):30-34.

[6] Wan E A,Van der Merve R.The unscented Kalman filter for nonlinear estimation [C]//Proceedings of Symposium 2000 on Adaptive Systems for Signal Processing,Communication and Control(AS-SPCC).Canada:IEEE,2000:153-158.

[7] 彭丁聪.卡尔曼滤波的基本原理及应用[J].软件导刊,2009,8(11):32-34.

[8] Li X R,Jilkov V P.Survey of maneuvering target tracking.ParkⅠ.Dynamic models[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1333-1364.

[9] 柳海峰,姚郁.Kalman滤波抗野值方法研究[J].计算机自动测量与控制,2001,9(6):60-61.

[10] 祝转民,秋宏兴,李济生,等.动态测量数据野值的辨识与剔除[J].系统工程与电子技术,2004,26(2):147-149.

[11] 卢迪,姚郁,贺风华.一种抗野值的Kalman滤波器[J].系统仿真学报,2004,16(5):1027-1029.