基于稳定裕度的控制系统双回路增益优化方法

赵金龙, 周军, 郭建国, 呼卫军

(西北工业大学 精确制导与控制研究所, 陕西 西安 710072)

0 引言

对于远程火箭或弹道导弹而言,其主动段控制系统设计通常是在标准弹道上选取若干特征点,确定控制系统构型并对特征点逐个进行增益优化,进而通过增益调度实现全包线飞行控制律。对于控制系统增益优化问题,传统试凑的方法效率低且优化效果不明显,难以同时满足时域指标和频域稳定裕度要求。因此,对控制系统增益自动优化问题的研究,日渐受到诸多学者的关注。

控制系统增益优化实际上是一个多约束非线性最优化问题,目前已将多种现代优化算法研究应用于控制系统增益设计,如遗传算法[1]、禁忌搜索算法[2]、蚁群算法[3]、神经网络[4]和序列二次规划[5]等。神经网络算法学习过程收敛较慢,还可能出现误差在一定时间范围内并不随学习次数增加而减小的“假饱和”现象;蚁群和微粒群等算法同样缺乏充分的理论依据,算法参数设定过度依赖于经验,优化结果带有一定的随机性。文献[6-7]直接基于时域响应性能指标设计增益最优化问题的目标函数,该方法在特征点上的动态响应性能良好,但未考虑系统相对稳定性,难以确保控制系统鲁棒性和稳定性。

本文基于频域稳定裕度构造目标函数,采用广义拉格朗日乘子法处理不等式约束项,将问题转化为无约束最优化问题,构造了一种双回路求解算法获得控制系统增益最优解。优化结果使得控制系统不仅满足时域响应性能指标,而且具备较大的幅值裕度和相角裕度,系统鲁棒性和稳定性均有较大提高。

1 系统控制律设计

远程火箭主要通过摆动发动机控制箭体的推力方向实现弹道修正,使其沿着预先选定的标准弹道飞行。而箭体的推力方向主要由刚性箭体的姿态角决定,因此,姿态控制系统的任务就是根据导航制导信号控制箭体姿态角。

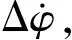
以俯仰通道为例,姿态角偏差和姿态角速度偏差反馈控制的姿态控制系统框图如图1所示。

俯仰控制律数学表达式为:

(1)

式中,δφ为摆动发动机俯仰方向偏角;a为增益环节1;b为增益环节2。

由式(1)可见,远程火箭控制系统设计最终归结为调节增益参数a和b,使得被控对象在选定的特征点处快速平稳跟踪指令信号,并保持足够的频域稳定裕度。因此,可通过构造目标函数,并设定增益参数的初值和参数空间,将上述问题转化为不等式约束的非线性最优化问题。

2 双回路增益优化方法

2.1 目标函数构造

为了使系统具有最大的相对稳定性,提高控制系统在特征点及其邻域内的鲁棒性和稳定性,本文基于频域稳定裕度指标设计目标函数。

当考虑液体晃动或弹性振动时,远程火箭或弹道导弹的控制系统是一个多模态宽频域综合设计问题,存在多个相角裕度和幅值裕度指标。

相角裕度指标可表示为:

γ=[γ1,γ2,…,γm] (2)

式中,γi表示第i个截止频率的相角裕度。

幅值裕度指标可表示为:

H=[h1,h2,…,hn] (3)

式中,hj表示第j个相角交界频率的幅值裕度。

用X=[x1,x2,…,xl]表示l个增益组成的优化变量,则通过频域稳定裕度指标加权法构造目标函数如下:

f(X)=AγT+BHT(4)

式中,A=[a1,a2, …,am]为相角裕度权系数;B=[b1,b2, …,bn]为幅值裕度权系数。

设增益寻优的参数空间为[d,u],则约束条件可表示为:

X∈[d,u] (5)

式中,d=[d1,d2,…,dl]为参数空间下边界;u=[u1,u2,…,ul]为参数空间上边界。

由式(5)可知,目标向量X约束条件为di≤xi≤ui(i=1,2,…,l),因此,控制器增益优化问题可转化为不等式约束的最优化问题:

(6)

式中,g2i-1(X),g2i(X)为不等式约束条件;i=1,2,…,l。

2.2 广义拉格朗日乘子法

针对式(6)的约束最优化问题,为了降低算法复杂度、减小计算量,首先将其转化为无约束最优化问题。通常采用的罚函数法能够利用求解无约束极值问题的算法来求解约束极值问题,但由于目标函数f(X)在约束极大点处的梯度一般是非零的,使得罚函数法不能通过有限次无约束极大化而得到约束极大点[8]。

本文采用广义拉格朗日乘子法[9],将罚函数和拉格朗日函数结合起来,构造出更合适的新目标函数,使得在罚因子M适当大的情况下就能逐步达到原约束问题的最优解。首先,通过添加松弛变量Z=[z1,z2,…,z2l]T将式(6)转化为等式约束最优化问题:

(7)

构造惩罚函数进一步将上述问题转化为无约束最优化问题:

(8)

式中,第二项用于解决传统惩罚函数中目标函数之间的不匹配性,第三项用于保证优化向量超出可行域时惩罚项取值为负。

根据极大值原理求解式(8)可得:

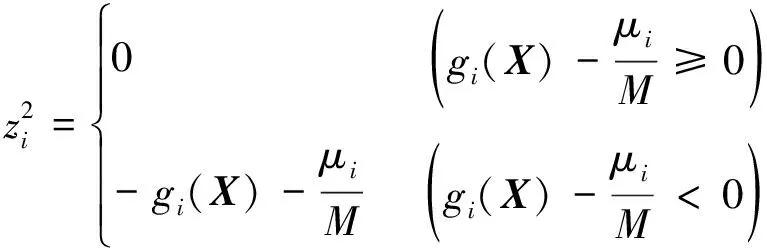
将式(9)代入式(8)可得最终形式的无约束最优化问题:

maxF(X)=

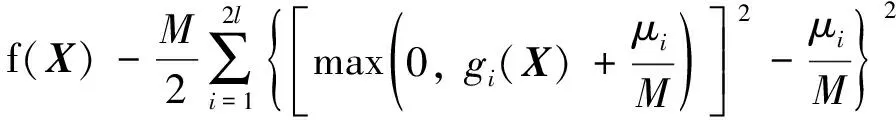
式中,M为罚因子;μi(i=1,2,…,2l)为拉格朗日乘子。

只要选取适当大的罚因子M>0,就可以通过一次无约束极大化得到不等式约束极大问题的解。但M和μi的取值无根据,因此,采用逐步迭代的方式,逐步增大M并调整μi后求解无约束极大问题,直至精度指标满足要求。广义拉格朗日乘子法计算流程如图2所示,设最大迭代次数kmax=50,残差最大值ε=1.0e-3,M和μi的迭代规则如下:

(11)

式中,k为迭代次数,α为扩大因子,取值为2。

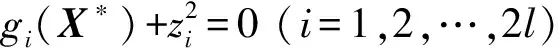
(12)

将式(9)代入式(12)可得:

(13)

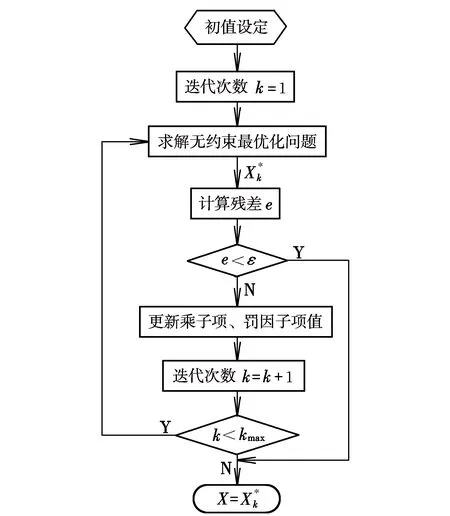
图2 拉格朗日乘子法流程图Fig.2 Flow diagram of the Lagrange multiplier method

由图2可见,广义拉格朗日乘子法求解无约束最优化问题分为内回路和外回路:外回路通过罚因子M和乘子μi逐步迭代来调整目标函数,内回路则不断求解无约束最优化问题,直至优化变量满足精度要求或达到最大迭代次数。

2.3 单纯形搜索算法

内回路中对于无约束最优化问题的求解采用单纯形算法[8]。单纯形算法是一种基于图形变换的优化算法,其基本思想是:对于n维优化向量,由n+1个顶点构成多面体单纯形,根据各点上的目标函数值大小进行优胜劣汰,同时按照判定规则确定新的顶点构成新的单纯形,不断变换直至获得满足精度要求的优化向量值。

单纯形算法的基本变换规则包括反射、延伸、压缩、收缩等,以二维搜索向量X=[x1,x2]为例,单纯形为Ox1x2平面上的三角形,其顶点分别为Xh,Xg和Xl,对应的目标函数值依次分别为fh,fg和fl,且满足fh>fg>fl。单纯形算法求解控制器增益无约束最优化问题的流程参见文献[8]。

(1)计算最坏点Xl的反射点

(14)

式中,反射系数取ρ=1。

(15)

式中,延伸系数取β=2。

外压缩:

(16)

内压缩:

(17)

式中,压缩系数γ∈(0,1),取γ=0.5。

(4)收缩,即减小棱长:

(18)

式中,收缩系数σ=0.5。

本文设定单纯形优化搜索算法的终止条件:

|fh-fl|<ε|fl| (19)

式中,ε为表征目标函数精度的值,取ε=1.0e-4。

3 仿真算例与结果分析

以某型远程火箭主动段控制系统的俯仰通道为例,根据俯仰程序角曲线选择若干个特征点,通过数值方法在特征点上计算Jacobian矩阵实现箭体模型小扰动线性化,获得纵向传递函数模型。

根据式(1)控制律,设计增益优化变量为:

X=[a,b] (20)

式(6)中目标函数的权系数设为:

A=[1,…,1],B=[1,…,1] (21)

采用VC++对本文的增益优化方法编程实现,三种不同的优化变量参数及优化结果如表1所示。

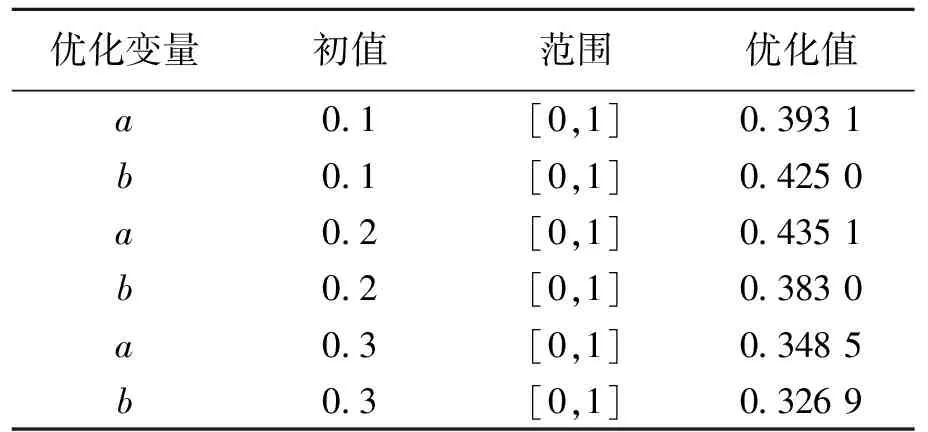
表1 仿真参数Table 1 Parameters of the simulation

图3所示为优化变量参数空间范围内,约束最优化问题式(6)的目标函数值随迭代次数的变化曲线。可见,对于不同的优化变量初值,目标函数均可快速收敛至极大值。

三组不同仿真参数在特征点上时域阶跃响应曲线如图4所示,频域Bode图如图5所示。优化变量初值对阶跃响应有影响,但均可保证控制稳定性,频域稳定裕度指标如表2所示。

由图3～图5可知,广义拉格朗日乘子结合单纯形法的设计思想可有效应用于控制系统增益优化,收敛速度较快。增益优化结果不仅能保证良好的时域响应性能,而且具备较高的稳定裕度。

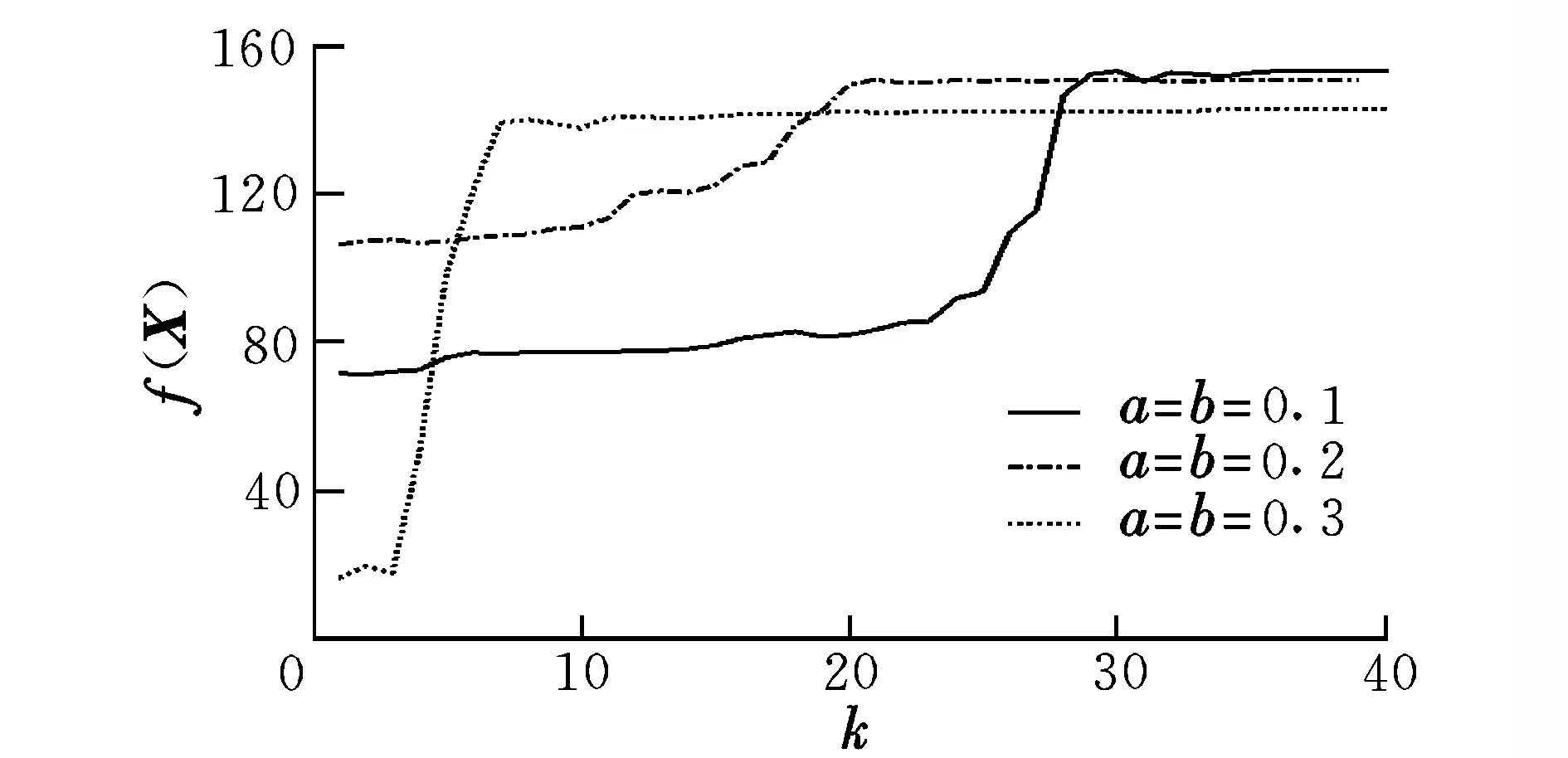
图3 目标函数变化曲线Fig.3 Outputs of the objective function

图4 俯仰通道阶跃响应曲线Fig.4 Step responses of the pitch channel

图5 俯仰通道频域bode图Fig.5 Bode diagram of the pitch channel

优化变量初值幅值裕度/dB相角裕度/(°) a,b0.125.283.20.224.382.40.325.675.5

4 结束语

本文结合某型远程火箭俯仰通道控制系统,基于频域稳定裕度指标构造目标函数,并提出了一种双回路增益优化方法。仿真结果表明,本文所设计的控制系统增益优化方法能够满足时域和频域指标要求,有效改善了控制系统的鲁棒性和稳定性,可应用于PID等多种控制系统构型,具有一定的工程应用价值。

参考文献：

[1] Herrero J M,Blasco X,Martinez M,et al.Optimal PID tuning with genetic algorithms for non-linear process models[C]//IFAC 15th Triennial World Congress.Barcelona,Spain,2002:1009-1014.

[2] Aytekin Bagis.Tabu search algorithm based PID controller tuning for desired system specifications[J].Journal of the Franklin Institute,2011,348(10):2795-2812.

[3] 尹宏鹏,柴毅.基于蚁群算法的PID控制参数优化[J].计算机工程与应用,2007,43(17):4-7.

[4] 赵卫华.基于神经网络参数优化的PID控制研究[D].太原:中北大学,2008.

[5] 陈怀民,徐奎,王鹏,等.基于无尾飞机横侧向控制律参数优化设计的一种方法[J].西北工业大学学报,2007,25(4):585-589.

[6] Awouda A E A,Bin Mamat R.Refine PID tuning rule using ITAE criteria[C]//Computer and Automation Engineering(ICCAE),2010 the 2nd International Conference.Singapore,2010:171-176.

[7] 张民,陈欣,陆宇平.基于改进PSO算法的导弹控制参数优化[J].南京航空航天大学学报,2009,41(4):445-449.

[8] 张光澄.非线性最优化计算方法[M].北京:高等教育出版社,2005:99-107.

[9] 粟塔山.最优化计算原理与算法程序设计[M].长沙:国防科技大学出版社,2002:151-164.