基于自抗扰控制算法的两轮自平衡车分析
胡 建,颜钢锋
(浙江大学 电气工程学院,浙江 杭州 310027)
0 引 言
两轮自平衡车属于轮式机器人的范畴,体积小、结构简单、运动灵活,特别适于在狭小和危险的空间内工作;同时由于它具有不稳定的动态特性,是一个典型的倒立摆运动模型[1-3],两轮自平衡车成为验证各种控制算法的理想平台,具有重要的理论意义。它的工作原理是:系统利用陀螺仪和加速度传感器,检测出车身的俯仰状态以及状态变化率,通过中央处理器计算并发出命令,驱动电机加速向前或向后等动作来保持车体的平衡。驾驶者只需通过前倾或后仰来控制车子的速度,通过转向把手来控制左右的转向。它属于典型的非线性、时变、欠驱动、非完整约束系统,解决它的控制问题是其研究的关键。
本研究首先运用牛顿动力学分析的方法,对两轮自平衡车分别进行运动学和动力学的分析,从而得到系统的数学模型,为控制器设计实现提供可靠的理论依据。笔者根据著名的解耦定理[4],将系统解耦成平衡与转向两个子系统分别来控制。针对具有强非线性的前进子系统,论证基于近似线性化、精确线性化及自抗扰控制控制策略的应用可行性。利用Matlab中Simulink模型对自抗扰算法进行仿真,并通过搭建的两轮自平衡车控制系统实验平台进行实验,获得期望的平衡效果,以验证该算法的正确性与有效性。
1 两轮自平衡车的动力学模型
要定量、准确地分析设计一个控制系统,认识研究对象,提高控制能力,一定要建立控制对象的数学模型。精确地确立两轮自平衡车的数学模型,是解决其控制问题的关键之一。
为了实现两轮自平衡车的运动状态控制,需要建立其运动学模型。本研究以右轮和车体为研究对象,进行受力分析,受力分析图如图1、图2所示。
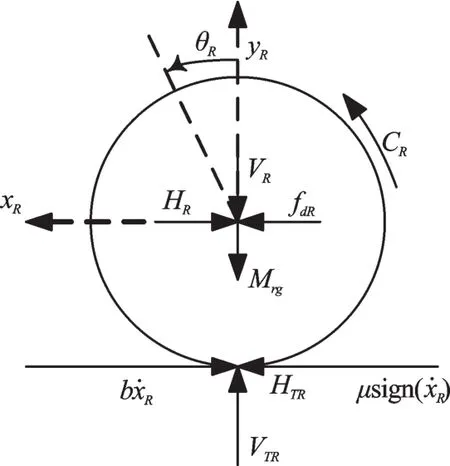
图1 对右轮进行受力分析
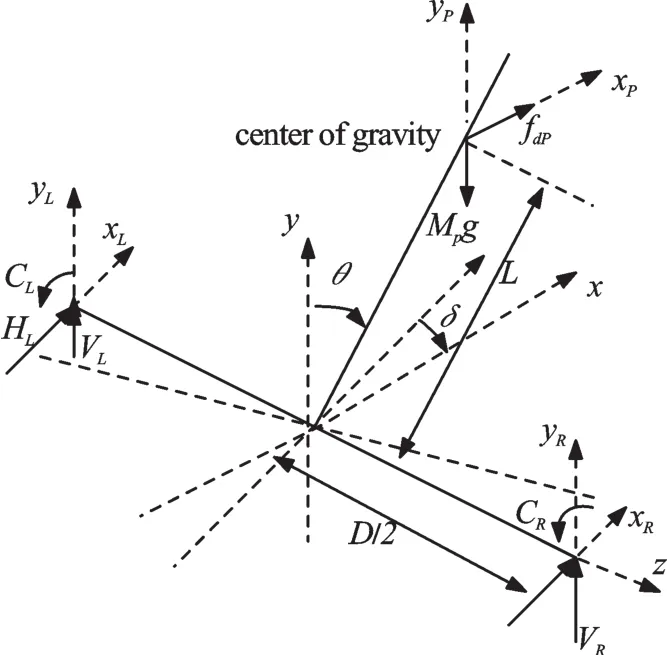
图2 车体的受力分析
首先,将推导公式中要用到的符号作如下说明:
VR[m/s],VL[m/s]—左右电机的速度;
MR[kg],ML[kg]—左右电机的质量;
JR[kg·m2],JL[kg·m2]—左右电机的相对于z轴转动惯量;
CR[N·m],CL[N·m]—左右电机的输出转矩;
θ[rad]—车体向前的倾角;
ω[rad/s]—车体向前的角速度;
Jθ[kg·m2]—车体相对于z轴的转动惯量;
δ[rad]—转把的转向角;
δ·[rad/s]—转把的转向角速度;
Jδ[kg·m2]—车体相对于y轴的转动惯量;
MP[kg]—车体的质量(包括驾驶人的质量);
V[m/s]—两轮自平衡车向前行驶的速度;
R[m]—电机的半径;
D[m]—两电机车轮中心的横向距离;
L[m]—车体的重心到Z轴的距离;
b—库仑摩擦系数;
μ—粘滞摩擦系数。
由力学知识可知,库仑摩擦力fc=μsign(V),粘滞摩擦力fb=bV。
(1)对于右轮受力分析如图1所示,运用牛顿定律可知:

同理,左轮的力学方程为:

(2)对于车体的受力分析如图2所示,有如下的力学方程:
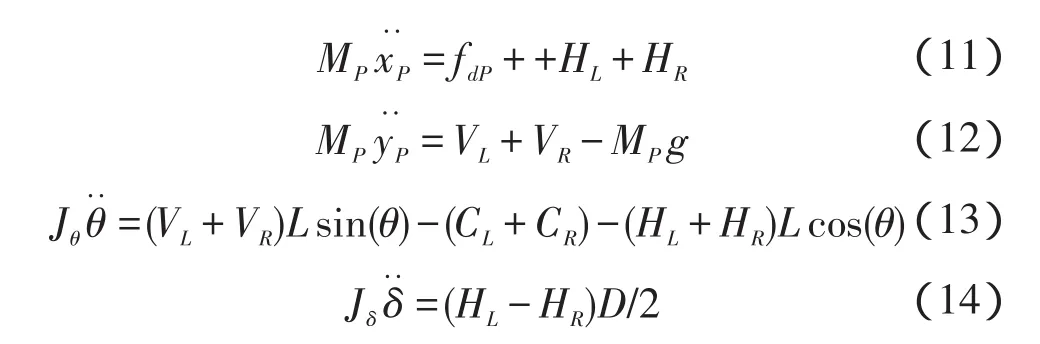
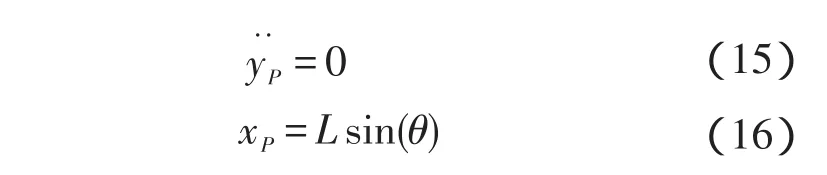
(3)解上面的方程组,求出系统的数学模型。
由相关知识可知,JL=JR=J,x=(xR+xL)/2=R(θR+θL)/2,MR=ML=M,那么,可以先求出:
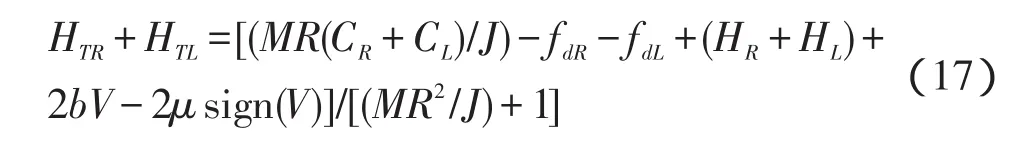
由式(6,7,9),可得:
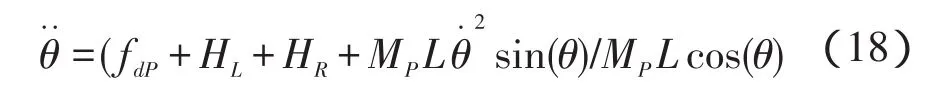
由式(13,18),得:
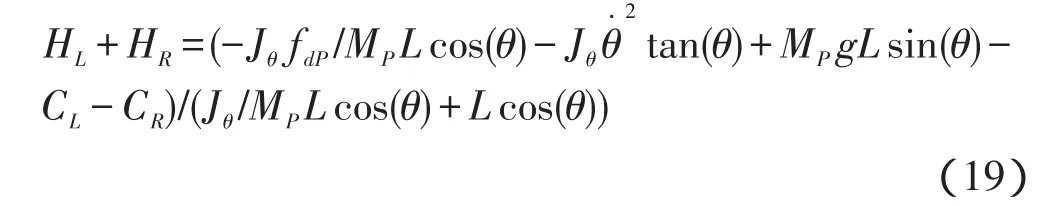
由式(1~10),得:
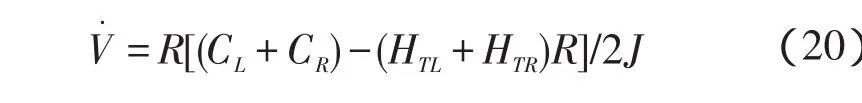
将式(18,19)代入式(20),则有:
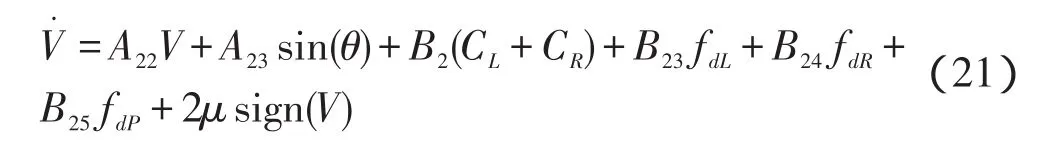
其中:
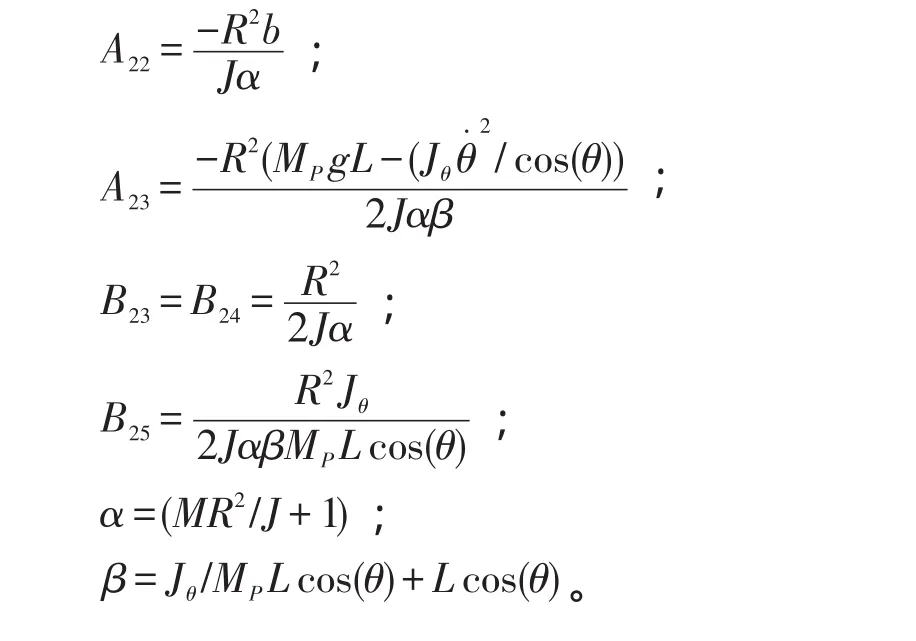
由物理学知识知,ω=θ·,则有:

其中:
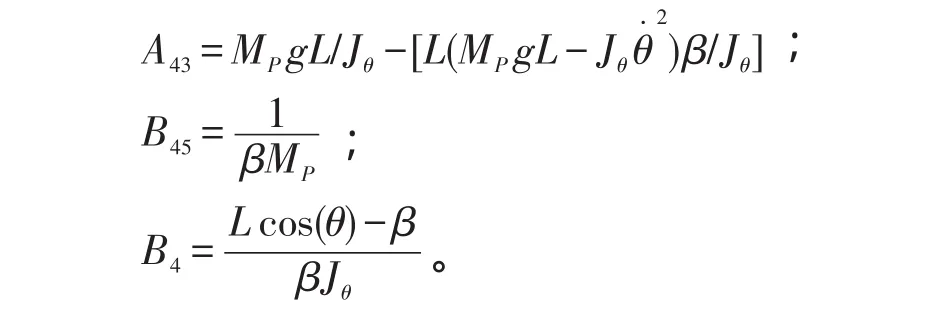
对于转向,有δ·=(VL-VR)/D,结合式(1,6),可化简为:
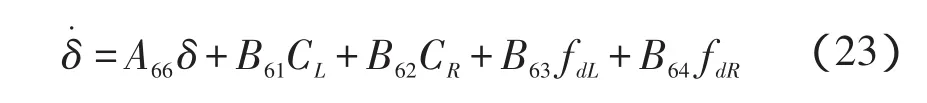
其中:
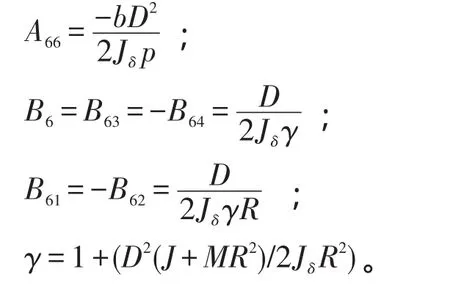
从上述分析可以看出两轮自平衡车的模型是一个非线性模型,如果采用经典的控制理论方法则需要将θ限制在 0度附近很小的范围内(即:sin(θ)≈θ,cos(θ)≈1)作近似处理,得到线性化的模型。而本研究采取的方法,则是根据现代控制理论,选择一组状态变量来描述上述系统的动态特征,就可以确定系统的未来状态和输出。在两轮自平衡车所建立的模型基础上,笔者所选的状态变量为则该系统的状态空间[5]非线性方程为:
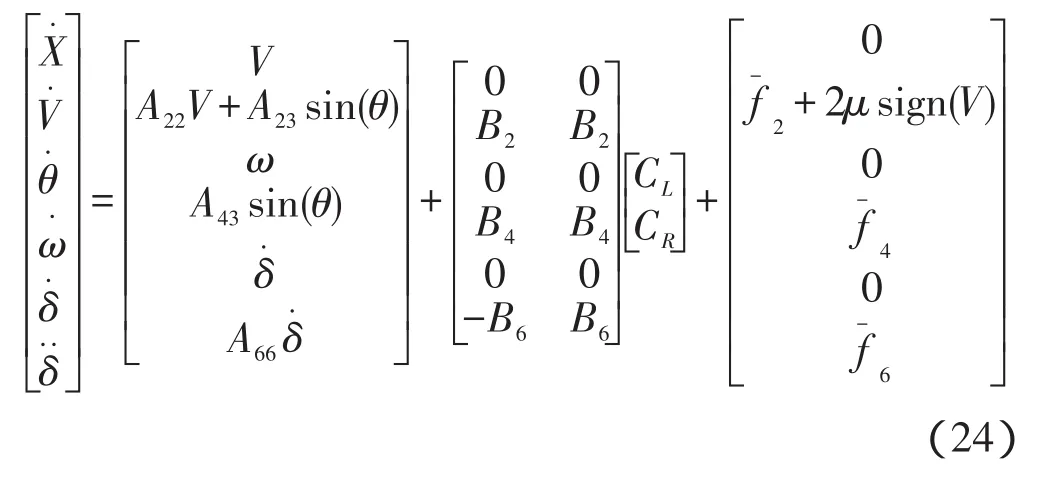
其中:
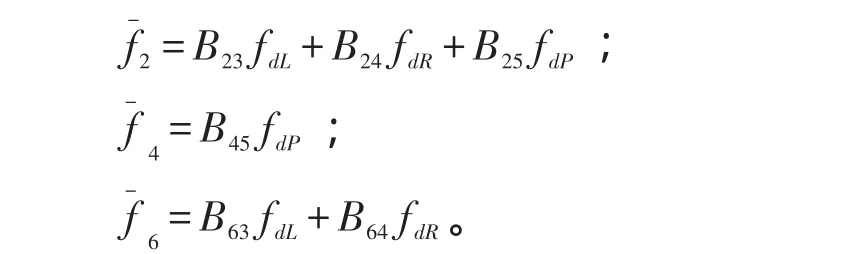
本研究利用状态空间模型来分析非线性系统,利用Matlab强大的矩阵运算能力来进行系统仿真和分析系统的动态和静态性能,也为下面控制系统的解耦成两个子系统奠定模型基础。
2 控制策略
在这里忽略电机的模型,因为电机的时间常数远比系统的时间常数小,这个动力学模型可被解耦成两个子系统来控制[6],即:
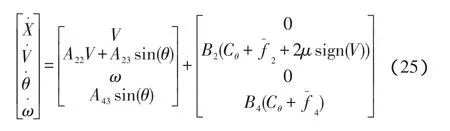

式中:Cθ—控制平衡所需要的电机输出转矩,Cδ—转向所需的电机输出转矩。
首先,忽略fdL,fdR,fdP,因为它们是扰动力,不能用来控制系统,而2μsign(V)值很小,先作忽略来处理。从解耦出来的平衡状态的数学模型可知,当θ和V为常值时,则它们各自的微分量ω=0,V·=0,那么Cθ=-A43θ/B4,两轮自平衡车也将保持一个恒定的速度V=(A43B2-B4A23)θ/A22B4。因此,当驾驶者向前倾斜到一个恒定的角度θ时,为了不使其倒下来,两轮自平衡车必须到达一个恒定的速度V。
从以上的模型中可以看出,由于驾驶者和其他因素对平衡车系统的影响不同,导致系统的参数大小变化,根据这些情况实时地输出系统所需的电机转矩,就需要考虑到自适应算法[7],它介绍了鲁棒控制自适应的控制方法,让系统根据实际要求输出所需的转矩。针对控制系统参数的不确定和扰动作用的不同,下面,本研究介绍引进了一种控制算法,它是由我国著名的韩京清研究员建立并推广使用的自抗扰控制,把系统中未建模部分和其他因素导致系统变化的部分当成总扰动来补偿控制量。
3 自抗扰控制技术
自抗扰控制技术[8-12]是从经典的PID控制理论演变而来的,采取的是PID误差反馈控制的核心理念。该控制技术由跟踪微分器、扩张状态观测器和非线性状态误差反馈律3部分组成。
各部分的功能分别如下:
(1)跟踪微分器的功能是为系统输入安排过渡过程,得到光滑的输入信号以及输入信号的微分信号。
(2)扩张状态观测器(ESO)的功能是实时跟踪系统状态,不仅能得到系统的状态信息,还能获得对象模型中内扰和外扰的实时作用量。通过将这个实时作用量补偿到控制器中去,可以使原来的非线性系统变成线性的积分器串联型控制系统。这个动态估计补偿总和扰动的技术是整个自抗扰控制技术中最关键、最核心的技术。
(3)非线性状态误差反馈律的功能是把跟踪微分器产生的跟踪信号和微分信号与扩张状态观测器得到的系统的状态估计通过非线性函数进行适当组合,作为被控对象的控制量。
自抗扰控制技术中,非线性函数形式有多种,典型的二阶自抗扰控制器的算法如图3所示。

图3ADRC结构框图
3.1 安排过渡过程
为了得到微分信号,可以用下面最快地跟踪给定信号的办法来提取微分信号的非线性最速跟踪微分器:
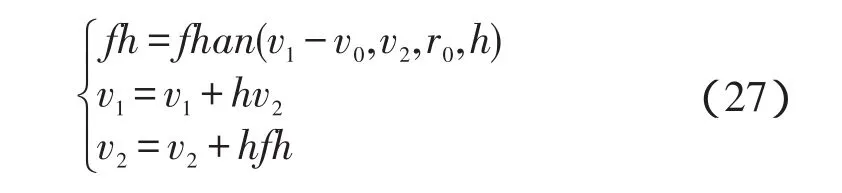
式中:v0—系统的参考输入信号;v1—安排过渡过程,无超调;v2—其微分信号。
其原则为:选加速度形状,先正后负,正部分的面积与负部分的面积相等;积分两次,得单调上升、无条件超调的过渡过程。
fhan(x1,x2,r,h)的定义如下:
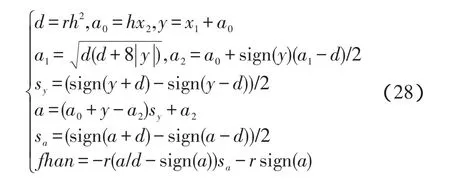
3.2 估计状态和总振动(ESO)
扩张状态观测器是一个动态过程,它只用了原对象的输入-输出信号,没有用到描述对象传递关系的函数的任何信息,它的状态方程用如下表达式表示:
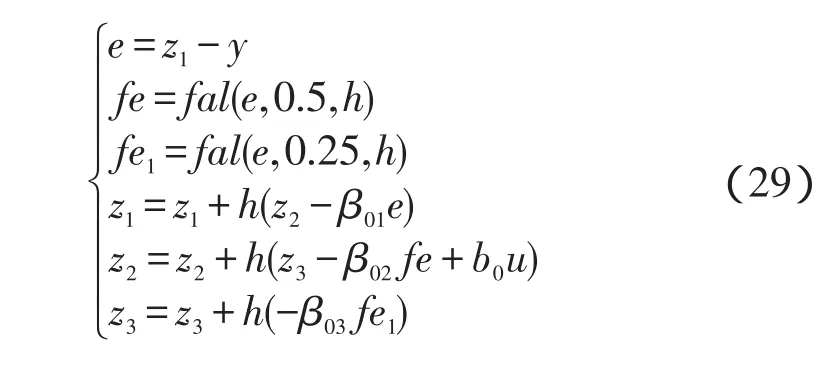
式中:z1,z2—实时估计对象的状态;z3—扩张的状态即为估计系统的总扰动。
3.3 非线性误差反馈
对于误差反馈,可以有很多种反馈形式,有线性的也有非线性的组合。考虑到两轮车系统为一个非线性系统,采用下面的最速控制综合函数形式来反馈:
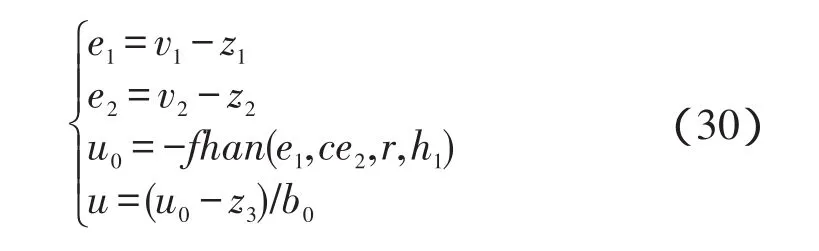
上式中,非线性函数fal(e,α,d)的定义如下所示:
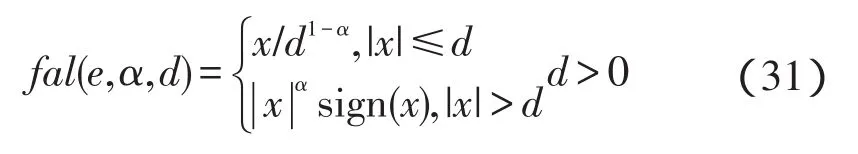
这里不再需要“误差积分”反馈。“自抗扰”意义在于“补偿”项-z3(k)/b,系统的“未建模动态”和“未知外扰”作用一并给予估计和补偿。
在控制器中,β01,β02,β03,c,r,h1,b0是控制器的参数,r0是根据过渡过程快慢的需要和系统所能承受的能力决定的,只影响系统的跟踪精度和过渡过程时间,对系统的输出没有影响,因此调整好之后就可以固定下来;参数β01,β02,β03是由系统所用采样步长来决定的。所以,自抗扰控制系统中真正需要调整的参数为控制量增益r,阻尼系数c,精度因子h1和b0补偿因子4个。在一般情况下,控制量增益r是大到一定程度就可以,再大也几乎没有影响。
4 仿真与实验
由于两轮自平衡车的参考位置为θ=0,则可以不安排合适的过渡过程,对于该系统来说,利用自抗扰控制的扩张状态观测器来估算系统的总扰动,作为控制对象输入的补偿即可:
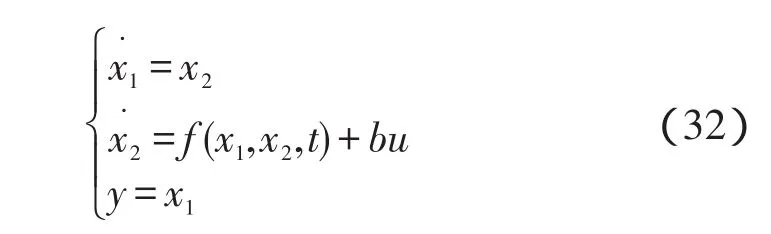
f(x1,x2,t)未知,包含建模中不能确定的所有量。
假定e(k)=z1(k)-y(k),则离散化的ESO为:
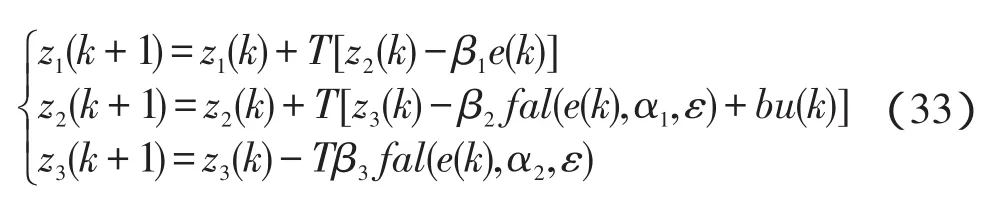
系统的总输入量为:

对于非线性误差反馈,其实它的反馈形式有线性和非线性反馈等多种形式,而在两轮自平衡车的系统中,状态量x1和x2,也即θ和ω可以通过加速度与陀螺仪传感器分别测量,通过kalman滤波算法[13-15]可以得到精确的状态信息,反馈形式可取为如下的线性形式,即:
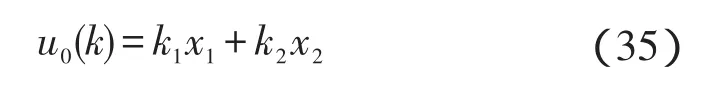
为了从理论上验证算法的可行性,本研究首先进行仿真论证。仿真给定初始的角度扰动为5°,利用Matlab中的Simulink模型来搭建系统模型,得到的仿真波形曲线如图4所示。下面为实验测得的两轮车参数:
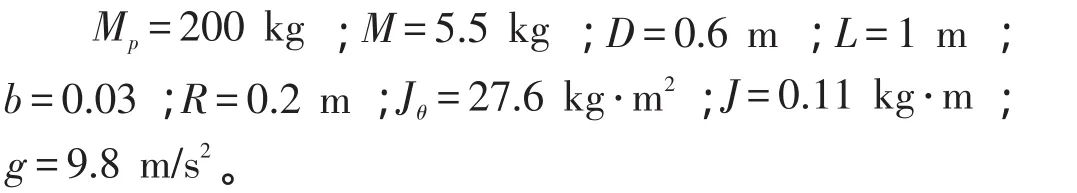
图4中,曲线线型的含义如下:虚线表示车的速度V,实线表示倾角θ,点划线表示角速度ω。从图4中可以看出,自抗扰控制能抑制初始的扰动,补偿输出控制量让车的状态回到θ=0的平衡态,且获得一定的速度向前行驶,与理论分析一致,说明该方法的正确性。
为了做到理论与实践相结合,以便更好地验证算法的正确性,本研究利用ARM公司的Cortex-M3内核的嵌入式微处理器作为主处理芯片来实现自抗扰控制算法,所做的控制器硬件图如图5所示。

图4 仿真波形曲线

图5 实验控制器

图6 不同重量的驾驶者斜坡行驶
为了更好地验证算法,笔者在实验室做的自平衡车体上进行实物实验,用不同重量的人,在斜坡上驾驶着小车,取得了满意的效果,所得到的实验效果如图6所示。不同质量的人在一个大于15°的斜坡上驾驶小车,小车均可以平稳地运行,不会出现不稳定的情况,不会因为人或者运行在地况不好的路段而出现不稳定、不平衡的情况,则说明自抗扰算法能较好地用于自适应地估算系统的扰动并进行控制补偿。
5 结束语
本研究从两轮自平衡车的物理模型着手分析,运用牛顿力学分析出其对应的数学模型,并结合自抗扰控制技术对系统进行了仿真分析,从理论上验证了算法的可靠性。自抗扰控制技术的核心是把系统的未建模动态和未知扰动作用都归结为对系统的“总扰动”而进行估计并给予补偿,采用的方法是充分利用特殊的“非线性”效应,将一些摩擦力、不同重量的驾驶人员和未知的扰动统一归为对系统的总扰动来处理,重点利用ESO来估算这个扰动的大小,对系统输入进行补偿。然而对于小车的转向没有作相应的分析,实验中就采取了纯开环的控制,转向的实验效果也较满意。
在今后的研究中,可能需要进一步改进自抗扰参数整定的方法,也将自抗扰控制技术应用到小车的转向控制中,以实现对两轮自平衡车良好的控制,确保系统的稳定可靠。
(References):
[1]CARABEL C J P,GARCIA A A Z.Modeling,control and automatic code generation for a two-wheeled self-balanc⁃ing vehicle using modelica[D].Department of Automatic Control Lund University,2011.
[2]XV Jian-xin,GUO Zhao-qin,LEE T H.Design and imple⁃mentation of a takagi-sugeno-type fuzzy logic controller on a two-wheeled mobile robot[J].Industrial Electronics,IEEE Transaction on,2013,60(12):5717-5728.
[3]ZHANG Da-wei,HAN Qing-long,JIA Xin-chun.Networkbased H∞fuzzy control for a self-balancing two-wheeled inverted pendulum[C]//Industrial Electronics(ISIE),2013 IEEE International Symposium on ,2013:1-6.
[4]GRASSER F,ARRIGO A D,COLOMBI S.JOE:a mobile,inverted pendulum[J].IEEE Transactions on Industrial Electronics,2002,2(1):107-114.
[5]毕沙著.现代控制系统[M].10版.赵千川,冯 梅,译.北京:清华大学出版社,2008.
[6]LIN Shui-chun,TAI Ching-chih,HUANG Hsu-chih.De⁃velopment of self-balancing human transportation vehicle for the teaching of feedback control[J].IEEE Transac⁃tions on Education,2009(2):1-52.
[7]LIN Shui-chun,TSAI Ching-chih,HUANG Hsu-chih.Adaptive robust self-balancing and steering of a twowheeled human transportation vehicle[J].Intell Robot System,2011,27(2):103-123.
[8]韩京清.从PID技术到“自抗扰控制”技术[J].控制工程,2002(5):9-13.
[9]韩京清,王 伟.非线性跟踪—微分器[J].系统科学与数学,1994,14(2):177-183.
[10]韩京清.一类不确定对象的扩张状态观测器[J].控制与决策,1995,10(1):85-88.
[11]韩京清.非线性状态误差反馈控制-NLSEF[J].控制与决策,1995,10(3):22-225.
[12]韩京清.自抗扰控制器及其应用[J].控制与决策,1998,13(1):19-23.
[13]冯智勇,曾 瀚.基于陀螺仪及加速度计信号融合的姿态角度测量[J].西南师范大学学报:自然科学版,2011,8(5):36-40.
[14]陈 晨,赵文宏,徐慧鑫,等.基于卡尔曼滤波的MEMS陀螺仪漂移补偿[J].机电工程,2013,30(3):311-313,321.
[15]KALMAN R E.A new approach to linear filtering and pre⁃diction problems[J].Transaction of the ASME-Journal of Basic Engineering,1960(3):35-45.

