深部巷道围岩变形相似模拟研究

郑文翔，胡耀青

(1.内蒙古科技大学 煤炭学院，内蒙古 包头 014010；2.太原理工大学 矿业工程学院，山西 太原 030024)

深部巷道围岩变形相似模拟研究

郑文翔1，2，胡耀青2

(1.内蒙古科技大学 煤炭学院，内蒙古 包头 014010；2.太原理工大学 矿业工程学院，山西 太原 030024)

针对深部围岩巷道变形和应力变化的特征，利用自制相似模拟实验平台，对无支护条件下的深部巷道的围岩破坏特征、围岩变形规律和围岩应力分布进行了定量和定性的研究，研究表明，深部巷道围岩具有大变形、大塑性区、应力集中程度高等特点，从而为类似地质条件下的巷道支护设计提供可靠的依据。

深部巷道；围岩破坏；应力变化；相似模拟

随着煤炭开采深度的增加，出现了许多与浅部开采不同的新问题和新特点，深埋巷道围岩与中浅部巷道不同点在于巷道开挖后围岩普遍处于不稳定的破裂状态[1-2]，表现出如岩层压力大、巷道位移量显著增加、支架损坏严重、巷道返修量剧增等问题，致使巷道维护变得非常困难[3-4]。相似模拟试验是矿业领域中一个重要的实验手段，其具有直观、经济，可靠性高等优点。本文利用自制相似模拟实验平台，对无支护条件下的深部巷道的围岩破坏特征、围岩变形规律和围岩应力分布进行了分析，对深部围岩巷道支护以及分区破裂化现象机理阐述等都具有一定的意义。

1 工程概况

本文以济宁地区万福煤矿回风大巷作为试验原型。巷道埋深900m，掘进断面高4m，宽5m，位于中砂岩中，平均单轴抗压强度约为75.9MPa，巷道顶板为灰黑色粉砂岩，厚度约5.4m，薄层状结构，致密，硬度大，硅质胶结，分选性较差，水平层理较发育，平均单轴抗压强度约为40.2MPa。巷道底板为灰黑色粉砂岩，厚度为4.3m，中厚层状结构，致密坚硬，硅质胶结，水平层理较发育，平均单轴抗压强度约为46.1MPa。

2 相似模型设计

自制的相似模拟实验平台如图1所示。

图1 相似模拟实验平台

2.1 相似材料配比

相似材料的配比是依据阜新矿业学院和淮南矿业学院所做的石灰、石膏相似材料配方试验成果[5-6]，选择试验相似材料的最佳配比和配方。

考虑到模型有效尺寸和煤层顶底板情况，确定模型的几个关键参数的比值[7-8]：

几何相似比选取a=30；容重相似比选取b=1.67；应力相似比选取c=50；时间相似比选取d=5.48。

2.2 试验测点布置

2.2.1 位移测点的布置

巷道围岩位移测点布置参数见表1，示意图见图2。

表1 测点布置参数

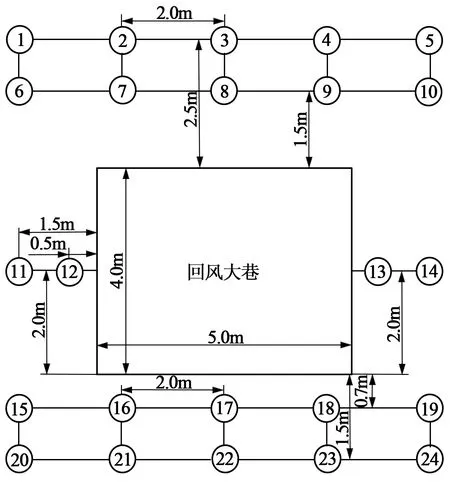
图2 位移测点布置

2.2.2 应力测点(应力盒)的布置

本次试验共安设了12个应力盒用来观测巷道围岩应力分布状态。巷道围岩应力测点布置参数见表2，示意图见图3。

表2 应力测点布置参数

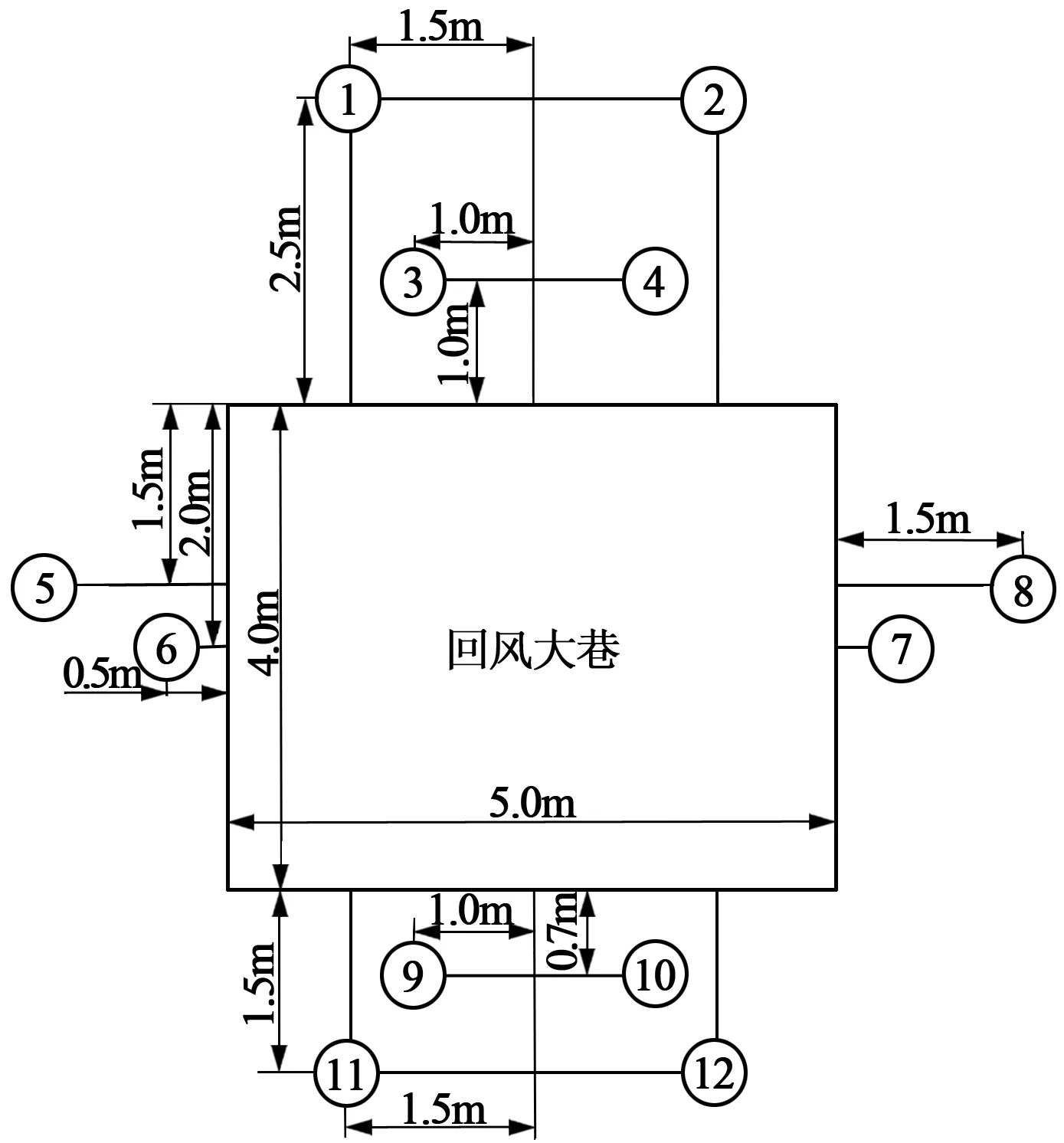
图3 应力测点布置

2.3 巷道加载和开挖巷道

2.3.1 加载

实验模型铺设完成后,就可以对模型进行加载,加载时要使顶部油缸和两侧油缸同步缓慢加载至设计好的加载值。

油缸供压值按下式进行计算:

式中，Q为油缸供压值，MPa；γ为未模拟上覆岩层容重，取0.025kN/m3；H为埋深，取900m；S为实验架砌块的横截面积，取0.261m2；α为相似实验应力相似常数，取50；S0为油虹活塞杆横截面积，取0.005042m2。

经计算得到油缸供压值Q=5.82MPa。水平方向油缸加载值取6.89MPa。对应的原型垂直应力为24.32MPa,水平应力为28.57MPa。

2.3.2 开挖巷道

相关设备安装和加载等程序完成后,即可进行巷道的开挖。打开模型架后面的开挖窗口,用钢板尺和自制开挖工具缓慢开挖巷道。

3 相似模型巷道围岩位移和应力分析

3.1 巷道围岩破坏宏观特征

实验过程中，保持垂直压力和水平压力不变，直至深部巷道在垂直应力和水平应力共同作用下产生破坏失稳。巷道围岩破坏情况为：深部巷道在无支护条件下，巷道顶板逐步破坏，并且最终形成冒落拱。巷道两帮随着开挖时间的变长，巷道开始发生严重内挤现象，并且局部出现剪切裂隙，底板同样存在剪切错动破坏现象，并伴随出现明显的底鼓现象。

3.2 巷道围岩位移分析

3.2.1 巷道顶板垂直位移分析

图4(a),(b)分别为距巷道顶板2.5m的第1排测点和距巷道顶板1.5m处的第2排测点的垂直位移随时间推移变化曲线图。巷道顶板随着时间增加而下沉量逐渐增加，但两排测点的位移却相差很大。图4(a)中的第1排测点的位移量均很小，位移量最大值为9.3mm。图4(b)中的第2排测点在第12d时巷道顶板下沉速率开始增加，在第42d后顶板变形开始稳定，此时顶板下沉量最大值197mm。随着距离巷道顶板表面的距离越近,测点位移越大,其中距巷道顶板表面2.5m处的测点位移极小，说明此处围岩变形对巷道几乎不产生影响，巷道顶板围岩塑性区深度小于2.5m。

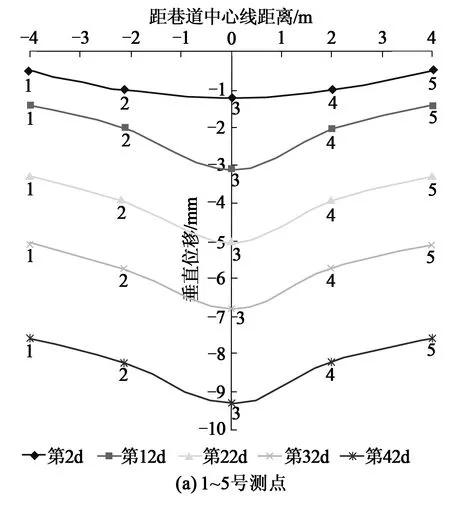
图4 巷道顶板不同层位围岩垂直位移

3.2.2 巷道两帮水平位移分析

图5(a)，(b)为巷道左右两帮中部测点11～14的水平位移曲线图。距巷帮0.5m处的测点12和测点13前12d内两帮移近速率比较快，12d后两帮变形速率放缓，在第42d后两帮变形开始稳定，此时左帮和右帮位移最大值分别为149mm和147mm。距巷帮1.5m处的测点11和测点14从开始观测到观测结束，测点的位移量均很小，位移量最大值分别为8.1mm和6.8mm。说明此处围岩变形对巷道几乎不产生影响，巷道两围岩塑性区深度小于1.5m。

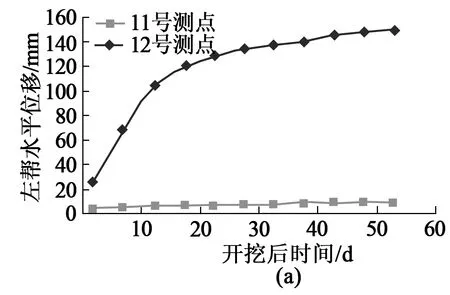
图5 巷道两帮不同部位围岩水平位移

3.2.3 巷道底板垂直位移分析

图6(a)、(b)分别为距巷道底板0.7m的测点和距巷道底板1.5m处测点的垂直位移随时间推移变化曲线图。巷道底板随着时间增加而向上鼓起，但各排测点的位移却相差很大。图6(b)中的测点20～24从开始观测到观测结束，测点的位移量均很小，位移量最大值为9.1mm。

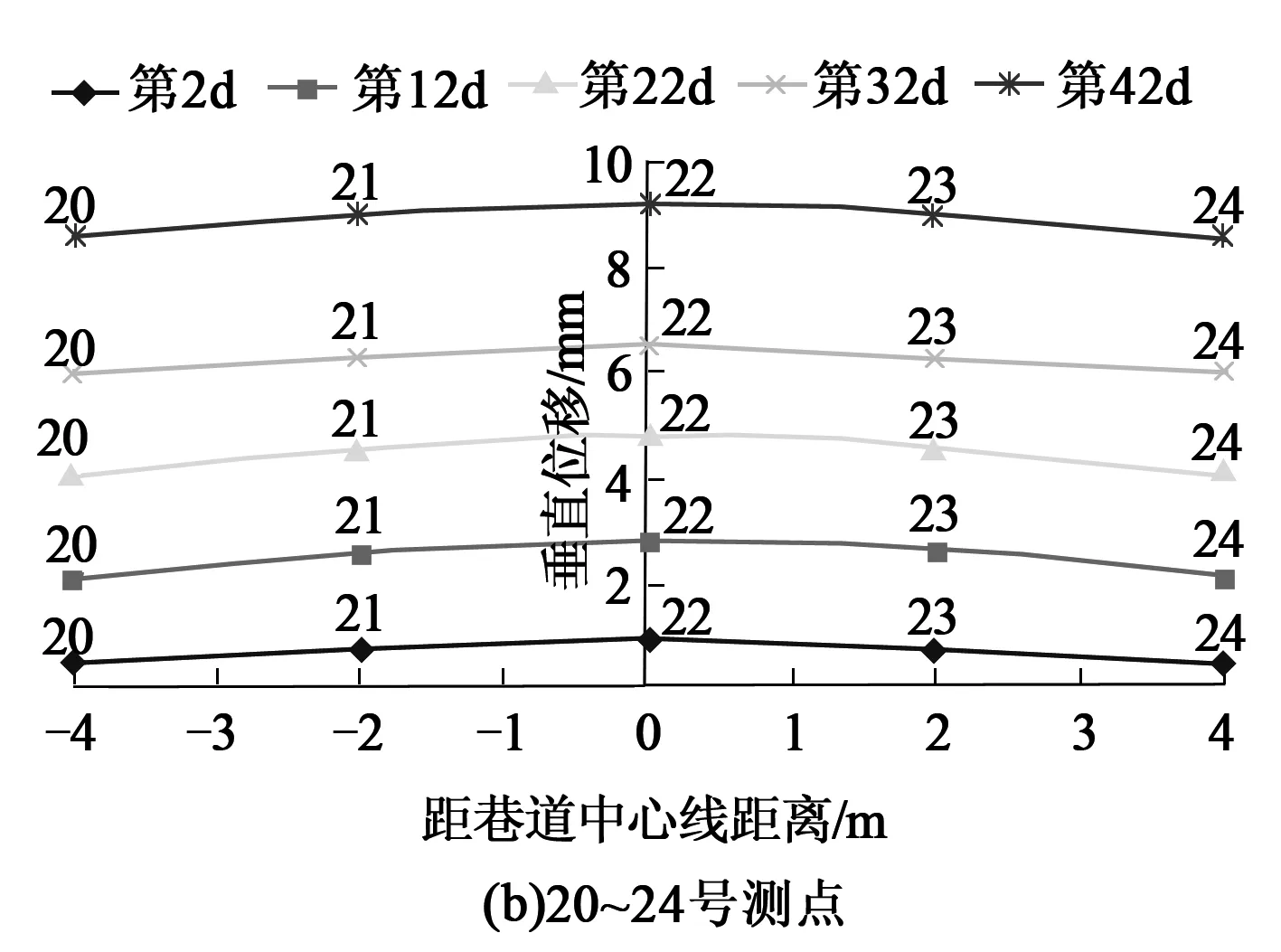
图6 巷道底板不同层位围岩垂直位移

图6(a)中的测点15～19前12d内巷道底鼓形势并不明显，在第12d时巷道底鼓速率开始增加，在第42d后底板变形开始稳定，此时底鼓量最大值157mm。并且从第22d开始，巷道底板右部位移开始明显大于底板左部，是因为底板发生了剪切错动。随着距离巷道底板表面的距离越近,测点位移越大，其中距巷道底板表面1.5m处的测点位移极小,说明此处围岩变形对巷道几乎不产生影响，巷道底板围岩塑性区深度小于1.5m。

3.3 巷道围岩应力分析

3.3.1 巷道顶板应力分析

图7(a)是距巷道顶板2.5m测点2和距巷道顶板1.0m测点4的垂直应力随时间变化的曲线，由于巷道临空面的卸载作用，顶板垂直应力集中程度不高。其中测点4随着时间的增加所受应力整体呈下降趋势，在前12d内下降速度最快，第12d后下降速率变缓，到第40d趋于稳定，到观测结束时所受应力值为3.21MPa。测点2距离巷道顶板表面较远，所受应力值大于测点4，但随着时间的增加整体也呈下降趋势，到观测结束时测点2应力值为10.21MPa。

图7(b)是距巷道顶板2.5m测点1和距巷道顶板1.0m测点3的水平应力随时间变化的曲线，其中测点3随着时间的增加所受应力整体呈下降趋势，前9d内下降速度最快，之后变缓最终趋于稳定，观测结束时水平应力值为8.14MPa。而测点1所受应力是先下降，在第9d后应力又缓慢增加，到观测结束时水平应力值达到35.21MPa，水平应力集中系数为1.26。可见测点3区域岩体已经发生破坏，应力向深部转移，测点1区域处于应力集中区域。

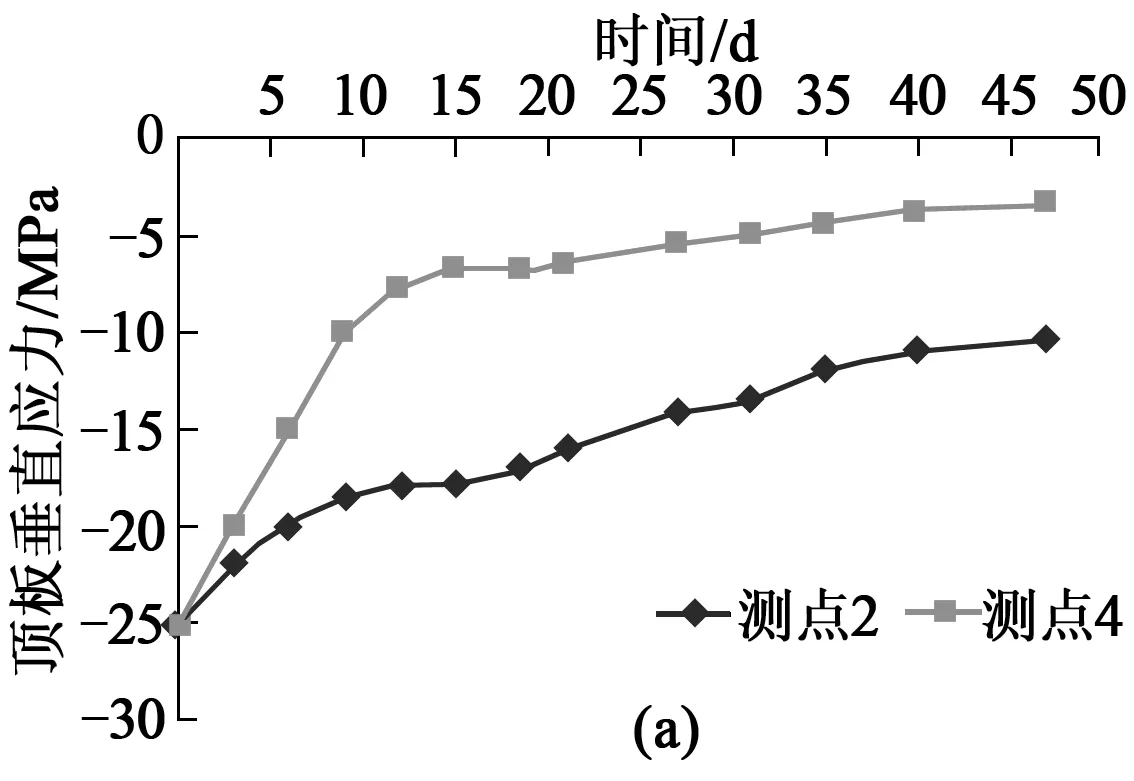
图7 巷道顶板垂直应力和水平应力与时间关系曲线

3.3.2 巷道两帮应力分析

图8(a)是巷道右帮测点7和测点8分别距巷道右帮表面0.5m和1.5m的垂直应力随时间变化的曲线，其中测点7随着时间的增加所受应力整体呈下降趋势，观测结束时所受垂直应力值为9.21MPa。而测点8所受应力在前9d内迅速下降，在第9d后应力又缓慢增加，到观测结束时测点所受垂直应力值达到39.81MPa，垂直应力集中系数为1.43。可见测点7区域岩体已经发生破坏，应力向深部转移，测点8区域处于应力集中区域。

图8(b)是巷道左帮测点6和5分别距巷道左帮表面0.5m和1.5m的水平应力随时间变化的曲线，其中测点6随着时间的增加所受应力整体呈下降趋势，在前12d内下降速度最快，第12d后下降速率变缓，到观测结束时所受应力接近为0。测点5距离巷道顶板表面较远，所受应力值大于测点6，但随着时间的增加也是整体呈下降趋势，到观测结束时测点5所受应力值为7.19MPa。

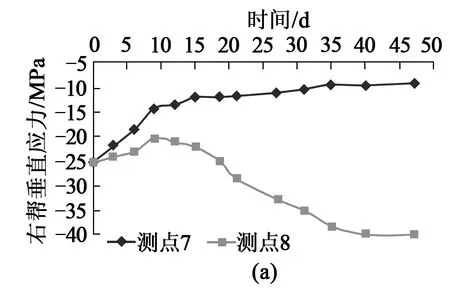
图8 巷道两帮垂直应力和水平应力与时间关系曲线

3.3.3 巷道底板应力分析

图9(a)是巷道底板测点10和12分别距巷道底板表面0.7m和1.5m的垂直应力随时间变化的曲线，由于巷道临空面的卸载作用，巷道底板垂直应力集中程度比较低。测点10和测点12随着时间的增长整体呈下降的趋势,下降速度开始快，后来变慢，最终趋于稳定，到观测结束时，测点10垂直应力接近为0，测点12垂直应力值为7.89MPa。

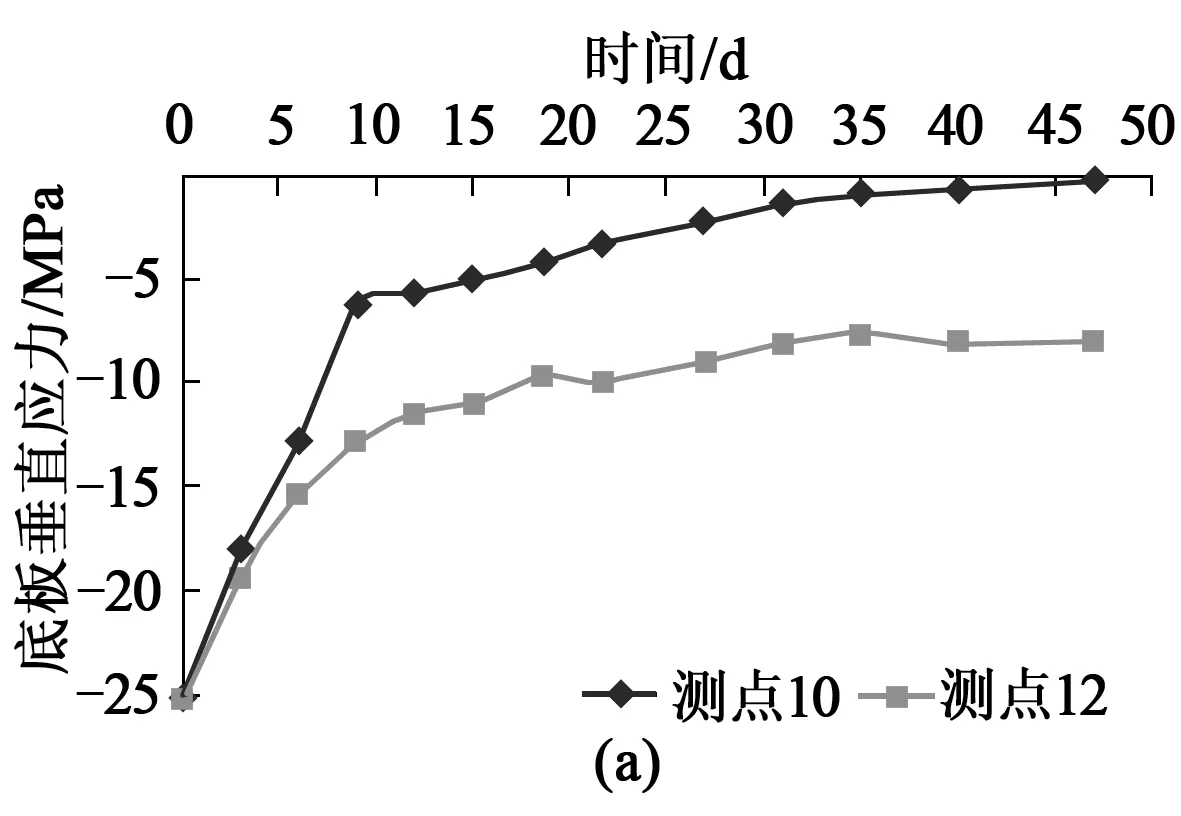
图9 巷道底板垂直应力和水平应力与时间关系曲线

图9(b)是巷道底板测点9和11分别距巷道底板表面0.7m和1.5m的水平应力随时间变化的曲线，随着时间的增长，测点9应力值是整体下降的趋势。观测结束时所受水平应力值为7.13MPa。测点11在前9d内应力逐渐下降，9d后应力又逐渐增加，到观测结束时所受水平应力值为33.48MPa，水平应力集中系数为1.21。可见测点9区域岩体已经发生破坏，应力向深部转移，测点11区域处于应力集中区域。

4 结论

通过采用相似模拟实验研究手段，对深部巷道开挖的围岩破坏特征、位移变化规律和应力变化规律进行了试验分析，结论如下：

(1)深部巷道在无支护条件下，巷道顶板形成冒落拱，巷道两帮发生严重内挤现象，局部出现剪切裂隙，底板剪切错动破坏，出现明显的底鼓现象。

(2)随着距离巷道表面的距离越近，测点位移量越大，且随着时间的增长，测点位移速率开始增加，达到一定时间后变形开始稳定。距顶板1.5m处位移测点最大下沉量为197mm；距巷帮0.5m处位移测点观测，两帮最大移近量为296mm；距底板0.7m处位移测点观测，底鼓量最大值为157mm；测点位移量极小说明此处围岩变形对巷道几乎不产生影响，从而确定围岩塑性区的深度，巷道顶板、两帮和底板塑性破坏深度分别小于2.5m、1.5m和1.5m左右。

(3)随着时间的增长巷道顶底板测点所受垂直应力表现为整体呈下降趋势，开始下降速度快，后来变缓，最终趋于稳定；距巷道表面较近的测点所受水平应力表现为开始整体呈下降趋势，之后变缓最终趋于稳定，而距巷道表面较远的测点所受水平应力表现为先下降，后来应力又缓和增加，到结束时应力达到最大值，顶板2.5m处水平应力集中系数为1.26，底板1.5m处水平应力集中系数为1.21。

(4)随着时间的增长巷道两帮距巷道表面较近的测点所受垂直应力表现为整体呈下降趋势，之后变缓最终趋于稳定，距巷道表面较远的测点所受垂直应力表现为先下降，后来应力又缓和增加，到结束时应力达到最大值，两帮1.5m处垂直应力集中系数为1.43。巷道两帮的各测点所受水平应力表现为开始整体呈下降趋势，之后变缓最终趋于稳定。

[1]靖洪文，李元海，许国安.深埋巷道围岩稳定性分析与控制技术研究[J].岩土力学，2005,26(6):877-880.

[2]何满潮，谢和平，彭苏萍，等.深部开采岩体力学研究[J].岩石力学与工程学报，2005，24(16)：2803-2813.

[3]李 杰，宋春明，等.深部巷道围岩变形破坏机制分析[J].岩石力学，2012，33(2)：365-366.

[4]靖洪文，吴俊浩，马 波，等.基于模糊灰色系统的深部巷道围岩变形预测模型及应用[J].煤炭学报，2012，37(7)：1099-1100.

[5]李晓红.岩石力学实验模拟技术[M].北京：科学出版社，2006.

[6]康希并，张建义.相似材料模拟中的材料配比[J].淮南矿业学院学报，1988(1)：50-18.

[7]朱维申，张玉军，任伟中.系统锚杆对三峡船闸高边坡岩体加固作用的块体相似模型试验研究[J].岩土力学，1996，17(2)：1-6.

[8]刘 钦.软岩隧道大变形机制与控制对策及其应用研究[D].济南：山东大学，2011.

[责任编辑：林健]

AnalogueSimulationofSurroundingRockDeformationinDeepRoadway

ZHENG Wen-xiang1,2,HU Yao-qing2

(1.Coal School,Inner Mongolian University of Science & Technology,Baotou 014010,China;2.Mining Engineering School,Taiyuan Technology University,Taiyuan 030024,China)

Applying self-made analogue simulation platform,characteristic of surrounding rock failure,deformation and stress distribution in deep roadway were researched quantificationally and qualitatively.Results showed that deep roadway had the characteristics of large deformation,large plastic zone and high stress concentration,which provided reference for supporting design of roadway with similar condition.

deep roadway; surrounding rock failure; stress variation; analogue simulation

2014-01-24

10.13532/j.cnki.cn11-3677/td.2014.05.019

郑文翔(1979-)，男，山西山阴人，讲师，硕士研究生，主要从事煤矿开采技术、井巷支护、矿山压力等方面的研究。

郑文翔，胡耀青.深部巷道围岩变形相似模拟研究[J].煤矿开采，2014，19(5)：65-69.

TD32

A

1006-6225(2014)05-0065-05