单砂体内部物性参数解释模型的建立方法研究

杨东瑞雪

（中石油大庆油田有限责任公司第七采油厂，黑龙江 大庆 163517）

B断块位于A构造东北翼，东西两侧为近南北向的封闭性大断层所分隔，南端为近东西向断层所分隔，整体上构造呈近南北向展布，是一个西高东低的断块构造，断块内部大断层不发育，小断层呈零星分布。B断块开发对象为PI油层组，埋藏深度800～1000m，位于白垩系姚家组一段，沉积背景处于松辽盆地北部大型河流－三角洲沉积体系大庆长垣南部三角洲前缘相带内，具浅水、枝状的特点。受大庆长垣三角洲北部物源的控制，砂体展布总趋势为自北向南，同时受河湖双重作用影响，砂体呈片状、条带状、断续条带状及透镜体或零星分布。下面，笔者以A油田B断块为例，在前期地质研究成果基础上，通过标准化测井曲线基础上开展单砂体内部结构单元物性参数的求取，描述单砂体内部物性变化规律，探讨了适合建立低渗透储层单砂体内部物性参数模型的方法。

1 泥质含量计算

泥质含量是描述储层岩性特征的主要参数，其计算结果直接关系到孔隙度、渗透率的计算结果。自然电位、自然伽马曲线反映泥质含量，由于自然伽马测井曲线比较少，而所有井都有自然电位曲线［1］，因此采用自然电位计算泥质含量VSH :

式中，ΔSP为自然电位测井相对值，mV；SP为自然电位测井值，mV，SPmax为纯泥岩处的自然电位测井值，mV；SPmin为纯砂岩处的自然电位测井值；VSH 为泥质含量；GCCUR为希尔奇指数，对第三纪地层为3.7，对老地层为2。

2 孔隙度计算

2.1 有声波时差曲线的井

对于有声波时差曲线的井，孔隙度的计算一般采用通用公式——威利公式:

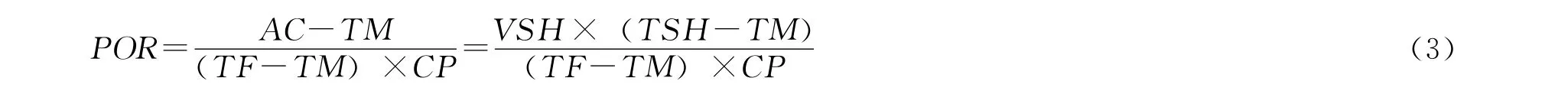
式中，POR为地层孔隙度；TM 为骨架时差，μm／s；TF为流体时差，μm／s；TSH 为泥岩时差，μm／s；CP为压实校正系数；AC为声波时差，μm／s。

由于埋藏浅，泥质胶结砂岩未压实，岩石颗粒不能紧密接触，使声波旅行时间增大，利用公式计算就会偏高，需要进行压实校正，一般泥岩时差大于328μm／s，压实系数CP＝TSH／328。而对于泥岩时差的选取需要根据每口井的声波时差曲线进行读取，根据微电极曲线和自然电位曲线判断泥岩段位置，对应泥岩段的声波时差曲线即为泥岩时差［2］。

2.2 缺少声波时差曲线的井

由于研究区内部分井缺少声波时差曲线，无法利用威利公式求取孔隙度。此时从其他测井曲线出发，对已求取出孔隙度的井进行孔隙度与测井曲线相关性分析，选取相关性较大的参数进行回归，从而求取缺少声波时差曲线的这部分井的孔隙度。

表1是孔隙度与各参数的相关性分析表。从表1中可以看出，lg（R025）、lg（R045）、VSH 与孔隙度相关性最大，所以选用这3个参数进行回归分析，建立孔隙度模型:

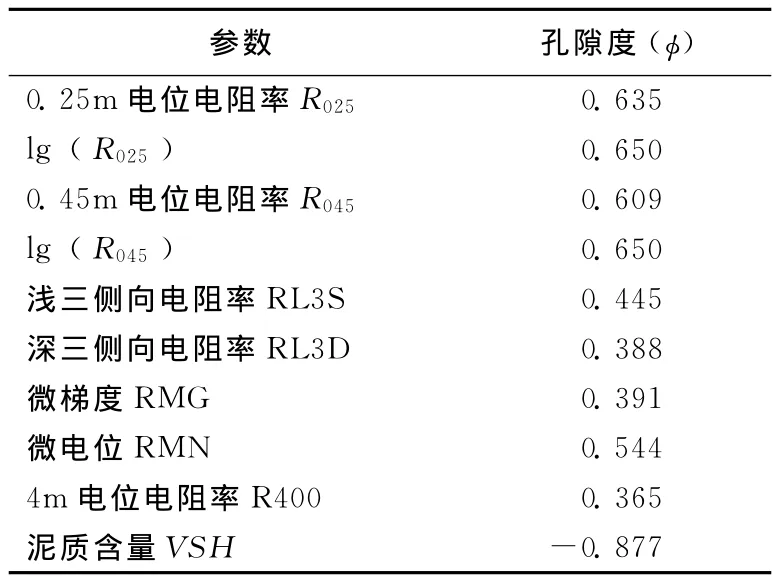
表1 孔隙度 （φ）与各参数的相关性

式中，R025为0.25m电阻率，Ω·m；R045为0.45m电阻率，Ω·m。

3 渗透率计算

根据A油田探井及检查井资料进行渗透率（K）与泥质含量、孔隙度之间的相关性分析，因为渗透率的变化范围大，所以将其取对数后作为参数输入。从分析结果 （见表2）可以看出，渗透率和孔隙度 （φ）的相关性最大。

基于泥质含量、孔隙度等与渗透率的相关性分析结果，通过数理统计软件进行回归，从而建立储层渗透率的计算模型:

表2 渗透率与泥质含量、孔隙度的相关性

4 物性参数解释模型的检验

首先应用上面建立的物性参数解释模型求取检查井的参数值，再与检查井原始参数值进行对比分析，如图1、图2所示。孔隙度平均误差为7.58%，空气渗透率平均误差为14.15%，误差均不超过15%，可知笔者研究所建立的物性参数解释模型比较准确、合理。

图1 检查井原始孔隙度与模型计算孔隙度对比

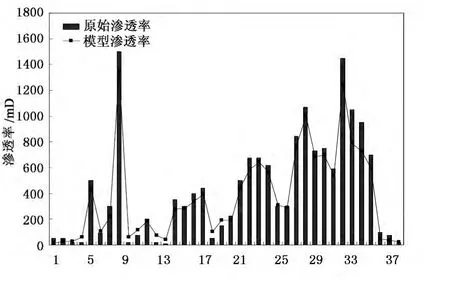
图2 检查井原始渗透率与模型计算渗透率对比

X井原始模型求取渗透率与研究求取渗透率数值对比如图3所示。从图3可以看出，X井原始模型计算的渗透率变化幅度较小，数值较接近，纵向上解释精度不足，不利于研究储层非均质性。研究建立的渗透率模型求取的渗透率变化幅度较大，解释精度较细，解释结果比较符合葡北油田及葡北三断块实际的储层特征，能够更加准确地体现储层的非均质性。

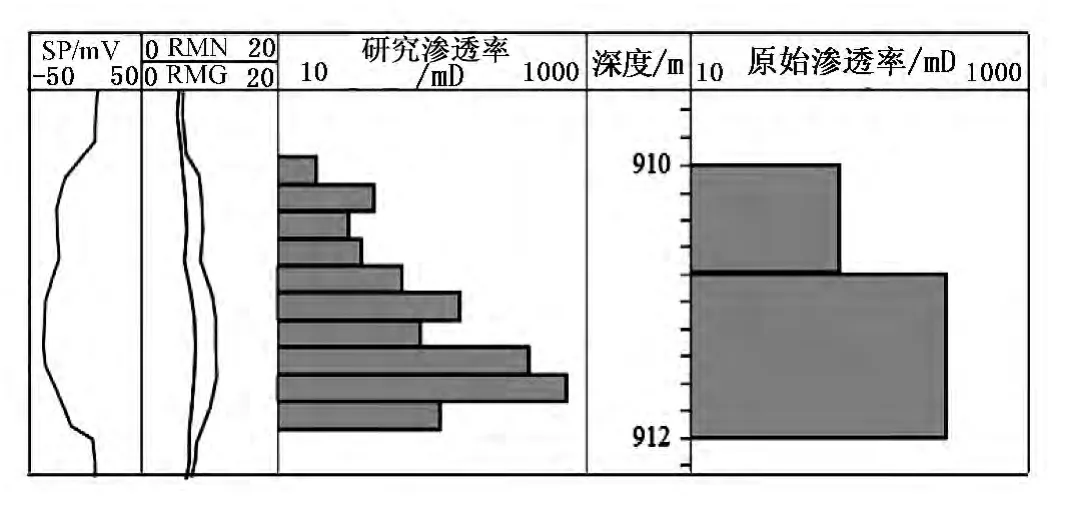
图3 X井原始模型求取渗透率与研究求取渗透率数值对比

5 结论

1）物性参数解释模型的解释结果较为可靠、合理，误差均不超过15%。

2）研究建立的物性参数解释模型求取的物性参数解释精度较高，能够达到纵向上0.25m的精度，解释结果比较符合A油田及B断块实际的储层特征，能够更加准确地体现储层的非均质性。

［1］王冬焕，黄思静 .单砂体建模技术及应用—以华北油田某区块为例 ［J］.岩性油气藏，2012，24（4）:93－98.

［2］郭大立，曾晓慧，江茂泽 .计算各向异性岩心渗透率的方法研究 ［J］.水动力学研究与进展 （A辑），2004（1）:23－25.