自调整的捕鱼策略优化算法*
李景洋,王 勇,李春雷
(1.广西民族大学信息科学与工程学院,广西 南宁 530006;2 南宁市环境保护监测站,广西 南宁 530012;3.南宁供电局,广西 南宁 530031)
自调整的捕鱼策略优化算法*
李景洋1,2,王 勇1,李春雷3
(1.广西民族大学信息科学与工程学院,广西 南宁 530006;2 南宁市环境保护监测站,广西 南宁 530012;3.南宁供电局,广西 南宁 530031)
针对基本捕鱼策略优化算法(FSOA)在优化过程中存在易陷入局部最优、求解高维的复杂优化问题时优化性能不好的不足,对基本捕鱼策略优化算法(FSOA)进行了改进,提出了自调整的捕鱼策略优化算法(ADFSOA):算法采用时变的搜索半径,每个渔夫可根据自己所处的状态自我调整搜索策略。通过与基本FSOA、RFSOA和标准PSO算法的数值实验对比, 表明了所提算法的优化性能具有显著的优势,可用于求解高维的复杂优化问题。
捕鱼策略优化算法(FSOA);ADFSOA;时变搜索半径;调整因子
1 引言
20世纪70年代,遗传算法[1]的提出开启了求解全局优化问题的新纪元。在过去的30年里,群智能算法得到了越来越多的关注。许多受生物学启发的算法被陆续提出来[2~11]。大自然是提出新的元启发式算法的重要灵感来源,仿生算法是受自然启发的元启发式算法的一个重要策略。如:蚁群算法[2]源于对自然界蚂蚁觅食行为的模拟;粒子群算法[3]源自对鸟群为了寻找食物和保护群体所特有的行为的模拟;人工鱼群算法[4]是受鱼群的觅食行为、追尾行为和聚群行为启发而提出的。而相比鸟、蚂蚁、鱼以及其他昆虫,人类具有更高的智能。文献[12]通过对现实世界中渔夫的捕鱼行为的模拟,提出了一种采用捕鱼策略的优化方法FSOA(Fishing Strategy Optimization Algorithm)。该算法具有理论方法简单、设置参数少、易于编码实现的优点。但是,同时也存在一些不足,主要表现为:(1)算法搜索缺乏随机性,降低了算法的搜索效率;(2)针对高维的复杂优化问题,其优化能力比较差,易陷入局部极值。针对基本FSOA存在的不足,文献[13~16]从不同的角度对基本FSOA进行了改进。文献[13]提出采用正交变换确定探测点的改进方法,文献[14]提出将FSOA与PSO相结合的优化方法,文献[15,16]提出采用随机动态选择探测点的改进方法。尽管文献[13~16]所提出的改进方法在一定程度上提高了算法的搜索效率,但面对高维的复杂优化问题仍显得力不从心,仍无法用来解决高维的复杂优化问题,未能从根本上提高算法的优化能力。
针对以上仍存在的不足,本文提出了一种自调整的捕鱼策略优化算法ADFSOA(ADjustive Fishing Strategy Optimization Algorithm):不使用收缩搜索策略,而是采用自我调整搜索策略,搜索者根据自己所处的状态来调整搜索方法。
2 基本FSOA介绍
在基本FSOA中,渔夫采用移动搜索与收缩搜索相结合的搜索策略,以“方体”格式确定探测点。具体方法如下:

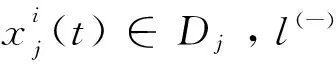
其中,α(0<α<1)称为收缩因子。然后按前面的方法来确定Ω(Xi(t+1))中是否有比Xi(t+1)更优的点。按这样的方法展开搜索,称之为收缩搜索。
说明:(1)算法设有公告板。公告板是记录最优渔夫个体状态的地方。每个渔夫将自己当前状态与公告板中记录进行比较,若优于公告板中的记录,则用自身状态更新公告板中的记录,否则公告板的记录不变;(2)算法设有在同一点处可进行收缩搜索次数的最大阈值。若某渔夫在某点处进行收缩搜索次数达到了最大阈值,但其状态仍未发生改变,该渔夫则要在打鱼作业区中重新随机选点。
3 改进的捕鱼策略优化算法
3.1 搜索行为描述
人类是自然界智能最高的行为主体,人类可依据周围环境的变化不断地调整自身状态和行为策略,以更好地适应环境;人类有向他人学习、以克服自身存在之不足的天性。渔夫出海打鱼,都希望能在较短的时间内找到水域中鱼浓度最大的区域或位置,以期能捕获更多的鱼。渔夫根据周围鱼浓度的变化和群体状况来不断地调整自己的位置和行动策略。据此,本文提出的算法采用如下策略:(1)渔夫采用动态搜索方式。前期采取较大的搜索半径,以期能尽快搜索到鱼浓度比较高的区域。随着搜索时间的增加,渔夫越来越有可能找到或靠近鱼密度比较高的位置或区域,因而要逐渐缩小搜索范围(缩小搜索半径),以期找到鱼密度最高的位置。(2)以自我调整机制代替收缩机制。渔夫在当前位置搜索失败后(即未搜索到鱼浓度高于当前自己所在的位置的鱼浓度),渔夫则根据自己当前在群体中的优劣顺序来调整其下一步的行为,调整自己的行动策略,以期尽快找到更好的捕鱼区域或位置。

(1)搜索半径是时变的。在搜索过程中,渔夫的搜索半径l是时间t的函数,其变化规律按如公式(1)所示:
(1)

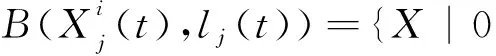
(2)
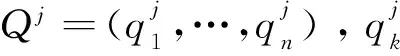
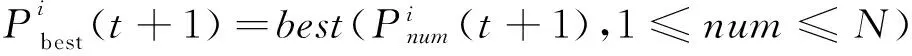
Case1若si(t)=1,即渔夫i处于当前群体最优位置,则下一步将按公式(1)和公式(2),在B(Xi(t),l(t+1))中继续进行移动搜索,并记Xi(t+1)=Xi(t)。
Case2若si(t)≠1,渔夫i则根据公式(3)来确定其自我调整因子AFi(t)(Adjustive Factor),并根据公式(4)来确定其调整策略:
(3)
(4)
其中,r、α均为(0,1)中均匀分布的随机数,k为{1,…,n}中的一个随机整数。也就是说,渔夫依据自我调整因子AFi(t)来确定其下一步的捕鱼策略:处于鱼浓度比较高的位置的渔夫倾向于以换维的方式向最优渔夫靠近,即其j维换到最优渔夫的第k维,而处于适应度比较差的位置的渔夫倾向于向最优渔夫移动。
3.2 算法实施步骤:
算法ADFSOA

输出:最优渔夫所在位置及所在位置鱼的浓度。
步骤1初始化:在可行域内随机生成M个渔夫,记录群体最优渔夫所在的位置,评价渔夫所在位置鱼的浓度,t←1
步骤2渔夫按公式(1)计算搜索半径。
步骤3对渔夫i(i=1,…,M)执行以下操作:
步骤3.1按公式(2)在搜索域内选取N个探测点。
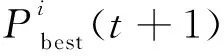
步骤3.3将所有渔夫按适应度从优到劣进行排序,以si(t)表示渔夫i的序号,若si(t)=1,则执行步骤3.3.1,否则执行步骤3.3.2;
步骤3.3.1渔夫位置不变,即Xi(t+1)= Xi(t),转步骤3.1;
步骤3.3.2根据公式(3)计算调整因子AFi(t),根据公式(4)来确定自己的行动策略,改变位置。
步骤3.4记录当前最优渔夫所在的位置。
步骤4t←t+1,判断算法是否达到终止条件,若是则转至步骤5,否则转步骤2。
步骤5输出最优渔夫所在位置及所在位置鱼的浓度,运行结束。
4 实验仿真与结果分析
4.1 测试函数
为了验证本文提出的ADFSOA算法的有效性,我们将ADFSOA算法与FSOA、PSO、RFSOA[16]进行数值实验对比。本文选择以下六个基准测试函数进行数值实验测试分析:
(1)Schwefel’sproblem2.12:
该函数在点(0,0,…,0)处取得全局极小值0。
(2)Ackley’s function:
该函数在点(0,0,…,0)处取得全局极小值0。
(3) Rastrigin’s function:
该函数在点(0,0,…,0)处取得全局极小值0。
(4) Griewank’s function:
该函数在点(0,0,…,0)处取得全局极小值0。
(5) Sphere function:
该函数在点(0,0,…,0)处取得全局极小值0。
(6) Step function:
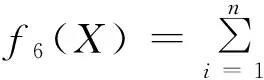
该函数在-0.5≤xi≤0.5处取得全局极小值0。
4.2 数值实验仿真
本次实验使用的计算机为AMD Phenom(tm)ⅡP820、2 GB内存的PC机;编程软件为Matlab2010a。
为了避免随机性对实验结果的影响,每一种算法针对每个函数均独立运行50次,并求最优值、最差值、平均值、标准差、平均迭代次数以及50次优化测试中找到精确解的次数。本文得到的实验结果如表1所示。
为了能更明显地对比出各种算法的优化性能,我们给出了这六个测试函数的收敛曲线仿真图。如图1~图6所示。
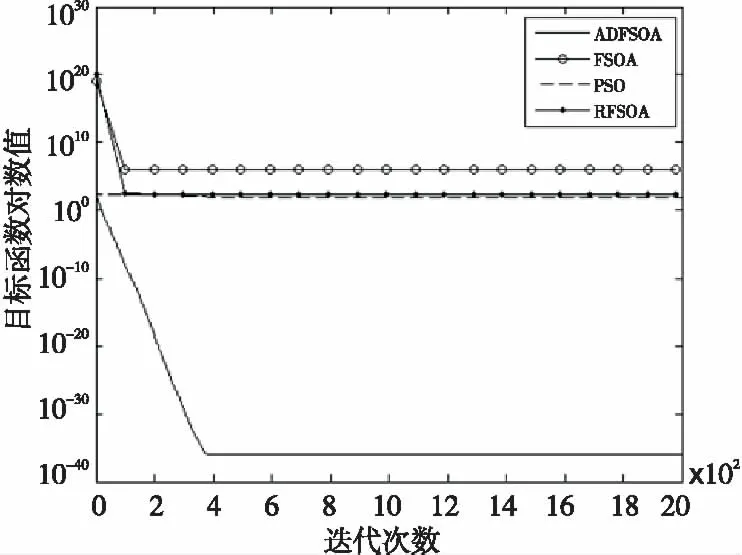
Figure 1 Comparison of convergence curve f1(X)图1 函数f1(X)收敛曲线对比图

Figure 2 Comparison of convergence curve f2(X)图2 函数f2(X)收敛曲线对比图
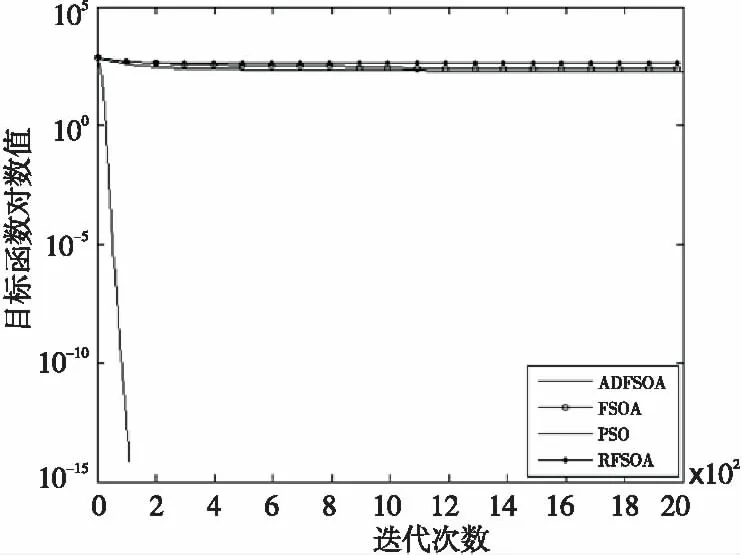
Figure 3 Comparison of convergence curve f3(X)图3 函数f3(X)收敛曲线对比图
实验结果分析:(1)从表1中的“找到精确解的
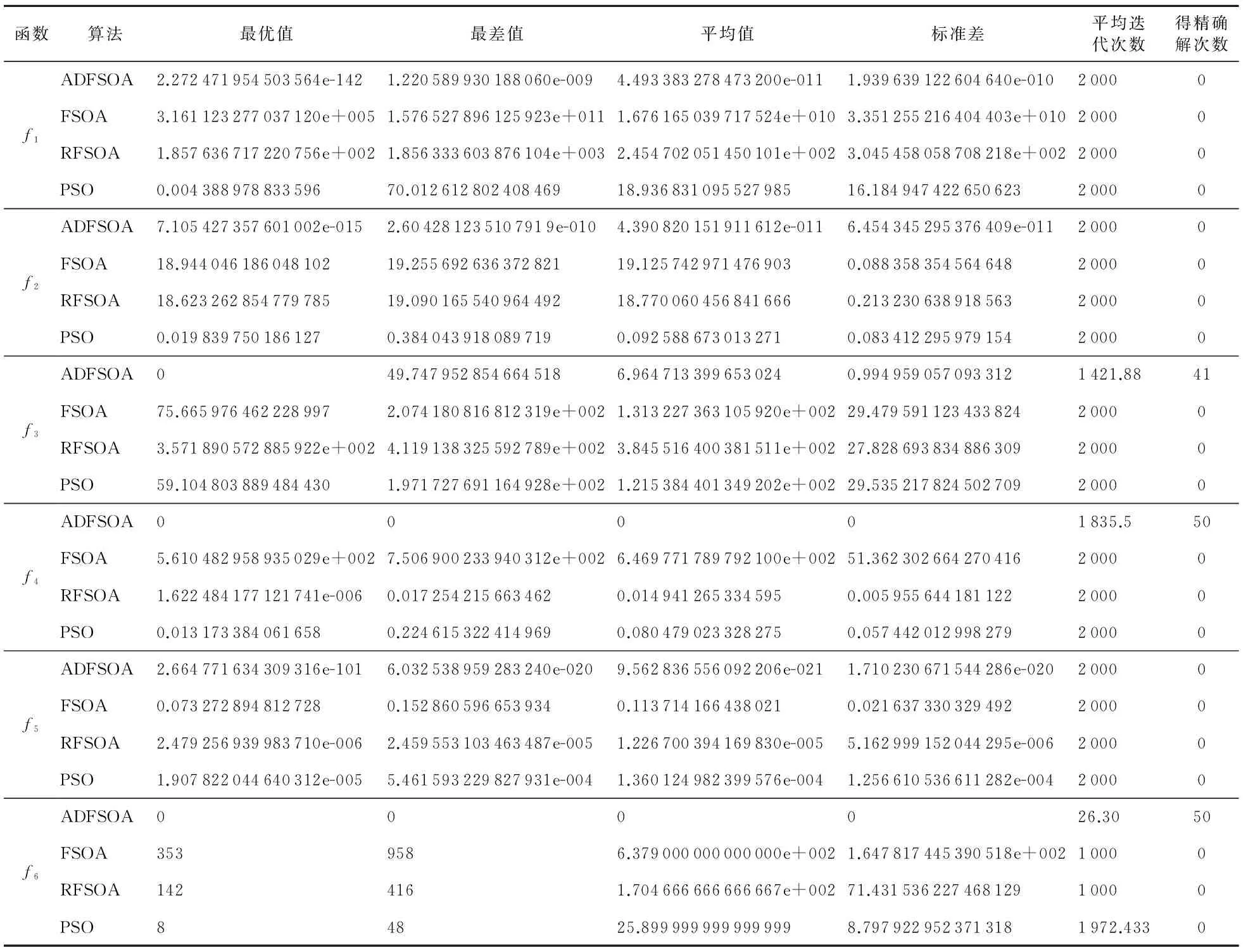
Table 1 Experimental results
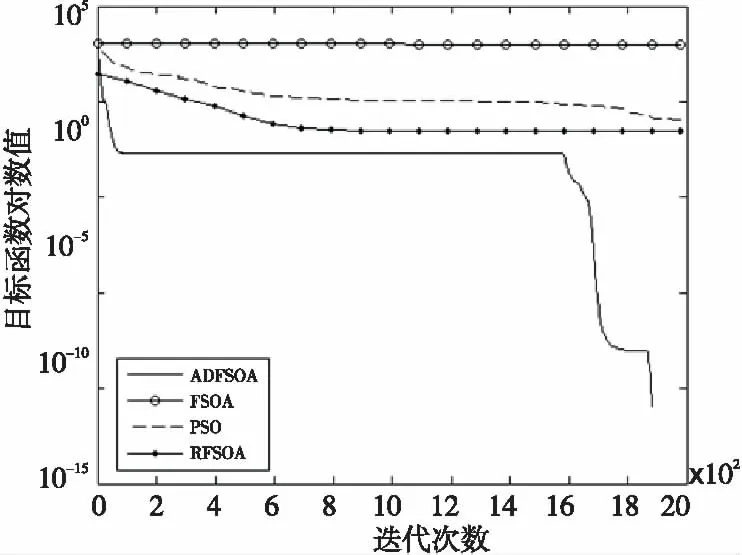
Figure 4 Comparison of convergence curve f4(X)图4 函数f4(X)收敛曲线对比图
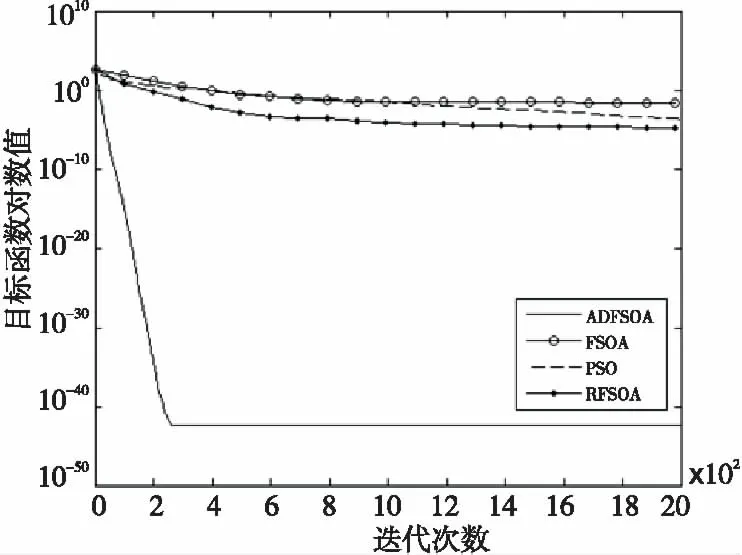
Figure 5 Comparison of convergence curve f5(X)图5 函数f5(X)收敛曲线对比图

Figure 6 Comparison of convergence curve f6(X)图6 函数f6(X)收敛曲线对比图
次数”指标上看,在这50次的优化测试中,ADFSOA能以较大的概率找到函数f3、f4和f6的全局最优点,基本的PSO、 RFSOA和FSOA均没有找到这些函数的全局最优点。(2)从表1中的“最优值”、“最差值”、“平均值”、“标准差”、“平均迭代次数”这几项评价指标上看,ADFSOA的优化性能明显优于基本FSOA、RFSOA和标准PSO。(3)从收敛曲线对比图1~图6中可以看出,ADFSOA的收敛速度明显比基本FSOA、RFSOA和标准PSO都快。
5 结束语
针对基本FSOA在处理复杂优化问题中容易陷入局部极值、求解高维的复杂优化问题时优化性能不太好的不足,提出了一种自调整的捕鱼策略优化算法。实验结果表明,本文提出的算法能有效地克服基本FSOA难以克服的易陷入局部最优的问题;而对于高维的复杂优化问题,本文算法的优化性能良好,其优化性能均比基本FSOA、现有的改进FSOA以及标准PSO算法好。
[1] Holland J H.Adaptation in nature and artificial systems[M]. CA,MA:MIT Press, 1992.
[2] Dorigo M, Birattari M, Stüzle T. Ant colony optimization:Artificial ants as a computational intelligence technique[J]. IEEE Computing Intelligence Magazine, 2006, 1(4):28-39.
[3] Kennedy J, Eberhart R C. Particle swarm optimization[C]∥Proc of the IEEE International Conference on Neural Networks, 1995:1942-1948.
[4] Li Xiao-lei,Shao Zhi-jing,Qian Ji-xin.An optimizing method based on autonomous animals:Fish-swarm algorithm[J]. Systems Engineering Theory and Practice, 2002, 22(11):32-38.
[5] Jiao L C,Wang L. A novel genetic algorithm based on immunity[J].IEEE Transactions on System, Man and Cybernetic,2000,30(5):552-561.
[6] Oftadeh R, Mahjoob M J, Sharitatpanahi M. A novel meta-heuristic optimization algorithm inspired by group hunting of animals:Hunting search[J].Computer and Mathematics with Applications, 2010,60:2087-2098.
[7] Dai C,Chen W,Song Y,et al. Seeker optimization algorithm:A novel stochastic search algorithm for global numerical optimization[J].Journal of Systems Engineering and Electronics, 2010,21(2):300-311.
[8] Yang X-S. Firefly algorithm, Lévy flights and global optimization[M]∥Reaserch and developments in intelligent systemsXXVI. London:Springer-Verlag, 2010:209-218.
[9] Yang X-S, Deb S. Cuckoo search via Lévy flights[C]∥Proc of the World Congress on Nature & Biologically Inspired Computing (NaBIC 2009),2009:210-214.
[10] Yang X-S. A new metaheuristic bat-inspired algorithm[C]∥Proc of Nature Inspired Cooperative Strategies for Optimization NISCO, 2010:65-74.
[11] Passino K M. Biomimicry of bacterial foraging for distributed optimization[M].NJ:Princeton:University Press, 2001.
[12] Chen Jian-rong, Wang Yong. Optimization approach on using fishing stragety[J].Computer Engineering and Applications,2009,45(9):53-56.(in Chinese)
[13] Wang Yong, He De-niu, Guan Yi-jun, et al. An improving FSOA optimization by using orthogonal transform[C]∥Proc of the International Conference on Electronic Commerce,Web Application, and Communication, 2011:63-69.
[14] Pang Xing, Wang Yong. Optimization approach combined PSO with fishing strategy[J].Computer Engineering and Applications,2011,47(8):36-40.(in Chinese)
[15] Chen Shi-liang, Wang Yong, Chen Jian-rong. Improved FSOA by using random detection strategy[J]. Computer Engineering and Applications,2011,47(26):49-52.(in Chinese)
[16] He De-niu,Wang Yong, Guan Yi-jun. Improved FSOA by using random detecting[J]. Computer Engineering and Applications 2011, 47(36):44-46.(in Chinese)
附中文参考文献:
[12] 陈建荣,王勇.采用捕鱼策略的优化方法[J]. 计算机工程与应用,2009, 45(9):53-56.
[14] 庞兴,王勇.PSO与捕鱼策略相结合的优化方法[J]. 计算机工程与应用, 2011, 47(8):36-40.
[15] 陈士亮, 王勇, 陈建荣.一种采用随机探测策略的改进FSOA[J]. 计算机工程与应用, 2011, 47(26):49-52.
[16] 何德牛,王勇,管忆军.采用随机探测的改进FSOA[J]. 计算机工程与应用, 2011, 47(36):44-46.
LIJing-yang,born in 1989,MS,her research interest includes computational intelligence.

王勇(1963-),男,广西南宁人,博士,教授,研究方向为计算智能和数据挖掘。E-mail:wangygxnn@sina.com
WANGYong,born in 1963,PhD,professor,his research interests include computational intelligence, and data mining.

李春雷(1987-),男,河南信阳人,硕士,研究方向为智能计算、电力系统保护与控制。E-mail:lichunlei0218@126.com
LIChun-lei,born in 1987,MS,his research interests include computational intelligence, power system protection and control.
Adjustivefishingstrategyoptimizationalgorithm
LI Jing-yang1,2,WANG Yong1,LI Chun-lei3
(1.College of Information Science and Engineering,Guangxi University for Nationalities,Nanning 530006;2.Environmental Protection Monitoring Station of Nanning,Nanning 530012;3.Nanning Power Supply Bureaus,Nanning 530031,China)
In order to overcome the shortcomings that basic FSOA is easily trapped in local optimum and unable to solve the high-dimensional complex optimization problems,an improved FSOA,named ADjustive Fishing Strategy Optimization Algorithm (ADFSOA),is proposed.In the algorithm,every fisherman (searcher) uses a time-varying search-radius and can adjust his searching strategy according to his own state.Numerical experiments show that,compared with basic FSOA,RFSOA and standard PSO,the proposed algorithm is much superior to other algorithms and can be used to solve the complex high-dimensional optimization problems.
FSOA;ADFSOA;time-varying search radius;adjustive factor
1007-130X(2014)05-0923-06
2012-10-22;
:2013-01-21
国家自然科学基金资助项目(61074185);广西自然科学基金资助项目(0832084);广西高等学校科研项目(201202ZD032)
TP18
:A
10.3969/j.issn.1007-130X.2014.05.023

李景洋(1989-),女,河南漯河人,硕士,研究方向为计算智能。E-mail:miaolianjingyang@126.com
通信地址:530006 广西南宁市广西民族大学信息科学与工程学院
Address:College of Information Science and Engineering,Guangxi University for Nationalities,Nanning 530006,Guangxi,P.R.China

