粉末注射成形的离散元模拟实验研究

刘 煜，李益民，夏卿坤，何 浩，胡幼华

（1中南大学 粉末冶金国家重点实验室，长沙410083；2长沙学院 机电工程系，长沙 410022）

粉末注射成形是一种适合于小型复杂零部件批量制备的近净成形技术，其成品缺陷基本是在注射成形过程中形成，如粉末密度分布不均、欠注、裂纹、孔隙、焊接线、粉末与黏结剂两相分离现象等，这些缺陷在脱脂和烧结后，通常又会导致变形、开裂、不规则收缩、水泡及翘曲等不良后果［1，2］。在注射成形阶段是无法通过简单的观察和测量来检测和控制的，因此对粉末微注射成形喂料充模机理的研究非常迫切。传统的粉末注射成形过程的模拟研究是沿用聚合物注射成形过程的研究方法，将喂料视为基于连续介质模型的单相流和双相流，忽略颗粒的尺寸效应和粉末相的非连续性，将填充过程简化为一个相对简单的非线性动力学系统［3－6］。连续介质理论模型，对于大尺寸的粉末注射成形的工艺控制有一定的作用，但对总体轮廓尺寸小于1mm，或者虽然总体尺寸较大，但局部结构的尺寸小于1mm的注射成形制品并不适合，因为无法忽略颗粒的微尺度效应，而且也不能解释粉末和黏结剂两相分离、粉末堆积以及尺寸精度的问题。

离散单元法是一种模拟非连续介质的计算方法，在岩石力学、土力学、结构分析等领域的数值模拟中得到广泛应用，是一种新兴的非连续体分析方法。离散单元法允许单元间的相对运动，不一定满足位移连续和变形协调条件，计算速度快，所需存储空间小，特别适用于节理岩体等物质大位移，大变形分析［7－10］。离散单元法已经成为解决岩石力学问题的一种重要的数值方法，同样也能考虑用来解决离散粉末喂料的流动问题。

本工作提出对粉末注射成形的研究重点在于构建符合实际情况的离散元模型，将粉末离散相不再简化为连续相，而是处理为符合牛顿定律、具有相互作用的颗粒模型，黏结剂处理成颗粒间的黏性连接，建立粉末喂料充模过程的接触力学模型［11，12］，进行数值求解，揭示粉末注射坯的性能和喂料构成、型腔结构、注射参数之间的内在联系。

1 颗粒模型的建立

粉末喂料通常含有约60%（质量分数）的粉末颗粒，属于密集颗粒流，黏结剂在颗粒间基本形成液体桥。因此，针对粉末注射成形采用的颗粒模型中，喂料被处理成密集刚性颗粒，而黏结剂处理成颗粒间的黏性液桥连接。

假设粉末颗粒是刚性体，粉末颗粒的直接接触发生在很小范围内，接触处允许有一定重叠量。当粉末颗粒接触时相互作用力包括颗粒之间的直接接触力和液桥的黏性力。直接接触力由公式（1）～（3）决定，其法向力大小与颗粒刚度和颗粒间重叠量成正比［13，14］。而对于液桥的黏性力采用平行黏结模型近似模拟黏性液桥。平行黏结采用一组作用在接触面上具有法向和切向刚度的弹簧表示。这组弹簧，均匀分布在接触平面上，由于存在平行黏结刚度，接触颗粒的相对运动使得其中的黏结性材料产生了一个力和一个力矩，这个力和力矩作用在两个黏结颗粒上，并与黏结性材料在黏结边界上的最大法向和切向应力相关。如果最大应力超过相应的黏结强度，平行黏结就被破坏。

颗粒由于挤压而直接相互作用时，颗粒A和B之间的直接接触力为

当模拟液桥的平行黏结模型在初始状态建立后，颗粒间的黏性力初始化为零，对应着喂料在料筒内的初始状态。在注射压力作用下，颗粒间的位移增量和旋转增量引起黏性力及力矩的增量，如果最大应力及力矩超过最大黏结强度，则平行黏结破裂。每一个时间步长位移所对应的黏性力增量计算为（仅以法向力为例）

2 颗粒模型离散元微观参数的标定

离散元模型的建立，需要通过设置不同的微观参数得到宏观力学性质不同的物理模型，为使得其能够尽可能地符合真实材料的物理特性，需要通过实验确定微观参数。因此，采用蜡基黏结剂与17－4ph不锈钢粉末混料后注射得到标准拉伸样和弯曲样注射坯，利用单轴拉伸和三点弯曲的力学实验来校准微观参数，以验证微观结构模型的可靠性。实验所用设备为三思微机控制万能试验机。

注射成型实验参数如表1所示，得到的注射坯示意图如图1所示。

表1 注射成型实验参数Table 1 Parameters for injection molding test

2.1 单轴拉伸模拟及实验

首先按实际尺寸构建边界，并在边界内随机位置生成颗粒模型，采用半径扩展法使得颗粒充满型腔，然后在颗粒间赋予平行连接，并撤除边界，构建拉伸样初始状态。对试样两端施加相对作用力，模拟单轴拉伸实验，主要模拟参数如表2所示，模拟过程及结果如图2所示。

表2 主要模拟参数Table 2 Key parameters for simulation

图2 颗粒模型状态 （a）初始状态；（b）拉断状态速度矢量及黏结力；（c）完全拉断状态Fig.2 State of granular model（a）initial state；（b）speed vectors and cohesive force of abruption state；（c）completive abruption state

采用一组5个拉伸样注射坯在三思微机控制万能试验机上进行单轴拉伸实验，得到的拉断试样如图3所示。实验结果如表3所示。单轴拉伸实验和采用颗粒模型模拟得到的力－位移曲线如图4所示。

图3 单轴拉伸试样的拉断状态Fig.3 Abruption state of uniaxial tension sample

表3 拉伸实验结果Table 3 Result of tensile experiment

图4 单轴拉伸实验和模拟得到的力－位移曲线Fig.4 Force－displacement curves of uniaxial tension test and simulation

对比图2和图3，发现单轴拉伸试样裂纹形态和位置基本一致。由图4可知，单轴拉伸的实验结果与颗粒模型模拟的结果基本相符。可知，模拟的微观参数设置与喂料宏观参数相对应。

2.2 三点弯曲模拟及实验

三点弯曲模拟采用的模拟方法与拉伸实验模拟类似，模拟微观参数一致，首先按实际尺寸构建矩形边界，在边界内随机位置产生颗粒，采用半径扩展法使得颗粒填充矩形边界内部，当颗粒达到静态平衡时在颗粒间赋予平行连接，然后撤除边界。为模拟实验条件的三个压头，分别在上部和下部构建3个圆形墙体，下部两个支撑墙体保持静止，上部圆形墙体缓慢下压，颗粒模型压断过程如图5所示。

三点弯曲裂纹形貌如图6所示。表4为三点弯曲实验结果。三点弯曲实验与颗粒模型模拟得到的力－位移曲线如图7所示。

图5 颗粒模型压断过程 （a）三点弯曲初始状态；（b）三点弯曲断裂状态Fig.5 Pressing process of granular model（a）initial state of three－point bending test；（b）abruption state of three－point bending test

图6 三点弯曲裂纹形态Fig.6 Crack morphology of three－point bending test

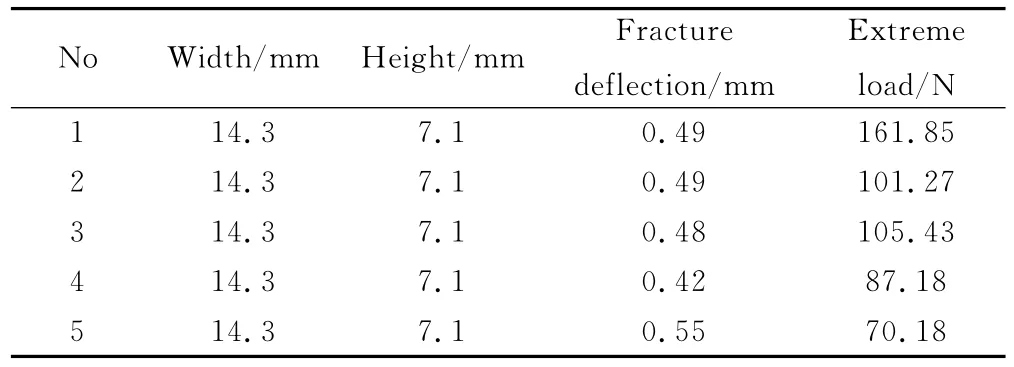
表4 三点弯曲实验结果Table 4 Results of three－point bending test

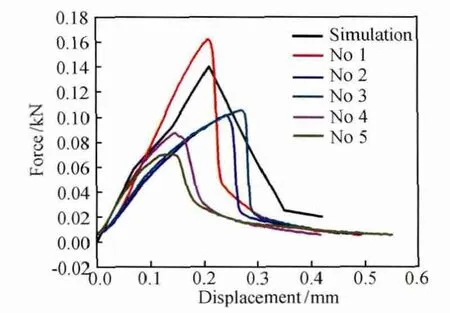
图7 三点弯曲实验和模拟得到的力－位移曲线结果Fig.7 Force－displacement curves of three－point bending test and simulation

对比图5与图6，发现在裂纹形态和位置上两者基本一致。由图7可知，实验曲线与模拟曲线基本相符。由此，可以验证颗粒模型的微观参数设置合理。

3 结论

（1）采用离散元颗粒模型可以模拟粉末喂料之间相互作用问题，其中粉末可以处理为允许有重叠量的刚性体，黏结剂处理成颗粒间的黏性连接，采用平行黏结模型近似模拟黏性液桥。

（2）通过对比粉末注射坯单轴拉伸、三点弯曲实验和离散元颗粒模型模拟的裂纹形态、位置和力－位移曲线，发现其具有一致性，这说明离散元颗粒模型的微观参数设置合理。

［1］GARINO T J，MORALES A M，BOYCE B L.The mechanical properties，dimensional tolerance and microstructural characterization of micro－molded ceramic and metal components［J］.Microsystem Technologies，2004，（10）：508－511.

［2］ANDREAS GREINER，DAVID KAUZLARIC′，KORVINK J G，et al.Simulation of micro powder injection moulding：powder segregation and yield stress effects during form filling［J］.Journal of the European Ceramic Society，2011，31（14）：2525－2534.

［3］XIAO F，IKEBATA A.An efficient method for capturing free boundaries in multi－fluid simulations［J］.International Journal for Numerical Methods in Fluids，2003，42（2）：187－210.

［4］LI C T，ISAYEV A I.Interface development and encapsulation in simultaneous co－injection molding of disk（I）：two－dimensional modeling and formulation［J］.Journal of Applied Polymer Science，2003，88：2300－2309.

［5］LI C T，LEE D J，ISAYEV A I.Interface development and encapsulation in simultaneous co－injection molding of disk（II）：two－dimensional simulation and experiment［J］.Journal of Applied Polymer Science，2003，88：2310－2318.

［6］TAN KH，YUEN MMF.A fuzzy multiobjective approach for minimization of injection molding defects［J］.Polymer Engineering and Science，2000，40（4）：956－971.

［7］SOLLIE WEH，BOKHOVE O，VAN DER VEGT JJW.Spacetime discontinuous Galerkin finite element method for two－fluid flows［J］.Journal of Computational Physics，2011，230（3）：789－817.

［8］母福生，杨鹏.搅拌磨机介质运动离散元数值模拟分析［J］.中国机械工程，2012，23（20）：2465－2468.MU Fu－sheng，YANG Peng.Analysis of DEM numerical simulation of media movement for a stirred mill［J］.China Mechanical Engineering，2012，23（20）：2465－2468.

［9］ORIANNE J，DANIEL D，RICHARD K.Discrete element modeling of a granular platform supported by piles in soft soil－validation on a small scale model test and comparison to a numerical analysis in a continuum［J］.Computers and Geotechnics，2009，36（6）：917－927.

［10］CUMMINS SJ，CLEARY P W.Using distributed contacts in DEM［J］.Applied Mathematical Modeling，2011，35（4）：1904－1914.

［11］刘煜，李益民，夏卿坤，等.基于颗粒模型的取样钳粉末注射成形［J］.中南大学学报，2012，43（10）：3847－3851.LIU Yu，LI Yi－min，XIA Qing－kun，et al.The research on powder injection molding of sampling clamp based on granular model［J］.Journal of Central South University，2012，43（10）：3847－3851.

［12］刘煜，李益民，夏卿坤，等.基于颗粒模型的二维矩形模腔粉末微注射成型研究［J］.材料工程，2010，（5）：5－9.LIU Yu，LI Yi－min，XIA Qing－kun，et al.Micro powder injection molding in two－dimensional rectangular cavity based on granular model［J］.Journal of Materials Engineering，2010，（5）：5－9.

［13］PROCHAZKA P P.Application of discrete element methods to fracture mechanics of rock bursts［J］.Engineering Fracture Mechanics，2004，71（4－6）：601－618.

［14］TAMAGNINI C，CALVETTI F，VIGGIANI G.An assessment of plasticity theories for modeling the incrementally nonlinear behavior of granular soils［J］.Journal of Engineering Mathemat－ics，2005，52（1－3）：265－291.