解析第二重要极限的三步骤法

华婷,文传军

(常州工学院理学院，江苏常州213002)

第二重要极限是“高等数学”课程中极限部分的一个重要内容[1-2]，是处理1∞未定型极限的有效方法。由于第二重要极限存在2种基本表达形式，且应用时需要构造特定的极限形式，学生对于该公式的学习、掌握及灵活应用存在一定困难。

对于第二重要极限的研究，主要分为两方面：一是第二重要极限公式的证明研究，大多集中在公式数列形式单调性的证明。包括利用数列展开证明单调性，以及利用算数平均大于几何平均进行单调性证明；二是第二重要极限公式应用技巧方面的研究。夏桂梅[3]通过对第二重要极限表现形式及特性的研究分析，得出了它的一些推广定理，并给予证明，同时得到了一些容易掌握的应用技巧；高建云[4]从实际应用出发逐步过渡到知识的讲解,阐述了无穷数e与第二重要极限的关系，期望有助于学生学习动机的激发和知识迁移能力的提高；张正宇[5]分析了极限问题转换为第二重要极限形式所需要满足的基本要素；文献[6]联合应用第二重要极限和罗比达法则求1∞的幂指函数极限，使幂指函数极限求值问题变得既方便又简单。文献[6]通过2个结论实现，其中结论2给出的条件与结论并不严谨，且结论2中最终结果的表示需中间变量转换，增加了掌握和学习难度。

在上述研究工作的基础上，提出了解析第二重要极限的三步骤法，利用幂指函数连续性计算极限，并将计算步骤细分为一判定、二构造“1加”形式、三构造指数倒数形式，从而降低了对该公式学习和应用的难度。

1 三步骤法

1.1 学习第二重要极限存在的问题

第二重要极限公式为

(1)

由式(1)可知，第二重要极限公式存在2种基本极限形式：一是自变量x趋近于0时；二是自变量x趋近于无穷时。如果再考虑左右极限等情况，式(1)可衍生出许多种极限形式。

仅就2种最基本的极限形式而言，为了掌握第二重要极限，学生需要记忆不同的计算公式，增加了学生学习和记忆的负担；同时这2种极限形式非常相似，学生们学习时总是容易将二者混淆起来，包括对自变量趋近的混淆以及函数形式的混淆，进而导致了极限计算的最终错误。另外，在构造底函数“1加”形式时，一般要求结合具体题目采用不同途径构造，增加了解题过程的变化形式，进一步加大了该知识点学习和应用的困难。因此，第二重要极限公式的应用或者1∞未定型极限是极限计算部分的难点。

1.2 三步骤法

为了能够让第二重要极限公式变得简单易懂，帮助学生牢固而有效地掌握该公式的核心并灵活应用之，对第二重要极限公式进行了研究分析，将其解析过程归纳分解为3个基本步骤，并称之为第二重要极限的三步骤法，具体如下说明。

幂指函数的极限形式为

limf(x)g(x)

(2)

步骤1 利用无穷大与无穷小的关系等方法，判定极限式(2)的类型为1∞未定型极限。

步骤2 构造底函数“1加”的形式，即令

f(x)=[1+(f(x)-1)]

(3)

其中：f(x)>0,f(x)≠1。

此处需要特别说明的是，有许多教学或辅导教材要求同学们根据具体题目去构造函数“1加”的形式，但正是因为不同的题目有着各种不同的构造途径，导致学生无法正确理解并有效掌握这些繁琐的变换途径，对于不同的题目而感到无所适从。为了帮助学生对于任何1∞未定型极限都能够准确处理，在三步骤法的第二个步骤中，统一要求学生通过“加1减1”的方法来构造“1加”底函数形式，其形式如式(3)所示。

步骤3 构造指数函数倒数形式，即令

(4)

由此，则有

limf(x)g(x)=lim [1+(f(x)-1)]g(x)=

(5)

由第二重要极限及limf(x)g(x)为1∞未定型极限可知

(6)

设lim (f(x)-1)g(x)=a，结合式(5)、式(6)，从而有

limf(x)g(x)=ea

(7)

通过第二重要极限的三步骤法可知，整个极限过程除了极限lim (f(x)-1)g(x)需特定计算外，其他部分几乎与试题具体函数内容毫无关系，学生在掌握该方法时几乎不需要根据具体试题而采用不同变化形式和方法，从而降低掌握及应用该知识点的难度。而极限lim (f(x)-1)g(x)也可结合等价无穷小、洛必达法则等方法计算得到。

下面利用一算例来说明该方法的应用情况。

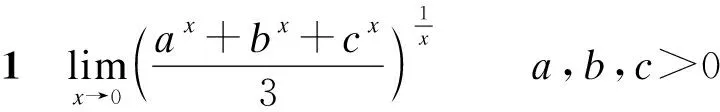
解析：

①判断类型。

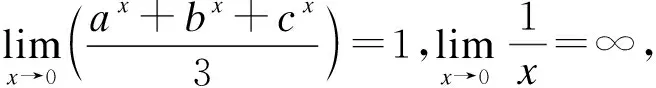
②构造“1加”形式，即

③构造指数倒数形式，即

这里可以考虑使用等价无穷小计算，当x→0时，ax-1～xlna，则

ax+bx+cx-3=(ax-1)+(bx-1)+(cx-1)～x(lna+lnb+lnc)

此处要求lna+lnb+lnc≠0，则

所以有

1.3 三步骤法的理论依据

文献[7]中利用复合函数连续性及极限运算法则，得到如下结论。

对形如f(x)g(x)的幂指函数(f(x)>0,f(x)≠1)，若limf(x)=a>0，limg(x)=b，则

limf(x)g(x)=ab

(8)

结合三步骤法，有

limf(x)g(x)(1∞)=

lim(f(x)-1)g(x)=a

则

limf(x)g(x)=ea

上述分析推导中，其核心在于极限lim (f(x)-1)g(x)是存在的，而实际上此极限还存在为∞的情况，当(f(x)-1)g(x)趋向为-∞或+∞时，整个幂指函数的极限将会发生改变，最终结果可以归纳为式(9)。

limf(x)g(x)(1∞)=

(9)

虽然有上述3种情况，但在实际教学及考试中，学生所接触到的，仅有极限lim (f(x)-1)g(x)=a的情况，所以同学们只需掌握该种情况下的计算步骤及结果即可。

2 考研数学中三步骤法的应用

正是因为第二重要极限的复杂性和应用计算时难度较大，所以在研究生升学考试数学试题中该知识点也频繁出现。熟练掌握第二重要极限三步骤法，可以帮助同学们快速、有效、简便地计算考研数学试题中的1∞未定型极限。

②构造“1加”形式，原式等于

③构造指数倒数形式

所以原式等于ea+b。

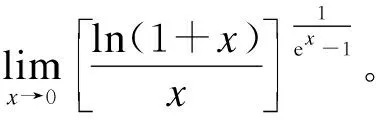
且有

所以有

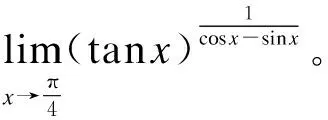
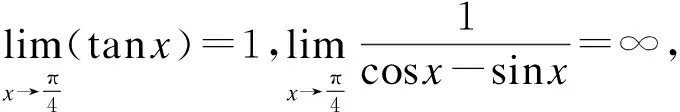
则

通过上述3个典型考研例题及解答过程可知：①1∞类型的极限是历年考研试题中频繁出现的试题，从而体现了该知识点的重要性和掌握应用的难度；②学生即使没有记住第二重要极限公式的2种基本形式，或者对应用该公式存在混淆不清的情况，只要按照三步骤法的3个基本步骤固化操作，结合等价无穷小、洛必达法则等也可以达到求解计算极限的目的。

3 结语

本文提出了解析第二重要极限的三步骤法，将第二重要极限公式的应用细分为3个基本步骤，即判定、构造“1加”形式和构造指数倒数形式，降低了第二重要极限公式学习和应用的难度，使得学生对1∞类型的极限可以有效地进行解析，同时提高了公式的简易实用性。