基于最大能量匹配与样本熵的小波降噪方法

常天庆，李勇，陈军伟，张洋

装甲兵工程学院控制工程系，北京 100072

基于最大能量匹配与样本熵的小波降噪方法

常天庆，李勇，陈军伟，张洋

装甲兵工程学院控制工程系，北京 100072

为提高自适应小波阈值降噪方法的效果，提出一种结合最大能量匹配的小波包分解和快速样本熵的小波阈值降噪方法。根据各层小波系数特点并以最大能量匹配准则自适应选择小波包基对含噪信号进行分解，对最大尺度下的小波系数阈值化后重构得到噪声信号，采用快速样本熵算法计算噪声信号样本熵，动态调整阈值使噪声信号样本熵最大而获得最佳的降噪效果。应用实例表明：该方法相比传统的小波阈值降噪方法具有更好的降噪效果。

最大能量匹配准则；快速样本熵；小波阈值降噪

小波降噪方法主要有模极大值法和阈值法两类，前者实现过程比较复杂，重构信号误差较大，后者算法简捷，在信号去噪中应用较多。阈值法通常是按照一定的准则将信号各尺度下的分解信号进行阈值化处理以减少噪声分量成分。目前阈值的选择可以分为全局阈值和局部阈值两类。全局阈值对各层所有的小波系数或同一层内各节点的小波系数都采用统一的阈值，而局部阈值则是根据各层分解系数的实际情况来确定的，不同分解层中的阈值也不一样，局部阈值精度高，降噪效果好。侯建华[1]等在贝叶斯最大后验概率准则下推导出了局部自适应的MapShrink阈值，并提出了相应的降噪算法；林杰[2]等人将去噪图像的峰值信噪比作为性能指标，采用中点法进行寻优，自适应调整阈值参数；赵立业[3]等采用自适应小波阈值滤波算法对硅微陀螺输出信号进行滤波处理，很好地抑制了随机漂移；刘文艺[4]等选取最大类间方差和最小类内方差的阈值作为最佳阈值并通过改进阈值量化公式实现自适应降噪。从相关文献可以看出，目前研究较多的主要还是根据信号在各尺度中的系数特点[5-8]，自适应地选择阈值进行阈值化处理，但对于阈值的选择仍存在一定的盲目性。

本文以含噪信号中噪声的样本熵作为阈值选择标准自适应调整小波阈值。首先按照最大能量匹配准则选择最优小波包基对含噪信号进行小波包分解，然后对各尺度下的系数进行阈值处理，采用快速样本熵算法计算噪声的样本熵，以噪声样本熵最大化作为阈值选择的依据，以此达到降噪的目的。

1 最大能量匹配的小波包分解

小波变换[9]的本质是比较被分析信号与小波信号的局部相似程度。通常，在进行小波变换时，均是选择一个与被分析信号最接近的小波基在各尺度空间进行分解。但各尺度空间的近似信号随着尺度的增加会发生变化，因此单一的小波基对某些尺度空间的近似信号来说可能不再是最优小波基。因此，通常是通过不断比较各个尺度空间中近似信号与小波库中所有小波基的相似性，选择相似系数最大的小波基作为最优小波基。但这种方法比较耗时，而且当存在噪声时，通过比较信号与小波基的相似性难度比较大。

由于信号各分解系数的平方与相应的能量成正比，根据巴什瓦尔定理[10]可知，小波包分解后系数的平方具有能量的量纲，因此，小波包分解得到的系数反映了信号的能量分布。根据小波变换的这一特征，本文提出一种基于最大能量匹配准则的小波包分解算法，在对信号进行逐层小波分解时，以每层尺度空间中近似信号的能量为度量准则，选择使能量最大的小波基作为最优小波基。

基于最大能量匹配准则的小波包分解算法流程描述如图1所示。

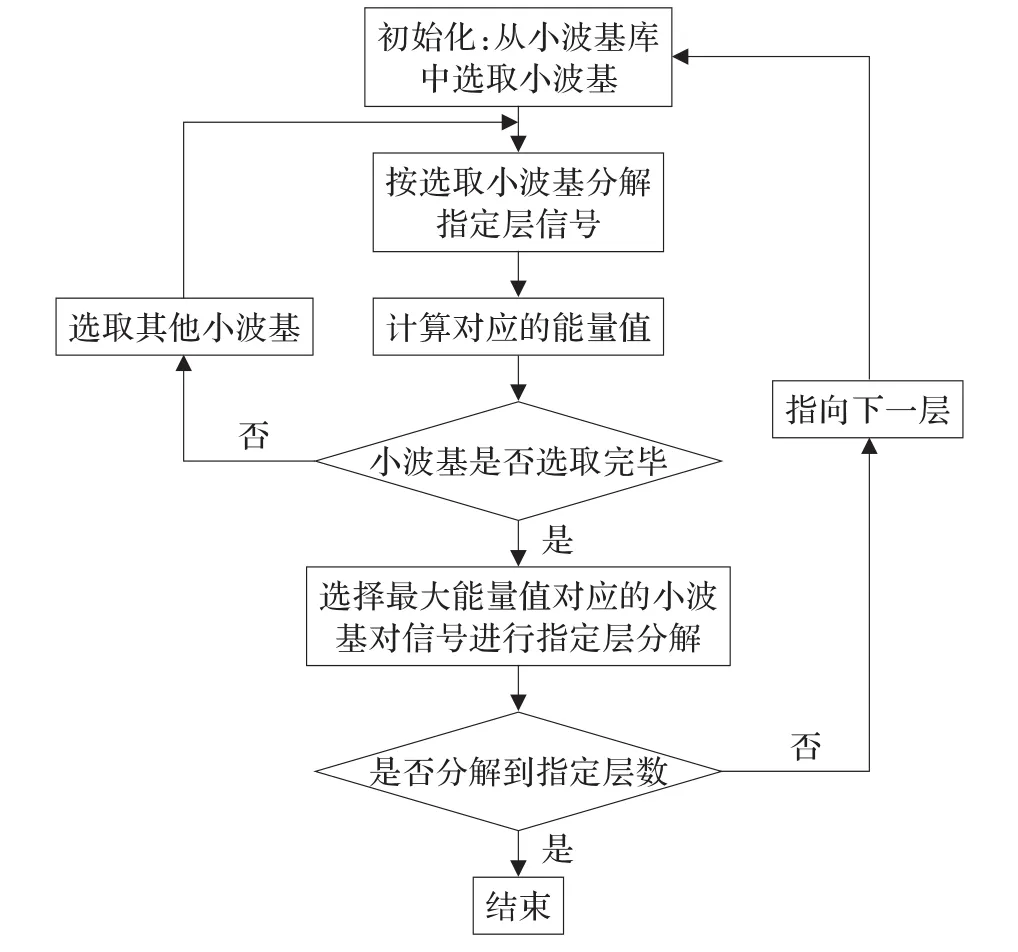
图1 最大能量匹配的小波包分解算法

具体算法描述如下：

步骤5重复步骤1至步骤4，直到分解到第l层，其对应的最优小波基分解尺度系数为SCop，l。

步骤6根据得出的各尺度空间的最优小波基，对信号进行相应尺度的分解。

2 快速样本熵算法

样本熵[11-12]是一种新的时间序列复杂性测度方法，它是在近似熵的基础上发展而来的，是对近似熵的一种修正。由确定性成分和随机成分组成的混合信号的样本熵的计算不依赖于数据的长度，只需较短的数据即可得出稳健的估计值，具有较好的抗干扰能力。当信号成分越复杂时，其样本熵越大，信号的自我相似性则越低；相反，当信号成分越单一时，其样本熵越小，信号的自我相似性就越高。本文采用样本熵来表征噪声序列的复杂程度，并作为评价去噪效果的依据。

设信号序列{s(i)}为：s(1)，s(2)，…，s(N)，其样本熵的计算过程描述如下[13]。

步骤1给定维数m，由信号序列组成m维矢量：

步骤4增加维数到m+1，按步骤1至步骤3得到Rm+1(r)。

步骤5理论上，由步骤1至步骤4可以得到样本熵：

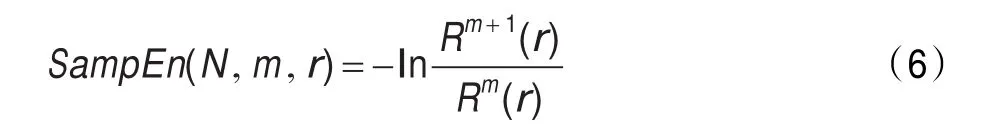
而实际应用中，一般N取有限值，则序列长度为N的信号样本熵估计值为：样本熵的值与m、r取值有关，根据经验，通常取m=2，r=(0.1～0.25)SD(u)，其中SD(u)表示信号序列的标准差。

根据步骤2和步骤3，矢量距离可以转化为：对于i、j，只要存在|s(i+k)-s(j+k)|＜r，k=0，1，…，m-1;i≠j，即能满足d(i，j)＜r，因此本文在样本熵计算方法基础上给出了一种快速算法，通过比较信号序列中序列点之间的距离与相似容限的大小，将其转化为二值变量，然后经过二进制运算，将矢量距离也转化为二值变量，这样即可把实数运算转化为逻辑“与”运算和逻辑求和运算，能显著提高计算速度。

对于长度为N的信号序列{s(i)}，定义N×N的二值绝对值矩阵为CN×N，CN×N中的第i行第j列的元素记作cij：

3 小波阈值降噪

本文在文献[14]的基础上提出一种结合最大能量匹配的小波包分解及快速样本熵的小波阈值降噪方法。

其思路是：依据最大能量匹配准则选择最优小波包基对含噪信号进行小波包分解，对最大尺度下的小波系数阈值化后重构信号，与原序列相减得到噪声序列；采用快速样本熵算法计算噪声序列的样本熵；噪声信号成分越复杂时，其样本熵越大，以此为依据来调整阈值大小，取使样本熵值最大的阈值作为最优阈值，采用最优阈值对含噪信号进行阈值化处理，重构后得到降噪后的信号。

具体实现步骤描述如下。

步骤1依据最大能量匹配准则选择最优小波包基对含噪信号进行分解，得到各个尺度下的小波系数。

步骤2采用软阈值方法对N层的小波系数进行阈值化处理，得到降噪后的小波系数。

步骤3重构阈值化后的小波系数，得到降噪信号序列。

步骤4计算降噪序列和原序列之间的差值得到噪声序列，并采用快速样本熵算法计算噪声序列的样本熵值。

步骤5逐步调整小波系数的阈值，执行步骤1～步骤4反复迭代，计算各阈值下的样本熵值。以样本熵最大作为停止的条件，此时得到的即为最优阈值。

步骤6采用最优阈值对含噪信号进行阈值化处理，重构后得到降噪后的信号。

随着阈值的增加，噪声序列越来越复杂，其样本熵会逐步增加。当去噪效果最佳时，得到的噪声序列最复杂，样本熵达到最大。此后，部分有用信号也被消除，导致噪声被有用信号淹没，噪声序列的样本熵将会减小。因此，噪声的样本熵值呈现出先增加后减小的变化过程[14]。

4 应用实例

在对设备进行在线故障诊断时，通常采集重要的运行信号进行分析，而由于设备运行环境十分恶劣，常常导致采集到的信号受强噪声干扰，因此需要对含噪信号进行降噪处理。本章以坦克炮控系统故障诊断时所需要的电机起动直至稳态运行过程中的电枢电流信号降噪为例，验证本文提出方法的有效性及优越性。

采用以下三种方法对电机电枢电流信号进行降噪实验：

方法1采用常规的基于单一基小波分解以及软阈值的去噪方法进行降噪。

方法2采用文献[14]描述的基于单一小波基与样本熵的自适应小波消噪算法进行降噪。

方法3采用本文提出的小波阈值降噪算法进行降噪。

为了定量比较不同降噪方法的效果，定义了几个度量信号降噪效果的指标参数[15]，即均方误差MSE、信噪比SNR和相对幅值误差ME。三个指标参数的定义如下：

式（12）～（14）中，x1为含噪声的信号，x2为降噪后信号，N为信号长度。MSE表征两个信号的相似性，SNR表征降噪效果，ME表征降噪后信号相对于原始信号的相对幅值误差。

图2～图5给出了不同降噪方法下的电机电枢电流信号降噪效果对比图。直观上看，方法3比方法1和方法2具有更好的降噪能力，能够滤除大部分噪声信号，且对原始信号的畸变最小。

图2 含噪信号

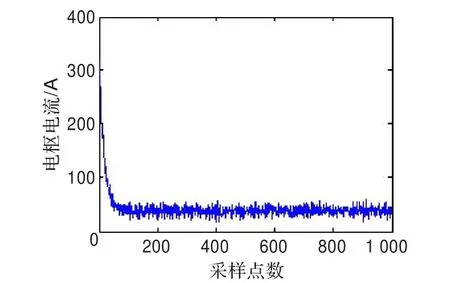
图3 采用方法1降噪后的信号

图4 采用方法2降噪后的信号

图5 采用方法3降噪后的信号

表1给出了不同方法下，电枢电流信号降噪后的MSE、SNR和ME。从表中可以看出，采用方法3降噪后信号的MSE和ME都最小，这说明采用最优小波基分解比采用单一小波基分解的降噪效果要好。而方法3的信噪比最大主要是因为该方法能根据各层信号特征自适应地选择小波包基进行分解，另外，采用样本熵能够较好地描述噪声信号的特征，能够最大程度地分离出噪声信号，更有利于信、噪的分离。

表1 不同降噪方法的性能比较

在相同硬件配置下，采用Matlab对1 000个采样点的电枢电流信号进行降噪处理，三种方法所需要的运算时间见表1。方法1采用单一小波单一阈值进行降噪，计算量最小，所用时间也最少；方法3相比方法2增加了最优小波包基选择的运算量，因此总时间要长，但采用了快速样本熵算法，导致两种方法的运算时间却相差不是很大。

5 结束语

本文提出一种结合最大能量匹配准则的小波包分解和快速样本熵算法的信号降噪方法。该方法首先对含噪信号进行多尺度下的最优小波包基分解，然后采用快速样本熵算法计算噪声信号的样本熵，以噪声信号样本熵作为降噪效果评价指标，通过调整阈值使噪声样本熵最大从而获得最佳降噪效果。应用实例表明，本文方法比常规小波阈值方法以及基于单一小波基和样本熵的自适应消噪方法效果都要好，能减小对原始信号的畸变，具有更好的降噪性能。

[1]侯建华，田金文.基于贝叶斯最大后验估计的局部自适应小波去噪[J].计算机工程，2006，32（11）：13-15.

[2]林杰，付梦印，李道平.自适应小波阈值去噪算法及在图像处理中的应用[J].兵工学报，2011，32（7）：896-900.

[3]赵立业，王寿荣.基于自适应小波阈值的硅微陀螺信号处理方法[J].微计算机信息，2009，25（12）：4-6.

[4]刘文艺，汤宝平，蒋永华.一种自适应小波消噪方法[J].振动、测试与诊断，2011，31（1）：74-77.

[5]刘杨，金天.小波降噪在微弱GPS信号捕获中的应用[J].系统工程与电子技术，2011，33（4）：842-846.

[6]王国栋，胡邦喜，高立新，等.自适应小波降噪在轴承故障诊断中的应用[J].噪声与振动控制，2007（5）：100-103.

[7]何存富，刘溯，刘增华，等.小波降噪在钢绞线缺陷检测中的应用[J].机械工程学报，2008，44（7）：118-122.

[8]王传鑫，邵诚，韩瑜.基于蚁群算法的小波降噪双阈值优选方法[J].控制与决策，2011，26（1）：115-119.

[9]Burrus C S.小波与小波变换导论[M].程正当，译.北京：机械工业出版社，2007.

[10]徐守时.信号与系统理论、方法及其应用[M].合肥：中国科学技术大学出版社，2006.

[11]王新沛，杨静，李远洋，等.基于样本熵快速算法的心音信号动力学分析[J].振动与冲击，2010，29（11）：115-118.

[12]张涛，任志良，孙常存，等.基于小波包分解和样本熵的电磁干扰分析方法[J].海军工程大学学报，2011，23（5）：82-87.

[13]苏文胜，王奉涛，朱泓，等.基于小波包样本熵的滚动轴承故障特征提取[J].振动、测试与诊断，2011，31（2）：162-166.

[14]尚晓三，王式成，王振龙，等.基于样本熵理论的自适应小波消噪分析方法[J].水科学进展，2011，22（3）：182-188.

[15]金卓睿.变压器局部放电超高频监测分形天线与最优小波去噪及信号识别研究[D].重庆：重庆大学，2008.

CHANG Tianqing,LI Yong,CHEN Junwei,ZHANG Yang

Department of Control Engineering,Academy of Armored Forces Engineering,Beijing 100072,China

In order to enhance effect of adaptive wavelet threshold de-noising method,a new wavelet threshold de-noising method combining wavelet packet decomposing based on maximum energy matching and fast sample entropy is presented. According to feature of each layer wavelet coefficient,wavelet packet base is selected adaptively based on maximum energy matching criterion to decompose signal with noises and then the wavelet coefficient under maximum scale is processed with threshold and is restructured to get noise signal.Fast sample entropy algorithm is used to compute sample entropy of noise and the threshold is adjusted dynamically to make sample entropy of noise maximum and obtain optimal de-noising effect.The results by example show that the method presented in this paper has better de-noising effect compared with traditional wavelet threshold de-noising.

maximum energy matching criterion;fast sample entropy;wavelet threshold de-noising

A

TP301.6

10.3778/j.issn.1002-8331.1212-0348

CHANG Tianqing,LI Yong,CHEN Junwei,et al.Wavelet threshold de-noising method based on maximum energy matching and fast sample entropy.Computer Engineering and Applications,2014,50（21）：210-213.

常天庆（1963—），男，教授，博士生导师，主要研究方向为装备自动化系统检测与故障诊断；李勇（1983—），男，博士研究生，主要研究方向为装备智能故障诊断、预测与健康管理。E-mail：liyong169@aliyun.com

2012-12-29

2013-03-13

1002-8331（2014）21-0210-04

CNKI出版日期：2013-10-29，http://www.cnki.net/kcms/detail/11.2127.TP.20131029.1133.024.html