基于改进谱聚类的图像分割算法
关昕,周积林
1.辽宁工程技术大学电子与信息工程学院,辽宁葫芦岛 125105
2.辽宁工程技术大学研究生学院,辽宁葫芦岛 125105
基于改进谱聚类的图像分割算法
关昕1,周积林2
1.辽宁工程技术大学电子与信息工程学院,辽宁葫芦岛 125105
2.辽宁工程技术大学研究生学院,辽宁葫芦岛 125105
针对传统谱聚类算法应用于图像分割时仅采用特征相似性信息构造相似性矩阵,而忽略了像素分布的空间临近信息的缺陷,提出一种新的相似性度量公式——加权欧氏距离的高斯核函数,充分利用图像特征相似性信息和空间临近信息构造相似性矩阵。在谱映射过程中,采用Nystrom逼近策略近似估计相似性矩阵及其特征向量,大大减少了求解相似性矩阵的运算复杂度,降低了内存消耗。对得到的低维向量子空间采用一种新型的聚类算法——近邻传播聚类算法进行聚类,避免了传统谱聚类采用K-means算法对初始值敏感,易陷入局部最优的缺陷。实验表明该算法获得了比传统谱聚类算法更好的分割效果。
谱聚类;空间临近信息;相似性矩阵;Nystrom逼近策略;近邻传播聚类算法
1 引言
在计算机视觉理论中,图像分割与特征提取,目标识别构成了计算机视觉领域从低到高的三个层次,特征提取与目标识别都以图像分割为基础,分割的好坏直接影响到后续特征提取和目标识别的质量[1]。由于图像的复杂多变性,目前还没有一种算法能够通用于所有的图像,都是针对具体问题采用具体的算法[2]。因此,图像分割算法的研究越来越受到人们的重视。传统的图像分割方法可以分为三类:基于区域的分割、基于边界的分割和基于纹理的分割。近几十年来,随着一些新理论和新方法的提出和应用,图像分割方法层出不穷,其中比较有代表性的是基于聚类、遗传算法、神经网络、支持向量机、水平集和数学形态学的分割方法。近年来,基于图论的谱聚类算法由于其良好的特性,已得到越来越多的关注,成为一个新的研究热点。
谱聚类是基于谱图划分理论[3-6]的一种新型的聚类算法,它是一种点对聚类算法,其本质是将聚类问题转化为图的最优划分问题。该算法能在任意形状的样本空间进行聚类,能快速收敛到全局最优解,避免了传统的聚类如K-means算法只能在凸球形样本空间进行聚类而在非凸球形样本空间容易陷入局部最优解的缺点。具有识别非高斯分布的能力,较其他聚类算法具有明显的优势,目前已经广泛应用于文本挖掘、网页划分、语音识别、VLSI设计等领域。谱聚类应用于图像分割,通常能取得很好的分割效果,但同时它也有着自身的缺陷——相似性矩阵构造的局限性,存储和计算相似性矩阵的高复杂度,以及子空间聚类不稳定。文献[7]中提出基于路径的相似性度量,但对边界点过于敏感,效果不理想;文献[8]提出基于密度敏感的相似性度量,但当位于高密度区的两个样本数据点穿过的路径很长时,效果不明显,并且最终采用K-means聚类简化后的向量空间,造成聚类结果不稳定。本文以谱聚类算法为基础,考虑上述缺陷,通过三方面对谱聚类进行了改进,并应用于图像分割。
2 谱聚类算法
谱聚类算法将图像看成是一种基于某种相似性的无向加权图G=(V,E),其中V代表一个数据样本在无向加权图中的顶点,E为顶点间的边,基于某种相似性对其赋予权值w。由于相似性矩阵包含了图像所有的数据结构信息,基于某种划分准则来进行聚类划分,使得划分的子类之间具有较高的相似性,不同子类之间具有较低的相似性。一般的,划分准则可分为二路划分准则和多路划分准则。文献[9]中简单介绍了常见的二路划分准则有最小划分准则(Minimum cut),规范割集准则(Normalized cut),比例割集准则(Ratio cut),平均割集准则(Average cut),最大最小划分准则(Min-max cut)。基于二路划分准则的谱聚类算法一般通过迭代对样本数据进行聚类。文献[5]通过研究证明,使用更多的特征向量,直接计算多路分割将会得到更好的分割效果。其中比较经典的是由Meila和Shi提出的MS算法[10]以及Ng等人提出的NJW算法[11]。本文便是采用多路规范割集准则[12](Multi way Normalized cut)对图像进行分割。由于不同准则函数的选取和不同的谱映射方法,谱聚类算法又有着不同的实现方法,但基本框架都是一致的,以NJW算法为例,其步骤如下:
(1)根据样本间的某种相似性构造相似性矩阵W,传统谱聚类一般都是基于欧氏距离的高斯核函数来度量样本数据点之间的相似性,构造相似性矩阵W,图像像素信息为X=(x1,x2,…,xn),数据间的相似性如下式:
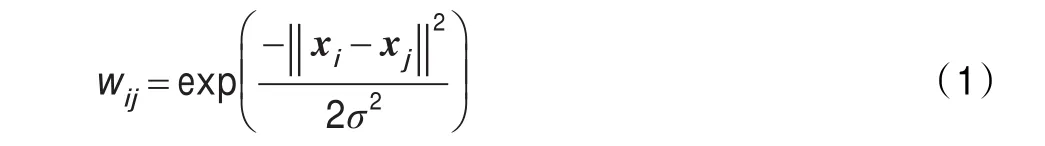
其中σ为尺度参数。
(2)构造拉普拉斯矩阵L=D-1/2WD-1/2,其中D是对角矩阵,对角元素为d:

计算拉普拉斯矩阵L的前k个最大特征向量xi,构造一个低维向量子空间X:

(3)将矩阵X的行向量转化成单位向量构造矩阵Y。

(4)将矩阵Y中的每一行看作是子空间中的一个点,对其应用K均值聚类进行划分。
(5)如果矩阵Y第y行被划分到第j类,则对应的像素点也被划分到第j类。
3 改进的谱聚类算法
由于谱聚类能在任意样本空间进行聚类并能很好地收敛到全局最优解,目前已广泛应用于图像分割领域。伴随着这些优点的同时,谱聚类的缺陷也制约着它的发展。本文根据传统谱聚类的缺陷,提出了三点改进,弥补了传统谱聚类的不足,经实验验证,得到了比传统谱聚类更好的分割效果。
3.1 加权欧氏距离构建相似性矩阵
传统谱聚类利用高斯核函数来构建样本数据点之间的相似性,具体构建方法见第2章步骤(1),公式(1)仅仅考虑了图像的特征相似性信息,用像素值之间欧式距离的大小来度量相似性,距离越大相似性越小,距离越小相似性越大,忽略了样本数据点之间的空间邻近信息,并且可能会夸大某些较大像素值的作用。由于空间邻近信息和图像像素值信息具有不同的量纲,对于不同性质的指标直接相加不能正确反映不同作用的综合结果,而直接相乘无疑是加大了计算的复杂度,如文献[13]提出的同时兼顾空间邻近信息和图像特征相似性信息的相似性度量公式:
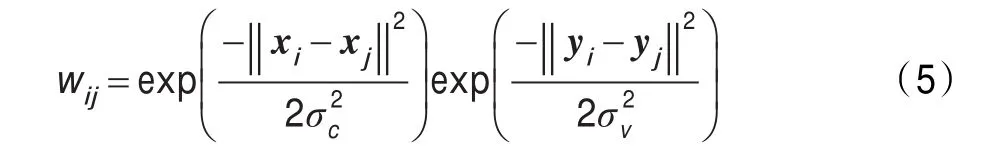
X=(x1,x2,…,xn)为图像像素值信息,Y=(y1,y2,…,yn)代表样本的空间位置信息。该公式引入了一个新的尺度参数σv,不仅增加了算法对初始参数的敏感性,而且计算机计算一次指数运算所运用的时间是乘积运算的30倍多,运算时间消耗巨大。为了能同时利用样本像素信息和空间邻近信息,本文定义加权欧氏距离的相似性度量函数为:
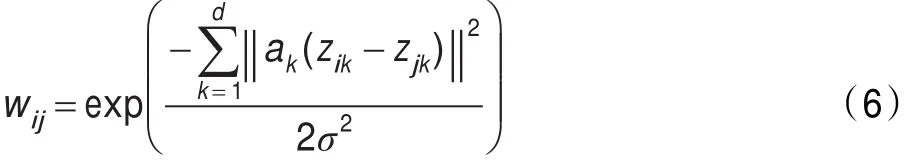
其中ak为权重,d维向量z表征每一个样本点的信息,假设有n个样本点:z1=(z11,z12,…,z1d),z2=(z21,z22,…,z2d),…,zn=(zn1,zn2,…,znd),向量中包括其像素值信息和空间位置信息。如何构造这个权重才能达到理想的效果,本文考虑到同时消除量纲和变量自身较大值所起作用的影响,对所有样本数据点相同维数的同属性分量进行标准化,即对z11,z21,…,zn1标准化得到其平均值e1和方差s1,对z12,z22,…,zn2标准化得到其平均值e2和方差s2,依照同样方法,共得到d个平均值ek(k=1,2,…,d)和d个方差sk(k=1,2,…,d),定义相似性矩阵度量公式为:
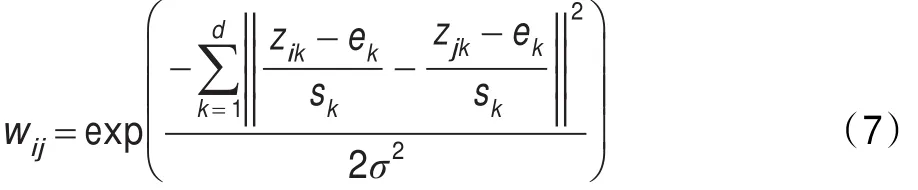
其中zik表示第i个样本点第k维属性,简化可得:
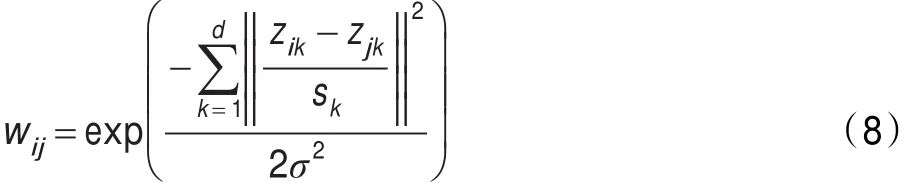
σ为尺度参数,将方差的倒数看作是一个权重,便得到本文所定义的一个加权欧氏距离的相似性度量公式。
3.2 Nystrom逼近策略
由于图像数据的复杂庞大性,计算和存储相似性矩阵给计算机运算带来了极大的困扰。对于一个有n个像素点的图像来说,其相似性矩阵异常庞大,空间复杂度是O(n2),并且计算相似性矩阵的特征向量又进一步增加了运算量,根据文献[14],引入了Nystrom逼近策略来间接求解相似性矩阵的特征向量,降低谱聚类算法的计算复杂度和计算机内存消耗。
其基本思想是用随机采样的方式获得一定的采样点,用采样点与未采样点之间的相似性来近似估计未采样点之间的相似性。当采样点的规模能足以反应图像内在特征时,随机采样随机性的负面影响便可得到有效的抑制,此时算法稳定并且能取得较好的效果。本文随机选取图像像素点的1%作为采样点。当采样点低于1%时,不能很好地代表图像的内在特征,图像最后的分割效果一般;当采样点高于1%时,能取得更好的分割效果,但空间和时间复杂度的增加相对于分割效果的增加来说,显得有点得不偿失。

设原始图像像素个数为n,从原始图像中随机采样m个像素点(m≪n),则相似性矩阵W可分解为:其中A是用公式(8)计算的m个采样点之间的相似性矩阵,B是m个采样点与剩下的(n-m)个像素点之间的相似性矩阵。C代表剩余的(n-m)个像素点之间的相似性矩阵,由于剩余像素点数非常繁多,计算矩阵C的运算量相当大。现将矩阵A对角化得A=UΛUT,利用矩阵A和矩阵B来近似逼近相似性矩阵W和其特征向量:

为了使Nystrom逼近策略能够用于求解基于多路规范割集准则的相似性矩阵,受文献[15]启发,先采用Nystrom逼近策略计算相似性矩阵A和B,利用矩阵A和矩阵B计算W每行元素的和:

其中I为一个单位列矩阵。采用如下公式逼近D-1/2WD-1/2的值:
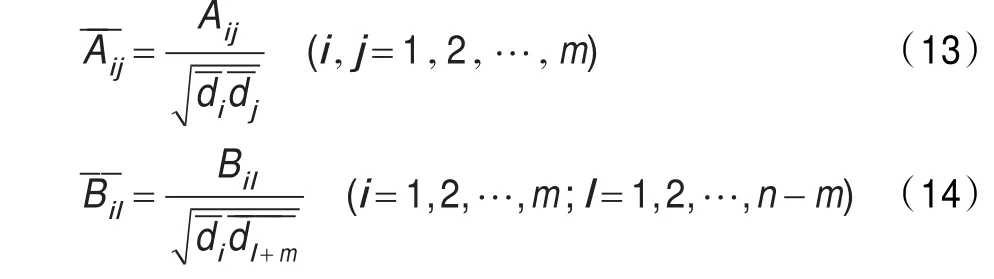

3.3 近邻传播聚类算法(Affinity Propagation)
传统谱聚类算法利用相似性矩阵的特征向量构造一个低维向量子空间,这个子空间结构更加明显。将这个子空间,也就是第2章步骤(4)得到的矩阵Y的每一行看成是一个样本点,一般利用K-means算法对这个子空间进行聚类。由于K-means算法事先不能确定聚类数目,需要人为初始化,对初始值敏感,不同的初始值可能会得到不同的聚类效果,且容易陷入局部最优,分割效果不稳定。针对这些问题,本文使用了一种快速高效的新型聚类算法——AP算法[16]。它是Frey和Dueck于2007年提出的一种新的聚类算法,以样本之间的相似性矩阵为输入,输出的是聚类中心和样本与聚类中心的所属度关系,能够很好地解决非欧空间和大规模稀疏矩阵计算问题,快速高效[17]。
本文中将得到的矩阵Y的每一行看作一个数据点,AP算法中相似度采用欧氏距离来度量:

自相似性一般取一个常数,本文取相似性矩阵的均值:

近邻传播算法在起始阶段将所有的样本点都看作潜在的聚类中心,并在数据点之间传递两种不同的消息:r(i,j)(responsibility)是从样本点yi发送到候选聚类中心yj的数值,用来表示yj作为yi聚类中心的代表程度,a(i,j)(availability)是从候选聚类中心yj发送到样本点yi的数值,用来表示样本yi选择yj作为聚类中心的合适程度。算法迭代过程中,这两个消息交替更新,且迭代初始化时,a(i,j)=0,更新公式为:

进行一次消息更新,也就是算法的一次迭代过程。为了避免AP算法发生大幅度震荡,引入阻尼系数λ∈[0,1),当取不同的阻尼系数时,迭代次数和迭代过程中数值的波动都会有很大不同。当选取的阻尼系数越小时,迭代次数会减少,但是迭代过程中数值的波动会很大,当图像较大时,难于收敛。当阻尼系数取值较大时,迭代次数会增加,但总体会平稳收敛,不会有较大波动,本文取值为0.9。代表矩阵R(r(i,j))和适选矩阵A(a(i,j))计算如下:

t代表迭代次数,使r(i,j)+a(i,j)取得最大值的样本yj即是样本yi的聚类中心。
基于上述改进,本文设计的算法步骤如下:
(1)随机抽取1%的样本,利用公式(8)计算相似性矩阵A和B,利用公式(15)逼近相似性矩阵W的特征向量。
(2)取k个最大特征值对应的特征向量,构造矩阵X。
(3)将矩阵X的行向量转化成单位向量构造矩阵Y。
(4)将矩阵Y中的每一行看作是子空间中的一个点,对其应用近邻传播聚类算法进行划分。
(5)如果矩阵Y第y行被划分到第j类,则对应的像素点也被划分到第j类。
4 实验与分析
本文是对传统谱聚类算法的改进,为了验证本文算法的有效性,分别应用本文算法与传统谱聚类算法对图像进行分割,比较分割效果和分割性能。实验中,尺度参数设置为σ=100,AP算法中阻尼系数λ取值为0.9,迭代次数t为40。图像方面,均选择分辨率为255×255的常用分割图像:第一组选取背景较简单的Lena图像,第二组选取前景较清晰,目标明确的Cameraman图像,第三组选取目标与背景对比不强烈的Snake图像。分割后的图像效果如图1(a)~(c)所示,其中第一列是原始图像,第二列是采用传统谱聚类算法进行分割后的图像,第三列是采用本文改进后的谱聚类算法进行分割后的图像。

图1 图像分割效果
主观上,从分割效果上来看,对于背景较简单的Lena图像,两种方法的分割效果差不多,但本文的改进算法由于加入了空间邻近信息,对于头发,帽子等纹理较复杂的区域取得了更加细腻的分割效果,而传统谱聚类算法对此方面的分割比较粗糙;对于前景较清晰,目标明确的Cameraman图像和背景与目标对比不强烈的Snake图像,由于传统的谱聚类最终采用K-means算法对简化了的向量子空间进行聚类,对初始值较敏感,产生了较多的噪点,在Cameraman图像中背景的天空和Snake图像中的石块均出现模糊现象,甚至在Snake图像中出现错分割,分割效果不理想,而使用本文改进谱聚类算法进行分割,区域一致性和边界的准确性方面得到了很大提高。
客观定量分析上,依据算法性能方面考虑,本文从两方面来评估算法性能。
(1)从运行时间方面评估:分别对比传统谱聚类和本文算法的运行时间,对每幅图像分别实验20次,记录两种算法对上述三幅图像的平均分割时间。运行时间如表1所示。
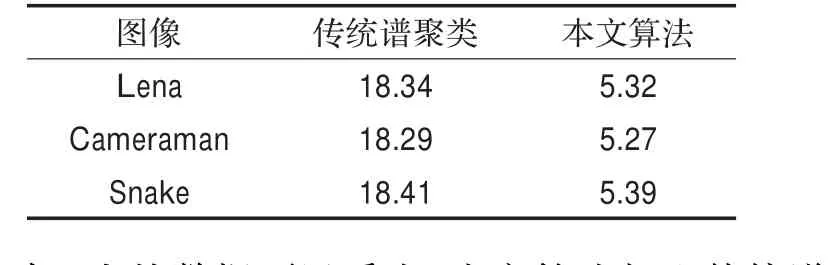
表1 两种分割算法运行时间对比s
从表1中的数据可以看出,本文算法相比传统谱聚类在运行时间上大大缩短。
(2)为了定量地评估本文算法在图像分割方面的性能优势,参考文献[1]中图像分割评价准则,本文从区域内部均匀性、区域间对比度这两方面来进行客观定量的评价。其中区域内部均匀性是指分割后的图像各个区域内部元素之间相似性,区域间对比度是指分割后图像各区域之间的相异性,这两个函数指标均是数值越大,代表的分割效果越好。指标数据如表2所示。

表2 两种算法对分割后图像的定量对比
从表2中数据可以看出,相比传统算法,本文算法分割后的图像,在区域内部均匀性和区域间对比度均得到了提高,取得了更好的分割效果。
就总体而言,本文算法在分割效果和算法性能方面都有了提升,分割效果更好,算法实用性更强。
5 结束语
本文根据传统谱聚类的不足,综合考虑了像素的空间邻近信息和特征相似性信息,定义了一个新的相似性矩阵的计算公式,在谱映射过程采用Nystrom逼近策略,大大减少了谱聚类的运算复杂度,最后对得到的低维向量子空间采用最新提出的近邻传播聚类算法进行分类,避免了K-means算法对初始值敏感和分割效果不稳定的缺陷。实验表明,新算法不仅分割效果稳定精确,而且运行时间短,性能优越。
由于本文算法仍然采用高斯核函数来度量样本点之间的相似性,尺度参数σ为实验选取,如何消除人为因素,自动确定σ或者探索一种新的构建相似性矩阵的方法将是以后研究的重点。
[1]章毓晋.图像分割[M].北京:科学出版社,2001.
[2]Zhang Tianxu,Peng Jiaxiong,Li Zongjie.An adaptive image segmentation method with visual nonlinearity characteristics[J].IEEE Trans on Systems,Man,and Cybernetics,1996,26(4):619-627.
[3]Shi Jianbo,Malik J.Normalized cut and image segmentation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(8):888-905.
[4]Odobez J M,Gatica-perez D,Guillemot M.Video shot clustering using spectral methods[C]//Workshop on Content Based Multimedia Indexing(CBMI),Rennes,2003.
[5]Malik J,Belongie S,Leung T,et al.Contour and texture analysis for image segmentation[J].International Journal of Computer Vision,2001,43(1):7-27.
[6]Chung F R K.Spectral graph theory[M].[S.l.]:American Mathematical Society,1997:227-275.
[7]Chang H,Yeung D Y.Robust path-based spectral clustering[J].Pattern Recognition,2008,41(1):191-203.
[8]王玲,薄列峰,焦李成.密度敏感的谱聚类[J].电子学报,2007,35(8):1577-1581.
[9]蔡晓妍,戴冠中,杨黎斌.谱聚类算法综述[J].计算机科学,2008,35(7):14-18.
[10]Meila M,Shi J.Learning segmentation by random walks[C]// Advances in Neural Information Processing Systems,Vancouver,Canada,2001:873-879.
[11]Ng A Y,Jordan M I,Weiss Y.On spectral clustering:analysis and an algorithm[C]//dietterich T G,Becker S,Ghahramani.Advances in Neural Information Processing Systems.Cambridge,MA:MIT Press,2002:849-856.
[12]Liang Xu.Multi way cuts and spectral clustering[R].2003.
[13]Chen Jiawei,Chen Kuanhung,Wang Jinnshyan,et al.A performance aware IP core design for multimode transform coding using scalable-DA algorithm[C]//Proceedings of International Symposium on Circuits and Systems(ISCAS),2006:21-24.
[14]Fowlkes C,Belongie S,Fan Chung,et al.Spectral grouping using the Nystrom method[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26(2):214-225.
[15]杨学鑫.改进的谱聚类图像分割方法研究[D].西安:西安电子科技大学,2010.
[16]Frey B J,Dueck D.Clustering by passing messages between data points[J].Science,2007,315(5814):972-976.
[17]管仁初,裴志利,时小虎,等.权吸引子传播算法及其在文本聚类中的应用[J].计算机研究与发展,2010,47(10):1733-1740.
GUAN Xin1,ZHOU Jilin2
1.School of Electronics and Information Engineering,Liaoning Technical University,Huludao,Liaoning 125105,China
2.Institute of Graduate,Liaoning Technical University,Huludao,Liaoning 125105,China
Aiming at the default that when the traditional spectral clustering algorithm is applied to image segmentation, it only uses the feature similarity information to construct similarity matrix and ignores the spatial adjacency information defect of spatial distribution of pixels,this paper presents a new similarity measure formula—weighted euclidean distance of the Gaussian kernel function,making full use of image feature similarity information and spatial adjacency information to structure similarity matrix.In the spectral mapping process,using Nystrom approximation strategy to approximate similarity matrix and eigenvectors,it greatly reduces the computational complexity to solve similarity matrix and reduces the memory consumption.This paper applies a new clustering algorithm—Affinity Propagation to the low-dimensional subspace.It avoids the defect that traditional spectral clustering using K-means algorithm can not automatically determine the number of clusters and it is sensitive to initial value and easy to fall into local optimum.The experiments prove that the proposed algorithm obtains better segmentation results than the traditional spectral clustering algorithm.
spectral clustering;spatial adjacency information;similarity matrix;Nystrom approximation;Affinity Propagation(AP)algorithm
A
TP391
10.3778/j.issn.1002-8331.1311-0473
GUAN Xin,ZHOU Jilin.Image segmentation based on improved spectral clustering algorithm.Computer Engineering and Applications,2014,50(21):184-188.
关昕(1967—),男,副教授,硕士生导师,主要研究方向:网络安全,图像处理;周积林(1990—),男,硕士研究生,主要研究方向:图像处理,模式识别。E-mail:zjl694059781@163.com
2013-12-02
2014-01-23
1002-8331(2014)21-0184-05
CNKI出版日期:2014-07-02,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1311-0473.html

