缩小采样区域的蒙特卡罗移动节点定位算法
陈万志,张洋,李曌成
1.辽宁工程技术大学电子与信息工程学院,辽宁葫芦岛 125105
2.渤海装备辽河重工有限公司,辽宁盘锦 124010
缩小采样区域的蒙特卡罗移动节点定位算法
陈万志1,张洋1,李曌成2
1.辽宁工程技术大学电子与信息工程学院,辽宁葫芦岛 125105
2.渤海装备辽河重工有限公司,辽宁盘锦 124010
针对无线传感器网络中移动节点定位问题,提出一种适用于未知节点移动而信标节点固定的改进蒙特卡罗定位算法,充分利用信标节点与未知节点间的测距误差来缩小采样区域,提高采样效率。仿真结果表明,改进算法在信标节点密度、连通度和节点最大运动速度等不同情况下均能提高定位精度,减少采样次数和计算量,延长网络的生存周期。
无线传感器网络;蒙特卡罗定位;移动节点;采样区域
1 引言
无线传感器网络(Wireless Sensor Network,WSN)是由大量的传感器节点组成的自组织的网络,是许多学科高度交叉的学科,可以用于许多恶劣且不适应人类工作的环境。事件发生的位置或获取信息的节点位置是传感器节点监测消息中的重要信息,没有位置信息的监测数据往往毫无意义,因此对于WSN来说,传感器节点的位置信息至关重要。因此,传感器网络节点定位技术的研究已成为WSN的研究热点和难点[1-5]。
根据定位过程中是否需要测距把定位技术分为基于测距的定位技术(TOA、TDOA、AOA和RSSI)和与测距无关的定位技术(质心定位、DV-Hop、Amorphous和APIT)两大类;以上算法均适用于固定节点定位。随着WSN技术的发展,出现了移动节点,2004年Virginia大学的HU Lingxuan等首次将用于机器人定位的蒙特卡罗算法(Monte Carlo Localization,MCL)应用在WSN移动节点定位中;随后许多学者就此提出探讨研究[6-16],文献[6]提出一种单一移动辅助种子节点的MA-MCL算法;文献[7-8]提出采用运动预测模型提高移动节点的定位精度;文献[9]将MCL与RSSI算法相结合提高采样效率;文献[10]将最小二乘法与MCL算法相结合推算未知节点在下一时刻可能的位置区域实现快速抽样和样本过滤;文献[11]提出迭代蒙特卡罗定位算法实现在信标节点数较少的情况下提高定位的准确度;文献[12]提出在移动WSN中节点间互相优化定位方法,精确锁定节点位置区域,提高采样效率和定位精度;文献[13]提出基于模糊理论的改进蒙特卡罗移动节点定位算法,在缩短定位时间的同时提高定位精度;文献[14]提出一种蚁群算法和MCL相结合的算法,在信标节点比例低的情况下提高定位精度;文献[15]提出一种距离相关的蒙特卡罗(DRMCL)算法来提高定位精度;文献[16]针对定位节点和参考节点随机运动的网络模型提出基于动态网格划分的蒙特卡罗定位算法,在定位精度、计算开销、能耗等方面都具有较好的性能。上述算法在一定程度上解决了传统MCL算法在WSN应用中的一些不足。
2 传统MCL算法
2.1 MCL算法描述
MCL算法主要有预测和过滤两个阶段。其中预测阶段主要实现对未知节点在以t-1时刻的位置lt-1为圆心,最大运动速度vmax为半径的圆中,如图1所示,随机抽取N个样本组成样本集合
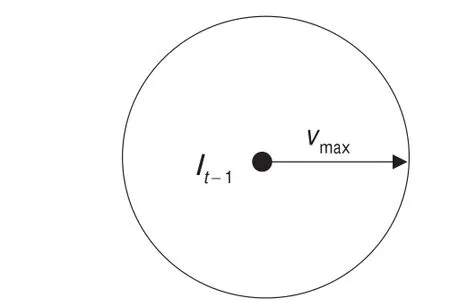
图1 MCL的采样区域
过滤阶段主要实现对传感器节点根据t时刻接收到的一跳和两跳信标节点信息,把不满足过滤条件的采样位置滤掉,其过滤条件如式(1)所示。
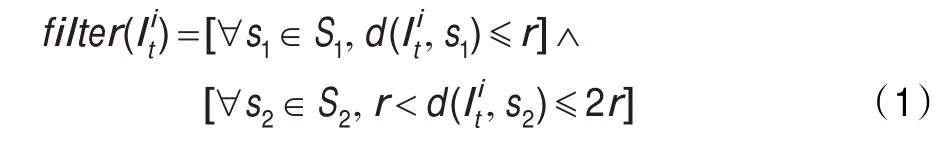
其中s1是未知节点在t时刻的一跳信标节点,S1是未知节点在t时刻的一跳信标节点集合,s2是未知节点在t时刻的两跳信标节点,S2是未知节点在t时刻的两跳信标节点集合,d(,s1)代表t时刻第i个样本与一跳信标节点间的欧几里德距离,d(,s2)代表t时刻第i个样本与两跳信标节点间的欧几里德距离,r为节点通信半径。也就是说,如果采样样本与一跳信标节点间的距离小于等于r,则该样本符合过滤条件,如图2(a)所示,反之则删除此样本;如果采样样本与两跳信标节点之间的距离大于r且小于等于2r,则该样本符合过滤条件,如图2(b)中阴影部分所示,反之则删除此样本。若过滤后留下的样本数小于N,则在采样区域循环预测和过滤两个阶段,直到留下的样本数为N。
2.2 MCL算法分析
传统MCL算法在预测阶段采集许多样本,在过滤阶段要对样本逐个进行筛选,必然导致计算量较大,若过滤后样本数少于N,则还要循环预测和过滤阶段,这样会使计算量变得更大;其原因在于有许多样本落在了位置后验密度值较小的区域中,而这些样本对估计未知节点位置的作用非常小,最终导致采样成功率降低;如果能够减小采样区域,则采集位置后验密度较大的样本自然能够很好解决上述问题。
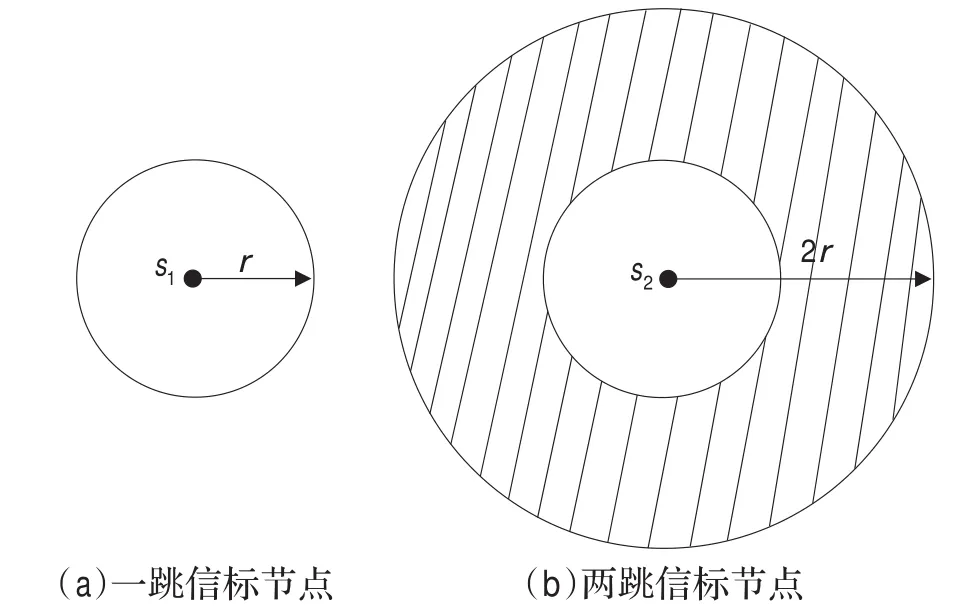
图2 过滤阶段示意图
3 DV-MCL算法
通过传统MCL算法分析和文献检索,拟提出一种缩小采样区域方法实现对MCL算法的改进,称为DV-MCL算法。其主要思路是:首先用DV-Hop算法求未知节点初始位置;然后利用未知节点与信标节点间的测距误差对移动未知节点在t时刻的位置区域进行限定,从而缩小了传统MCL算法的采样区域,提高了采样成功率和定位精度,减少了计算量和能耗,延长了网络生存周期。具体DV-MCL算法过程描述如下:
(1)初始化阶段
由于未知节点在此时尚未移动,所以网路的拓扑结构没有发生变化,因此可以把此时的移动未知节点看作固定未知节点,故用DV-Hop定位算法确定未知节点的初始位置。具体过程为:首先信标节点广播自身的位置信息到整个网络,所有节点记录到每个信标节点的最小跳数;其次,信标节点根据式(2)估算出平均每跳距离HopSizei;
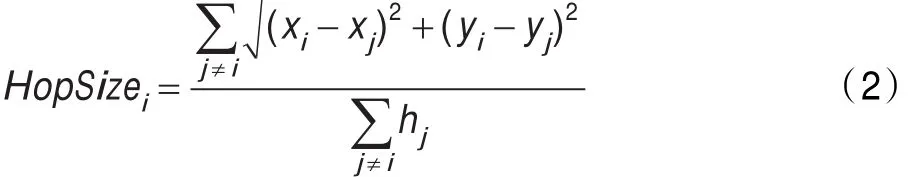
其中(xi,yi),(xj,yj)分别为信标节点i和j的坐标,hj是信标节点i与j(j≠i)之间的跳数;然后,再根据式(3)求出信标节点i和未知节点l0间的距离dil0;

其中hil0为信标节点i和未知节点l0之间的跳数;最后,选择距未知节点l0最近的三个信标节点的位置信息,根据三边测量法求出未知节点l0的坐标(xl0,yl0)。
(2)预测阶段
首先要确定采样区域;当未知节点运动到t时刻,设通信半径为r,t时刻未知节点的位置为lt,信标节点首先广播自身位置信息,如图3所示,未知节点记录到所有信标节点的最小跳数;选出距未知节点跳数最少的三个信标节点A、B、C,分别用式(4)~(6)求出它们之间的估计距离dAlt、dBlt和dClt。

图3 信标节点广播分组的传播过程

其中hAlt、hBlt和hClt分别代表信标节点A、B、C与t时刻未知节点间的最小跳数;由图3可知,t时刻未知节点与信标节点之间的实际距离小于或等于估计距离(因为用通信半径作为每跳距离会带来测距误差,一般会使估计距离略大于实际距离),因此lt以信标节点A、B、C为圆心,dAlt、dBlt和dClt为半径的三个圆内,即lt一定在圆A、B、C的相交区域内;再由图1可知,lt也一定在以t-1时刻的位置lt-1为圆心,最大运动速度vmax为半径的圆中,故lt一定在四个圆的相交区域内,如图4中的阴影区域所示。
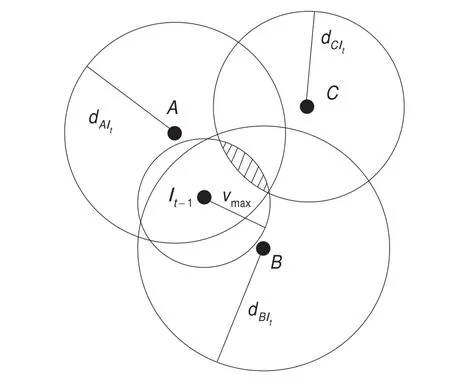
图4 DV-MCL算法的采样区域
其次,在采样区域中随机选择N个样本组成样本集合L。
(3)过滤阶段
由式(1)滤除不符合条件的采样样本,记录留下的样本数。若此时留下的样本数少于N,则重复进行采样和过滤直至留下的样本数为N。最后根据式(7)求出lt的坐标(xlt,ylt)。
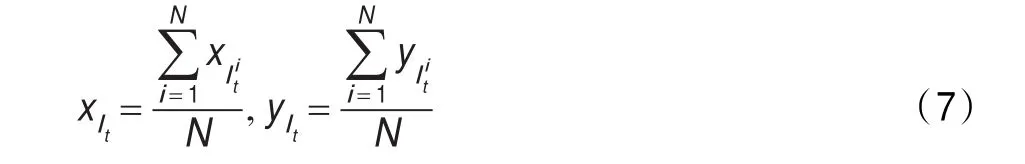
当未知节点运动到下一时刻位置,重复上述预测和过滤阶段,直到未知节点不再运动为止,定位结束。
DV-MCL算法流程图如图5所示。
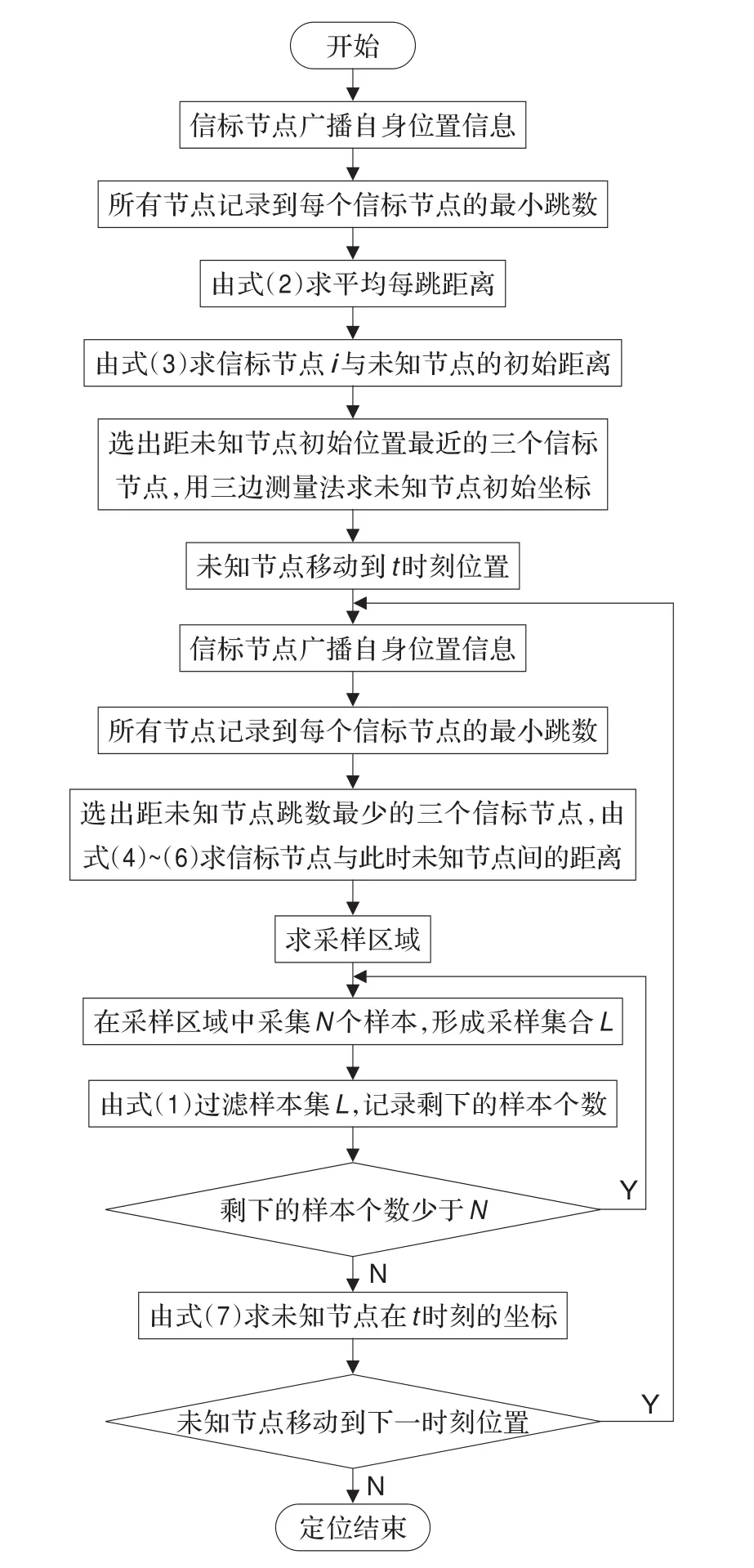
图5 DV-MCL算法流程图
4 性能仿真及分析
本文在Matlab R2013b环境下,将MCL算法、文献[8]的改进算法和DV-MCL算法在定位精度和采样次数两方面进行仿真对比。
4.1 定位精度
场景1在100 m×100 m的正方形区域内,随机布置100个传感器节点,其中40个信标节点,60个未知节点,最大运动速度vmax设定为2 m/s,采样个数N为100,定位误差e用式(8)求出。
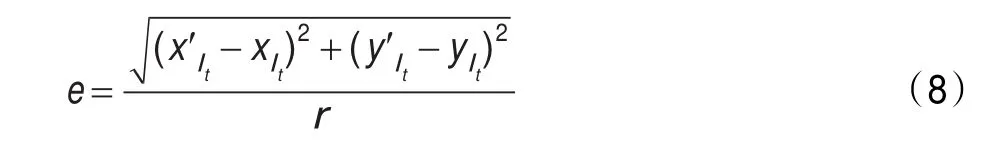
其中(x′lt,y′lt)是未知节点在t时刻的真实位置,(xlt,ylt)是未知节点在t时刻的估计位置,r为通信半径。
图6反映了第k个未知节点在不同网络连通度下的定位误差。由图6可知三种算法的定位误差均随着网络连通度增大而减小;在相同网络连通度下,DV-MCL算法的定位误差远小于MCL算法和文献[8]的改进算法。
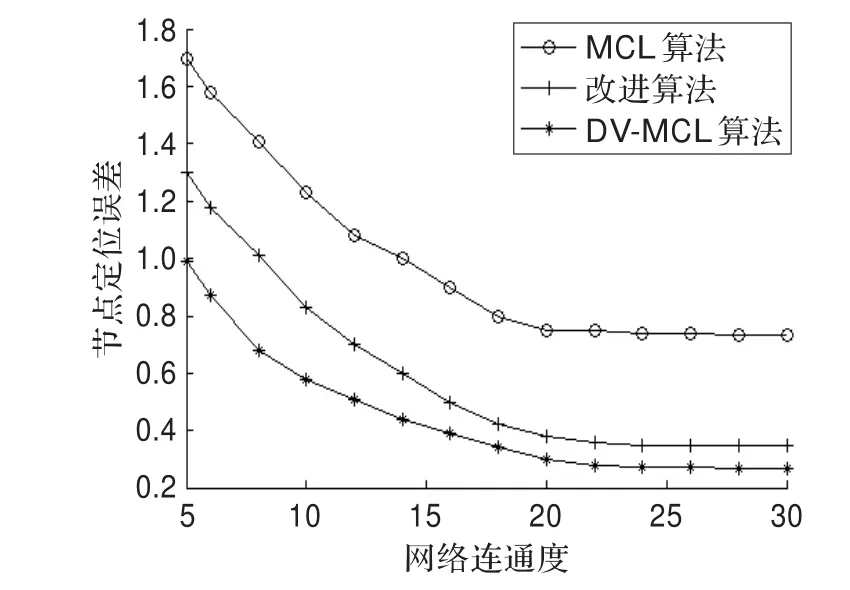
图6 网络连通度与节点定位误差间的关系
场景2在100 m×100 m的正方形区域中,随机布置100个传感器节点,其中40个信标节点,60个未知节点,采样个数N为100,通信半径r为20 m。
图7为节点最大运动速度与定位误差的关系。由图7可知三种算法的定位误差均随着vmax增加而变大,但DV-MCL算法变化较缓慢,其原因为DV-MCL算法的采样区域为图4中的阴影部分,随着vmax的增大,采样区域最大为圆A、B、C的相交处,与MCL算法和文献[8]的改进算法相比,采样区域减小的同时采样成功率提高了,故DV-MCL算法的曲线与MCL算法和改进算法的曲线相比较平滑,vmax对DV-MCL算法的定位误差影响较小;且在相同vmax情况下,DV-MCL算法的定位误差小于MCL算法和文献[8]的改进算法。
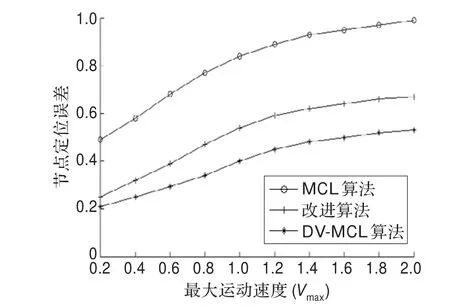
图7 最大运动速度与节点定位误差间的关系
场景3在100 m×100 m的正方形区域中,随机布置100个未知节点,采样个数N为100,通信半径r为20 m,最大运动速度为2 m/s,信标节点的个数从20~120依次增加。
图8反映出信标节点个数与节点定位误差的关系。由图8可知随着信标节点个数的增加,三种算法的定位误差均下降且总体来讲DV-MCL算法的定位误差要小于其他两种算法。原因在于随着信标节点增加,过滤条件会更准确,定位误差就会逐渐减小;同时改进算法随着信标节点数增加,在预测阶段能够选出更好的信标节点参与定位。
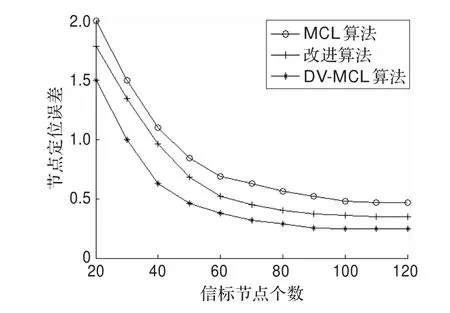
图8 信标节点个数与节点定位误差间的关系
4.2 采样次数
图9反映了场景2中,最大运动速度与节点采样次数间的关系。从图9可知三种算法的采样次数都随着vmax增大而增加,但DV-MCL算法的增加幅度较小,当vmax达到一定程度时,DV-MCL算法的采样次数逐渐稳定;在相同vmax的条件下,DV-MCL算法的采样次数比MCL算法和改进算法的采样次数少。
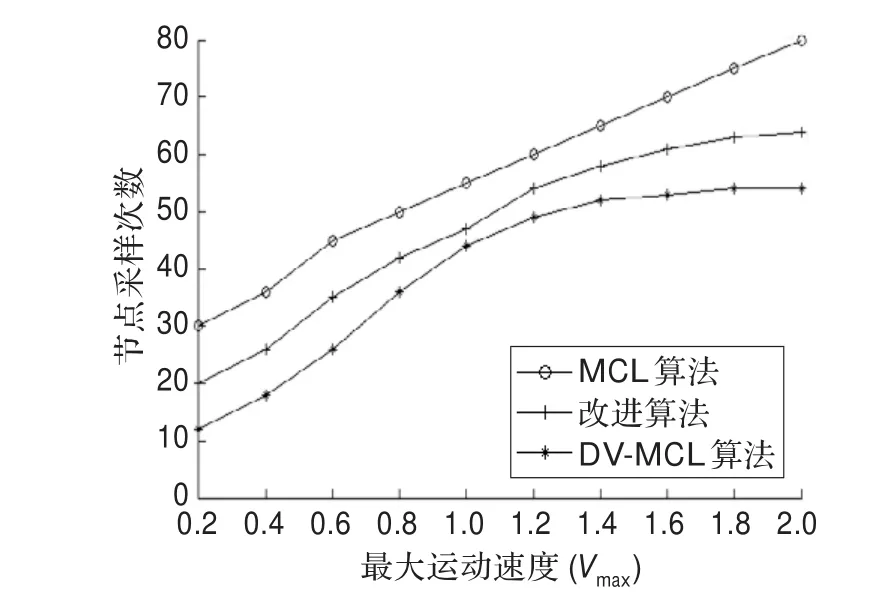
图9 最大运动速度与节点采样次数间的关系
5 结束语
在用固定节点定位算法求出移动未知节点初始位置的同时,提出了一种缩小采样区域的方法对原MCL算法进行改进。经仿真可知,通过DV-Hop算法求未知节点的初始位置,可以提高初始位置的准确性;在较小的采样区域中采样,可以提高采样成功率,减少采样次数和计算量,确保了算法效率,同时延长了网络生存周期,增加了定位精度;算法适用于未知节点移动而信标节点固定的WSN网络。
[1]孙立民,李建中,陈渝,等.无线传感器网络[M].北京:清华大学出版社,2005:135-136.
[2]唐鹭,洪月华,伍华健.无线传感器网络节点定位综合算法[J].计算机工程与应用,2010,46(4):86-88.
[3]黄晓利,王福豹,段渭军,等.基于在线校正的无线传感器网络定位算法[J].计算机工程与应用,2008,44(6):133-135.
[4]卫开夏,田金鹏,王克谦.无线传感网络DV-Hop定位改进算法[J].传感技术学报,2010,23(12):1820-1823.
[5]刘辉亚,徐建波.无线传感器网络分布式的移动节点定位研究[J].计算机工程与应用,2010,46(1):72-76.
[6]Teng Guodong,Zheng Kougen,Dong Wei.MA-MCL:Mobile-Assisted Monte Carlo Localization for Wireless Sensor Networks[J].International Journal of Distributed Sensor Networks,2011,2011.
[7]李敏,罗挺,徐华.一种基于参考节点选择模型的无线传感器网络定位算法[J].传感技术学报,2011,24(2):264-268.
[8]黄梅根,常新峰.一种基于蒙特卡罗的无线传感器网络移动节点定位算法研究[J].传感技术学报,2010,23(4):562-565.
[9]朱海平,于红丞,钟小勇,等.动态无线传感器网络的改进蒙特卡洛定位算法[J].传感技术学报,2012,25(9):1284-1288.
[10]刘志华,李改燕,刘晓爽.基于最小二乘法的蒙特卡洛移动节点定位算法[J].传感技术学报,2012,25(4):541-544.
[11]董齐芬,俞立,陈友荣,等.移动无线传感网中的迭代蒙特卡罗定位算法研究[J].传感技术学报,2010,23(12):1803-1808.
[12]梅举,陈涤,辛玲.基于蒙特卡洛方法的移动传感网节点定位优化算法[J].传感技术学报,2013,26(5):689-694.
[13]李建坡,时明,谢岩,等.一种基于模糊理论的蒙特卡洛移动节点定位算法[J].计算机应用与软件,2013,30(12):147-150.
[14]王培东,祁春莉.一种改进的节点定位方法[J].计算机应用与软件,2012,29(8):242-244.
[15]彭保,顾学迈,丁博.动态传感器网络中距离相关的蒙特卡洛定位算法[J].科学技术与工程,2008,8(18):5301-5303.
[16]魏叶华,李仁发,罗娟,等.基于动态网格划分的移动无线传感器网络定位算法[J].计算机研究与发展,2008,45(11):1920-1927.
CHEN Wanzhi1,ZHANG Yang1,LI Zhaocheng2
1.School of Electronics and Information Engineering,Liaoning Technical University,Huludao,Liaoning 125105,China
2.China Petroleum Liaohe Equipment Company,Panjin,Liaoning 124010,China
In response to the problem of mobile node position for WSN,an improved MCL algorithm for mobile unknown node and fixed beacon node is proposed.Sampled area is reduced to improve the sampling efficiency by using the ranging error of beacon node and unknown node sufficiently.The simulation results show that the improved algorithm can improve the localization accuracy,reduce the number of sampling and computation,and prolong the network life cycle in different conditions of the beacon node density,connectivity and the maximum velocity of node.
Wireless Sensor Network(WSN);Monte Carlo Localization(MCL);mobile nodes;sampled area
A
TP393
10.3778/j.issn.1002-8331.1403-0363
CHEN Wanzhi,ZHANG Yang,LI Zhaocheng.Monte Carlo localization algorithm for mobile node by reducing sampled area.Computer Engineering and Applications,2014,50(21):106-110.
陈万志(1977—),男,在读博士,副教授,CCF会员,研究领域为人工智能、计算机过程控制、物联网应用等;张洋(1989—),女,在读硕士研究生,研究领域为无线传感网络、计算机过程控制等;李曌成(1937—),男,助工,研究领域为计算机控制及电气安全。E-mail:chenwanzhi@lntu.edu.cn
2014-03-25
2014-05-10
1002-8331(2014)21-0106-05
CNKI出版日期:2014-07-02,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1403-0363.html

