逐步贝叶斯判别分析中的变量优化方法研究

胡建鹏，陈强，黄容

上海工程技术大学电子电气工程学院，上海 201620

逐步贝叶斯判别分析中的变量优化方法研究

胡建鹏，陈强，黄容

上海工程技术大学电子电气工程学院，上海 201620

判别分析中特征变量是影响判别结果的决定性因素，选取适当的特征变量组合可以提高正判率、减少计算量。介绍了贝叶斯判别和逐步判别法的基本原理，分析了目前出现的一些特征变量优化方法，以油气解释评价中的贝叶斯判别应用为例，对于逐步贝叶斯判别中的变量优化方法进行了研究和总结，提出了变量的多步优化策略和分步多模型优化策略，包含了从变量范围选择、数据预处理、特征变量提取到初步筛选和逐步判别的完整过程，使得正判率不断优化，最终得到了较为满意的判别结果。

贝叶斯判别；逐步判别；变量优化；判别因子；气测录井

1 引言

贝叶斯（Bayes）判别是经典的判别分析方法，既考虑到各个总体出现的先验概率，又考虑到错判造成的损失，这是相较于其他判别方法的优点所在，其判别效果比较理想，应用也非常广泛，尤其是在地质和勘探领域[1-4]。判别分析是要根据不同类别所提取的特征变量来建立待判样品归属于哪个已知总体的数学模型，要对待判样品做出正确的归类，首先要获取样本总体及待判样品的特征变量，然后对总体及待判样品事物的特性进行变量指标的描述，进而判别待判样品的归属。由此可知，特征变量的优化是判别分析中的一个重要问题，是判别效果优劣的关键，例如在某个判别问题中，如果将其中主要的指标忽略了，由此建立的判别函数其效果一定不好；另外在判别分析中，不是特征变量越多越好，较多的变量个数增大了建立判别函数需要的计算量，同时，因为特征变量之间的不独立性及判别方程组的阶数太高，可能导致计算精度下降，甚至出现病态[5]，在排除了变量之间的相关性之后选择适当的变量个数是较好的解决方案。因此要获得理想的判别效果，判别变量的选取和优化就显得非常重要。

在判别分析的特征变量优化问题上，连承波等[2]利用R型因子分析对特征变量进行降维分析，在参数大部分信息不丢失的情况下，对11个气测参数优化组合降维，提取了4个气测解释综合参数，然后利用加权灰色关联分析方法进行储层含油气性识别，得到了较高的正判率，该方法R型因子分析模型的精确度对于标准模型库的代表性要求较高，对最终正判率的影响较大。刘宏杰等[6]利用一种基于粗糙集属性约简的方法对特征变量进行优化选择，充分利用粗糙集属性约简不需要属性分布的先验信息这一特点，再使用贝叶斯判别法来进行油气储层预测，正确率较高，该方法使用了很少的样本进行属性约简，对于样本的挑选就显得很重要，在连续属性离散化时，临界值的确定也非常关键，少量样本的代表性和临界值的精确度决定了模型的正判率。武晓岩等[7]应用随机森林逐步判别方法，对三类癌症的基因表达数据进行变量筛选，建立随机森林模型，仅用较少数目的基因就可以实现它们的判别分类，这种方法对于成千上万个基因作为特征变量的判别问题十分有效，计算时间也较长。相较于以上所提及的较新的特征变量优化方法，传统的逐步判别法的应用还是最广泛，同时也是最成熟的[8-11]，而同样是进行基因微阵列数据的降维，荀鹏程[12]等使用的三步降维策略来进行判别分析，进一步提高了降维效率和正判率，其中第三步就是使用的逐步判别法。逐步判别分析是一种能自动剔除变量，挑出必要的、较好的指标建立判别函数的方法，有利于判别结果的稳定性和提高判别能力[11]；但是如果不加判断盲目使用此方法或者不联系相关领域知识将问题看作纯粹的数学问题的话都可能会使判别结果不够理想，甚至出现难以解释的出乎意料的结果。本文总结了逐步贝叶斯判别法中变量优化的要点，并引入相关文献的降维思想，提出多步和分步实施的策略，使得变量优化的效果更加明显。

2 贝叶斯判别的原理和应用

2.1 基本原理

贝叶斯判别分析[13]是根据已掌握的每个类别的若干样本的数据信息，总结出客观事物分类的规律性建立判别函数，然后，根据总结的判别函数，就能够判别新样本函数所属类别，对于一个待判样品(x1，x2，…，xp)，判别它属于已知m组中何组的方法，是计算样品属于其中某一组的条件概率P(l|X)(l=1，2，…，m)，比较这m个概率的大小，将该样品归入概率最大的一组。设有总体Gi(i=1，2，…，m)，Gi具有概率密度函数fi(x)。并且根据以往的统计分析，知道Gi出现的概率为qi。即当样本x0发生时，求它属于某一类的概率。判别规则：若

则x0判给Gl。在正态的假定下，fi(x)为正态分布的概率密度。当Gi～Nm(μi，Σi)时有：假设k个总体的协方差阵相同，判别函数可化简为：

2.2 贝叶斯判别应用于油气解释评价

贝叶斯判别在石油和天然气勘探领域的应用十分活跃，尤其是在储层流体性质识别和预测的问题上，这是录井解释评价的核心，传统录井现场油气评价技术中多采用人工经验和图版、图表分析法。录井解释的途径有很多，气测、地化、核磁、定量荧光、X射线荧光（XRF）以及综合录井分析等方法可以获取很多原始测量数据，能提取的特征变量可以达到上百个，这些变量可以按照获取途经的不同分别进行解释评价，也可以联合起来进行综合分析，以气测解释为例，根据文献[1，10]的经验，选择采用全烃含量TC、全烃背景值Cb、甲烷C1、乙烷C2、丙烷C3、异丁烷iC4、正丁烷nC4这些原始数据直接应用到贝叶斯判别法中，对湖北江陵探区一批录井数据进行判别，原始数据如表1所示。

表1 样本原始测量数据1）

将30个样本分为油（气）层、含烃水层和干层3类总体（各10个样本），通过训练后求出判别函数，将样本数据回代到判别模型中，得到的综合正判率只有63.3%，只有水层的正判率达到了90%，另外两类总体的正判率都只有50%，这样的判别效果肯定是不能接受的，究其原因，是因为地质条件的不同会导致储层含油气性类型对应气测指标分布特征的差异，如果直接使用其他地方的判别模型或选取类似的特征变量在录井解释领域是绝对行不通的，贝叶斯判别方法本身是没有问题的，关键是特征变量的优化。一般来说，在录井解释的实际现场应用过程中，合适地使用贝叶斯判别法可以使正判率达到70%至95%之间。

3 变量的多步优化策略

逐步判别法是挑选特征变量的最常用方法，其基本原理是在已知预判别的类型和数目，并已取得各种类型的一批已知样品的情况下，根据各变量在分类判别式中作用的大小进行排序，并逐步地选入判别式中，直到既无变量选入，又无变量剔除为止，最后计算出相应的判别函数和评价对象从属各类的概率值，实现判别分类[4]。但是特征变量的优化不只是逐步挑选变量，应采用多个优化步骤。

3.1 特征变量的范围选择

在原始样本数据中，会存在很多可选变量，但并不是所有变量都与判别有关，以气测解释数据为例，表1中列出了最常用的气测解释变量，其中包含相邻盖层钻时ROPn与储层最小有效钻时ROPs，另外还包含有异戊烷、正戊烷、硫化氢、氢气以及二氧化碳的测量值，但是后五种在做油气解释评价时意义不大，异戊烷、正戊烷、硫化氢、氢气经常在大部分井段是不能明显检出的，而二氧化碳在不同含油气性储层类型中的含量都差不多，故不在选择范围之内。因此，特征变量的范围选择要根据行业知识和经验进行，将有可能与判别相关的变量一并选入，第一步选择范围可以稍微大一些。

3.2 特征变量预处理和特征参数提取

样本原始的测量数据有时候并不是直接应用与判别，不同变量量纲不同，量级也有很大差别，如表1中各种烃含量均是百分比，其值较小，而ROP钻时的值均较大，所以有必要将各烃含量值放大，文献[1]为了消除不同录井仪器检测数据绝对含量上的差异，也有将数据放大的处理方式，同时计算不同烃含量的比值，将绝对含量转化为相对含量，在这里将各烃相对含量的数据放大100倍。

除了数据的预处理以外，根据行业知识与经验，还可以引入一些基于原始测量数据的特征参数，如文献[2]将胜利油田桩海地区的气测信息转化为11个气测参数，如烃气平衡：X1=（C1+C2）/（C3+iC4+nC4）和烃气湿度比：X2=（C2+C3+iC4+nC4）/C1等参数。在传统的气测解释评价方法中，流体性质识别的最常用的就是交会图解释，如钻时比值与烃对比系数交会图和轻烃比值[C1/C2-C1/C3]解释图版等，其中用到的重要参数就有钻时比值ROPn/s，是指相邻盖层钻时ROPn与储层最小有效钻时ROPs之比，反映储层孔隙性的相对变化；烃对比系数Kc是指全烃显示值与基值或背景值之比，反映储层含油性的相对变化。因此本文按照此类经验，在原始测量数据基础上提取特征参数ROPn/s、Kc、C23（C2/C3）和niC4（nC4/iC4）作为特征变量，求比值时若分母为零，设定比值为1。

3.3 特征变量初步筛选

将处理过的原始数据和提取的特征参数组合在一起，组成了待选特征变量，需要进行组间均值检验，并用Wilk’sλ统计量对每个判别变量单独检验其判别能力；对于显著性检验，可进行普遍使用的F检验，检验结果相当于分组变量和判别变量间的简单方差分析[14]。本文对上述所有特征变量进行了组间均值检验，结果如表2所示，Wilk’sλ统计量是组内离差平方和与总离差平方和的比，值的范围在0到1之间，值越小表示组间有很大的差异，值接近1表示没有组间差异。表2按照Wilk’sλ统计量从小到大排列，说明变量ROPns的单独判别能力最强，而当某个变量的显著性水平小于常用的置信水平（一般设为0.05），就有足够理由拒绝“组间均值没有差异”的假设，说明组间均值过于接近，很难区分，这样的特征变量应该考虑剔除掉，如表2中的最后4个变量；但是这也不是绝对的，由于判别变量间可能相互关联，尽管某些变量本身具有较小的判别作用，但在与其他变量联合后对于判别效果的提高也可能有较大的贡献。

另外作为判别分析的特征变量应该相互独立，避免冗余和相互干扰，故应该对特征变量进行相关性分析，尤其是在部分特征参数的提取过程中，使用了较多的相对比值和原始数据混合在一起的情况，若两个变量之间的相关系数大于0.9，则应考虑是否二者选其一，这里使用的是合并的组内相关矩阵，是通过计算各组分离的相关矩阵的平均值而获得的。表3显示了特征变量的相关矩阵，篇幅所限，只列出了部分变量，其他未列出变量的相关系数绝对值均没有超过0.8，其中可以看出ROPn和ROPs相关系数达到了0.94，TC和KC的相关系数达到了0.96，但是TC和KC的独立判别能力都是比较强的，通过实验表明二者结合加入判别时的判别效果更好。

表3 判别变量相关矩阵

综合组间均值检验和变量间相关性分析的结果，决定剔除掉ROPn和Cb两个变量，在进行逐步判别之前保留11个变量。

3.4 逐步判别挑选变量

所谓变量择优算法则是采用有进有出的算法，即每一步都要对变量的附加信息进行检验，使其优胜劣汰。其原理和计算步骤不再赘述，可参照文献[13-14]，挑选变量的依据是对其判别能力的衡量，有多种准则可以选择[15]。

（1）Wilk’sλ准则：在每一步挑选使得Wilk’sλ最小的变量进入判别模型，对于每个候选判别变量都要计算F统计量，与Wilk’sλ统计量成反比，即具有最大F值的变量进入判别模型，F值由下式计算：

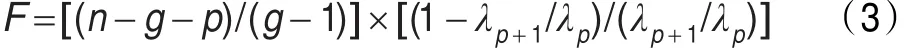
公式（3）中，n为样本数，g为类别数，p为变量个数，λp为添加变量以前的Wilk’sλ值，λp+1为添加变量以后的Wilk’sλ值。

（2）马氏距离（Mahalanobis Distance）准则：在计算的每一步中，使两个相邻类别之间最近的马氏距离最大的变量进入判别模型。组a和组b之间的马氏距离由下式定义：

公式（4）中i和j从1到p求和，p为变量个数，g为组数，为第a组第i个变量的均值，为第b组第i个变量的均值，为协方差矩阵的逆矩阵的元素。

（3）Rao’s V准则：每步都是使Rao’s V统计量产生最大增量的变量进入判别函数。可以对一个要加入到模型中的变量的V值指定一个最小增量。当某变量导致的V值增量大于指定值时才进入判别函数。Rao’s V又称为Lawley-Hotelling迹，用下式定义：

公式（5）中i和j从1到p求和，k从1到g求和，p为变量个数，g为组数，nk为第k组的样本大小，为第k组第i个变量的均值，为组内协方差矩阵的逆矩阵元素。

应用以上3种准则分别对含11个变量的30个样本数据和36个待判数据进行逐步判别，这里需设定F门槛值，即对于每一步按照规则挑选的变量，其判别能力由公式（3）中计算的F值必须大于F门槛值才能引入到判别模型当中，F门槛值的设定直接决定了入选变量的数量，这里设定添加变量的F值为2.0，剔除变量的F值为1.8，三种不同规则的逐步判别结果如表4所示，Wilk’sλ准则和Rao’sV准则挑选出来的变量组合是完全一致的，所以判别结果也一致，在计算步骤当中就可以看出，Rao’sV值基本上与F值成正比，F值最大的变量其Rao’sV值也最大；而马氏距离准则挑选了更多的变量，也获得了更好的判别效果。

表4 不同判别规则判别结果

上述三种判别准则主要思想都是建立一个基于这些总体的目标函数，然后通过对这个函数值来判断总体间的差异程度，除此之外还有利用统计距离定义的总体可分性函数[16]，它的增值可以反映变量区分总体的显著程度，一个能显著区分总体的变量会带来大的增值，可以用于判别总体间区别相对较小的情况。综合来讲，Wilk’sλ准则使用最为广泛，在区分最难判别的组别时可以考虑使用马氏距离准则，而对于备选变量存有疑虑的话，可使用Rao’sV准则，此准则可以再增加一个门槛值。通过设置合适的F门槛值，利用多步优化策略对本文实例进行判别，最终回代正判率和待判数据正判率分别为96.7%和83.3%。

通过对于特征变量优化方法的研究，得出以下结论：

（1）特征变量的优化对于判别结果起着至关重要的作用，特征变量的优化不是简单地使用逐步判别法，而是从范围选择、数据预处理、特征变量提取到初步筛选和逐步判别的完整过程。

（2）特征变量的个数既不是和正判率成正比也不是成反比，对于确定的训练样本，特征变量的个数到达某个值或是某个区间时正判率最佳。一般来说，在去除了变量相互影响的前提下，特征变量越多，正判率越高；若特征变量冗余且相关性较高时，剔除一些特征变量反而能提高正判率。

（3）逐步判别法使用不同的F门槛值和不同的判别准则决定了选取特征变量的个数，F门槛值越低，选出的变量个数越多；不同的判别准则适用于不同情况，其实质是在逐步判别的过程中用不同的方法衡量变量的判别能力，不仅决定着入选的变量个数，也决定了变量的组合，从而影响最终判别结果。

（4）逐步判别法筛选出的特征变量组合不一定是相同数量变量组合中的最优，因为每次引入新变量都是在保留已引入变量的基础上进行，然后有些变量还在引入后被剔除了。特征变量的独立判别能力并不能直接决定其去留，独立判别能力弱的变量加入组合后也能明显提高正判率，特征变量的优化在于寻找最优变量组合。

4 分步多模型变量优化策略

通过对逐步判别过程的分析，发现不同的变量区分不同组别时的能力各有不同，根据组间最近马氏距离最大值可以衡量这种能力，表5显示了在一次逐步判别的最后阶段，已入选的9个变量所对应的组间马氏距离最大值，一部分变量更适合区分第1和第2类总体，另外的则适合区分第2和第3类总体，依照这种情况，可以考虑将三类总体先合并成两类总体，例如将上述实例中的总体划分为油（气）层和非油气层，利用一次逐步贝叶斯判别先把油（气）层从所有样本中区分开来，然后在判定为非油气层的样本中再用一次判别把干层和含烃水层分开。

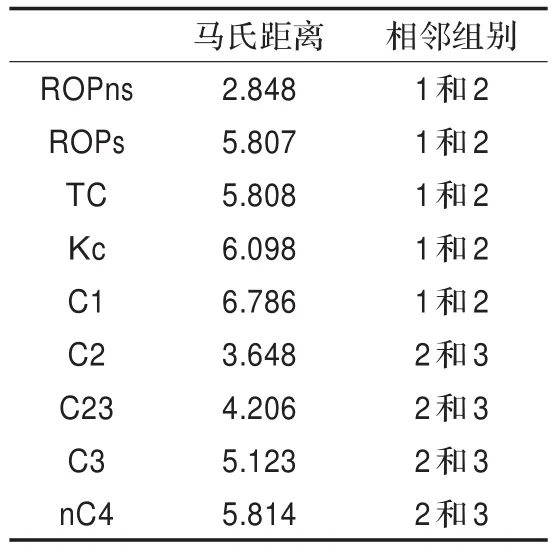
表5 判别变量与组间马氏距离

这样做的实质是先用一个贝叶斯判别模型将所有待判样本划分为若干子集，然后在各个子集中再用判别模型将各个总体区分开来，对于3至5个总体来说，两三步判别即可得出结果，而且可以在分步实施的各个判别模型中选用对于不同组别判别能力较强的不同判别变量组合，也可以选择不同的判别准则，可以得到较好的判别效果。表6显示了分步判别的结果数据，综合两步的判别结果，最终统计36个待判样本误判6个，总的正判率也达到了83.3%。

表6 分步多模型逐步判别结果

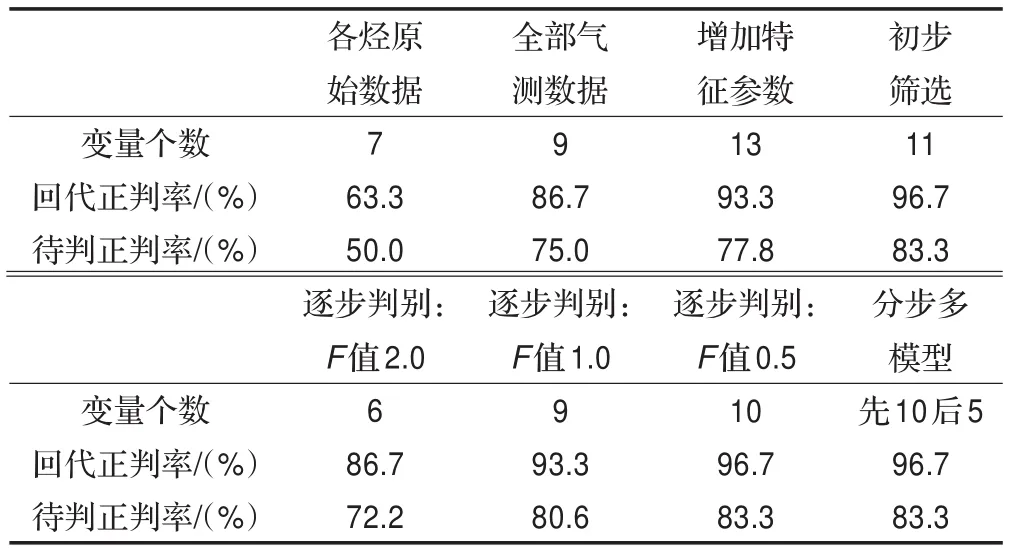
表7 优化过程中不同阶段和不同方法的判别结果

5 结束语

通过对贝叶斯判别中的特征变量进行不断的优化，使得正判率稳步提高，表7显示了优化过程中不同阶段和不同方法的判别结果，比较说明本文提出的多步优化策略和分步多模型优化策略均具有较好的优化效果。多步优化策略是在总结和分析已有的优化方法的基础上提出的一套综合性较强的变量优化方法，包含了从变量范围选择、数据预处理、特征变量提取到初步筛选和逐步判别的完整过程，适用于包含油气解释在内的诸多领域；而分步多模型优化策略的提出是利用了变量在判别不同总体分类时各有所长的特点，对于某些特定的总体分类可以取得不低于多步优化的正判率，但若总体数较多，采用分步多模型优化策略会增加计算量，此时可考虑部分使用该策略。

[1]郭晖，骆福贵，倪有利，等.Bayes多母体判别模型在油气层评价中的应用[J].录井工程，2010，21（2）：5-7.

[2]连承波，钟建华，李汉林，等.气测参数信息的提取及储层含油气性识别[J].地质学报，2007，81（10）：1339-1443.

[3]魏治文，方坤河，杨华山，等.贝叶斯（Bayes）判别分析在粉煤灰分类中的应用[J].粉煤灰综合利用，2006（6）：11-13.

[4]陈红江，李夕兵，刘爱华.矿井突水水源判别的多组逐步Bayes判别方法研究[J].岩土力学，2009，30（12）：3655-3659.

[5]陈辉，郭科.判别分析中的变量择优及其MATLAB实现[J].河南师范大学学报：自然科学版，2004，32（1）：12-16.

[6]刘宏杰，冯博琴，李文捷，等.粗糙集属性约简判别分析方法及其应用[J].西安交通大学学报，2007，41（8）：939-943.

[7]武晓岩，闫晓光，李康.基因表达数据的随机森林逐步判别分析方法[J].中国卫生统计，2007（2）：151-154.

[8]孟凡奇，李广杰，李明，等.逐步判别分析法在筛选泥石流评价因子中的应用[J].岩土力学，2010，31（9）：2925-2929.

[9]段新国，王允诚，李忠权，等.应用多组逐步判别分析优选油气层[J].大庆石油地质与开发，2007，26（1）：68-71.

[10]龙铄禺.应用逐步判别法建立气测解释模型[J].录井技术，1999（3）：22-28.

[11]毕淑峰，朱显灵，马成泽.逐步判别分析在中国烤烟香型鉴定中的应用[J].热带作物学报2006，27（4）：104-107.

[12]荀鹏程，钱国华，富春枫，等.判别分析驱动的微阵列数据的降维策略[J].中国卫生统计，2009（2）：147-149.

[13]任雪松，于秀林.多元统计分析[M].2版.北京：中国统计出版社，2011.

[14]Backhaus K，Erichson B，Plinke W，et al.Multivariate statistical analysis[M].Berlin：Springer，2005.

[15]苏金明.统计软件SPSS 12.0 for Windows应用及开发指南[M].北京：电子工业出版社，2004.

[16]潘志文，汪国强.判别分析中基于总体可分性的变量选择[J].华南理工大学学报：自然科学版，2001，29（11）：81-84.

HU Jianpeng,CHEN Qiang,HUANG Rong

School of Electrical&Electronic Engineering,Shanghai University of Engineering Science,Shanghai 201620,China

Characteristic variables selection is a critical factor that affects the result of discriminant analysis.Appropriate selection of variable combination can improve the correct rate and reduce the amount of computation.This paper introduces the basic principle of Bayes discriminant and stepwise discriminant method,analyses some methods of characteristic variables optimization at present,takes application of Bayes discriminant in oil gas interpretation and evaluation as an example to research on variable optimization method in stepwise Bayes discriminant analysis,and puts forward a variable step optimization strategy and a multi-model optimization strategy,including variable range selection,data preprocessing,feature extraction,preliminary screening of variables and stepwise discriminant,which makes correct judgement rate optimized gradually,and obtains more satisfactory discriminant result.

Bayes discriminant;stepwise discriminant;variable optimization;discriminant factor;gas logging

A

TP391

10.3778/j.issn.1002-8331.1211-0277

HU Jianpeng,CHEN Qiang,HUANG Rong.Study on variable optimization method in stepwise Bayes discriminant analysis.Computer Engineering and Applications,2014,50（21）：63-67.

上海工程技术大学科技发展基金项目（No.2011Q07，No.2011Q06）；上海工程技术大学学科专业建设项目（No.XKCZ1212）。

胡建鹏（1980—），男，讲师，CCF会员，研究方向：计算机应用；陈强，博士，教授，研究方向：数值分析和计算机图形学。E-mail：mr@sues.edu.cn

2012-11-23

2013-05-10

1002-8331（2014）21-0063-05

CNKI出版日期：2014-01-15，http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1211-0277.html