基于气体组成的天然气压缩因子计算方法①
梁光川 左 果
(西南石油大学石油与天然气工程学院)
无因次量天然气压缩因子在天然气工程计算中是最重要的物性参数之一。而获取压缩因子的方法目前主要有:查Standing-Katz(SK)图法、实验法、状态方程计算法[1]和经验公式法。SK图法只适用于低分子量的甜气,其误差在2%~3%[2],而当混合气体为高分子量或酸气时,其准确度将大大降低;实验法具有费用昂贵、耗时的缺点。此外,根据实验样本所获得的压缩因子,对另一种不同组成的气体来说,其实验数据将不可用。因此,使用经验公式或状态方程来计算压缩因子在天然气工业中是十分必要的。
1 公式计算气体压缩因子
用公式计算天然气压缩因子大体可分为两种方法:一种是在混合气体组成已知的条件下,求得压缩因子;另一种是通过气体的相对密度等物性值来求得压缩因子。以下要介绍和对比的是基于气体组成来求得压缩因子的计算关系式。
1.1 伪临界参数的计算关系式
当混合气体组成和相应单一组分的临界压力及温度已知时,便可求得其伪临界压力和温度。这里临界压力和临界温度表示的是单一气体的物性,而伪临界压力和伪临界温度则是针对混合气体来说的。同时,伪临界参数又可称为拟临界参数或虚拟临界参数。表1显示了某些单组分的Tc和pc值。
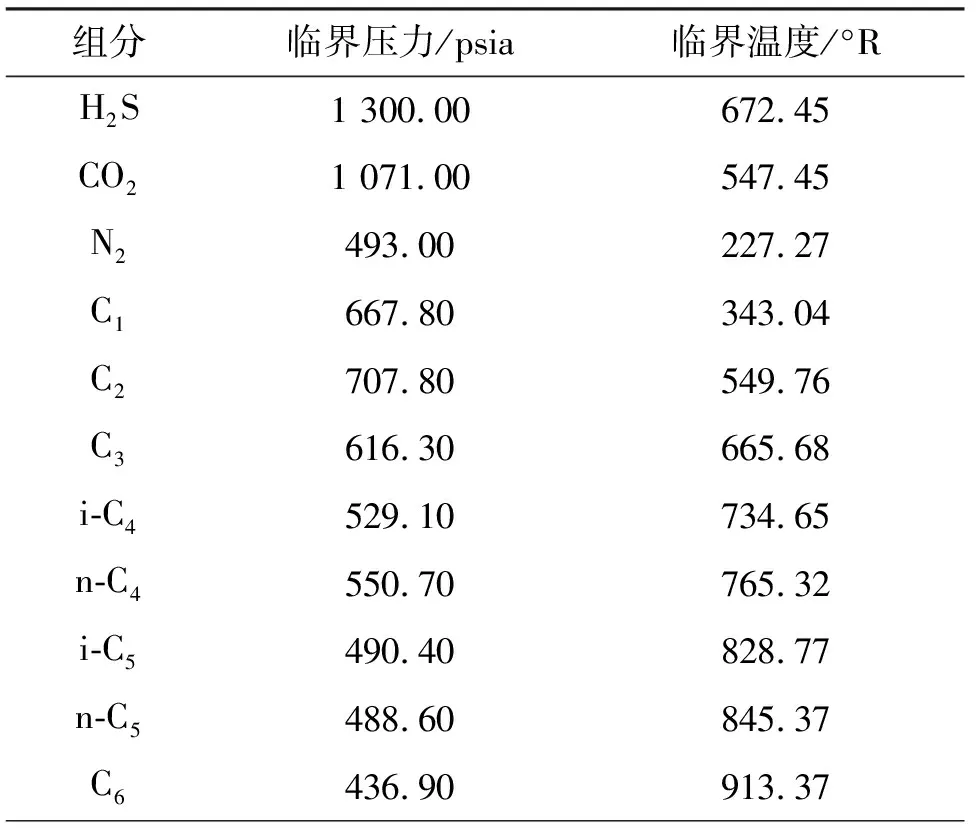
表1 天然气各组分的临界参数
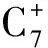
(1)
(2)
(3)
(4)
式中,J为SBV参数,°R/psia;K为SBV参数,°R/psia0.5;yi为组分的摩尔分数(C1~C6);Tc为临界温度,°R;pc为临界压力,psia;Tpc为伪临界温度,°R;ppc为伪临界压力,psia。
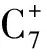
(5)
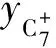
2000年,Adel M. Elsharkawy[2]提出了与L.D. Piper混合法则相似的方程,他在方程中也同样考虑了非碳氢成分和庚烷及以上组分的影响。但Elsharkawy方程在计算伪临界参数时,使用的是临界参数而非其相对分子质量。同时,方程中所包含的常数更少。其方程式如下:
(6)
式中,α、β为常数。
将式(5)和式(6)分别代入式(3)和式(4)便可以得到相应的伪临界参数。
1.2 压缩因子的计算关系式
天然气压缩因子的计算方法包括Dranchuk-Abou-Kassem(DAK)方程、AGA8-92DC方程和Mahmoud方程。
1975年,P.M.Dranchk 和J.H.Abou-Kassem 在Benedict-Webb-Rubin 1940提出的状态方程的基础上提出了DAK方程[6]。该方程能通过迭代求解的方法求得一定条件下气体的压缩因子,其计算值与SK图相比较,误差小于0.000 1[7]。计算压缩因子的DAK方程是对比压力和对比温度的函数,其计算形式如下:
(7)
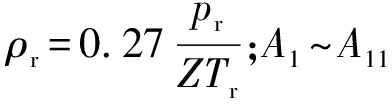
(8)
(9)
式中,T为绝对温度,°R;p为绝对压力,psia。
另外,根据对应态原理可知,处于不同温度和压力条件下的两种气体,如果它们的对比温度和对比压力相等,则它们的气体压缩因子相等[8]。
1992年,美国燃气协会发表了以状态方程为基础计算压缩因子的AGA8-92DC方程。该方程包含了58种物质的状态方程参数,21种识别组分的特征参数,21种识别组分的二元交互作用参数。其应用范围主要是管输气,绝对压力为0~12 MPa,温度为263~338 K[9],其压缩因子计算关系式如下:
(10)
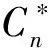
对比密度同摩尔密度相关,两者的关系如下:
ρr=L3ρm
(11)
式中,L为混合物体积系数,(m3/kmol)1/3。
(12)
式中,p为绝对压力,MPa;R为摩尔气体常数,0.008 314 510 MJ/kmol·K;T为热力学温度,K。
M.A. Mahmoud[7]经过对压缩因子实测数据的拟合与修正后,得到了相关经验式,并将同等条件下的计算结果在SK图上进行验证,于2013年提出了中高压条件下求解压缩因子的方程,见式(13):
(13)
式中,e为自然对数的底数 (e=2.718…)。
由上可得到5个基于气体组成来求解Z的方程,分别是AGA8-92DC、Piper-DAK、Piper-Mahmoud、Elsharkawy-DAK与Elsharkawy-Mahmoud方程。
1.3 基于气体组成求得压缩因子
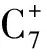
将以上提及的5个压缩因子计算方程式分别写入visual basic 6.0 program(VB),并使用同一台电脑,意在保持相同的计算机引入误差。另外,需提及的是,因方程(7)和(10)两边均包含了待求量Z,因此需采用迭代法来求解。方程(7)和(10)均使用牛顿迭代法,且均在满足Z的新量和旧量差的绝对值小于1×10-6的条件下求得近似解Z。
2 压缩因子实测值说明
本研究主要目标是对5个方法进行计算准确度评价,最好的评价方法就是将计算值同实测值进行对比。鉴于GB/T 17747.2-2011《天然气压缩因子的计算—第2部分:用摩尔组成进行计算》已对AGA8-92DC方法的使用范围及相应不确定度有了明确的说明,即对给定组成范围内的管输气,当温度低于263 K,压力最高至10 MPa,计算结果的不确定度保持在0.1%内;当温度为263~350 K,压力最高至12 MPa,计算结果的不确定度为0.1%;当温度高于290 K,压力最高为30 MPa,计算结果的不确定度也为0.1%。因此,本研究特把低中压的酸性贫气作为压缩因子计算对象,其在气体组成范围内和压力范围内都超出了GB/T 17747.2-2011关于AGA8-92DC方法的不确定度评定范围。
在对比评价过程中,使用了113个贫气压缩因子实测值,其中包含66个含碳贫气数据,47个含硫含碳贫气数据。含碳贫气压缩因子数据来源于Thomas等[10]的实验,实验温度和压力变化范围分别为310.93~344.26 K和7.07~48.44 MPa。该实验所用设备由高压系统和低压系统两部分组成,其中高压部分包括可变容积单元、水银泵和恒温单元,其作用为根据状态方程求得压缩因子;而低压部分包括色谱分析仪,其作用为测得气样摩尔组分。含硫含碳贫气压缩因子数据来源于黄德明等[11]对PX井的气样参数实测,其实测温度为333.15 K,压力为9~55.17 MPa。以上各气体样本的具体摩尔组成见表2,其中气样1~气样3为含碳贫气,气样4为含硫含碳贫气。
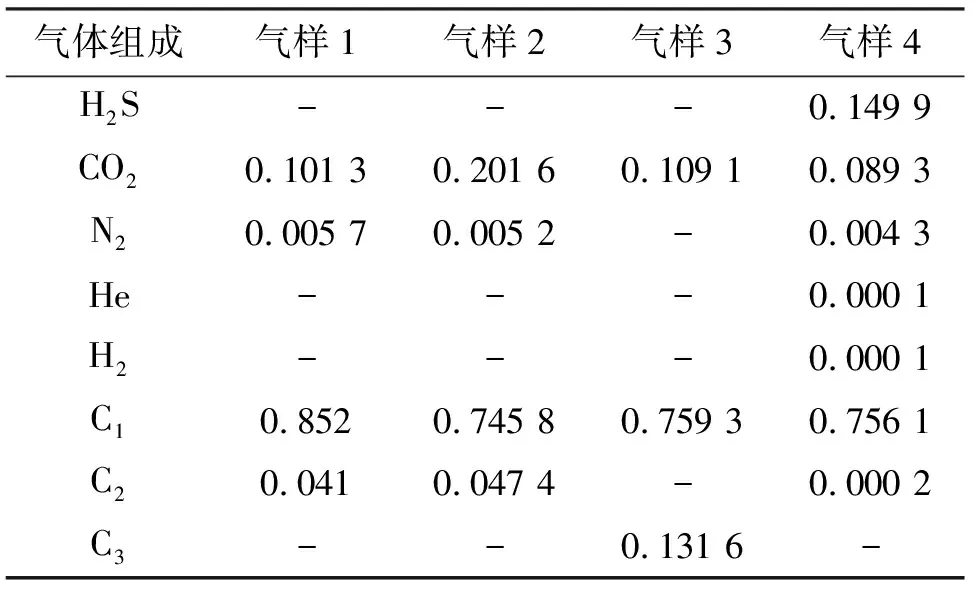
表2 气体组成数据(摩尔分数)
3 计算结果分析
该部分是对5个求解压缩因子的方程进行计算准确度评价。通过已知气体组成和给定的温度及压力条件,对比5个方程的计算值与实测值,从而找出在一定条件下求解压缩因子准确度最高的方程。
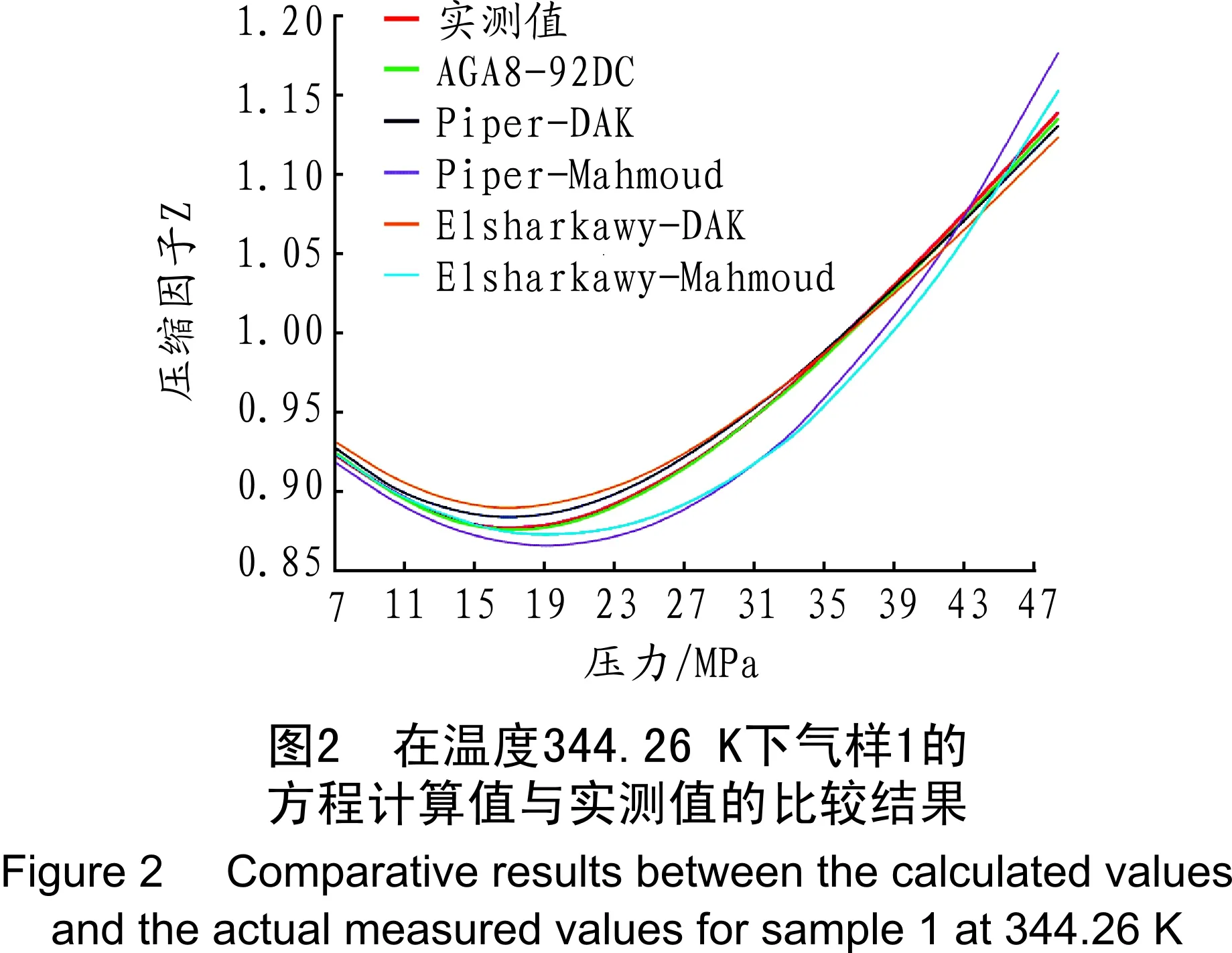
首先采用3组(66个实测压缩因子数据)低中压含碳贫气作为测试对象,其气体组成见表2中气样1~气样3。对于每组气样,其测试条件为:温度310.93 K和344.26 K,压力变化为7.07~48.44 MPa,3组气样中所涉及的对比温度、对比压力范围为1.428≤Tr≤1.766、1.394≤pr≤9.985。对于气样1,当T=310.93 K时,5个方程压缩因子计算值与实测值的比较结果见图1,其中11个压缩因子实测值与方程计算值的结果见表3;当T=344.26 K时,5个方程的计算值与实测值的比较结果见图2。经观察对比可知,AGA8-92DC、Piper-DAK与Elsharkawy-DAK方程的计算值在给定压力范围内始终与实测值保持较小的误差。另外,当温度变为344.26 K时,5个方程的计算值误差均在一定程度上有所减小。5个方程关于气样1~气样3在两种温度条件下和相同压力范围内的计算值平均相对误差见表4。由表4可知,当温度为310.93 K,AGA8-92DC方程的平均相对误差最小,其3组气样的平均相对误差为0.55%,而Piper-Mahmoud方程的平均相对误差最大,其3组气样的平均相对误差为3.97%;而当温度增加到344.26 K时,5个方程的平均相对误差均有所减小,此时,AGA8-92DC方程关于3组气样的平均相对误差仅为0.30%,Piper-Mahmoud方程关于3组气样的平均相对误差降为2.43%。
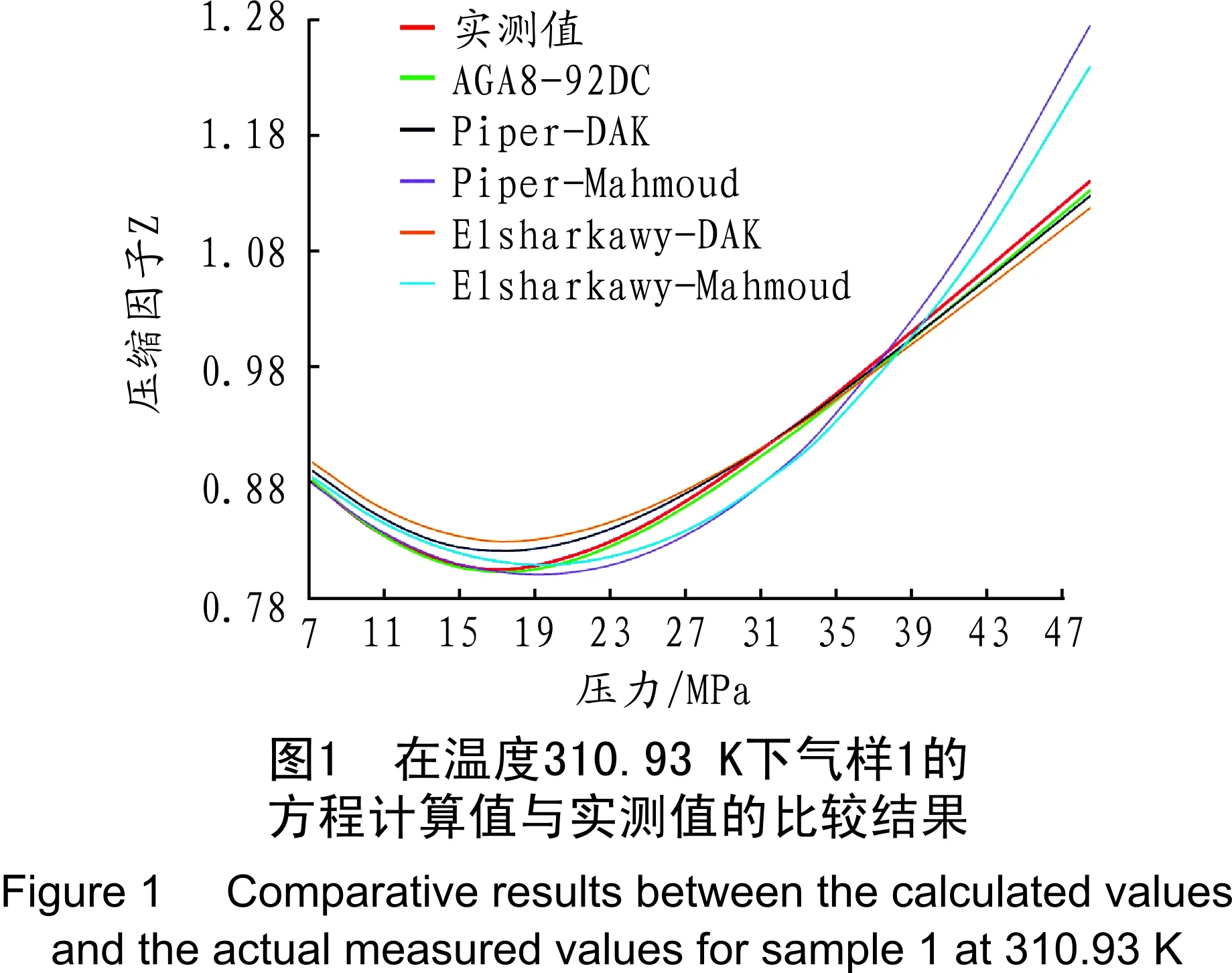
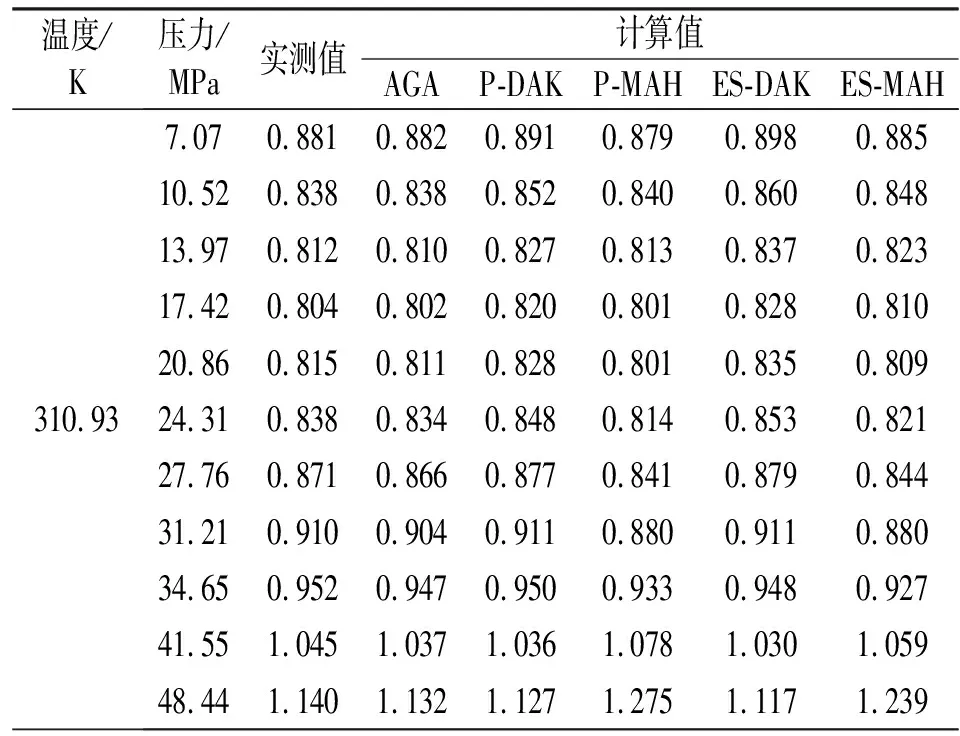
表3 气样1的压缩因子实测值与方程计算值结果
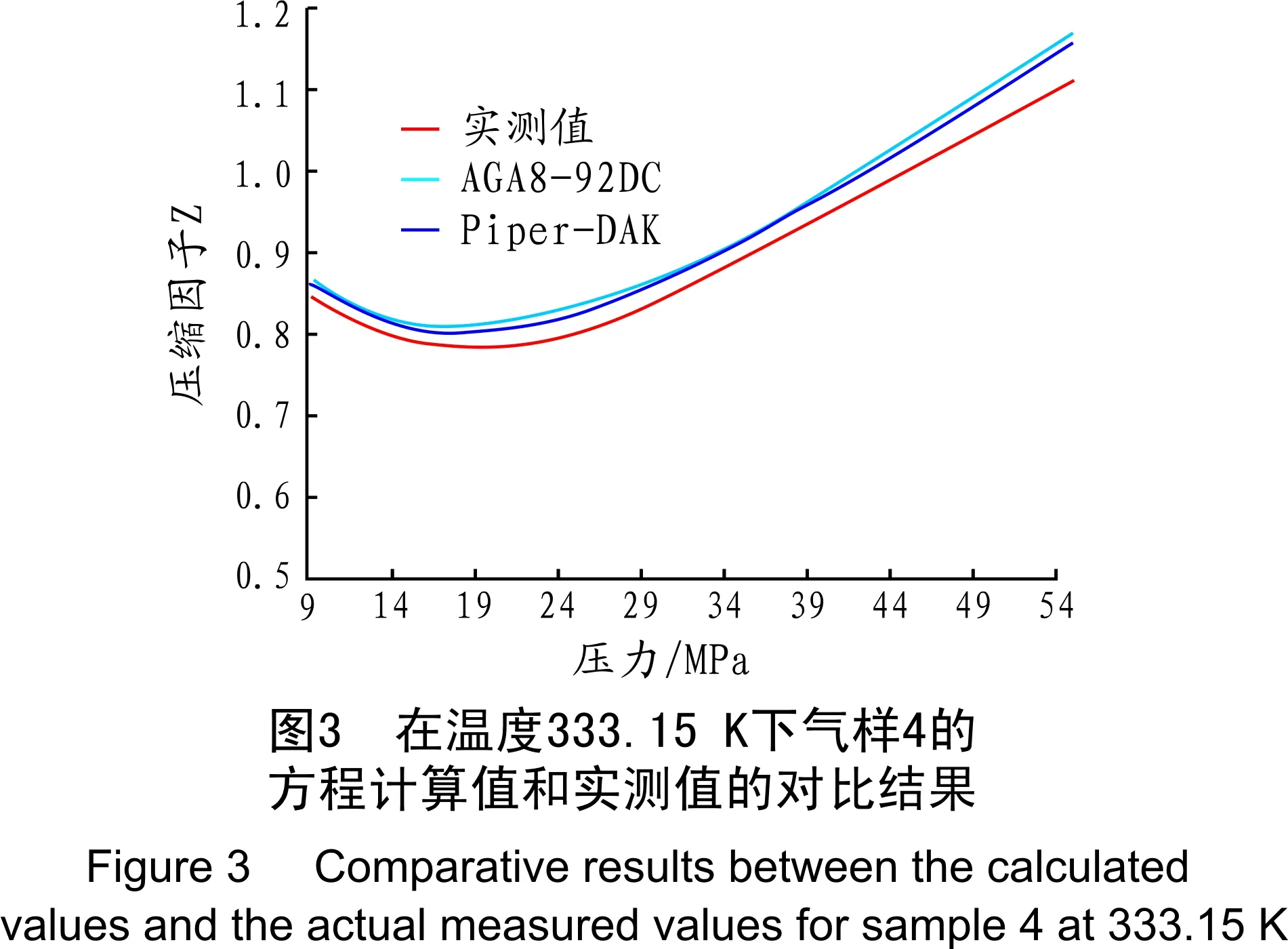
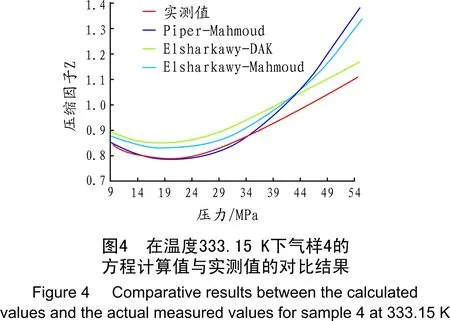
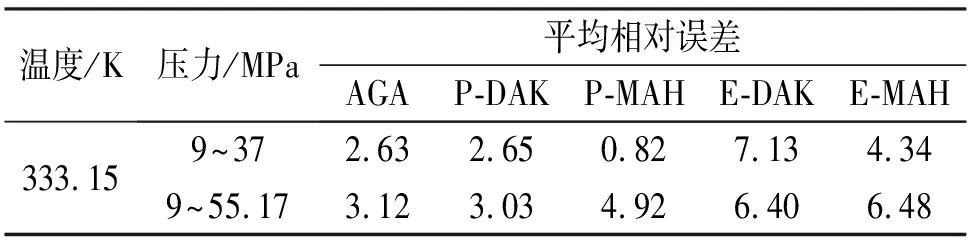
为了解5个方程对含硫含碳酸性贫气的使用准确度,将气样4作为测试对象,其组成见表2。图3和图4显示了5个方程的计算值与压缩因子的实测值的对比结果,其测试温度保持不变(T=333.15 K=599.67 °R),压力变化范围为9~55.17 MPa(1 305.36~8 001.85 psia),其相应的对比参数为Tr=1.565和1.713≤pr≤10.50。从图3可以看出,AGA8-92DC方程与Piper-DAK方程,在给定压力范围内始终与实测值保持较好的一致性,但两个方程的计算值均大于实测值。从图4可见,在37 MPa(pr=7.040)以前,Piper-Mahmoud方程的计算值与实测值基本重合,但在37 MPa以后,其计算值开始偏离实测值,且偏离程度随着压力的增大而不断变大。另外,Elsharkawy-DAK方程和Elsharkawy-Mahmoud方程的计算值始终与实测值保持一定的正偏差,但在42 MPa(pr=8.105)以后,Elsharkawy-Mahmoud方程的计算值偏离实测值的程度开始不断变大。表5直观显示了5个方程关于气样4的压缩因子计算值的平均相对误差。由此得到以下结论:对于低中压的含硫含碳贫气(pr≤7.040),采用Piper-Mahmoud方程计算气体压缩因子,其准确度较高,平均相对误差为0.82%;对于压力较高的含硫酸性贫气(7.040 表4 压力变化为7.07~48.44 MPa,方程计算值Z的平均相对误差(%) 表5 气样4的方程计算值Z的平均相对误差(%) 根据以上4组测试气样的组成和测试压力范围(7.07~55.17 MPa)可知,其评价结果主要适用于地下气藏。本研究结论如下: (1) 对于地面管输气,GB/T 17747.2—2011已明确了AGA8-92DC方法的应用范围和相应的不确定度。对于超出该标准不确定度评定范围的低中压含碳贫气(1.394≤pr≤9.985),AGA8-92DC方程的计算准确性依然较理想,其平均相对误差不超过1%。因此,对于低中压或开发后期的含碳贫气气藏,采用AGA8-92DC方程计算其气体压缩因子,能够满足地层储量预测及气田开发等相关工程计算的准确度要求。 (2) Piper的混合法则因考虑了气体中非碳氢组分的影响(如H2S、CO2等),避免了使用修正公式对伪临界参数的修正;Mahmoud方程形式简单且在求解压缩因子时无需迭代计算。另外,因GB/T 17747.2—2011中AGA8-92DC方程主要适用于管输气,而不涉及对含H2S气体的计算压缩因子的不确定度评定。因此,对于低中压的含硫含碳贫气(1.713≤pr≤7.040),使用Piper-Mahmoud方程求解压缩因子Z较其他方程来说误差最小,其平均相对误差小于1%。由此可见,对于低中压或开发后期的含硫含碳酸性贫气气藏,采用Piper-Mahmoud方程可以快速且较准确地求得气体压缩因子。 (3) 当天然气温度升高时,5个方程的计算值误差均会减小,但这并不会影响5个方程计算值的准确度优劣排名。 参考文献 [1] 李云清,何鹏,王金成.碳氢燃料在亚临界及超临界状态下的状态方程研究[J].石油与天然气化工,2007,36(1):1-3. [2] Adel M Elsharkawy, Yousef S kh S Hashem, Abbas A Alikhan. Compressibility factor for gas condensates[C]//Society of Petroleum Engineers, Midland, March 21-23, 2000. [3] Stewart W F, Burkhard S F, Voo D. Prediction of Pseudo Critical Parameters for Mixtures[C]//AICHE Meeting, Kansas City, 1959. [4] 熊钰,张烈辉,唐建荣.混合规则对天然气压缩因子预测精度的影响研究[J].石油与天然气化工,2004,33(6):447-449. [5] Piper L D, McCain Jr, Corredor J H. Compressibility Factors for Naturally Occurring Petroleum Gases[C]//Society of Petroleum Engineers, Houston, Oct 3-6,1993. [6] Dranchk P M, Abou-Kasem J H. Calculation of Z factors for natural gases using equations of state[J]. Cdn. Pet. Tech., 1975, July-Sept: 34-36. [7] Mahmoud M A. SPE, King Fahd University of Petroleum & Minerals, Development of a New Correlation of Gas Compressibility Factor (Z-Factor) for High Pressure Gas Reservoirs[C]//Society of Petroleum Engineers, Cairo, April 15-17,2013. [8] Shashi Menon E. Gas Pipeline Hydraulics[M]. Boca Raton: CRC Press from Taylor & Francis Group, 2005. [9] 全国天然气标准化技术委员会(SAC/TC 244).GB/T 17747.2-2011 天然气压缩因子的计算-第2部分:用摩尔组成进行计算[S].北京:中国标准出版社,2012. [10] Thomas S Buxton, John M Campbell. Compressibility factors for lean natural gas-carbon dioxide mixtures at high pressure[J]. SPE Journal, 1967,7(1):80-86. [11] 黄德明,付德奎,胡杰,等.高酸气田天然气偏差因子计算方法[J].天然气技术与经济,2012,6(6):30-33.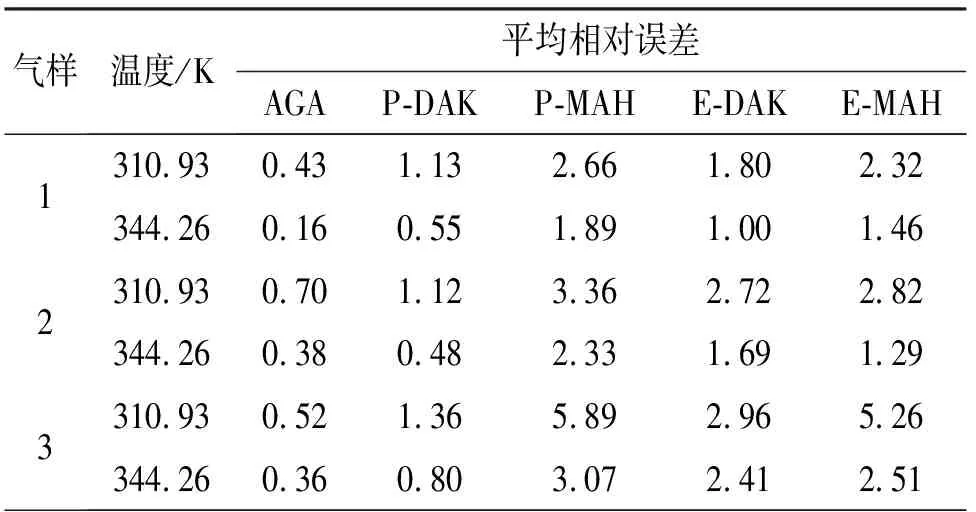
4 结 论

