BP神经网络与GA算法相结合的空调风叶翘曲均匀性优化

黄立东，周小蓉

（湖南机电职业技术学院机械工程系，湖南 长沙410151）

0 前言

空调中的风叶作为送风的主要装置，其性能的好坏直接关系到空调工作状况的好坏。风叶注塑时，由于各个叶片受到的压力可能不同，将使得各个叶片产生的翘曲不一致，这将直接决定着风叶叶片的品质，因此必须确保3个叶片翘曲的平衡性。

关于注塑产品的翘曲优化问题，许多学者都做过相关研究，Fei等[1]利用BP神经网络对产品进行了翘曲预测及优化；Gao等[2]利用Kriging代理模型减少了产品翘曲量；Erzurumlu等[3]采用正交实验、信噪比率和遗传算法得出了最小翘曲和缩痕指数的优化组合；Hakimian等[4]利用正交实验研究了微齿轮的翘曲和收缩性质；Deng等[5]利用MIPS方法及GA算法对产品翘曲量进行了优化。不过以上研究大多集中于对产品翘曲量最值的优化，而对于注塑产品而言，翘曲的整体均匀性甚至比翘曲量最值更重要，因此，简单的以翘曲量的最大值来衡量最终产品翘曲的好坏，具有一定的局限性。对于本文提出的空调风叶件，3个叶片的翘曲均匀性就对最终产品品质起着决定性作用。本文研究的空调风叶计算机辅助工程（CAE）模型如图1所示，未注塑时，其3个叶片叶尖处A、B、C 3点的坐标如图1所示。注塑后，由于空调风叶件发生翘曲变形，A、B、C 3点原本一致的Z轴坐标很难再保持一致，这说明了空3个叶片的翘曲并不均匀对称，而对于实际生产的空调风叶件，其叶尖处A、B、C 3点处的Z轴坐标必须处于一定的范围才能满足实际要求。因此，本文提出采用3个叶片叶尖A、B、C 3点Z轴坐标差值的最大值来衡量3个叶片的翘曲均匀性，并以工艺参数模具温度、熔体温度、注射时间、保压时间、保压压力为设计变量，A、B、C 3点Z轴坐标差值的最大值为目标变量，采用BP神经网络构建设计变量与目标变量之间的数学关系模型，并利用GA算法对数学模型进行全局最优求解，以提高产品最终的翘曲均匀性。

1 CAE模型建立

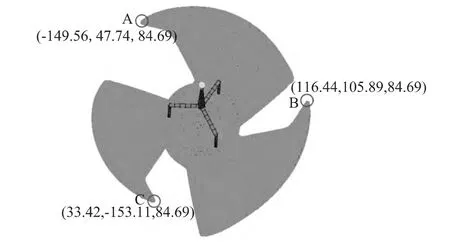
图1 有限元模型Fig.1 CAE Model

结合实际生产在Moldflow软件中构建如图1所示的有限元模型，其中网格为双面网格，其中网格匹配率为90.8%，通过非牛顿流动非等温条件下的广义Hele-shaw[6]流动控制方程控制熔融聚合物的充填。分析类型采用填充＋保压＋翘曲，材料为丙烯腈-苯乙烯共聚物（AS）＋20%玻璃纤维，工艺参数设置采取默认。得到填充时间为1.692 s，浇口冻结时间为11.59 s，速度/压力（V/P）转换时压力为55.62 MPa，如图2所示。根据经验，保压压力一般为V/P转换压力的60%～120%，保压时间为不能大于浇口冻结时间减去注射时间，因此保压压力为33～67 MPa左右，保压时间不能大于9.9 s。

根据CAE默认分析，得到注射位置处的注射压力变化如图3所示，由图3可以看出，注射位置处的最大压力为55 MPa左右，注射位置处的压力随时间呈均匀变化趋势，这说明了在填充过程中整个产品上的压力梯度是均匀的，说明了充填平衡及充填效果良好。

图2 默认工艺参数CAE模拟结果Fig.2 CAE analysisresults under the default parameters

2 田口实验设计及CAE模拟

选取四水平五因素进行田口实验设计，表头选用L16（45），根据材料属性，模具温度范围为40～80℃，熔体温度范围为200～270℃，结合CAE默认分析得到的注射时间、保压压力及保压时间范围，确定各因素及水平的设置如表1所示。

根据田口实验设计方案进行CAE模拟，得到正交矩阵及模拟结果如表2所示。

3 BP神经网络构建

BP神经网络具有强大的时变性、非线性逼近能力，大量文献[7-11]都有过关于BP神经网络的介绍，笔者在此就不再介绍。笔者在表2中随机选取11组数据对神经网络进行训练，用剩余的5组数据进行验证。采用mapminmax函数对数据进行归一化处理，训练后的网络结构为5-16-1，隐含层采用logsig传递函数，输出层为purelin线性函数，采用traingd函数进行训练。得到训练均方差随着迭代的变化如图4、5所示。从图4可以看出，经过2965次迭代后，误差减小到0.00001，迭代结束，BP神经网络构建完成。图4为构建的BP神经网络预测值与CAE模拟值对比图，可以看出，构建的BP神经网络预测值与实际值达到了很好的吻合。这说明构建的BP网络能够很好的反映目标函数与设计变量的之间的函数关系。

图3 注射位置处压力Fig.3 Pressure atinjection location

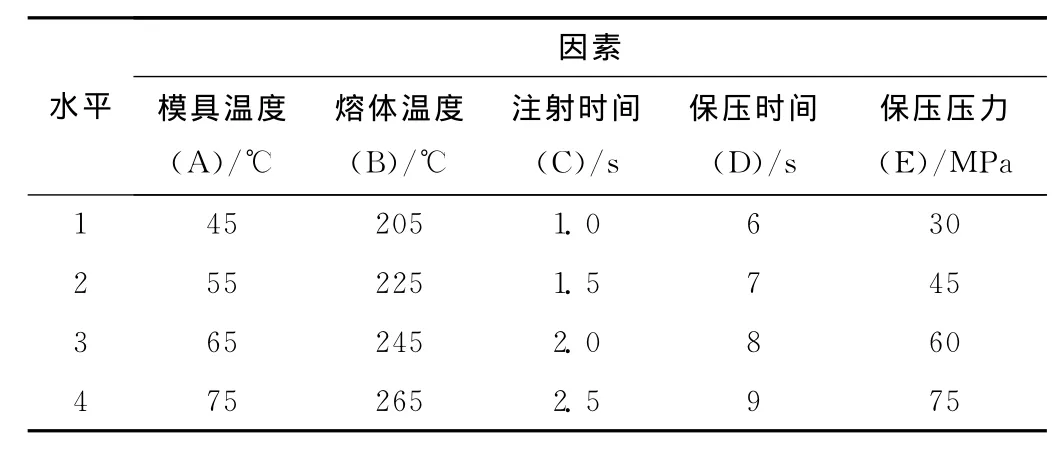
表1 因素与水平设置Tab.1 Factors and level set

表2 实验正交矩阵及模拟结果Tab.2 Experiments of orthogonal matrix and simulationresults

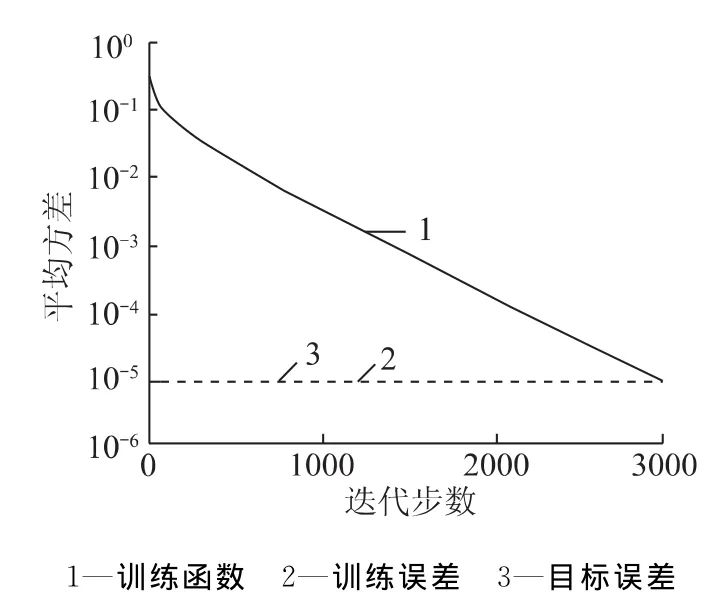
图4 训练误差Fig.4 Trainning error

图5 BP神经网络预测误差Fig.5 BP network prediction error

4 遗传算法工艺寻优

遗传算法是模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法，大量文献[12-16]对遗传算法都有过介绍。笔者基于上述构建的BP网络模型，采用实数编码遗传算法求解上述约束非线性最小值问题。种群大小为20，交叉概率为0.4，变异概率为0.2，经过100次迭代得到目标函数最优值为0.0445，小于所有训练和测试样本的值。遗传算法优化进程如图6所示，当经过50次迭代左右，适应度就达到最优值0.0445。得到最优工艺参数组合为：模具温度45℃、熔体温度205℃、注射时间1.8 s、保压时间6 s、保压压力50 MPa。

5 结果验证

根据得到的优化工艺参数，得到优化前后空调风叶整体翘曲情况对比如图7所示。其中图（a）表示优化前的风叶整体翘曲情况，Z轴的最大翘曲量为0.746 mm，图7（b）为优化后的整体翘曲情况，Z轴的最大翘曲量为0.396 mm。通过对比可以看出，优化后的风叶不仅最大翘曲量由0.746 mm降为了0.396 mm，而且风叶的整体翘曲也更加均匀。

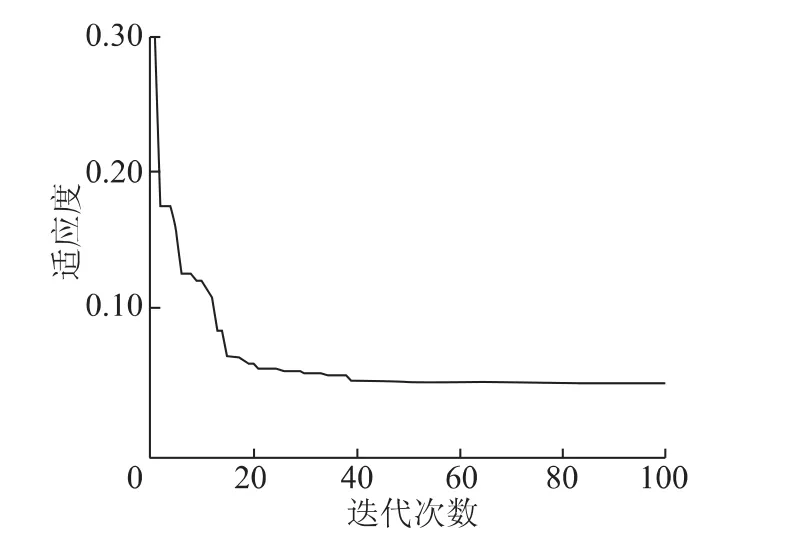
图6 适应度曲线Fig.6 Fitness curve

图7 优化前后风叶翘曲对比Fig.7 Blade warp contrast before and after optimization

图8 实际生产验证Fig.8 Actual production verification

根据优化后的工艺参数进行实际生产验证，得到实际生产的空调风叶如图8所示，其中图（a）为生产的空调风叶件产品，图（b）为机械手自动取件的空调风叶件注塑生产，图8（c）为生产的风叶件3个叶片尖部A、B、C 3点处的Z轴测量检测，经抽样检测，实际生产的空调风叶件满足公司内部标准，并且3个叶片的翘曲均匀。这实际验证了BP神经网络与遗传算法相结合优化工艺参数解决产品翘曲均匀性的可行性。

6 结论

（1）以打点风叶叶片尖部Z轴坐标最大差值来衡量风叶各叶片的翘曲均匀性是可行的；

（2）通过BP神经网络与遗传算法相结合的方法能很好的进行工艺参数优化以改善风叶的翘曲均匀性。

[1]Fei Yin，Huajia Mao.Back Propagation Neural Network Modeling for Warpage Prediction and Optimization of Plastic Products Duringinjection Molding[J].Materials and Design，2011，32：1844-1850.

[2]Yuehua Gao，Xicheng Wang.Surrogate-based Process Optimizing forreducing Warpageininjection Molding[J].Journal of Materials Processing Technology，2009，209：1302-1309.

[3]Erzurumlua T，B Ozcelik.Minimization of Warpage and Sinkindexininjection-molded Thermoplastic Parts Using Taguchi Optimization Method[J].Materials and Design，2006，27：853-861.

[4]Hakimian E，A B Sulong.Analysis of Warpage and Shrinkage Properties ofinjection-molded Micro Gears Polymer Composites Using Numerical Simulations Assisted by the Taguchi Method[J].Materials and Design，2012，42：62-71.

[5]Yimin Deng，Yong Zhang.A Hybr id of Mode-pursuing Sampling Method and Genetic Algorithm for Minimization ofinjection Molding Warpage[J].Materials and Design，2010，31：2118-2123.

[6]Kim S W，L S Turng.Developments of Three-dimensional Computer-a ided Engineering Simulation forinjection Moulding[J].Modelling and Simulationin Materials and Engineering，2004，12：151-173.

[7]Sadeghi B H M.A BP-neural predictor model for Plasticinjection Molding Process[J].Journal of Materials Processing Technology，2000，103（3）：411-416.

[8]Chow T T，G Q Zhang，Z Lin，et al.Global Optimization of Absorption Chiller System by Genetic Algorithm and Neural Network[J].Energy Build，2002，34（1）：103-109.

[9]Cheng J，Li Q S A hybr id Artificial Neural Network Method with Uniform Design for Structural Opitimization[J].Comput.Mech，2009，44（1）：61-71.

[10]Ozcelik B，T Erzurumlu.Comparison of the Warpage Optimizationin the Plasticinjection Molding Using ANOVA，Neural Network Model and Genetic Algorithm[J].Journal of Materials Processing Technology，2006，171（3）：437-445.

[11]史 峰，王小川.Matlab神经网络30个案例分析[M].北京：北京航空航天大学出版社，2010：1-45.

[12]Cook D F，C Tragsdale.Combining a neural Network with a Genetic Algorithm for Process Parameter Optimization[J].Engineering Applications of Artificialintelligence，2000，13（4）：391-39.

[13]Zhou J，A.Kramschuster.Single and Multiobjective Optimization forinjection Molding Using Numerical Simulation with Surrogate Models and Genetic Algorithm[J].International Polymer Processing，2006，21（5）：509-520.

[14]Kurtaran H，T Erzurumlu.Efficient Warpage Optimization of Thin Shell Plastic Parts Usingresponse Surface Methodology and Genetic Algorithm[J].International Journal of Advanced Manufaturing Technology，2006，27（5/6）：468-472.

[15]Shen Changyu，Wang Lixia，Li Qian.Optimization ofinjection Molding Process Parameters Using Combination of Artificial Neural Network and Genetic Algorithm Method[J].Journal of Materials Processing Technology，2007，183：412-418.