基于节点相似度的社团发现算法

程泽凯，张佳玉

（安徽工业大学 计算机学院，安徽 马鞍山243032）

0 引 言

社会网络是指社会个体成员之间因为互动而形成的相对稳定的关系体系，这些个体成员拥有共同的兴趣、同属某一特定的主题或是共有某种属性［1］。随着社会关系网络中关系数据的日益丰富，对关系数据的链接挖掘也成为各大研究者的热门课题。社会网络挖掘中，社会网络可形式化描述为社会关系网络图，通过聚类方法将其划分为不同的子图，即抽取出其中隐含的子模式，就是节点聚类［2］，也就是社团发现。研究发现，社团结构是社会网络具有的一个共同性质，满足同一社团内部节点连接相对紧密、不同社团间节点连接相对稀疏的特点。社团内部成员具有很大的相似性，研究社团结构对于了解网络结构与分析网络特性，充分利用网络价值都很重要。

社会网络中除了存在拓扑结构信息外，还存在丰富的节点属性信息，如何充分利用各方面的信息有效地发现社团结构成为社团发现中的基本问题，这种有效性体现在两个方面：如何充分利用拓扑结构及节点属性提高算法的准确率和如何提高算法的执行效率。

1 社会网络社团发现

通过对现有的社会网络社团发现算法进行分析研究，我们将其分为两类：基于优化的图聚类算法和基于启发式的图聚类算法［3］。第一类基于优化的图聚类算法通过设定聚类目标函数提出试探性的算法来获取近似的社团结构。典型的有基于Laplace图特征值的谱平分法［4］和在GN算法基础上改进的基于modularity极值近似的 MEA算法［5］等等。该类算法并不能保证一个较高的Q值对应的就是较优的社团结构，算法准确率较低。第二类基于启发式的图聚类算法通过设计符合现实意义的启发式规则来识别社团结构。典型的有基于马尔可夫随机游走模型的启发式符号网络聚类算法 （FEC）［6］和能够识别重叠网络簇的派系过滤算法 （CPM）［7］等等。该 类算法一般都具有较高的时 间复杂度。

以上两大类都是图分割算法，此类算法只依赖图的拓扑结构，这样不充分的划分条件导致社团划分准确率低。具有相似属性的节点之间更可能产生链接关系，在合著网络中，一个组织内的成员不仅存在着合著关系 （关系数据），同时也具有较为相似的研究兴趣 （属性数据）［8］。为了得到更优化的社团结构，研究者提出了解决图聚类问题的新思路。程鸿等人提出一种统一随机游走距离测量相似度的基于结构和属性的SA－cluster图聚类算法［9］；徐晓伟等人提出一种基于结构情境相似性的思想来计算网络中节点相似度的SCAN算法［10］；林友芳等人设计和实现了一种将个体和链接属性有效融合的社区发现算法CIG＿ESC［11］。

本文在分析现有算法的基础上，针对算法只考虑图的拓扑结构而忽略节点属性影响及算法的时间复杂度高的问题，提出了一种基于节点相似度的社团发现算法，遵循图聚类问题的另一种解决思路，即先综合结构和属性的影响求出节点相似度，然后使用传统的空间聚类方法进行聚类。本算法结合SA－cluster算法中构建属性扩展图的思想，将属性的影响加入拓扑结构图中，然后使用SCAN算法中结构化相似度的计算方法求得属性扩展图中节点的相似度，最后设计一种基于节点相似度的k－means聚类算法来发现社会网络图中的社团结构。本算法在多个基准网络数据集上的测试结果均验证了算法在准确率和时间复杂度上的有效性。

2 基于节点相似度的社团发现算法

2.1 基本概念

2.1.1 属性扩展图

社会网络的原始拓扑结构图G＝（V，E，M）由图中的节点集V、节点之间的边集E和与节点关联的m个属性值的集合M ＝ ｛a1，.....，am｝组成，定义节点集V中的节点为结构节点，个数为N，边集E中的边为结构边，用实线表示，原始图如图1所示。构造属性扩展图的步骤如下：将待考虑属性的m个取值作为m个属性节点加入原始图中，若某结构节点具有该属性，则在此结构节点和该属性节点之间添加一条属性边，用虚线表示。构造后的属性扩展图G′可表示为G′＝ （V′，E′，M），V′为 ∪Vi和 ∪Vai的集合，如图2所示。

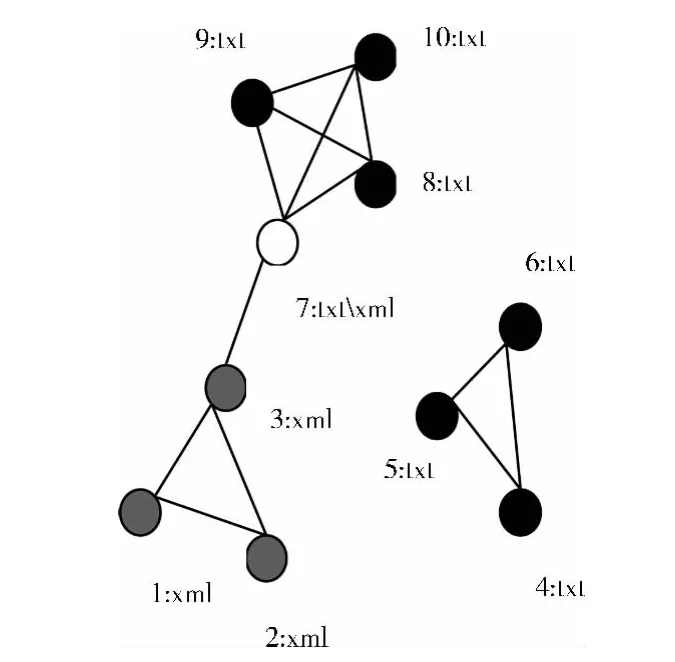
图1 原始图

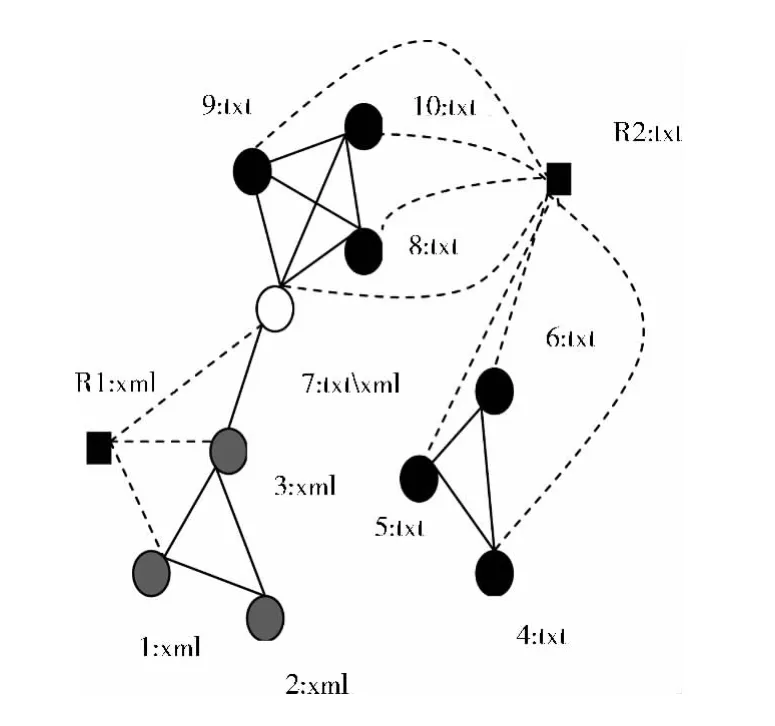
图2 属性扩展

图1原始图中含10个结构节点，图中标明的是节点的类别属性，含两个值txt和xml，构造属性扩展图时，在原始图中添加属性节点R1：xml和R2：txt，并且在含该属性的结构节点和该属性节点之间添加属性边，从图2中可以发现，属性边的加入使得属性相同的节点之间连接更加紧密。

2.1.2 基于结构情境的相似度

基于结构情境相似性的思想来源于以下规则：在社会网络中如果两个节点有相似的近邻，则这两节点就是相似的，即在现实的社会网络中，两个从共同朋友那里接受推荐的人常常做出相似的决策。

定义 给定无向图G＝（V，E，M），对于节点u∈V，u的领域定义为

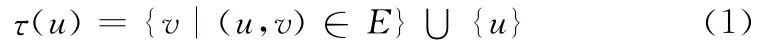
使用情境化相似度的思想，用规范化的公共邻域大小来度量两节点u，v之间的相似性，该值越大，两节点相似度越高。结构化相似度定义如下

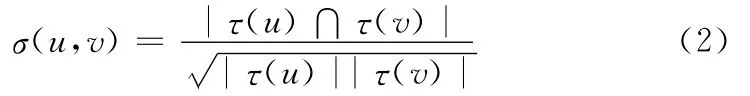
上述定义是针对相邻节点的，对于非相邻节点，这种局部性定义不能正确表达节点间的距离，这里我们定义非相邻节点间的结构化相似度由最短路径上相邻节点对的结构相似度的乘积的最大值来表达。其中，最短路径使用广度优先遍历方法得到

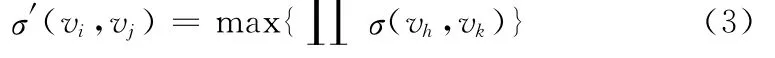
式中：vi、vj——图中的 非 相 邻 节 点，vh、vk——vi、vj的 最短路径上的相邻节点对。

2.1.3 社团模块度

社团模块度用于衡量整个网络的划分质量。假设网络划分为k个社团，定义k阶矩阵E＝（eij）k＊k，eij表示网络中连接两不同社团i和j的节点的边在所有边中所占的比例。模块度Q值定义为

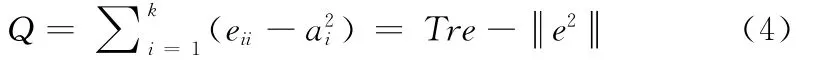
式中：Tre＝∑eii为E对角线上元素之和，表示网络中连接某一社团内部各节点的边在所有边中所占的比例；ai＝∑eij是每行中个元素之和，表示第i个社团中的节点与其它节点相连的边在所有边中所占的比例。模块度Q值越大说明社团结构越明显。

2.2 社团发现算法SASK

2.2.1 算法描述

给定无向图G＝ （V，E，M），V 中节点总数为 N，M ＝｛a1，.....，am｝，其中ai（i＝1，.....，m）是节点关联属性的m个取值，在原始图G中加入属性节点和属性边构造属性扩展图，针对属性扩展图G′＝ （V′，E′，M）使用基于结构情境的相似度计算方法计算每个结构节点的结构相似度，属性边的加入会使得具有同一属性的节点之间的相似度增大，对于每个属性节点，计算其到所有与之相连的结构节点的转移概率，并将此转移概率与节点的结构相似度相结合计算出最终的节点相似度，最后使用改进的k－means聚类算法在节点相似度的基础上对节点进行聚类，求得最终的社团结构，其中聚类初始中心点的选取遵循最大最小原则。该算法可简称为 SASK （K－means based on node similarity with structure and attributes）。

SASK算法流程描述如下：

输入：无向网络图G＝（V，E，M）；

输出：网络G的社团结构；

步骤1 如果V为空，算法结束；否则，读入原始图G＝（V，E，M），根据属性与节点的从属关系构造属性扩展图G′＝ （V′，E′，M），得到G′中节点的邻接矩阵；

步骤2 根据式 （1）～式 （3）计算得到属性扩展图G′中节点的结构相似度矩阵；

步骤3 当属性节点与其它节点相邻时，用属性节点的转移概率矩阵更新节点的结构相似度，得到节点相似度矩阵；

步骤4 使用改进的k－means算法对图G′中的节点聚类。根据最大最小原则确定K个初始聚类中心点，即首先选择度数最大的节点k1加入初始簇心core中，该类节点有较大的凝聚力，然后采用最小相似度原则将与已入簇节点的平均相似度S最小的节点作为新的初始聚类中心点加入初始簇心集合。其中，为了排除孤立点的影响，选取节点度数平均值作为候选簇心的筛选阈值；

步骤5 更新簇。将除初始聚类中心点以外的其它节点划分到相似度较高的簇心所在的簇中，确定此次迭代后得到的社团结构；

步骤6 更新簇心集合。计算节点在已划分好的社团内部的度数，将度数最大的节点作为新的簇心，得到新的簇心集合core。若新的簇心与上次迭代的簇心不同，则重复步骤5；若相同，则停止迭代，输出最终的社团结构。

2.2.2 算法时间复杂度分析

假设网络图中含n个节点，m条边。通过上述分析，节点结构化相似度的计算的时间复杂度取决于查询节点的度deg（vi），总 代 价 为 O（deg（v1）＋...＋ deg（vn）），相当于每条边都要被计算两次的次数，因此时间复杂度为O（m）；使用最大最小原则选取k个初始聚类中心点时，每选取一个要比较的次数为n，因此中心点确立的时间复杂度为O（kn）；n个节点往k个簇中归类时，需要比较的次数是kn，迭代次数是t，时间复杂度为O（nkt）。由此可得，算法总体上时间复杂度为线性复杂度O（（t＋1）kn＋m）。

3 实验结果分析

3.1 带属性的人工构造的二社团网络

如图3所示是由11个节点构成的作者合著关系图，两节点之间有边即代表两作者合著一篇论文，xml和skyline是作者所著论文文献类别属性的两个取值。

图4是加入两属性值后构造得到的属性扩展图。通过算法验证，属性扩展图的构造使得属性的影响增大了，属性相同的节点间的结构化相似度增加，用改进的k－means聚类算法作用于得到的节点相似度，迭代一次得到最终社团结构。其中，筛选阈值为度数平均值3。表1所示为去除算法第一步属性扩展图的构造得到的社团发现结果和SASK算法得到的结果，结果分析如下：

3.2 不带属性的数据集

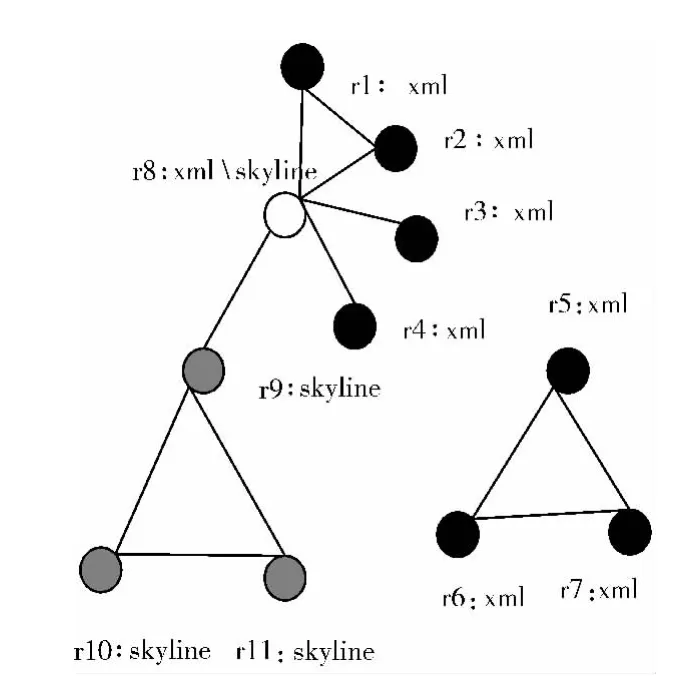
图3 作者合著关系

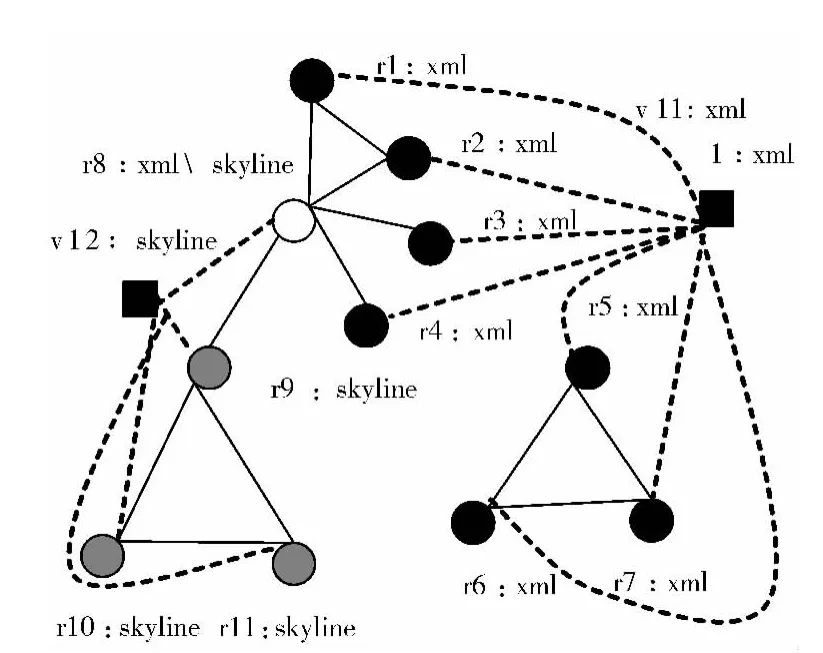
图4 图3的属性扩展

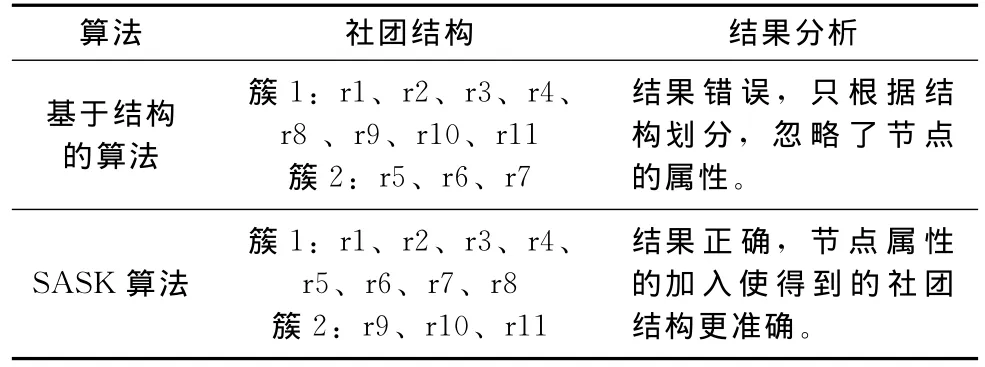
表1 基于结构的结果与本文算法的结果对比

为了进一步验证该算法的有效性和通用性，我们在将其在另外两个社会网络社团发现领域的基准数据集上进行测试，并将SASK算法的时间复杂度、准确率等性能指标与一些经典算法在这些数据集上的测试结果进行对比。

3.2.1 Zachary’s Club空手道俱乐部网络

Zachary空手道俱乐部网络是 Wayne Zachary构造的美国空手道俱乐部成员关系网，如图5所示，网络由34个节点、78条边组成，节点表示俱乐部成员，边表示成员之间存在关系。该俱乐部就是否抬高俱乐部收费问题产生分歧，分成了以主管和校长为中心的两个小社团。作为验证社团发现算法的基准网络，“Zachary空手道俱乐部网络”常用于测试算法能否根据观察到的网络结构预测出最终的分裂情况。

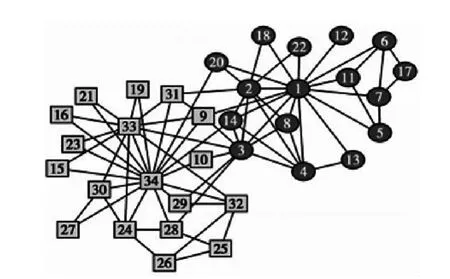
图5 Zachary空手道俱乐部网络

根据上述算法步骤计算出节点相似度，使用最大最小原则选取两个初始簇心，将最大度节点34（度数为17）作为第一个中心点加入簇心，在个节点度数大于筛选阈值为度数平均值5的条件下，节点1与节点34之间的有最小相似度0.11，根据最小相似度原则将节点1加入初始簇心；使用k－means算法迭代一次得到最终的社团结构。结果如图5所示，是以节点1为中心的圆形标记的社团和以节点34为中心的方形标记的社团。事实上，节点1和节点34表示俱乐部的主管和校长。SASK算法与其它经典算法在该数据集上的准确率及时间复杂度对比见表2。

表2 Zachary空手道俱乐部网络准确率对比

表2的对比结果验证了算法在该数据集上的有效性。

3.2.2 American College Football美国大学足球网络

美国大学足球网络是由Girvan和Newman针对美国大学生足球联赛抽取出的社会网络模型，其中，每个节点代表一个足球队，节点间的边表示两球队进行过比赛，该网络含115个节点和616条边。按地理位置划分，球队可分为12个联盟，根据规定，联盟内的球队比赛的次数比不同联盟的球队多。该网络是验证社团发现算法的另一个常用基准网络，但是网络中含有一些噪声节点，噪声节点的存在会影响社团识别的准确率。

根据上述算法步骤，该数据集上最终得到的12个社团结构见表3。其中，上行是该网络的实际社团结构，下行是SASK算法得到的社团结构，社团划分的准确率根据正确划分到该社团中的节点在正确社团节点中所占的比例来计算。

SASK算法识别出的社团结构与实际社团相比，有11个节点识别错误。由于孤立点及最大最小原则选取初始簇心时筛选阈值的设置的影响，其中一个簇心选择错误，使得该簇中的节点被错误地分到其它簇中；其余的节点均能被识别出来，基本上与真实社团结构相符合，划分的社团的准确率整体上可达86.7%，经典的Newman快速算法在该数据集上的准确率为78%；赵凤霞提出的k－means复杂网络社团发现算法［12］在该数据集上的准确率为83%。

表3 SASK算法对美国大学足球网络社团发现的结果

SASK算法共迭代6次，通过模块度计算发现，迭代总体上向着模块度增加的方向，表明迭代使得社团结构越来越明显。每次迭代的模块度Q值及变化趋势如图6所示。SASK算法发现的社团模块度Q值为0.585，Newman快速算法中得到的最优模块度Q值为0.546。

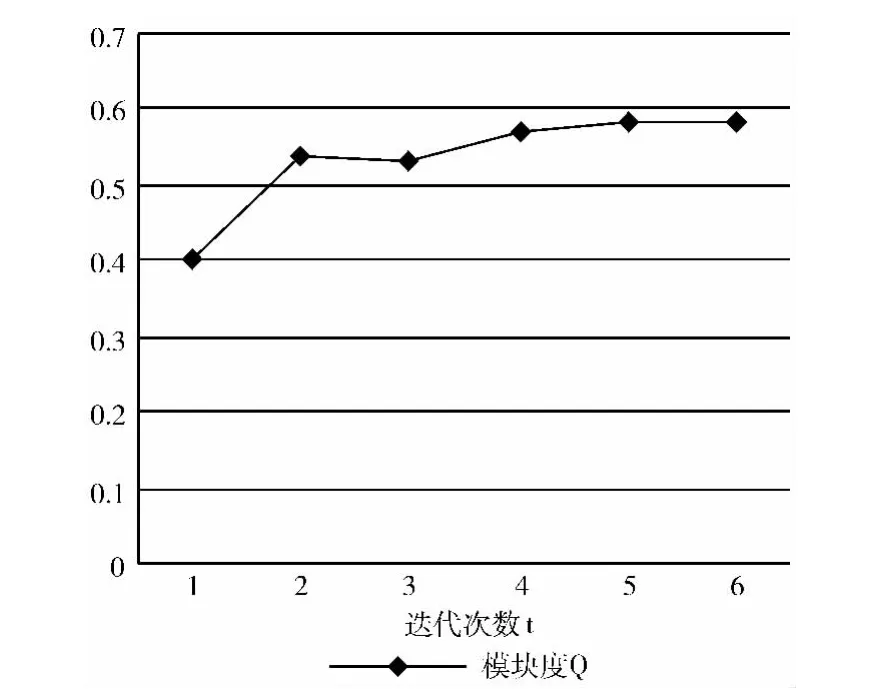
图6 模块度Q值随迭代次数的变化趋势

4 结束语

本文创新点在于综合了结构和属性的因素，结合属性扩展图和结构化相似度的思想，提出了一种基于节点相似度的社团发现算法SASK，将图聚类问题转化为基于节点相似度的k－means空间聚类问题。与现有的社团发现算法相比，该算法发现的社团结构准确度更高，且时间复杂度是线性的。该算法在多个数据集上的测试结果均验证了算法的有效性。图节点间的链接关系也蕴含着丰富的信息，可用来衡量关系的强度，在未来研究中，可以将链接关系构造成边权值，与图拓扑结构和节点属性融合起来处理社团发现问题。

［1］Han J，Kamber M，Pei J.Data mining：Concepts and techniques ［M］.3rd ed.San Francisco：Morgan Kaufmann Publishers，2011.

［2］Tan PN，Steinbach M，Kumar V.Introduction to data mining［M］.Beijing：Posts and Telecom Press，2011.

［3］YANG Bo，LIU Dayou，LIU Jiming.Complex network clustering algorithms ［J］.Journal of Software，2009，20 （1）：54－66 （in Chinese）.［杨博，刘大有，Liu Jiming.复杂网络聚类方法 ［J］.软件学报，2009，20 （1）：54－66.］

［4］Shiga M，Takigawa I，Mamitsuka H.A spectral clustering approach to optimally combining numerical vectors with a modular network ［C］／／NewYork：Proc of the 13th ACM SIGKDD Int’l Conf on Knowledge Discovery and Data Mining，2007：647－656.

［5］ZHU Xiaohu，SONG Wenjun，WANG Chongjun，et al.Improved algorithm based on Girvan－Newman algorithm for community detection ［J］.Computer Science and Technology，2010，4（12）：1101－1108. ［朱小虎，宋文军，王崇骏，等.用于社团发现的Girvan－Newman改进算法 ［J］.计算机科学与探索，2010，4 （12）：1101－1108.］

［6］Yang B，Cheung W K，Liu J.Community mining from signed social networks ［J］.EEE Trans on Knowledge and Data Engineering，2007，19 （10）：1333－1348.

［7］Palla G，Farkas I J.Directed network modules ［J］.New Journal of Physics，2007，9 （6）：186－207.

［8］Ester M，Ge R，Gao B J，et al.Joint cluster analysis of attribute data and relationship data：The connected k－center problem ［J］.ACM Trans Know Discov，2008，2 （2）：1－35.

［9］Zhou Y，Cheng H，Yu J X.Graph Clustering Based on Structural／Attribute Similarities ［C］／／Proceedings of the 35th International Conference on Very Large Data Bases，2009：718－729.

［10］Xu X，Yuruk N，Feng Z，et al.SCAN：A structural clustering algorithm for networks ［C］／／CA，San Jose：Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，2007：824－833.

［11］LIN Youfang，WANG Tianyu，TANG Rui，et al.An effective model and algorithm for community detection in social net－works ［J］.Journal of Computer Research and Development，2012，49 （2）：337－345 （in Chinese）.［林友芳，王天宇，唐锐，等.一种有效的社会网络社区发现模型和算法 ［J］.计算机研究与发展，2012，49 （2）：337－345.］

［12］ZHAO Fengxia，XIE Fuding.Detecting community in com－plex networks using K－means cluster algorithm ［J］.Application Research of Computer，2009，26 （6）：2401－2404 （in Chinese）.［赵凤霞，谢福鼎.基于K－means聚类算法的复杂网络社团发现新方法 ［J］.计算机应用研究，2009，26（6）：2401－2404.］