上层建筑在起吊冲击载荷作用下结构强度分析
程玉芹,罗广恩
(1.淮海工学院机械工程学院,江苏 连云港 222003;2.江苏科技大学船舶与海洋工程学院,江苏 镇江 212003)
上层建筑在起吊冲击载荷作用下结构强度分析
程玉芹1,罗广恩2
(1.淮海工学院机械工程学院,江苏 连云港 222003;2.江苏科技大学船舶与海洋工程学院,江苏 镇江 212003)
以10.5万t油船为例,根据电机启动特性,运用MD/Nastran软件瞬态分析方法,对上层建筑在起吊瞬间各种不同工况下的动态响应进行计算,并对上层建筑平稳吊装过程中的应力进行计算。通过对比这2个阶段的结构应力,检验目前使用的上层建筑吊装安全系数的可靠性。
上层建筑;起升冲击载荷; 安全系数; 瞬态分析
0 引言
上层建筑吊装强度的常规计算方法是参考有限元直接计算指南[1]来进行有限元建模和计算的,通常采用吊装前和吊装过程中2个阶段对上层建筑结构的应力与变形进行校核。吊装前,结构放置于平台胎架上,惯性载荷即为重力加速度;吊装过程中,考虑到起吊瞬间对结构的冲击作用,将惯性载荷取为原重力加速度的1.1或1.2倍来近似模拟等效的冲击载荷,计算时采用静力计算的方法。该方法操作简便,但准确性有待进一步研究。
在实际吊装过程中,起吊时刻上层建筑结构所受到的冲击载荷是一个瞬态的过程。吊点处的外载荷不是一个固定值,而是一个在很短的时间内由零增加到结构自重的变化值,计算在这样一种随时间变化的激励载荷下的结构响应,必须借助瞬态分析的方法。用于瞬态响应分析的数值方法有2种[2,3]:直接法和模态法。何成忠[4]、汤秀丽[5]、王贡献[6]、赵爽[7]等采用瞬态分析的方法各自对不同形式的起重机的动态特性进行了研究,为不同形式的起重机动载荷的修正提供了理论依据。
本文将参考上述学者在起重机方面的研究,以105 000 DWT油船为例,采用瞬态分析中的直接法,并考虑结构阻尼的影响,详细分析上层建筑吊装时,起升冲击载荷对上层建筑结构应力的影响;计算不同起吊加速持续时间和起升电机特性下,上层建筑结构应力的变化情况;寻找到一个合理的起吊加速持续时间和恒定吊装速度,并检验目前采用的安全系数的可靠性。
1 上层建筑基本资料及有限元模型
105 000 DWT油船上层建筑共有5层,自上而下分别为罗经甲板、驾驶甲板、C 甲板、B 甲板、A 甲板。该船上层建筑沿船长方向为18.0 m(Fr29-2 000 mm至Fr49),船宽方向为42.0 m(上层建筑左右舷围壁间距26.24 m),船深方向为13.9 m(罗经甲板 2.7 m、驾驶甲板 2.8 m、C甲板2.8 m、B 甲板2.8 m、A 甲板 2.8 m)。上层建筑各层甲板采用横骨架式,在右舷靠船中设楼梯通道,Fr29、Fr47分别设围壁板,Fr35、Fr38分别设壁板;肋距800 mm,纵骨间距820 mm;上层建筑结构全部采用普通碳素钢,船体重量为348.386 t,重心靠左舷。
利用MSC/Patran软件对105 000 DWT油船5层上层建筑船体结构建立有限元模型,如图1所示。依据文献[1],有限元网格尺寸沿船长方向每肋位2个单元,船宽方向每纵骨间距2个单元;有限元模型中的板材均为平面板,板材采用四节点四边形单元;横梁、纵骨、纵桁采用梁单元模拟。建模时采用分组技术,共有79个组(Groups)、44 848个节点(Nodes)、58 850个单元(Elements)。
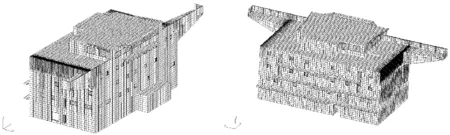
图1 105 000 DWT油船上层建筑整体结构有限元模型
通过定义全船结构有限元模型中构件单元的尺寸和密度,可以由程序自动计算船体结构构件钢材自重。居装件的重量主要是甲板敷料的重量,居装重量以分布力的形式施加到驾驶甲板、C甲板、B 甲板、A 甲板4层甲板上;其余重量相对较小,以密度的形式均匀施加于结构。调整结构的重量重心,使其与实际结构的重量重心相一致。
有限元模拟过程中的材料模型选择线弹性模型,密度7 850 kg/m3,弹性模量E=2.1×105MPa,泊松比v=0.3。
2 起吊瞬间不同工况下上层建筑结构应力分析
在上层建筑由静止到额定工作速度整个起升过程中的加速度主要取决于起升电机启动加速度特性。根据起升瞬态过程中的加速度变化曲线,可以得到上层建筑起升瞬态过程中的速度变化曲线。因此,起升电机的加速度曲线是决定上层建筑吊装起升瞬态过程中冲击载荷的关键因素。目前,龙门吊所采用的起升电机大都为变频电机,其调速性能良好,加速度特性曲线可以调成任意形式的特征曲线。变频电机的加速度特性曲线[1]有4种:半正弦(half-sine)加速曲线;正矢(versed-sine)加速曲线;梯形(trapezoidal)加速曲线;三角形(triangular)加速曲线,如图2所示。图2中,a(t)为变频电机的加速度,是一个随起吊加速持续时间τ变化的量;A为加速度幅值;r和h对应着梯形起升加速度曲线中的两个时间节点。
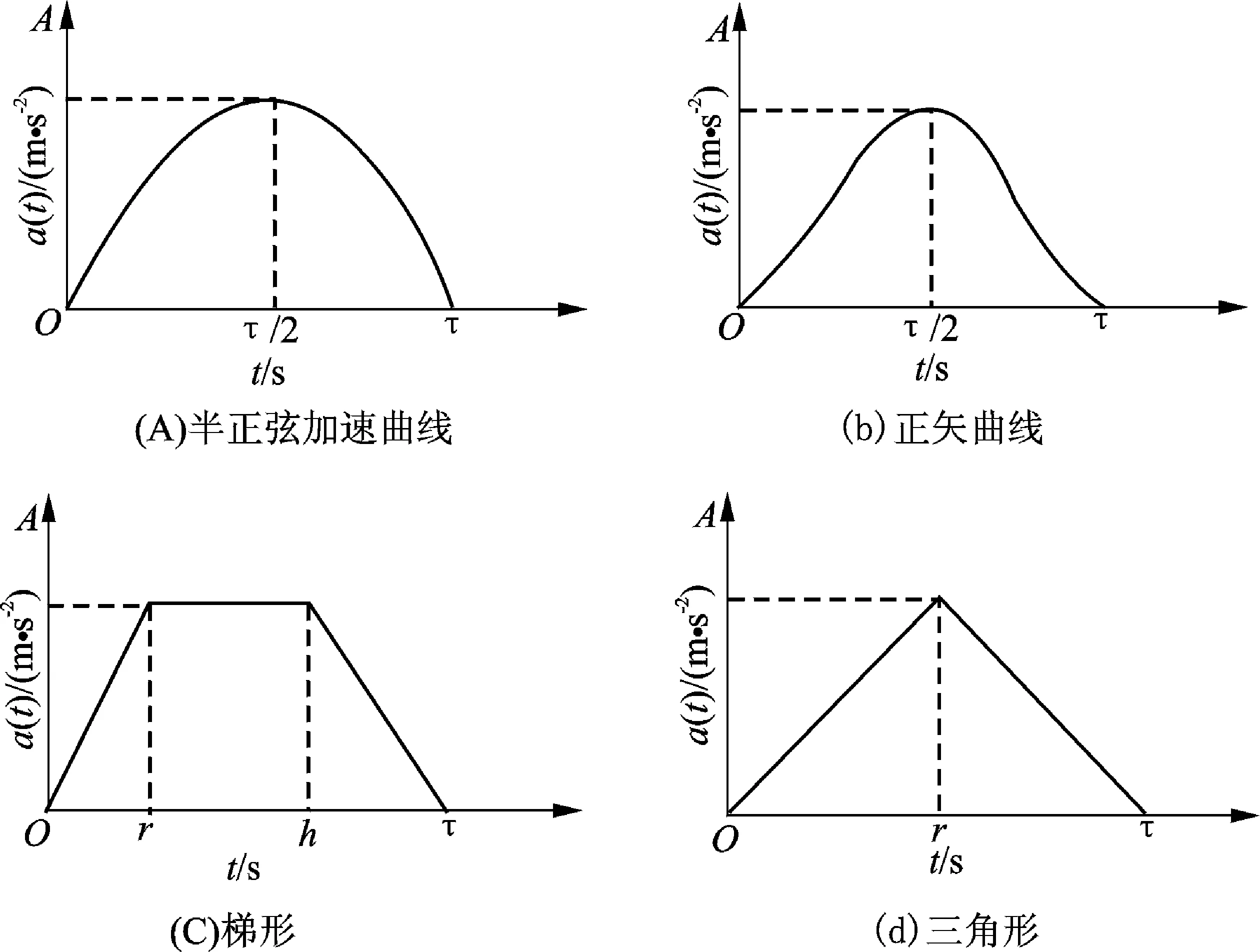
图2 4种起升加速度曲线
由于与加速度特性曲线相关的因素有起吊加速持续时间τ以及起吊瞬态过程结束时刻的恒定吊装速度v,因此本文分析不同的加速度特性曲线中τ和v的取值对起升冲击载荷下上层建筑结构应力的影响,通过对比分析得到一个合理的起吊加速持续时间和恒定吊装速度,并确定上层建筑吊装的安全系数。
对于起升电机采用半正弦加速曲线的情况,本文选择5种不同的起吊加速时间τ=1、1.5、2、2.5、3 s,结合4种不同的恒定吊装速度v=0.6、0.8、1、1.2 m/s共20种工况进行分析。对于后续的另外3种加速曲线,将同样采用此20种分析工况。为了便于区分,将工况前面加上不同加速曲线的首字母缩写,见表1。
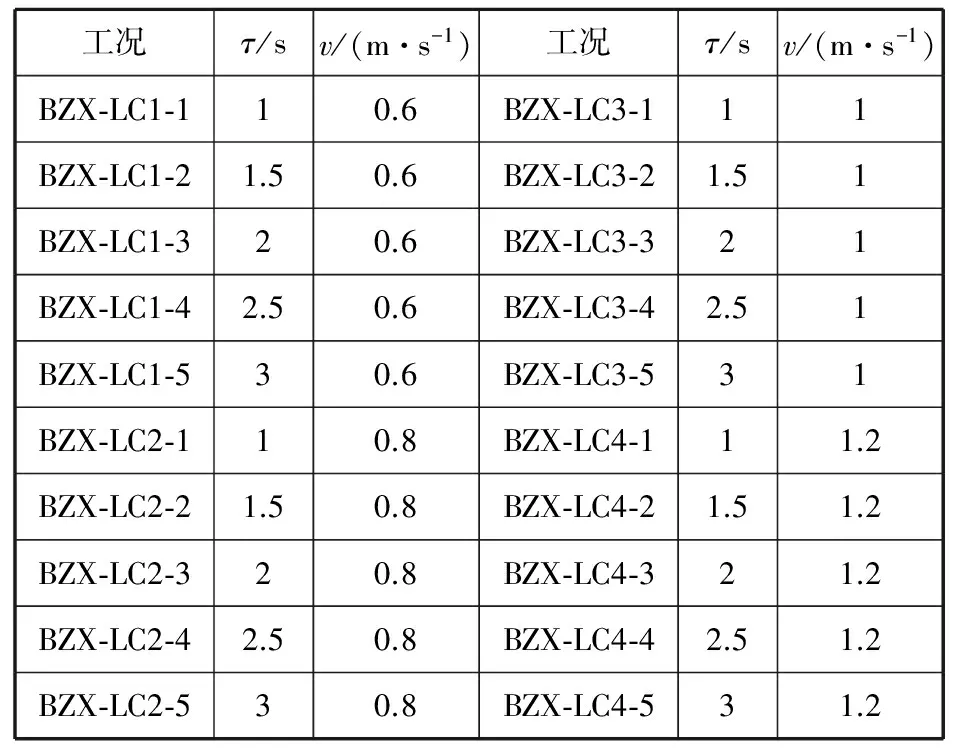
表1 半正弦加速曲线下结构的分析工况
除了上层建筑吊装前的重力载荷及居装件重量外,根据吊装方式及工况的不同,在吊点处施加不同的速度函数。图3为对应于起吊加速时间为1 s时不同恒定吊装速度下的速度-时间曲线,即v-τ曲线。
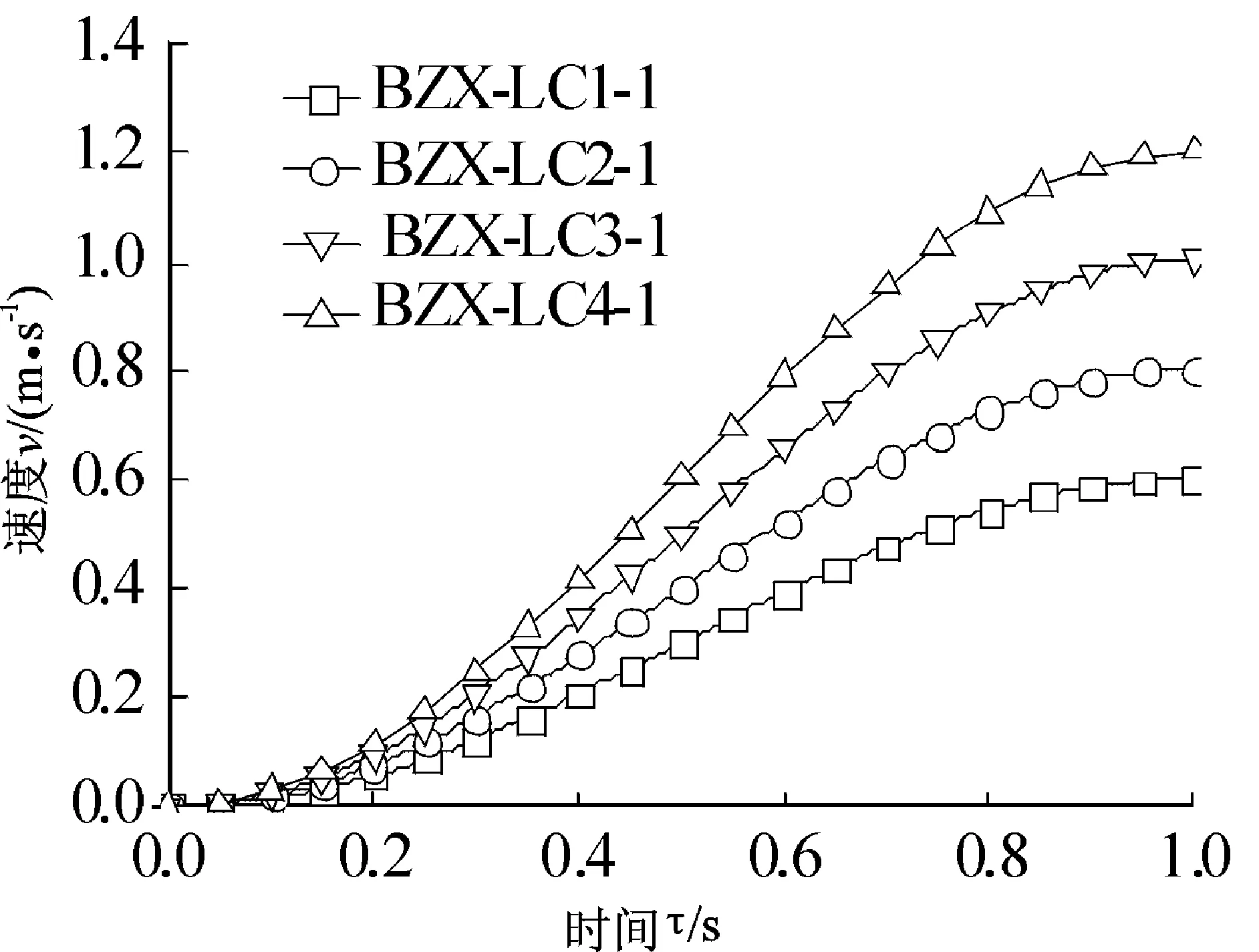
图3 几种不同工况下的速度曲线图
采用MD/Nastran软件进行瞬态分析,结果如图4~图5所示,可以得出:
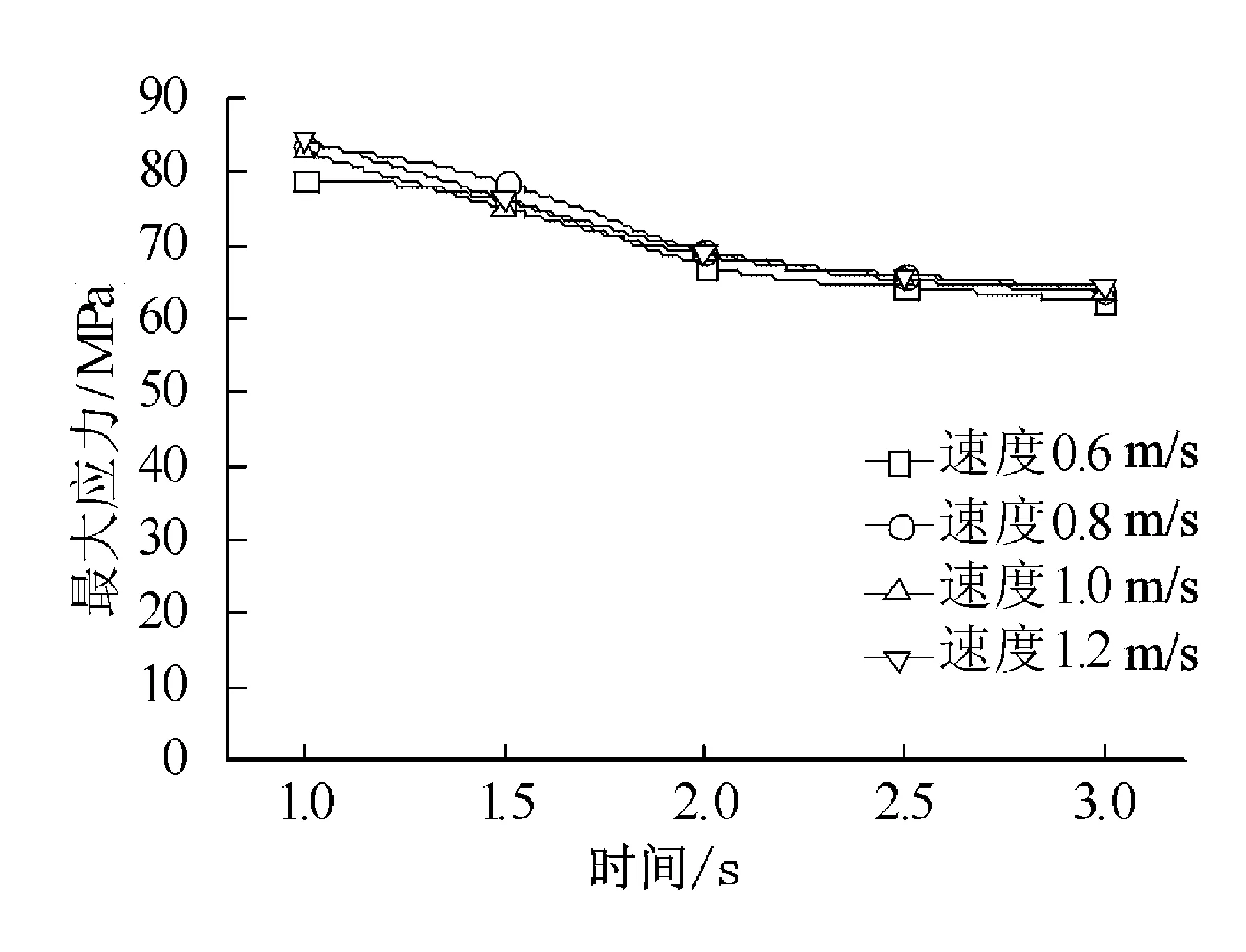
图4 结构应力随时间变化曲线
在起吊加速时间为1~2 s时,上层建筑结构的应力随时间降低的幅度大于起吊加速时间为2~3 s的情况。可见,增加起吊加速时间τ可以减轻冲击载荷对上层建筑结构的冲击,但过长的加速时间对降低上层建筑应力值效果并不十分显著;同一起吊加速时间下,速度越小,上层建筑结构应力值越小,但降低幅度较小,恒定吊装速度对上层建筑结构应力的影响程度小于起吊加速时间对其的影响。
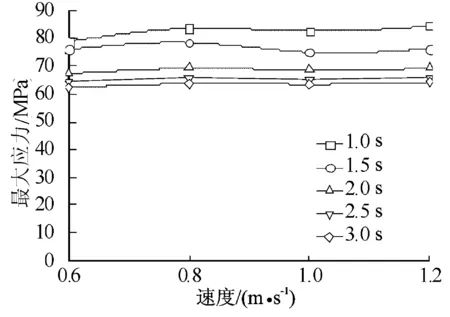
图5 结构应力随吊装速度变化曲线
图6为龙门吊吊装方式下,起吊加速时间3 s时,工况BZX-LC1下结构的应力云图。
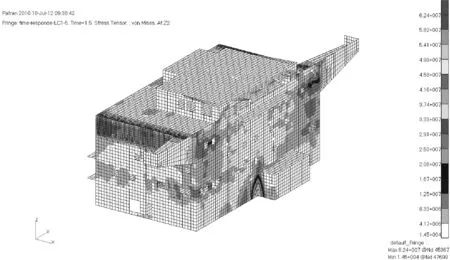
图6 工况BZX-LC1下上层建筑应力云图
对于起升电机采用其他3种加速曲线的情况,同样选择上节采用的20种工况进行分析,结果与半正弦加载曲线的结果类似。可知:不同加速曲线的不同工况中,起吊加速时间为3 s,恒定吊装速度为0.6 m/s时,对应于工况LC1-5下,结构所受到的冲击作用最小。
3 平稳吊装过程中上层建筑吊装强度
上层建筑起吊至离地300 mm距离后,将作仔细检查,确认无误后进行正式吊运。在正式吊装过程中,结构处于静力平衡状态。
由于上层建筑吊装过程中,结构在不断运动,处于“全自由”状态,但是对它进行有限元静力分析时,不能处理为全自由结构。惯性释放是MD/Nastran中的一个高级应用,允许对完全无约束的结构进行静力分析,简单地说就是用结构的惯性力来平衡外力。尽管结构没有约束,分析时仍假设其处于一种“静态”的平衡状态。采用惯性释放功能进行静力分析时,只需要对1个节点进行6个自由度的约束(虚支座)[8]。约束点可以由软件自行选择,也可以人工选择,2种方法得出的应力结果完全相同。
对上层建筑吊装过程中结构应力可采用惯性释放技术进行分析。
惯性载荷在型深方向取az=g=9.8 m/s2,其余方向为0。吊孔位置受到缆绳向上的拉力,大小与结构的自重相等。将建好的有限元模型调入MD/Nastran计算,上层建筑吊装过程中结构的最大应力与变形汇总见表2。
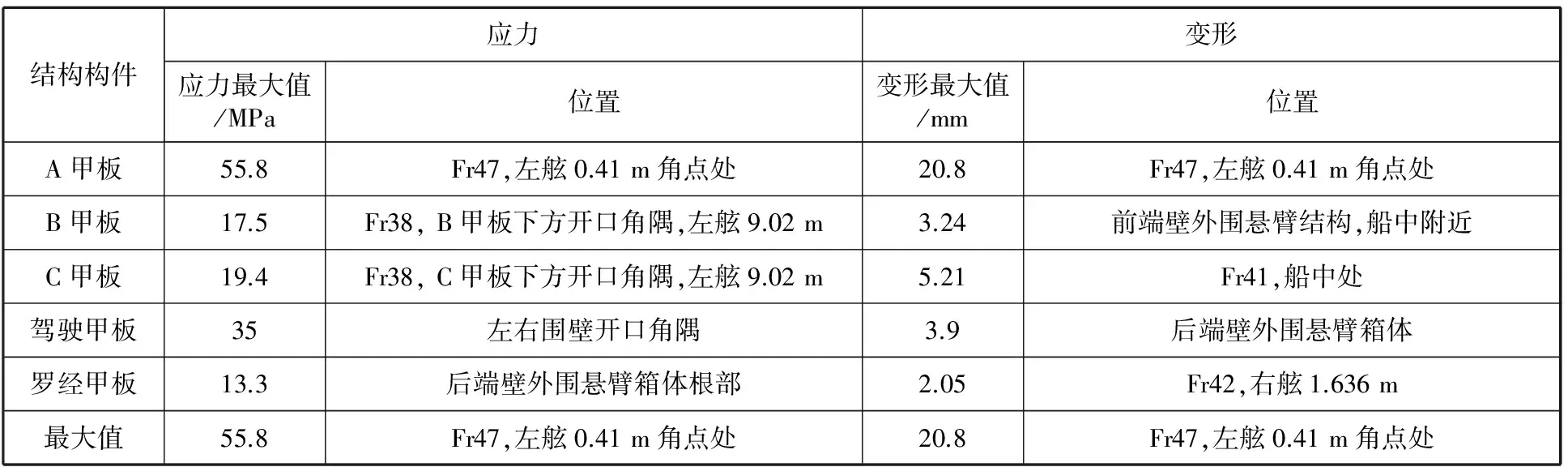
表2 上层建筑吊装过程中结构的最大应力与变形
图7为龙门吊吊装方式下,上层建筑结构在吊装过程中的应力分布图。
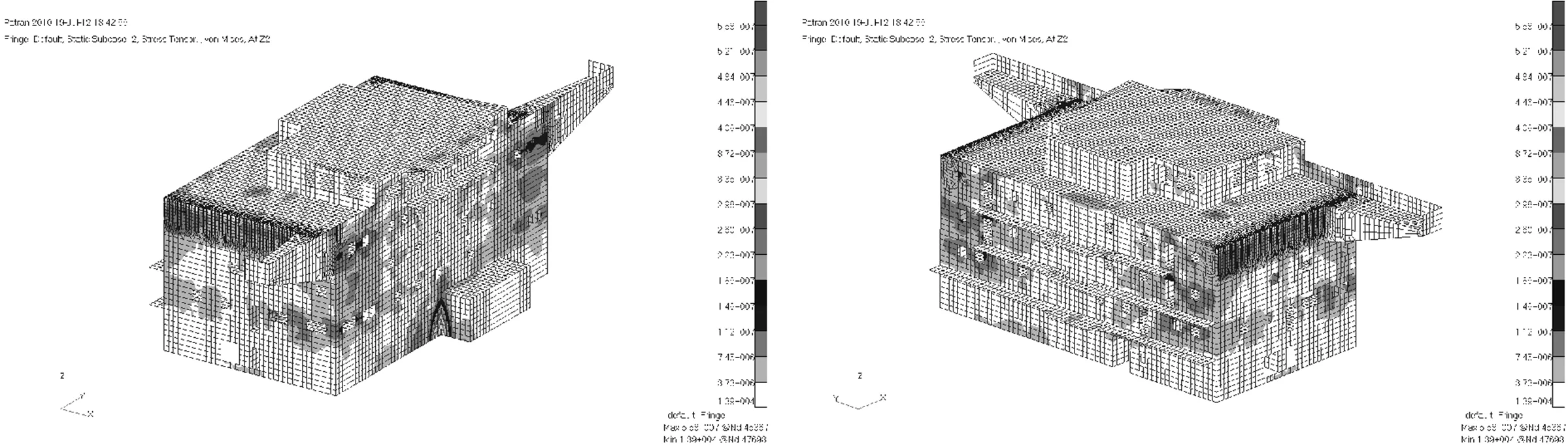
图7 吊装过程中上层建筑整体结构应力云图
4 吊装工艺中安全系数可靠性验证
根据起吊瞬间及平稳吊装过程中2个阶段上层建筑结构应力的分析,可以分别得到2个阶段上层建筑结构应力的最大值。根据起吊瞬间的冲击载荷对结构应力的影响,确定若采用静力计算替代瞬态分析,应该选择多大的安全系数,并判断目前上层建筑吊装有限元分析中安全系数的选取是否合理,结果见表3。
安全系数由起吊瞬间的最大应力值除以平稳吊装过程中的最大应力值得到。这里起吊瞬间不同起升电机加速曲线下,上层建筑结构的应力值为起吊加速时间取3 s,恒定吊装速度取0.6 m/s(对应工况LC1-5),以及起吊加速时间取1 s,恒定吊装速度取1.2 m/s(对应工况LC4-1)情况下的应力值,分别对应各种起升电机加速曲线下,上层建筑结构应力的最小值和最大值,其他工况下上层建筑的应力值介于两者之间。
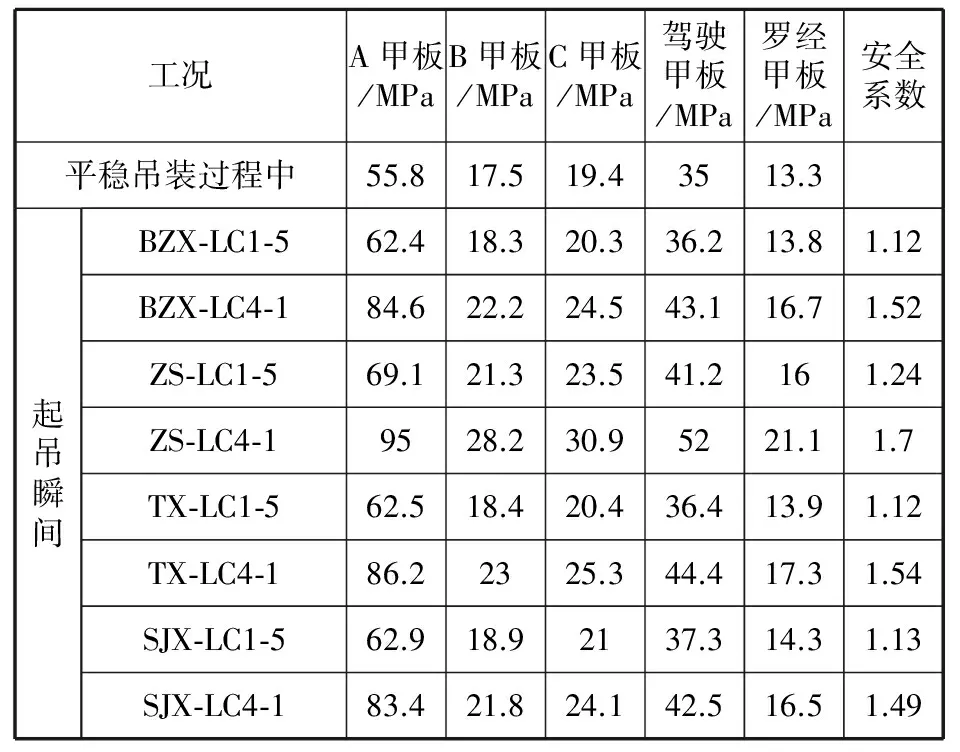
表3 上层建筑吊装工艺安全系数可靠性验证
由表3可以看出:
(1) 2种不同的吊装方式下,起升电机为正矢加速曲线,起吊加速时间取1 s,恒定吊装速度取1.2 m/s时,结构需要选取的安全系数最大。
(2) 半正弦加速曲线、梯形加速曲线及三角形加速曲线情况下,结构选取的安全系数相差不大。
目前,上层建筑吊装过程中选用的安全系数为1.1或1.2,可以看出这样的安全系数值在起吊加速时间长,吊装速度小的情况下准确性很高。
5 结论
本文以105 000 DWT油船上层建筑为例,采用MSC/Patran及MD/Nastran软件对上层建筑吊装过程进行动态模拟,起吊瞬间考虑了4种不同的加速度曲线,并根据起吊加速时间以及恒定吊装速度的不同设置了20种组合工况,得出了上层建筑起吊瞬态过程中,较为合理的起吊加速时间和恒定吊装速度。根据起吊瞬态过程与平稳吊装过程中上层建筑最大应力值的对比,判断现有上层建筑安全系数的合理性。结论如下:
(1)不论采用何种起升电机加速曲线,起吊加速时间愈长,恒定吊装速度越小,冲击载荷对上层建筑应力值的影响愈小。恒定吊装速度v对上层建筑结构应力的影响程度小于起吊加速时间τ对其应力的影响。在实际吊装过程中,选择较小的吊装速度及较长的起吊加速时间,可以有效地降低上层建筑结构应力。
(2)结合船厂吊装的实际速度与时间,上层建筑吊装过程中选用的安全系数为1.1或1.2,具有较高的准确性。
[1]中国船级社.船体结构强度直接计算指南[M].北京:人民交通出版社,2001.
[2]杨剑, 张璞, 陈火红.新编MD /Nastran有限元实例教程[M]. 北京: 机械工业出版社,2008.
[3]黄海燕, 刘晓卫.集装箱船结构动力学分析[J]. 船海工程, 2011,40(2):22-24.
[4]何成忠,胡吉全,王新华.带斗门座起重机在卸载冲击载荷下的动态特性研究[J]. 港口装卸, 2010(2):20-22.
[5]汤秀丽, 李和平.固定式起重机的支撑圆筒在地震载荷下的动态特性研究[J]. 港口装卸, 2009(1):10-11.
[6]王贡献,沈荣瀛.起重机臂架在起升冲击载荷作用下动态特性研究[J]. 机械强度, 2005,27(5):561-566.
[7]赵爽,等.抓斗起重机主梁动特性有限元分析[J]. 煤矿机械, 2011,32(9):79-80.
[8]张少雄, 杨永谦.船体结构强度直接计算中惯性释放的应用[J]. 中国舰船研究, 2006(1):58-61.
2014-06-17
程玉芹(1988-),女,助教,硕士研究生,主要研究方向为船舶与海洋结构物强度分析。
U661.43
A

