齿轮图的邻点强可区别的全染色

张东翰，李 超

(商洛学院数学与计算机应用学院，726000，陕西，商洛)

齿轮图的邻点强可区别的全染色

张东翰，李 超

(商洛学院数学与计算机应用学院，726000，陕西，商洛)

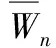
齿轮图；邻点强可区别的全染色；邻点强可区别的全色数

0 引言

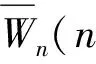
1 预备知识

定义1[7]：设G(V,E)是阶数不小于3的简单连通图，k是自然数，f是从V(G)∪E(G)到{1,2…k}的映射，如果满足：

1)对任意的边uv∈E(G),f(u)≠f(v),f(u)≠f(uv)≠f(v)；

2)对任意的两相邻的边uv,uw∈E(G)(v≠w),f(uv)≠f(uw)；

3)对任意的边uv∈E(G)，其端点的色集合满足C(u)≠C(v)，其中任一顶点u的色集合为C(u)={f(u)}∪{f(v)|uv∈E(G)}∪{f(uv)|uv∈E(G)}。

则称f是图G的一个邻点强可区别的全染色法(简记作k-AVSDTC)，且称数χast(G)=min{k|G存在k-AVSDTC}为G的邻点强可区别的全色数。

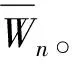
引理1[7]：设图G是阶数不小于3的图，有χast(G)≥△+1；若G有相邻的2个最大度点，则有χast(G)≥△+2，其中△代表图G的最大度。

本文中未加叙述的术语、记号可在文献[9-11]中找到。

2 定理及其证明

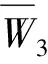
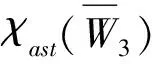
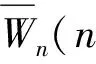
综上可知，定理2成立。

[1]Zhang Zhongfu,Zhang Jianxun,Wang Jianfang,The total chromatic number of some graphs[J].Science Sinica Ser A:1434-1441.

[2]张东翰.蛛形图的全染色和星全染色[J].商洛学院学报,2013,27(6):31-32.

[3]李晓东.图全染色的几个定理[J].哈尔滨理工大学学报,2001,6(1):100-102.

[4]张忠辅,陈祥恩,李敬文,等.关于图的邻点可区别的全染色[J].中国科学:A辑,2004,35(5):574-583.

[5]张东翰,王晓.路的广义Mycielski图的邻点可区别的全染色[J].兰州理工大学学报,2009,35(5):146-147.

[6]陈祥恩,张忠辅.Pm∨Pn的邻点可区别的全染色[J].西北师范大学学报,2005,41(1):13-15.

[7]张忠辅,程辉,姚兵.图的邻点强可区别的全染色[J].中国科学:A辑,2007,37(9):1073-1082.

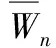
[9]张东翰,朱白.路的D(3)-点可区别的全染色[J].商

洛学院学报,2014,28(2):11-12.

[10]Bondy J A,Murty U S R.Graph Theory with Applications[M].New York:The Macmillan Press Ltd,1976.

[11]Reinhard D.Graph Theory[M].New York:Springer-Verlag,1997.

TheAdjacent-Vertex-Strongly-DistinguishingTotalColouringoftheGearGraph

ZHANG Donghan,LI Chao

(College of Mathematics and Computer Applications,Shangluo University,726000,Shangluo,Shanxi,PRC)

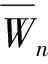
the gear graph;the adjacent vertex strongly distinguishing total colouring;the adjacent vertex strongly distinguishing total chromatic number

2014-05-21;

2014-06-23

张东翰(1981-)，男，河北邢台人，硕士，讲师，研究方向：图论及其应用。

陕西省自然科学基础研究计划项目(2013JM1023)；陕西普通本科高等学校教学改革研究重点资助项目(13BZ56)；陕西省教育厅科研计划基金项目(14JK1225)；商洛学院教育教学改革研究项目(14JYJX133)。

10.13990/j.issn1001-3679.2014.04.015

O157.5

A

1001-3679(2014)04-0493-03